对一道统测试题的探源及拓展*
●陈 儿 (奉化中学 浙江奉化 315500) ●杨亢尔 (武岭中学 浙江奉化 315502)
对一道统测试题的探源及拓展*
●陈 儿 (奉化中学 浙江奉化 315500) ●杨亢尔 (武岭中学 浙江奉化 315502)
文章通过对一道2015年1月浙江省杭州市高三(理)统测试题的探源和拓展,追根溯源回归到圆的性质,开拓出解决椭圆问题的新思路,揭示了圆锥曲线的内在联系,促进了数学知识的融会贯通.
探源;拓展;统一;相似性
1 试题呈现

1)求点C的轨迹Γ的方程.


第2)小题的解法如下:

图1
解法1 设点E,F,K的横坐标为x1,x2,x3,点D(x0,y0),直线m的方程
y=kx+b,
则切点弦PQ的方程为
计算得
将直线m代入椭圆方程,得


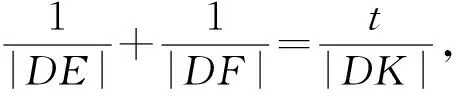
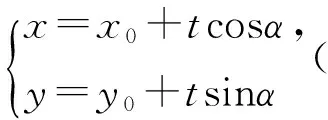

将直线m的参数方程代入椭圆方程,得

求得t=2.
2 试题探源
弄清楚试题的源头,有助于把握问题的来龙去脉.本题研究的是圆锥曲线中直线与椭圆的位置关系,而椭圆与圆可经过伸缩变换相互转化且对应图形的位置关系保持不变.因此,可尝试将椭圆转化成圆,容易证明如下命题成立.

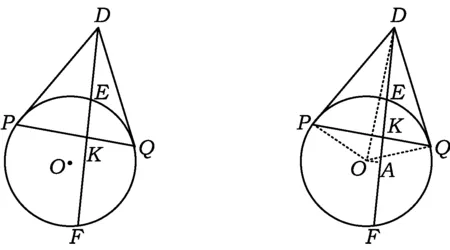
图2 图3
证明 如图3,取EF的中点A,由垂径定理得OA⊥EF.因为DP,DQ是切线,所以
∠DAP=∠DQP.
又因为DP,DQ是切线,所以
∠DPQ=∠DQP,
从而
∠DAP=∠DPK,
于是
△DAP∽△DPK,
故
|DP|2=|DK|·|DA|.
由切割线定理得
|DP|2=|DE|·|DF|,
从而
|DK|·|DA|=|DE|·|DF|.
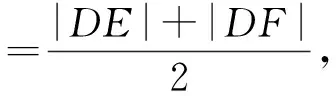


3 试题拓展
因为椭圆、双曲线、抛物线是可以统一定义的,所以它们具有许多统一的性质.类比椭圆,可得到如下圆锥曲线的统一性质:

图4

如图4,以抛物线y2=2px(其中p>0)为例加以证明:
证明 设点D(x0,y0),则直线m的参数方程为
其中t是参数.若点E,F,K的参数为t1,t2,t3,则

将直线m的参数方程代入抛物线方程,得
t2sin2α+(2y0sinα-2pcosα)t+y0-2px0=0,
从而
设点P(x1,y1),则直线DP的方程为
又点D在直线DP上,从而
即
px1-y0y1+px0=0.
同理可得
px2-y0y2+px0=0,
因此直线PQ的方程为
px-y0y+px0=0,
将直线m的参数方程代入PQ的方程得
求得t=2,结论成立.
进一步探究:既然椭圆与圆有很多相似性,猜想上述性质的逆命题在圆中是否成立?得到如下性质:
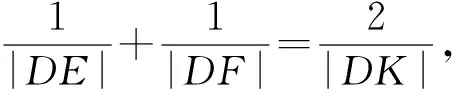
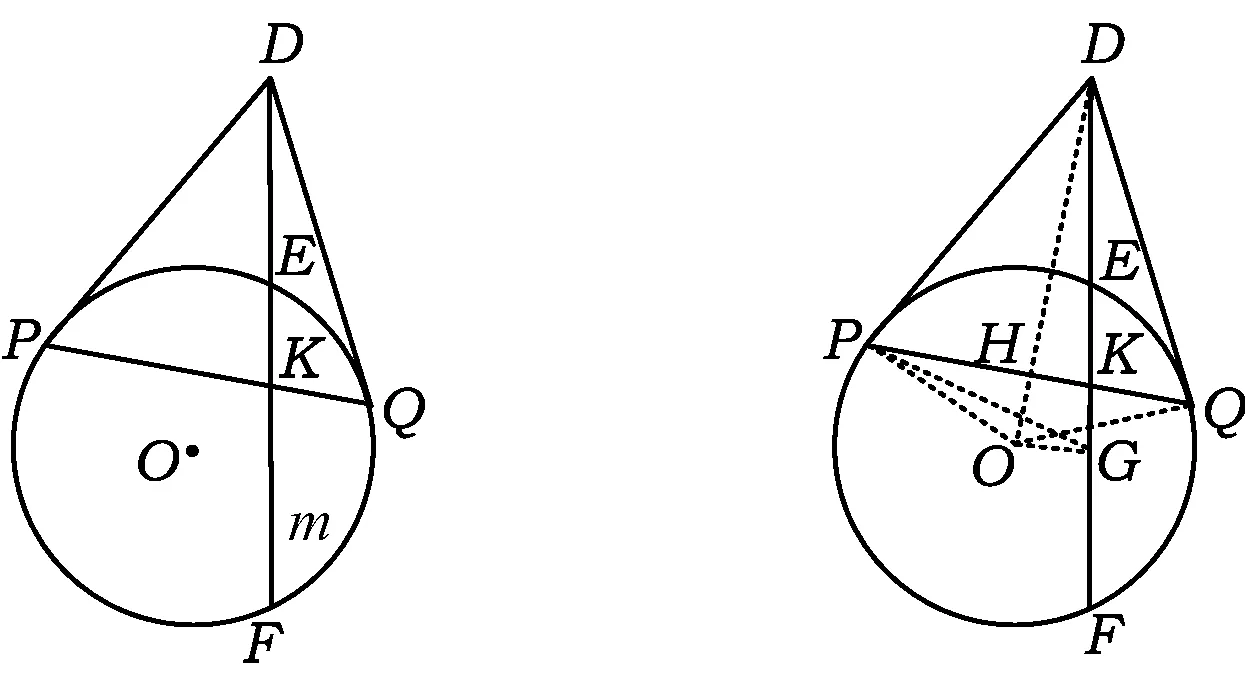
图5 图6
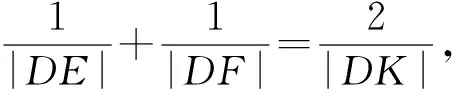
DG·DK=DE·DF.
因为DP与⊙O相切于点P,所以
DP2=DE·DF,
从而
DP2=DK·DG.
又∠KDP=∠PDG,从而
△KDP∽△PDG,
于是
∠DGP=∠DPK.
因为∠DPO=∠DGO=90°,所以点P,D,G,O共圆,从而
∠DGP=∠DOP,
于是
∠DOP=∠DPK,
故
DO⊥PQ,
进一步得
△DPO≌△DQO,
从而
∠DQO=∠DPO=90°.
继续拓展,上述性质在椭圆中成立吗?
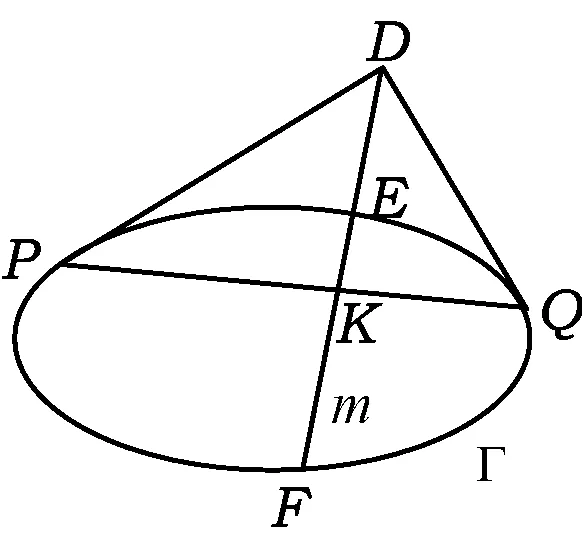
图7

(证明略.)
至此,通过对这道统测题的探源和拓展,揭示了圆锥曲线的内在统一性,显示了数学知识之间的纵横联系,促进了数学知识的融会贯通.有了这样的认识,我们的探究不再孤立,学生的思维能力得到了明显提高,同时也彰显了数学的核心价值.
2016-11-24;
2016-12-30
陈 儿(1978-),女,浙江奉化人,中学高级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)04-17-03

