引导高中生提高数学运算能力的基本方法

黄行铭

（福州市屏东中学，福建 福州 350000）

引导高中生提高数学运算能力的基本方法

黄行铭

（福州市屏东中学，福建 福州 350000）

针对目前高考数学对学生运算能力的要求和当前高中生运算能力的现状，提出培养高中生数学运算能力的若干基本方法。

高中数学；运算能力

自福建省中考允许使用计算器以来，许多初中学生忽视了对运算能力的自我训练与培养，但由于在高中学习阶段数学考试中不允许使用计算器，于是，这些学生在考试的运算问题中就会经常发生错误，致使学习成绩明显退步，逐渐对数学学习失去信心，失去兴趣。

数学高考虽不要求考生具备进行十分复杂运算的能力，但要求学生在不使用计算器的情况下有较熟练的基本运算能力。考生具备了较熟练的基本运算能力，才能在规定的考试时间内迅速而又正确地完成答题，才能获得数学高考的大部分基础分数，这也是考生在数学高考中能取得好成绩的必要前提。

“准确”是运算的最基本要求，正确地记忆和运用公式及法则，是准确的前提，是运算能力的第一层次要求，学会采用合理与简捷的方式，对应用公式与法则时做到能正用、逆用、变用和活用，这是对高中学生运算能力的第二层次要求。运算能力的培养、训练并不是枯燥乏味的机械重复，它需要动员学生用“眼”，用“心”，用“脑”，寻找最佳的运算途径，使之能从中体验到运算的乐趣。在实际教学中我们可以引导学生从以下几个方面着手以提高数学运算能力。

一、熟记数学公式与常用数据

培养学生的运算能力，除了要让学生熟记数学公式之外，还要让学生熟记一些常用的数据与公式、法则，甚至要掌握一些口算、速算的方法。如：1～21的平方数；2n(n=1、2····10）的值；lg5的值；特殊的勾股数3、4、5；5、12、13；7、24、25；8、15、17；9、40、41等；许多特殊的三角函数值；等边三角形的面积与边长的关系等。让学生熟记这些数据，才能提高学生的解题运算速度。运算能力也是在日常学习中逐步积累起来的，日常教学中，教师应针对许多常用的公式与数据，提醒学生有意识地加强记忆与训练。

二、运用数形结合思想简化运算过程

高中数学的学习大都是围绕着数与形进行的，数形结合的思想是数学学习中必须掌握的一个重要的思想。所谓数形结合，是指通过以形助数，或以数解形，使抽象问题直观化、复杂问题简单化的一种思维方法.使用数形结合方法，常可使许多貌似复杂的运算问题迎刃而解。“数”与“形”之间有着密切的联系，“数”可以用“形”直观的表示出来，“形”可以用“数”来准确的研究，在解题时，促使数与形的完美结合，往往是选择解题思路时的最佳途径。因此，培养高中学生的运算能力，要让学生学会借助图形进行精简的计算和推理，直观、准确地得出正确的答案，这也是每位高中学生必须掌握的基本方法，在日常教学中，教师要在一些例习题的训练中强化这种数形结合的意识，使学生体会到：“数与形本是相倚依，焉能分作两边飞；数缺形时少直觉，形少数时难入微；数形结合百般好，隔裂分家万事休；几何代数统一体,永远联系莫分离”。

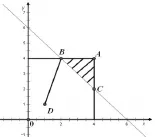
分析：如图，在直角坐标中，做出可行域△ABC，的各顶点坐标分别是A(4,4)、B(4,2)、C (4,2)，则表示可行域△ABC内任意一点（x,y）与定点(1,1)的连线斜率。观察图形可知，当动点移到可行域内的点B时，Z取得最大值

这是一个已司空见惯的线性规划小问题，但在教学中，师生都较少去体会在问题中数形间的紧密联系，品味问题解决过程中的数形结合思想，漏失了一次强化数形结合意识的良机。

例2.已知 x,y,z∈R且2x+3y+3z=1，则 x2+y2+z2的最小值为 。

分析：大多数学生解这一道题会使用柯西不等式，但是，如果将x2+y2+z2改写为(x-0)2+(y-0)2+(z-0)2，则问题可转化为求原点（0,0,0）到平面2x+3y+3z-1=0中的距离d的平方数最小值，联想到点到直线的距离公式，类比可得故有x2+y2+z2的最小值是

这个问题的以上解法需要学生具有较强的数形结合思想意识，并能通过类比与联想对问题进行猜想，才能迅速获得结论。

三、从定义出发探求解题途径，学会灵活运算

《考试说明》对高中学生的运算能力提出了如下要求：会根据概念公式和法则，对数、式和方程进行正确的运算和变形。数学定义是几千年来社会实践的必然结果，也是定理、性质、推论、公式的根本所在。定义反应的是事物的本质属性，解题时经常追根溯源，从概念的定义出发探求解题途径，往往是最直接、最有效的方法，可以避开许多不必要的运算。

例3.已知函数 f(x)= ||x-a，

（1）若不等式 f(x)≤3的解集为{|x-1≤x≤ }5，求实数a的值；

（2）在（1）的条件下，若 f(x)+f(x+5)〉m对于一切实数x恒成立，求实数m的取值范围。

分析：在正常情况下，大多数考生通过分区间求分段函数，根据图像可以得出正确的解题思路。如考虑用绝对值的定义： ||x表示数x表示的点到原点的距离， ||x-a≤3表示数x在数轴上表示的点到数a表示的点的距离不超过3的解集为：1≤x≤5，则数a表示的点就是数-1表示的点与数5表示的点的线段中点所表示的数易得a=2。（2）中表示的是：f(x)+f(x+5)= |x-2|+ |x+3|中表示的是：数x表示的点到数2与数-3表示的点的距离之和。根据两点间线段最短，可知数2到数-3的距离为5，可知|x-2|+ |x+3|〉5 ，根 据 题 意 要 求 ，x∈R 时 ，f(x)+f(x+5)≥m恒成立，故m≤5。

《考试说明》同时要求高中生能分析条件，寻找合理、简捷的运算途径，也就是要求学生不仅要具备基本的运算能力，还要能正确、迅速、合理的完成运算。要想正确、迅速、合理的完成运算，必须加强“运算灵活性”的培养，它可以有效合理地利用有限的时间和精力，减少运算的步骤，降低运算错误的概率。

例4.若对于实数x，有x3=a0+a1(x-2)+a2(x-2)2+a2(x-2)3，则a2的值为( )

A.3 B.6 C.9 D.12

分析：从已知条件中可以看出等式右边等式的二项展开式中含有因式x-2，左边的有x3，此时如能把x看作(x-2)+2，则有[( x-2)+2]3=[2 +(x-2)]3，a2是展开式中第三项(x-2)2的系数c32×2=6。

四、合理运用估算，规避繁琐运算过程

《考试说明》要求高中生能分析条件，寻找合理、简捷的运算途径，能根据要求对数据进行估算，并能进行近似计算。估算是在日常生活中必不可少的一项基本技能，良好的估算能力可以让学生做到“心中有数”，同时也是提高运算能力的很好的帮手。利用具体条件和有关知识对事物的数量或算式的结果，作出的大致推断或估计。正确的估算会对迅速解题，正确判断运算结果带来必要的灵活性和机动性。

当 x=1时，y1=e，y2=1，此时，y1〉y2。

数学学习需要学生有明确的学习动机、浓厚的学习兴趣与充足的学习信心，日常教学中，教师应主动了解学生学习的心理现状，积极研究对策，弥补学生因运算能力不足造成的学习信心不足等心理问题。事实上，加强对学生意志品质的磨炼，提升学习数学的自信心，使之养成永不放弃的性格，对提高学生的运算能力也有重要作用。

［1］马萍.浅谈如何培养学生的运算能力［J］.数学学习与研究，2013(4).

［2］张倩.如何培养学生的运算能力［J］.考试周刊，2012(27).

［3］柏宗玲.如何培养学生的数学基本能力［J］.学周刊，2011 (17).

（责任编辑：王钦敏）