方形数阵的求和运算及其应用

余明芳 王钦敏

（福建教育学院数学教研室，福建 福州 350025）

方形数阵的求和运算及其应用

余明芳 王钦敏

（福建教育学院数学教研室，福建 福州 350025）

将方形数阵看作是数列在二维形式上的一种推广，可以按某种方式归纳出许多方形数阵的数字变化规律，给出它们的通项与求和运算方式，并将其应用于一些数列求和问题中。方形数阵求和运算及其应用问题，是数列问题的自然延伸，是数列章节开展探究式教学的良好素材。

方形数阵；求和运算；自然数等幂和

一个数列中的数，不仅具有次序，而且大都具有一定的变化规律，我们可归纳其变化规律获得许多数列的通项与求和公式。在各种图式的数阵中，正方形图式的数阵最为常见，笔者发现，如果将方形数阵看作是数列在二维形式上的一种推广，也可以归纳许多方形数阵的变化规律，求出其通项与所有项之和的公式，并应用于一些数列求和问题中。

一、方形数阵的求和运算

在如下所示的n阶方形数阵中，记其第m行第n列的数为通项amn，接着按数阵中标示的线路，分别记A1=a11，A2=a21+a22+a12，A3=a31+a32+a33+a23+a13，…，Am=am1+am2+…+amm+…+a2m+a1m，则方形数阵所有项之和S=A1+A2+A3+…+An，据此可将求方形数阵所有项之和问题转化为数列的求和问题，对一些已知通项amn的方形数阵进行求和运算。

1.对通项为amn=mn(m,n∈Z+)的方形数阵，Am=am1+am2+…+amm+…+a2m+a1m=m+2m+3m+…+m2+(m -1)m+…+2m+m =m3，故

2.对通项为amn=a+(m-1)d+(n-1)r(m,n∈Z+)的方形数阵，

当a=2，d=r=1时，通项为amn=m+n(m,n∈Z+)，S=n3+n2。

3.对通项为 amn=apm-1qn-1(m,n∈Z+)的方形数阵，所以

二、方形数阵求和运算方式的应用

我们可以构造一个方形数阵，利用上述求方形数阵所有项之和的运算方式，求出数列｛n2｝、｛n3｝的前n项和。

教师在采用任务驱动教学法教学时，需重视学生的主体地位。因而，教师在设置实训课程时，需将实训内容包含在每个实训任务当中。教师需指导学生自主发现、思考、解决问题，学生在完成实训任务之后，教师需及时进行总结，并鼓励学生发现问题、解决问题。教师在设置实训任务时，需重视培养学生自主学习能力及思维能力，为学生日后的学习及发展奠定坚实基础。教师在教学过程中，需重视对学习方法的讲解。教师在设置车工实训任务时，需重视实训任务的层次性。由于每个学生的理解能力、综合素质水平不同，因此教师在设置实训任务时，需重视任务的有效性，做到因材施教，以保证教学效果。教师需指导学生自主分析、解决问题。

由12+22+32+…+n2=1+(1+2+1)+(1+2+3+2+1) +…+[1+2+3+…+n+(n-1)+…+2+1]与13+23+33+…+n3=12×1+22×2+32×3+…+n2×n =1+(1+2+1)2+(1+2+3+2+1)3+…+[1+2+3+…+n +(n-1)+…+2+1]n，易归纳并证得S=1k+2+2k+2+3k+2+…+nk+2=1k+22×2k+32×3k+…+n2×nk1k+(1+2+1)2k+(1+2+3+2+1)3k+…+[1+2+3+…+n +(n-1)+…+2+1]nk。

因而可构造数阵

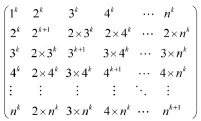
不难发现，这个数阵与自然数等幂和问题有密切联系，不妨称其为自然数幂和数阵。我们可以利用这个数阵给出前n个自然数平方和公式与立方和公式的直观模型。

1.当k=0时，数阵为

数阵所有项之和为S=12+22+32+…+n2。若将数阵中的所有项按数阵中新给出的线路相加，又可得所

换一个角度看，将数阵左下部分逐行相加，再将右上部分逐列相加，数阵中所有项的和

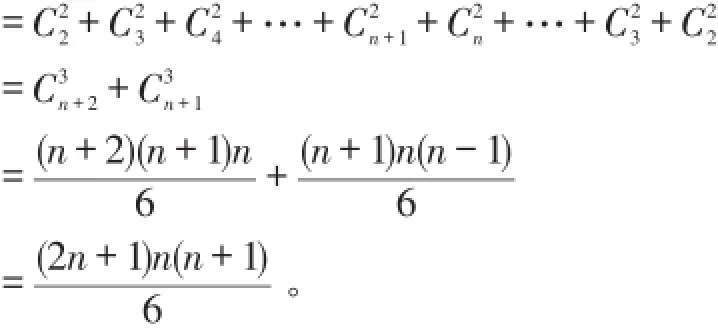
从以上过程可见，自然数幂和数阵在数列求和问题中有独特作用。

2.当k=1时，数阵为

这时，数阵所有项之和为S=13+23+33+…+n3。

通过观察可以发现这个数阵的各行各列均为等差

数列，其通项为aij=ij，所有项之和

换个角度观察数阵，易看出数阵的第k列的n个数之和是第1列的n个数之和的k倍，故所有项的和应为第1列的n个数之和的倍，从而可以直观地看出等式成立。

方形数阵的求和运算及其应用问题，是数列问题的自然延伸，在数列章节教学中，将这些内容作为探究式教学素材，可以帮助学生拓宽认知视野，提高学习兴趣，从更高层面理解数列的概念与相关知识间的关系。

［1］王钦敏.教材边上好数学［M］.福州：福建人民出版社，2014.

［2］王钦敏.如何对数学教材进行有益的拓展与改造［J］.数学通报，2013(1).

［3］余明芳，王钦敏.例谈高中数学探究性课题的选择与教学设计［J］.数学通报，2015(11).

（责任编辑：万丙晟）

福建省教育科学“十三五”规划2016年度重点课题“中学生发现数学问题能力的培养研究”（项目编号：FJJKCGZ16-177）。