数学思想方法在高中数学教学实践中的应用

游明霞

（福安第一中学，福建 宁德 355000）

数学思想方法在高中数学教学实践中的应用

游明霞

（福安第一中学，福建 宁德 355000）

数学思想是数学知识学习的核心，要素在教学中，教师应深入研究教材，仔细发掘蕴藏其中的数学思想方法，以数学思想方法引领教学，使学生深刻把握知识在教学整体结构中的内在联系；从数学思想的角度指导解题教学，提高学生的思维水平和创新意识；不断引导学生感悟数学的思想方法，提升学生的数学素养。

数学思想方法；函数与方程思想方法；数学素养；数学教学

通常，许多人都误以为学数学是为了解题、考试，学数学就是学数学公式、数学定理等数学知识，而这些数学知识在他们走出校园，走上社会后，会渐渐淡忘，也就产生了数学无用论的观念。其实这种观点忽视了长期的数学学习给我们留下的铭刻在头脑中的数学思想、数学思维方法以及看问题的着眼点，而这些却随时随地影响人们的工作、生活等行为方式，让人们受益匪浅！

每门学科背后都是一种思维方式，这种思维方式比学科知识本身更重要。其之用，是无用之用，实有大用。日本数学教育家米山国藏先生指出：科学工作者所需要的数学知识，相对地说是不多的，而数学的精神、思想与方法却是绝对必要的。数学的知识可以记忆一时，但数学的精神、思想和方法却随时随地发挥作用，可以使人受益终身。但是，受以传授知识为目标的教学观念和模式的长期影响，加上高中数学知识点繁、杂、多的特性，教师往往把重点放在知识的讲解上，在习题教学中也大部分以题论题，忽视知识发生发展的过程，重结论轻过程，不重视数学思想方法的教学。如何才能更好地在高中数学课堂中落实思想方法的教学呢？笔者在教学实践中总结了以下几个途径，不当之处，敬请指正。

一、以数学思想方法引领教学，使学生深刻把握知识在教学整体结构中的内在联系

数学思想属于数学知识学习的关键性因素，是对数学概念与知识的一种总结与概括，也是对数学本质的一种认识。但在教科书中数学概念与知识是显性的，而数学思想方法通常是潜隐的学生在学习中很难自主发现数学概念与知识中隐藏的数学思想方法，需要教师深入研究教材，仔细挖掘出其中的数学思想方法并随渗透在教学的各个环节。例如，函数是高中知识的一个重要部分，也是学生学习的难点之一，其中，函数与方程思想是学习函数过程的核心内容，教师应该把函数与方程思想方法教学贯穿始终，逐步深化学生的理解与感悟。

例1.从方程ab=N（a＞0且a≠1）入手引出三个初等函数：

（1）当a固定，N随b的变化而变化就产生了指数函数y=ax；

（2）当a固定，b随N的变化而变化（ay=x）就产生了幂函数y=logax；

（3）当b固定，N随a的变化而变化就产生了幂函数y=xb。

例1中通过一个二元方程给学生总结指、对、幂三类初等函数解析式，揭示了方程与函数的本质联系，将方程静态的表达式看成动态的函数解析式，把握住了指、对、幂三类初等函数的内在联系，有助于学生整体把握教材。所以在教学中教师不仅要有利用数学思想方法反思教材的意识，还要有意识地培养学生利用数学思想方法随时反思的习惯。

二、从数学思想的角度指导解题教学，以提高学生的思维水平和创新意识

对师生而言，高中数学教学的一个重要目的是为了迎战高考，高考数学不仅考查数学基础知识和基本技能，更注重考查知识的内在联系，注重对中学数学中所蕴涵的数学思想方法的考查。而解题又是如今数学教学的一个重要方式，因此，在课堂教学中，教师应仔细挖掘蕴藏在习题中的数学思想方法，从数学思想的角度指导解题教学，可以更好地提高学生的思维水平和创新意识。

例2.已知mn≠0，n2+m＞0，又a≠b，且

ma2+na-1=0；① mb2+nb-1=0，②

试求过点 A(a2,a)、B(b2,b)两点的一次函数解析式（用含m、n的式子表示）。

解法一：设过点 A、B的一次函数解析式为y=kx+c，把A、B两点代入整理得

由 ①② 两式可知，a、b是一元二次方程mx2+nx-1=0的两实数根，根据韦达定理有

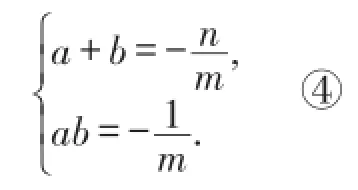
解法二：由①②方程可知，点A、B两点都是二元一次方程mx+ny-1=0的解，所以过点 A(a2,a)、B(b2,b)两点的一次函数解析式为mx+ny-1=0。

解法一由结论出发惯性思维想到用待定系数法设出直线方程，然后两点代入算出k,c关于a,b的表达式，最后根据③④式用韦达定理把含a,b的解析式转化为m,n的一次函数解析式，从而达到解题的目的。这种解法虽然也能得满分，但更多的表现为解题套路的操作和单纯的演算上，不仅计算量大、耗时间，而且容易算错。而解法二在函数与方程的思想方法的指导下，深刻理解“一次函数”与“二元一次方程”的内在联，秒杀了解题过程，从而提高了解题效率，有效地展示学生的思维水平和创造意识。因此，要提高解题的能力和水平，首先就要站在较高的观点上去研究解题，就是要从数学本质上去看待解题，就要在解题的规程中体现数学思想方法并注意发挥数学思想方法的功能。

三、不断引导学生感悟数学的思想方法，提升学生的数学素养

数学知识，会被渐渐淡忘，但对数学思想方法的领悟、理解能力，以及灵活、正确地用数学思想方法解决问题的能力，即数学素养将伴随人们一生，并在未来的生活和工作中发挥重要作用。

例3.微软公司招聘员工的一道考题：“一个屋里有50个人，每人带一条狗，其中部分是病狗。主人只能通过对其它狗的观察得知自己的狗是否是病狗，并在发现当天用枪打死自己的狗，第一天没有听到枪声，第二天没有听到枪声……直至第十天听到一片枪声，问屋里有多少病狗。”

可是这道看似脑筋急转弯的题目其实是一道巧妙的数学应用题。

答案分析如下：

若恰有1只病狗，则病狗主人在第一天就能发现其它49只狗都是正常的，则由此推断必然存在的病狗就是自己的狗，所以第一天就能听到枪声，结论：第一天听到枪声即等价于恰有1只病狗；

如果第一天没听到枪声，说明有2只或者两只以上的病狗，若病狗主人看到的病狗数大于等于2只的，则无法推断自己的狗是否生病，而病狗主人若只看到了1只病狗，则由此可以推断剩下的1只病狗就是自己的狗，所以第二天就应该听到枪声，结论：第二天听到枪声即等价于恰有两只病狗；

如果第二天没听到枪声，说明有3只或者3只以上的病狗，若病狗主人看到的病狗数大于等于3只的，则无法推断自己的狗是否生病，而病狗主人若只看到了1只病狗，则由此可以推断剩下的2只病狗就是自己的狗，所以第三天就应该听到枪声，结论：第三天听到枪声即等价于恰有2只病狗；

依此类推，前n-1天都没听到枪声，说明病狗数量大于或者等于n只，若病狗主人看到超过n-1只病狗，则无法推断自己的狗是否生病，只能继续等下去，而如果病狗主人只能看到n-1只病狗，即可推断剩下的一只病狗就是自己的狗，则在这一天就应该听到枪声，结论：在第n天听到枪声即等价于恰有n只病狗。

虽然整个解答过程没有用到任何数学定理、公式等数学知识，但需要结合运用反证法和归纳法这些数学思想方法，答案的揭晓使每个人都能感受到了数学的奥妙。有专家认为“良好的数学教育”的终极目标是提升学习者的数学素养，而数学素养形成的重要标志之一便是感悟和理解数学的思想，能够运用数学思想方法去处理数学领域内和领域外的问题。因此教师的教学应通过不断加强学生数学思想方法的训练，提高他们对数学的理解能力，从而从而提升他们的数学素养。

总而言之，在教学中渗透数学思想方法应该成为所有数学教师的共识。在教学工作中，数学教师要把渗透数学思想方法真正纳入到教学目标中，努力钻研教材，找准浅层的知识技能与深层的思想方法的结合点，有创造性地精心设置各个教学环节，自然渗透，让学生在学习知识和技能中理解数学、感悟数学思想方法，有效促进学生数学思维品质的提升，最终形成良好的数学素养，真正达到“教、学、用”合一的育人效果。

［1］张德新.在数学教学中渗透数学思想方法的意义及策略［J］.中学教学参考，2016(5).

［2］刘彩萍.高考数学中数学思想方法的研究及启示［D］.上海:上海师范大学，2010.

［3］李文欣.论数学思想方法与高中数学教学［J］.数学学习与研究，2011(3).

（责任编辑：王钦敏）

福建省教育科学规划课题“基于‘导学研讨训练拓展’模式下高中数学学案研究”（项目编号：FJJK15-548）。