从高等数学的思维模式看待高中数学

江苏省句容市实验高级中学 潘 龙 张 慧

从高等数学的思维模式看待高中数学

江苏省句容市实验高级中学 潘 龙 张 慧

本文研究了高等数学知识解决初等问题的必要性，举例说明了拉格朗日中值定理、函数凹凸性在高中解题中的应用。

高等数学；初等数学；拉格朗日中值定理；函数凹凸性

高等数学观点下的高中数学问题，是指与高等数学联系紧密的初等数学问题，或者是初等数学问题中含有高等数学的背景。近几年来随着课程改革的不断深入，含有高等数学背景的初等数学问题在历年各省的高考数学试卷中不断出现，中学数学中涉及高等数学的内容不断增加，可以说这是数学发展的必然。作为一名高三一线数学教师，如果在平时的日常教学中对某些问题忽视高等数学这一背景，单纯应用初等数学学科内容处理问题，势必会让学生感知到一定程度的“繁”、“难”、“偏”，打击学生学习的积极性，给实际的教学效果造成不良影响。但反之，若在高三的数学教学过程中加入高等数学的一些相关内容，不仅可以开阔学生视野，提高学生学习兴趣，同时教师也可以站在更高的视角，从高等数学的角度，以宽泛的视野来诠释初等数学的核心知识及重要的数学思想方法内容来审视和理解初等数学的问题。下面结合具体的实例来谈谈高等数学知识在中学数学中的应用。

一、拉格朗日中值定理为背景的初等数学问题：以拉格朗日中值定理为背景的问题在近几年高考中频频出现

解：（1）略。

总结：拉格朗日中值定理是高等数学中的一个重要定理，是解决函数在某一点的导数的重要工具，不少高考压轴题以导数命题，往往可以用拉格朗日中值定理求解，这些题目如果用初等数学知识求解，则需要构造新函数，且往往计算量较大，但用拉格朗日中值定理，则可较快地解决问题，体现高等数学的优越性，同时开拓学生的解题思路，激发学生的学习兴趣。

二、凹凸曲线问题在初等数学中的运用

直观形式：

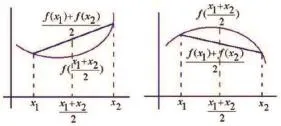
注：本题如果利用初等数学知识去解决，将会十分复杂，若利用对数函数的凹凸性则十分便捷，同时可开拓学生视野。

高等数学在初等数学中的应用远不只这些，但是通过上述问题我们不难发现，运用高等数学的知识可以大大简化问题的解决过程，开阔学生的视野，站在更高的维度去认识问题的本质与核心，提高学生对数学问题认知的深度，进而激发学生学习数学的积极性与主动性。

[1]吴冬梅.苏教版高中数学解题数学的有效性研究[J].数理化解题研究，2017（09）.

[2]黄春华.技巧 策略 思维——高中数学解题的三重境界[J].数理化解题研究，2015（09）.

[3]周瑞明.挖掘题目隐含条件,寻找解题突破口——谈一道高考试题的探究历程对解题教学的启示[J].数学教学通讯，2014（33）.

book=4,ebook=6