高校课堂质量的AHP—熵权模糊综合评价法

赵海青

摘 要：文章建立了课堂质量的综合评价体系，运用层次分析（AHP）法和熵权法分别赋予评价指标的主观和客观权重，并复合成综合权重，再对课堂质量进行模糊综合评价，由此提出了一种较科学的主客观相结合的AHP-熵权模糊综合评价法，并结合实例作了说明。

关键词：课堂质量；层次分析法；熵权法；模糊评价；评价指标

中图分类号：O221 文献标志码：A 文章编号：2096-000X（2017）14-0194-03

Abstract： This paper established a comprehensive evaluation of the quality of the classroom system. Using analytical hierarchy process （AHP） to provide the evaluation method and entropy method of subjective and objective weights， combine them into a comprehensive weight， and conduct a fuzzy comprehensive evaluation of the teaching quality， this paper proposes a more scientific combination of subjective and objective AHP entropy fuzzy comprehensive evaluation method， and illustrates it with some examples.

Keywords： classroom quality； AHP； entropy method； fuzzy evaluation； evaluation index

随着高校教学评价活动的深入开展，以专家教学督导组和学生共同的课堂质量评教活动方兴未艾，这是了解教师教学活动的有效途径。课堂质量评价主要是为了了解学生对任课教师在各教学环节的综合反馈，研究提高课堂质量的措施，为高校教学改革和教学管理提供有价值的依据，逐步建立和完善一套评价课堂质量的制度体系。及时发现并改进存在的不足，提高教师的课堂教学水平，有利于优化师资队伍，获取最佳的教学效果。由于某些定性评价指标的存在，增加了评价工作的难度，本文基于多准则决策的主客观相结合的评价方法，提出了AHP[1]-熵权模糊综合评价法[2]，对教师的课堂质量进行综合的考评。

一、建立评价体系模型

（一）层次分析法赋予主观权重

层次分析法（Analytical Hierarchy Process 简称AHP）是多准则决策领域常用的一种方法，是思维数学化的过程，它将复杂问题分解为不同的组成因素，按各因素之间的相互关联度和隶属支配关系，形成递阶层次结构。通过两两比较的方式，就每一层次诸多因素的相对重要性给以定量表示，并利用数学方法确定出每一层次各因素的权值。方法如下：

1. 建立递阶层次结构

把研究问题中的各因素按不同层次聚集组合，使之条理化、层次化，建立一个多层次分析的结构模型。

2. 构造判断矩阵

进行指标间的两两比较，得出成对因素的相对重要性，为了使判断决策量化，建立判断矩阵A，一般采用1～9级标度法。

3. 层次排序权重及一致性检验

对于判断矩阵A，计算满足AW=？姿maxW的特征值？姿max和特征向量W。W为？姿max的归一化特征向量，表示同一层次中各因素对于上一层某个目标相对重要性排序权值。

在解决实际问题时，由于客观事物的复杂性、决策者识水平和偏好的影响，对事物的认知往往会带有一定的主观片面性及模糊性。为确保AHP法结论的可信度和合理性，须把判断矩阵的偏差限制在合理范围内，可根据公式 CI=（？姿max-n）/（n-1）计算一致性指标CI；根据公式CR=CI/RI计算随机一致性指标CR（平均随机一致性指标RI可查表），当CR<0.1时，可认为判断矩阵满足一致性的要求。

（二）熵权法赋予各指标客观权重

1. 依各指标的实际得分情况，构造决策矩阵P（标准化， 归一化）；

2. 计算第j个指标的熵值：

3. 计算第j个指标的变异程度系数Dj：

4. 计算第j个指标的熵权值lj（客观权重）：

（三）确定综合权重

利用各指标的熵权值对AHP法主观权重进行复合修正，得出B-C层次的复合权重WB-C，再依WC=WB-CWB得出指标的综合权重。

（四）模糊综合评价

确定各指标的综合权重后，就需对参评课堂进行模糊评价。可设定评语集E=（优，良，中，较差，差），确定评语集的标准隶属度U=（0.9，0.7，0.5，0.3，0.1），以便得到直观的结果。根据学生对课堂教学的评价情况，建立模糊评价矩阵R，计算模糊隶属度Ti=Ri×UT，得出最终隶属度的分值Q=■WCTi，Q？缀[0，1]。

二、应用实例

华北电力大学为了进一步优化师资队伍，提高课堂质量，积极开展教学督导组和学生共同的优秀课堂评教活动。为了能清晰、准确地掌握评价体系的相关情况，对课堂质量做出客观公正的综合评价，构建了二级递阶结构评价模型。

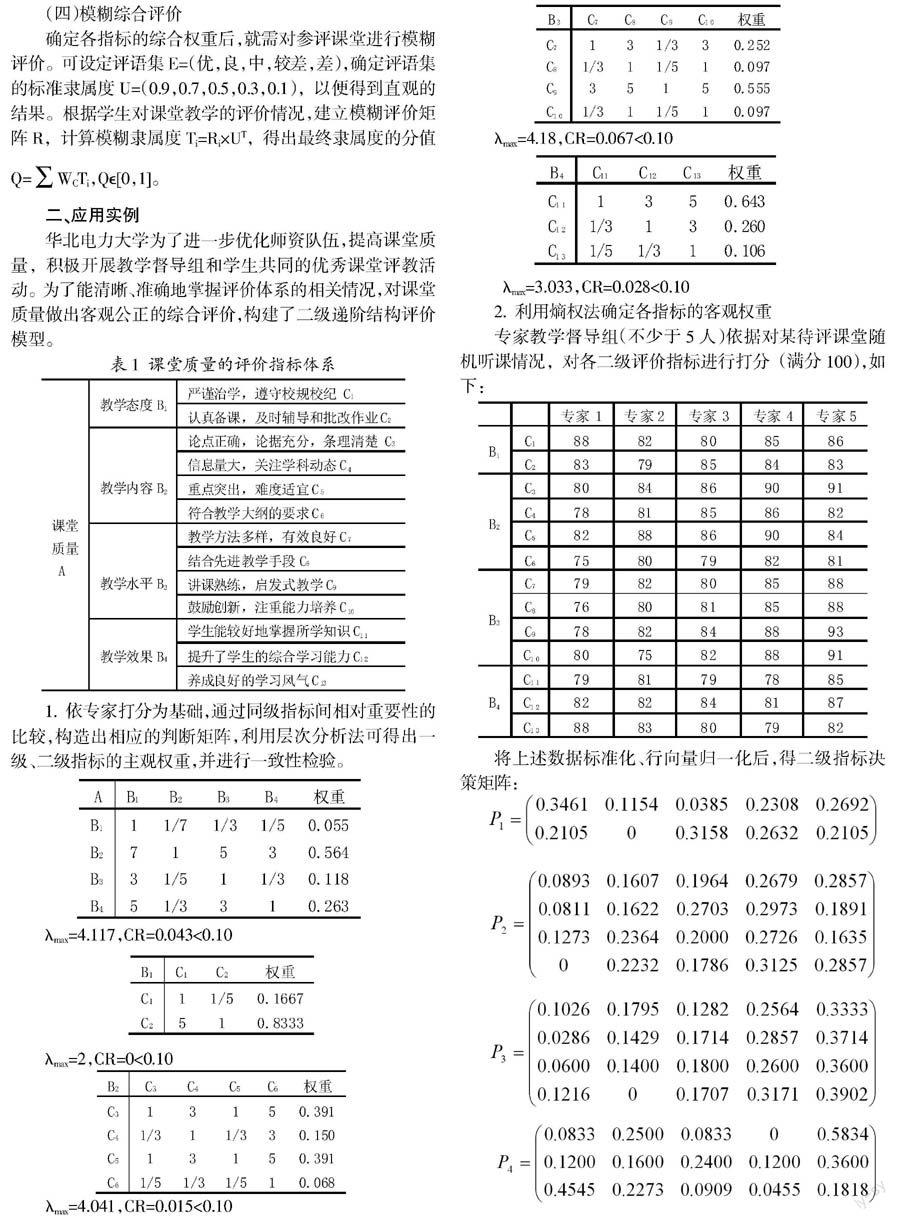
表1 课堂质量的评价指标体系

1. 依专家打分为基础，通过同级指标间相对重要性的比较，构造出相应的判断矩阵，利用层次分析法可得出一级、二级指标的主观权重，并进行一致性检验。

？姿max=4.117，CR=0.043<0.10

？姿max=2，CR=0<0.10

？姿max=4.18，CR=0.067<0.10

？姿max=3.033，CR=0.028<0.10

2. 利用熵权法确定各指标的客观权重

专家教学督导组（不少于5人）依据对某待评课堂随机听课情况，对各二级评价指标进行打分（满分100），如下：

将上述数据标准化、行向量归一化后，得二级指标决

策矩阵：

依公式（1）（2）（3），可计算出各指标的熵权值为：

3. 根据熵权值对AHP法的主观权重进行修正

4. 计算出各指标的综合权重为：

5. 计算最终隶屬度

依公式可得模糊隸属度：

Ti=（0.76 0.80 0.82 0.80 0.78 0.76 0.70 0.78 0.80 0.80 0.76 0.84 0.86） 最终隶属度为Q=0.78，属良好水平。

三、结束语

本文运用AHP法与熵权法所确定的指标主客观权重，复合得出综合权重，再依模糊评价法计算出综合隶属度。这样可充分利用被评价课堂指标的信息量，使评价结果更加接近实际。由于综合隶属度真实地反映了任课教师的课堂教学质量，教务处可对综合评价得分较低的教师进行针对性的培训和指导（如开展优质课堂观摩等活动），提高他们的教学水平，以便促进教师队伍的整体优化。

参考文献：

[1]刘新宪.选择与判断-AHP决策[M].上海：上海科学普及出版社，1988.

[2]张宗元.模糊数学入门和在建筑管理中的应用[M].中国建筑工业出版社，1991.