VMD与MCKD在轴承故障诊断中的应用与研究*

王建国，陈 帅，张 超

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

VMD与MCKD在轴承故障诊断中的应用与研究*

王建国，陈 帅，张 超

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

针对传统解调分析难以提取轴承故障信息的这一特征，提出了一种变分模态分解(variational mode decomposition，VMD)与最大相关峭度解卷积(maximum correlated kurtosis deconvolution，MCKD)相结合的滚动轴承故障诊断方法。首先对轴承故障信号进行进行VMD分解并得到一系列窄带本征模态函数(intrinsic mode functions，IMFs)；然后对各个IMF分量进行MCKD降噪，突出故障冲击成分；最后对降噪后的信号进行包络解调分析完成轴承的故障诊断。仿真信号和轴承故障振动信号的分析结果表明，基于VMD和MCKD的轴承故障诊断方法能够准确地获取轴承故障特征频率。

变分模态分解；最大相关峭度解卷积；本征模态函数；故障诊断

0 引言

滚动轴承是机械系统中非常重要的零部件之一，起到支撑转轴运转，维系机械系统正常运行的作用。因此，采用一定的技术手段对滚动轴承故障进行诊断从而确定故障类别、部位以及损伤程度意义重大。由于振动传输路径极其复杂，且通过传感器提取出来的振动信号具有非平稳特征，反映状态信息的能量也很微弱，给故障诊断带来了困难。如何从非平稳的振动信号中提取出故障特征信息是轴承故障诊断的关键[1-2]。

为了提取轴承故障特征，小波变换(wavelet transform，WT)[3]、经验模态分解(empirical mode decomposition, EMD)[4]、局部均值分解(local mean decomposition ,LMD)[5]等方法被引入故障诊断领域并取得了一定的成果，但是小波变换一旦选择了小波基及分解尺度，所得到的结果是某一固定频带的信号，从这一点上来讲，小波分析不具有自适应性；EMD和LMD方法虽然可以自适应的将复杂的多分量分解为一系列的分量，但是存在严重的模态混叠以及端点效应。

变分模态分解(variational mode decomposition, VMD)是一种非递归的分解方法[6]，在求解变分模型中通过不断对本征模态函数(intrinsic mode functions，IMFs)的中心频率和带宽进行更新，达到自适应的分解。相比于EMD和LMD，VMD其本质是一组自适应的维纳滤波器，因此不存在由于包络问题和递归运算产生的模态混叠和端点效应。

当轴承发生故障时，由于微弱的故障特征信号往往被强噪声所淹没，VMD分解后的各个IMF分量中依然残留一定量的噪声，因此有必要对各个IMF分量进行消噪处理。而最大相关峭度解卷积(maximum correlated kurtosis deconvolution，MCKD)[7]作为一种性能良好的降噪方法已经引起了科研工作者的广泛关注。唐贵基和王晓龙[8-9]将MCKD用于齿轮和轴承故障信号的降噪，并针对MCKD中滤波器的长度以及周期参数难以确定的问题提出了自适应MCKD方法。

基于此，本文提出一种基于VMD和MCKD的轴承故障诊断方法，并通过仿真信号和实测轴承故障信号验证所提方法的有效性。

1 变分模态分解

VMD是2014年新提出的信号分解方法，通过求解约束变分问题将任意复杂多分量信号自适应的分解为一系列基于中心频率与有限带宽的IMF分量。在求解过程中各IMF分量的中心频率和带宽随着迭代过程不断更新[10]。假定对于任意轴承振动信号y(t),则可以构造以下约束变分问题：

(1)

其中，{yk}={y1，y2，y3，…，yk}和{wk}={w1,w2,w3,…,wk}分别为IMF分量和中心频率的集合。

使用朗格朗日因子λ(t)和二次惩罚因子α将以上约束优化问题转化为无约束优化问题，其增广的拉格朗日形式可表示如下：

(2)

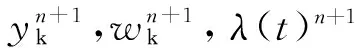
(3)

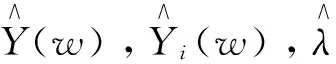
更新后各IMF分量的中心频率可以通过下式求得：

(4)

2 最大相关峭度解卷积

轴承故障信号中存在的噪声会降低信号的可读性。而MCKD是以相关峭度作为评价指标，可以一定程度上降低信号中的噪声成分，提升原始信号的峭度[11]，从而充分突出轴承故障信号中被噪声淹没的周期冲击成分。

当轴承发生故障时，由于出现局部碰撞，会产生周期性冲击信号x，该冲击信号x传递到传感器上时，由于传输路径的影响会被衰减，并且会掺杂大量的噪声成分e，假设路径传输衰减响应为h，则由传感器拾取到的实测信号y可表示为：

y=h·x+e

(5)

而MCKD算法的本质是寻找一个滤波器，通过实测信号y恢复冲击信号x，从而达到抑制噪声和突出故障冲击成分的目的，即:

(6)

式中:f=[f1,f2,…fL]T为滤波器的系数组合,L为滤波器的长度。

在MCKD中是以相关峭度作为评定恢复信号x性能的指标。当相关峭度达到最大时，则认为是MCKD处理的最终结果。对于任一信号yn，相关峭度定义为：

(7)

其中：T为冲击信号的周期；M为位移数。

MCKD算法的目标函数为：

(8)

即求解方程:

(9)

求解方程后得到的滤波器系数组合用矩阵形式表示如下:

(10)

其中：

式中：r=0,T,2T,…,mT

将得到的滤波器系数组合f带入公式(6)，即可得到周期性冲击信号x。

3 VMD和MCKD的轴承故障诊断方法

将加速度传感器采集到的轴承振动信号进行VMD分解，得到若干个基于中心频率和有限带宽的IMF分量。然后对各个IMF分量进行MCKD降噪。最后求取各个IMF分量的包络谱，在包络谱中找寻该型号轴承对应的故障特征频率，即可确定轴承的故障类型。实现流程如图1所示。

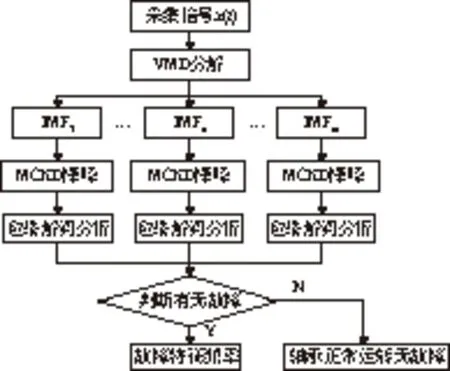
图1 轴承故障诊断流程

4 仿真分析

为了验证本文提出方法的有效性，根据轴承故障的冲击特征构造如下仿真信号：

x(t)=x1(t)+x2(t)+x3(t)

(9)式中，x1(t)为周期信号，每周期内冲击成分为2e-800tsin(10000πt)，冲击周期为1/160s，即周期性冲击振动频率f0=160Hz;x2(t)=0.8×sin(150πt)×sin(2000×πt)为低频信号；x3(t)为幅值标准差为1的噪声信号；t=0:1/40000:0.05s。仿真信号及其各成分如图2所示，图3是仿真信号的包络谱，由于受到强背景噪声干扰，从包络谱中难以找到故障特征频率。

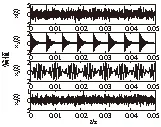
图2 仿真信号x(t)及其各成分的时域波形

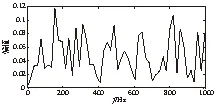
图3 仿真信号的包络谱

对仿真信号进行VMD分解，得到6个IMF分量如图4所示。图5是IMF5分量的包络谱，从包络谱中可以看到故障特征频率f0及其二倍频2f0，但是其他的倍频成分不清晰。

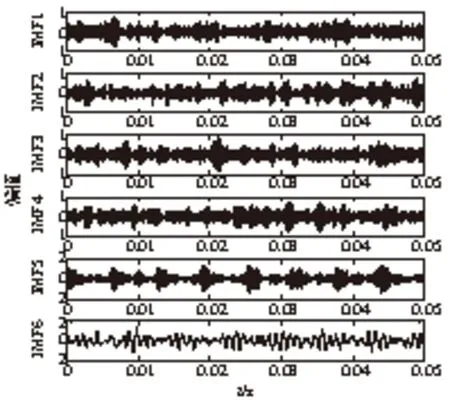
图4 仿真信号的VMD分解结果

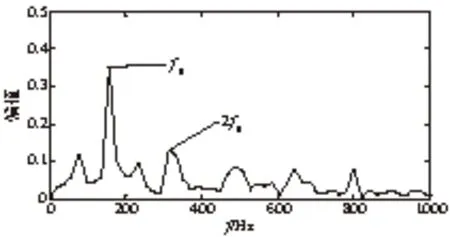
图5 IMF5分量的包络谱

对IMF5分量进行MCKD降噪处理，得到的时域波形如图6所示，从时域波形中能看到较为明显的周期故障冲击成分，图7是MCKD降噪后信号的包络谱，包络谱中呈现的故障特征频率及其1至5倍频非常清晰。故本文提出的基于VMD与MCKD轴承故障诊断方法比单纯地使用VMD分解效果好。

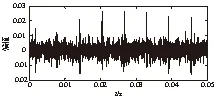
图6 MCKD降噪后信号

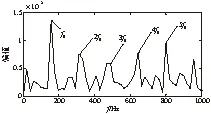
图7 MCKD降噪后信号的包络谱

5 应用实例与分析

实验所用的故障轴承振动数据来自美国凯斯西储大学，测试轴承为支承电机驱动端的6205-2RS深沟球轴承。选用采样频率为12kHz下的轴承内圈故障信号的4000个数据点进行分析，滚动体节径为7.94mm，轴承节径为39.04mm，滚动体个数为9，接触角为0°，轴承转速为1750rpm。通过计算得轴承的转频fr为29.17Hz。内圈故障频率fi为157.94Hz。

内圈故障轴承信号的时域波形如图8所示。由于噪声的干扰，从时域波形图中难以辨别轴承故障信息。图9是故障信号的频谱图，信号的能量主要集中在高频段，但也未找到故障对应的特征频率。

图8 内圈故障轴承信号时域波形图

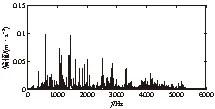
图9 内圈故障信号频谱图

对原始信号进行VMD分解，分解结果如图10所示。得到了6个分量IMF1-IMF6。

图10 VMD分解结果

图11是IMF5分量对应的包络谱，图中出现了三条清晰的谱线，58.59Hz对应着轴承的二倍转频；158.2Hz、313.5Hz分别对应着轴承内圈故障特征频率及其二倍频。由于实际中来自于轴承振动信号通常是复杂的，由多个振源共同激发，因此得到的各频率和理论频率存在微小的偏差。但是图中的内圈故障特征频率不是处于最高峰，而且故障特征频率的各阶倍频峰值较低。

图11 内圈故障信号包络谱

对IMF5分量进行MCKD降噪处理，图12是降噪后的时域波形图，图13是降噪后信号的包络谱。包络谱中的故障特征频率158.2Hz峰值处于最高的位置，与图11相比，图13中的轴承二倍转频成分有所降低，轴承故障特征频率158.2Hz、及其二倍频313.5Hz非常清晰，而且还出现了故障特征频率的三倍频471.7Hz的成分。

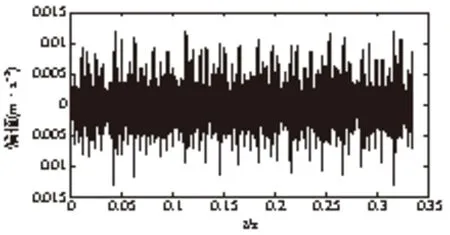
图12 MCKD降噪后信号

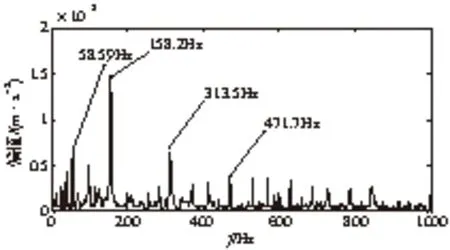
图13 MCKD降噪后信号包络谱

由此再一次说明本文提出的基于VMD和MCKD的轴承故障诊断方法比单纯地使用VMD分解效果好。

6 结论

本文利用VMD方法对实测复杂多分量轴承故障信号进行VMD分解，将故障信号按照频域进行自适应划分；然后，采用MCKD方法对各IMF分量进行降噪处理突出故障周期成分；最终利用共振解调技术找到轴承故障特征频率，从而完成轴承的故障诊断。通过对仿真和实验结果的分析，可得如下结论：

(1) VMD方法可以较好将复杂的多分量信号分离开。

(2) MCKD方法能够较好地抑制背景噪声，突出轴承故障信号中的周期冲击成分。

(3) 基于VMD与MCKD相结合的滚动轴承故障方法比仅使用VMD方法进行故障诊断效果好，进而为工程实际应用打下坚实的基础。

[1] 何正嘉，袁静，訾艳阳.机械故障诊断的内积变换原理与应用[M]. 北京：科学出版社，2012.

[2] 任学平，王朝阁，张玉皓，等. 基于DT-CWT和MCKD的滚动轴承早期故障诊断方法[J]. 仪表技术与传感器，2016(5)：106-110.

[3] MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Trans PAMI, 1989,11 (7) :674-693.

[4] 徐康，黄民. 基于EMD 和DHMM 的刀具故障诊断[J].组合机床与自动化加工技术，2016(7)：89-91.

[5] 丁瑞成，黄友锐，陈珍萍，等. LMD和SVM相结合的电机轴承故障诊断研究[J]. 组合机床与自动化加工技术，2016(8)：81-84.

[6] Dragomiretskiy K, Zosso D. Variational mode decomposition[J].IEEE Tran on Signal Processing. 2014,62(3): 531-544.

[7] MCDONALD G L,ZHAO QING, ZUO M J. Maximum correlatted kurtosis deconvolution on geartooth chip fault detection[J]. Mechanical Systems and Signal Processing, 2012, 33: 237-255.

[8] 唐贵基，王晓龙.自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报，2015，35(6)：1436-1444.

[9] 唐贵基，王晓龙. 最大相关峭度解卷积结合稀疏编码收缩的齿轮微弱故障特征提取[J]. 振动工程学报,2015,28(3):478-486.

[10] 刘长良，武英杰，甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报，2015，35(13):3358-3365.

[11] 武兵，贾峰，熊晓燕. 基于最大相关峭度反褶积的轴承故障诊断方法[J]. 振动、测试与诊断，2014，34(3)：570-575.

(编辑 李秀敏)

Application and Research of VMD and MCKD in Bearing Fault Diagnosis

WANG Jian-guo, CHEN Shuai, ZHANG Chao

(School of Mechanical Engineering, Inner Mongolia University of Science and Technology, Baotou Inner Mongolia 014010, China)

Aiming at the feature that it was difficult for the traditional envelope demodulation analysis to extract the bearing fault information, a method of rolling bearing fault diagnosis,which is based on variational mode decomposition(VMD) and maximum correlated kurtosis deconvolution(MCKD) was proposed. First of all, bearing fault signal was decomposed into a series of narrow band intrinsic mode functions(IMFs) using VMD method. Then, the noise of IMFs was eliminated and the fault information was enhanced by using MCKD method. Finally, the denoised signal was done through envelope demodulation analysis to complete the bearing fault diagnosis. According to the vibration signal of fault bearing and simulation results, the bearing fault diagnosis method based on VMD and MCKD can extract the characteristic frequency of bearing faults more effectively.

variational mode decomposition; maximum correlated kurtosis deconvolution; intrinsic mode function; fault diagnosis

1001-2265(2017)05-0069-04

10.13462/j.cnki.mmtamt.2017.05.018

2016-08-22；

2016-09-02

国家自然科学基金资助项目(51565046)；内蒙古自然科学基金资助项目(2015MS0512)；内蒙古高等学校科学研究资助项目(NJZY146)

王建国(1958—)，男，呼和浩特人，内蒙古科技大学硕士生导师，博士，研究方向为机电系统智能诊断与复杂工业过程建模；通讯作者：陈帅(1990—)，男，安徽安庆人，内蒙古科技大学硕士研究生，研究方向旋转机械故障诊断，(E-mail) 1054543069@qq.com。

TH162；TG506

A