数学史与小学数学教师专业发展
汪晓勤
一、引言
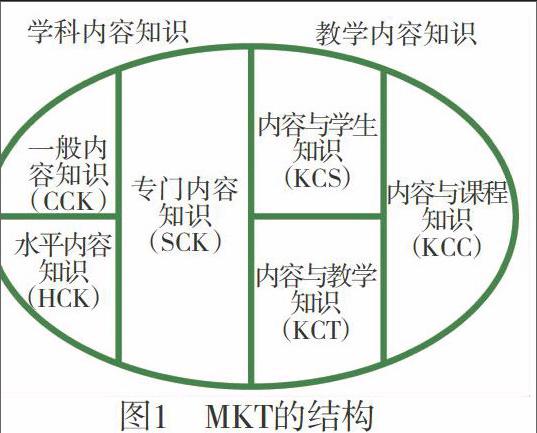
小学数学教师专业发展的目标包括知识、信念、能力等方面,其中,教师的知识可以用美国数学教育家鲍尔提出的MKT理论来刻画。所谓MKT,是Mathematical Knowl-edge for Teaching的简称,指的是“完成数学教学工作所需要的数学知识”,其组成成分如图1所示。
“一般内容知识”是指除教学外,在其他背景下也使用的数学知识和技能;“专门内容知识”是指教学所特有的数学知识和技能;“水平内容知识”是关于整个数学课程中数学主题之间联系的知识;“内容与学生知识”是指对学生的了解和对数学的了解相结合的知识;“内容与教授知识”(对应于范良火的“教学的内容知识”和“教学的方法知识”)是指对如何教授的了解和对数学的了解相结合的知识;“内容与课程知识”(对应于范良火的“教学的课程知识”)是指关于课程大纲、课程标准、教科书、教学材料以及其他教学资源的知识。
近年来,数学史在小学数学教学中的意义日益受到人们的关注,数学史融入小学数学教学的实践探索也日益增加。我们在开发HPM教学案例(即“融入数学史的教学案例”)的过程中,确立了“大学研究人员和小学教师密切合作”的模式,使得小学数学教师在没有受过数学史教育或缺乏数学史材料的情况下,也能走进HPM的世界。本文拟回答以下问题:数学史与小学数学教师的MKT之间有何关系?
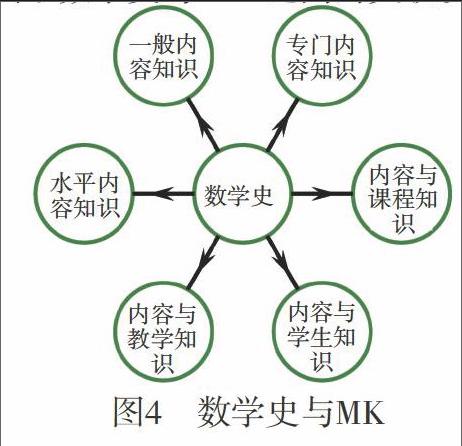
二、数学史与MKT
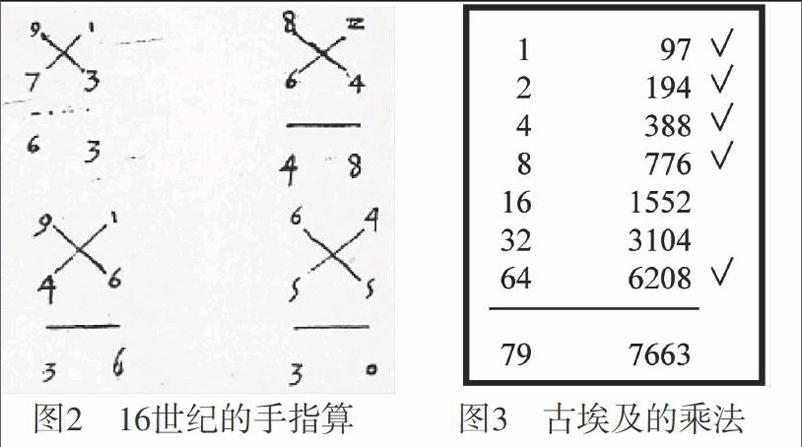
虽然许多一般内容知识是教师在学生时代习得的,但在数学教学中,教师不断会遇到新的一般内容知识,而数学史往往提供了这样的知识,如计算两个正整数乘积的不同方法。图2所示是16世纪盛行于欧洲的“手指算”,而图3则给出了古埃及人计算97~79的方法。
为了解决教学中所遇到的各类“为什么”问题,教师需要拥有丰富的专门内容知识。三角形面积公式和三角形内角和定理属于一般内容知识,但它们的推导或证明方法则属于专门内容知识。这类知识往往源于数学史。如,中国古代数学家用“出入相补”法证明三角形、梯形面积公式,古希腊哲学家泰勒斯通过拼图发现三角形内角和定理。圆周率的近似值为3.14,这属于一般内容知识,但得到该近似值的具体方法则属于专门内容知识,刘徽的割圆术就是其中之一。至于对诸如“为什么未知数用字母x来表示”“小数是很小的数吗”之类的问题,教师只能从数学史中寻找答案。
数学的历史是一面镜子,前人在数学概念理解过程中所遇到的困难和障碍,往往也是今天数学课堂上学生会遇到的困难和障碍。从数学理解的意义上说,了解历史,也就了解了学生。尽管在古代中国,数学家出于解方程组的需要而引入了负数,但在西方,18世纪还有人问:“世界上还有什么小于一无所有?”直到19世纪,还有数学家认为负数是“荒谬的”。负数大小比较问题也完全没有我们想象的那样简单。历史上,笛卡儿、牛顿、欧拉、波尔查诺、阿贝尔等数学家都有不同于今天的理解,他们的观点都可以归结为“数轴上离原点越远的数越大”或“绝对值越大,数越大”。据此有-4>-1。关于负数及其序关系的认识论障碍提示我们:学生在学习负数概念时必会遭遇困惑或出现错误。数学史丰富、深化了内容与学生知识。
历史上,一个概念、公式、定理、法则甚至一个数学分支学科的产生都有其内在或外在的动因,也都有演进的过程。这种动因和过程为教师“怎么教”有关知识点提供了参照。例如,分数有分割分数和度量分数两类。究竟如何引入分数概念?分数的历史告诉我们,人类首先是在物品分割的情境中认识和运用分数的,因此,分割分数是理所当然的教学选择。
数学史是一座宝藏,其中含有取之不尽、用之不竭的教学素材和思想养料,因而是数学教师的重要教学资源。针对某一个特定的知识点,教师关于相关数学史素材的知识是内容与课程知识不可或缺的一部分。另一方面,数学史知识也有助于教师对小学数学知识体系的理解。例如,关于教科书中“小数和分数孰先孰后”的争论,需要参照数学史加以研究。
三、HPM教学案例分析
1.角的初步认识。在数学史上,“角”是一个具有多重属性、争议很多、很难刻画清楚的几何概念。古希腊哲学家泰勒斯曾将“相等的角”称为“相似的角”。后来,亚里士多德将“角”视为“弯曲的线构成的图形”,并且也将两个相等的角称为“相似的角”。可见,早期哲学家是从“形”的角度去看待“角”的,即赋予“角”以“质”的属性。
在《几何原本》中,欧几里得从两线之间位置关系的角度去刻画“角”:“角是平面上相遇且不在同一直线上的两条线彼此之间的倾斜度”。另一方面,欧几里得分别将“直角”“锐角”“钝角”定义为:
若一直线与另一直线构成的两个相邻的角相等,则称这两个角为直角;
钝角是大于直角的角;
锐角是小于直角的角。
用“等于”“大于”和“小于”来比较两个角,欧几里得又赋予“角”以“量”的属性。而徐光启在翻译《几何原本》时创用“直角”“钝角”“锐角”三个名称,又赋予角以“質”的属性。普罗克拉斯认为,必须同时从质、量和关系三个方面来定义角,因为单独采用某一个方面,都未能完善地刻画该概念。
在二年级教学案例“角的初步认识”中,教师借鉴角概念的发展历史,按照从“质”到“量”再到“关系”的顺序展开教学(如图5)。首先,让学生列举生活中的角的实例,并描述什么是角。学生提到“尖尖的”“像屋顶一样”“像L一样”,等等,他们显然都是从“质”的角度来认识“角”。接下来引入情境:“鸟妈妈对鸟宝宝们说,谁的嘴巴张得大,就把小虫喂给谁吃。”让学生判断,图中哪一只鸟宝宝能吃到小虫。在学生说出鸟宝宝嘴巴大小顺序之后,教师让他们说出角的大小比较方法,从而引导学生从“量”的角度来认识角。接着,让学生对不同大小的角进行分类,并探讨:为什么小于直角的角称为“锐角”,大于直角的角称为“钝角”?学生从“质”的角度,用“锐利”“迟钝”“扎人疼”“扎人不疼”等来解释。在练习之后,教师通过将不同的角的顶点和一边重合,引导学生发现,角可以通过将一边旋转得到,从而让学生从“关系”(即两条边之间的位置关系)的角度来认识角。
HPM视角下的“角的认识”的教学,让学生经历了角概念的产生和发展过程,在课堂上获得探究机会,感受成功的喜悦;当教师总结,学生比较角的大小的方法、关于锐角和钝角的解释,都与历史上数学家的想法相似,这大大增强了学生的自信心,让他们感受到自己也是小数学家。
本案例中,角概念的历史为教学设计提供了参照,是教师在HPM教学设计与实施过程中所学到的内容与教学知识;同时,对于角的三重属性(质、量、关系)的认识,使教师关于角的一般内容知识得到了扩充与完善。数学教育研究表明,学生对于角的认识具有一定的历史相似性,古人在对角的认识方式以及认识过程中所遭遇的困难(角的多重属性、特殊角(零角和平角))会再现于今日的数学课堂中,因而角的历史对教师而言是一种内容与学生知识。在教师接触HPM之前,并未思考过“锐角”“钝角”的辞源问题,角概念的历史为教师弥补了专门内容知识。此外,以角的历史为参照,教师开始审视课本上的内容,拓展了自己的内容与课程知识。
2.一位数与二位数的乘法。历史上,求两个正整数乘积的算法很多。1430年左右,在意;kN的一份数学手稿中,出现了一种名为“格子算”的乘法。图6是世界上第一部印刷出版的算术教科书《特雷维索算术》(1478年)中的格子算。
在三年级教学案例“一位数乘二位数”中,教师通过实际情境,引入32×5,让学生独立给出自己的算法;在学生给出各种各样的算法之后,教师引入图7所示的格子算,让学生加以解释,并与竖式算法进行比较。在课堂小结部分,教师让学生思考:为什么格子算现在不用了?
格子算的引入促进了学生对乘法算理的理解,也开阔了他们的视野,感悟到自己的解法只是很多解法中的一种。在古今方法的对比中,学生体会到现代竖式算法的优点,但也有许多学生更喜欢格子算。对于“为什么现在不用格子算”这一问题,有学生给出的解释是:“格子算传着传着就失传了”,不知不觉中,学生对于数学知识已经有了历史感,这种历史感让他们更加亲近数学。
在本案例中,格子算拓宽了教师关于乘法的一般内容知识。对于格子算背后的算理、格子算与竖式算法之间联系的认识,丰富了教師关于乘法的专门内容知识。在教学设计过程中,教师在大学合作者的指导下,查阅有关乘法的历史文献,丰富了自己的内容与课程知识。
3.圆的面积。历史上,古希腊数学家阿基米得(Archimedes,公元前287-前212)最早给出圆面积的准确公式:圆面积等于一条直角边长为圆半径、另一条直角边长为圆周长的直角三角形面积。这里,阿基米得将圆“转化”为更简单的三角形,从而得出了圆面积公式。
虽然阿基米得最终借助穷竭法来证明关于圆面积的命题,但他一开始是如何将圆和三角形建立联系的呢?从微积分的角度看,圆面积的不同解决方法取决于“微元”的不同选择,如图8所示。
阿基米得可能使用了第一种方案。如图9,想象圆由一些长短不同的细绳围成,将圆“剪开”,并将各绳“拉直”,一端对齐,得到一个直角三角形,其长直角边等于圆的周长,短直角边等于圆的半径。
17世纪德国数学家开普勒(J.Kepler,1571-1630)则选择第二种方案建立起圆与三角形之间的联系:将圆分割成无数个顶点在圆心、高为半径的小“三角形”(实为小扇形,但将圆分得越细,小扇形越接近三角形)。将这些小“三角形”都转变成等底等高的三角形,最后,它们构成了一个直角三角形,如图10所示。
在六年级教学案例“圆的面积”中,教师讲述开普勒求圆面积和酒桶体积的故事,并采用开普勒的方法来推导圆面积公式:先让学生回顾“等底等高的三角形面积相等”的事实;再作圆内接正十二边形,利用几何画板(PPT展示),依次对其中的12个小三角形进行等积变换,从而将其变成等积的直角三角形;然后作正二十四边形、四十八边形、九十六边形,相应得到等积的直角三角形,让学生直观感受并猜想这些直角三角形与圆面积之间的关系。
开普勒求圆面积的方法引起学生浓厚的兴趣,而开普勒的故事则让学生感受到数学背后的人文精神。
在本案例中,开普勒的方法拓展了教师的专门内容知识和内容与教学知识;同时,该方法建立了圆面积公式和三角形面积公式之间的联系,丰富了教师的水平内容知识。
以上我们看到,数学史不仅有助于发展和完善教师的MKT,而且在很多情况下就是教师MKT的不可或缺的一部分;数学史融入数学教学的实践对于小学数学教师的专业发展有着巨大的促进作用。
我们期待,“数学史与数学教育”能够成为小学数学教师在职培训的重要课程,我们也期待,有更多的小学数学教师走进HPM、实践HPM,让他们的数学课堂洋溢数学文化的芬芳。