太阳帆板联动机构同步机理分析与动力优化

杨文淼，时军委

(上海宇航系统工程研究所，上海201108)

太阳帆板联动机构同步机理分析与动力优化

杨文淼，时军委

(上海宇航系统工程研究所，上海201108)

通过对绳索联动机构(CCL)进行等效简化，分析CCL同步展开机理，并建立数学模型。详细推导了含CCL联动系统的动力学方程，以某型太阳帆板展开同步性为例，仿真分析展开动力学过程以及大幅不同步产生的原因。以整个展开过程中最大不同步量最小为优化目标，建立联动系统优化模型，并采用序列二次规划算法(SQP)对驱动力矩参数进行了优化设计。相对驱动力矩为正值的传统设计方法,根部驱动力矩为负值的优化结果有效降低联动绳索负载，改善了太阳帆板展开同步性。

太阳帆板；展开动力学；优化设计；序列二次规划

0 引 言

在航天器发射阶段，太阳帆板一般呈收拢状态，在航天器入轨以后，压紧释放机构解锁，太阳帆板在驱动卷簧的作用下实现展开。在太阳帆板展开过程中，为确保结构间不发生干涉，需要对太阳帆板展开过程的同步性进行控制。绳索联动机构(Closed cable loops, CCL)是目前最为常见的一种同步展开控制机构[1-8]，CCL由联动轮和联动装置绳索构成，为方便起见这里采用两段式展开结构进行说明，其构造如图1所示。在铰链O和铰链A处设置联动轮，并分别与卫星本体和太阳帆板固定，CCL利用链轮的传动原理，通过联动装置绳索在铰链间传递力矩，从而使太阳帆板的展开保持同步。显然CCL的性能直接影响太阳帆板展开的运动特性，对其同步作用机理进行深入研究具有重要的工程实际意义。联动装置绳索的刚度是影响CCL整体性能的重要设计参数，一般来讲提高其刚度有助于减小太阳帆板展开过程中的不同步性。但受到结构自身和材料性能等诸多限制，联动绳索的刚度不能无限提高。此外，增加绳索刚度的同时，也会引入更大的展开阻力作用，甚至影响太阳帆板的顺利展开。对于采用大质量惯量的太阳帆板系统来说，连接架与太阳帆板质量惯量差异巨大，仅靠调整钢丝绳的刚度来保证同步性得到的设计在工程中无法实施。

在CCL机理以及相关数学模型的建立方面，国内外学者均作了大量研究。文献[2-3]将CCL等效成被动控制系统，分析其参数对太阳帆板展开同步性的影响。文献[4]通过展开动力学仿真分析，设计了联动绳索的预置张力，并进行了合理性验证。文献[5]建立了联动展开机构参数化模型，对其进行了优化设计。文献[6-8]对采用绳索联动展开机构的卫星太阳翼进行了展开动力学分析。文献[9]将CCL联动装置产生的阻力矩等效成弹簧作用于铰链上，并对展开机构的力矩可靠性进行了分析。文献[10]建立了太阳翼板同步展开控制机构数学模型，对铰链展开式构型航天器进行了动力学仿真。此外,文献[11-13]均建立了CCL等效模型，并给出了具体的数学描述。现有研究集中在CCL的等效数学描述上，没有考虑惯量和驱动力矩等参数对含CCL展开系统同步性的影响。

本文综合考虑惯量和驱动力矩等影响因素，对某型太阳帆板展开过程进行动力学建模，仿真分析了大幅不同步产生的原因。以整个展开过程中最大不同步量最小为优化目标，建立联动系统优化模型。通过对力矩参数进行优化设计，有效降低联动绳索负载，改善了太阳帆板展开同步性。

1 CCL同步机理分析

1.1 CCL数学模型的建立

图2为CCL简化的等效模型。模型中R1=2R2，同步情况下，轴O的转角θ1与轴A的转角θ2应满足关系式：θ1=0.5θ2。在太阳帆板展开过程中，如果轴O和轴A处存在转角不同步现象，假设θ1>0.5θ2，联动装置绳索会出现受力不平衡现象，表现为一侧受到拉伸作用而加大绳索的张力，称之为紧边，而另一侧会因为绳索的相对松弛而减小绳索的张力，称为松边。绳索张力的不平衡会产生两个控制力矩作用T1和T2，T1在转动角度过快的轴O处表现为一阻力矩，T2在转动角度相对较慢的轴A处表现为一驱动力矩。

设联动绳索的线刚度为k，绳索的变形量为Δl，紧边和松边绳索张力表示为：

Ft=f0+kΔl

(1)

Fr=f0-kΔl

(2)

式中：Ft和Fr分别是紧边和松边的绳索张力，f0是绳索的预紧力，绳索变形量Δl=R1θ1-R2θ2。

系统不同步产生的控制力矩为：

T1=-(Ft-Fr)R1=-2kΔlR1

(4)

T2=(Ft-Fr)R2=2kΔlR2

(4)

考虑到绳索不能承受负张力，其最小张力为0。则当Ft=0时，控制力矩表达式为：

T1=-(Ft-Fr)R1=(f0-kΔl)R1

(5)

T2=(Ft-Fr)R2=-(f0-kΔl)R2

(6)

同理，当Fr=0时，控制力矩表达式为：

T1=-(Ft-Fr)R1=-(f0+kΔl)R1

(7)

T2=(Ft-Fr)R2=(f0+kΔl)R2

(8)

1.2 系统动力学方程

以两段式展开结构为例建立坐标系，如图3所示。

整个展开系统的动能可表示为：

(9)

其中：

m2L1L2cosθ2)

(10)

(11)

(12)

式中：θ1为连接架展开角度，θ2为帆板相对连接架展开角度，I1和I2分别为连接架和帆板绕O轴和绕帆板质心的转动惯量，L1和L2分别为连接架和帆板的长度，m2为帆板的质量。

系统的势能表示为：

V=k(Δl)2-M1θ1-M2θ2

(13)

式中：M1和M2分别为铰链O和铰链A处作用的驱动力矩。

系统的拉格朗日方程为：

(14)

对于保守力的广义力有：

(15)

由式(9)～(15)整理可得：

(16)

式中：2f1(θ2)为广义坐标上的广义惯量，2f2为广义坐标θ2上的广义惯量，f3(θ2)为耦合惯量。

在给定的初始条件下，解方程组(16)，可实现太阳帆板展开过程的仿真分析。

2 展开仿真分析与同步性动力优化

2.1 展开仿真分析

以某型太阳帆板展开过程为例进行了数值仿真。整个系统构型如图3所示，其中绳索联动机构中联动轮半径分别为R1=80mm和R2=40mm。连接架与帆板的长度分别为L1=2230mm、L2=7000mm。帆板各体的质量、惯量信息如表1所示。

表1 系统惯量参数Table 1 Inertia parameter of system

注：表中Ixx、Iyy、Izz、Ixy、Ixz、Iyz为惯量张量的分量，单位kg·m2。

取M1=6Nm，M2=9Nm，联动绳索刚度k=25N/mm，预紧力f0=60N对其进行展开动力学仿真分析。图4为展开角度时程曲线图，为方便比较，轴O处的角位移用2θ1表示。

从图4可以看出，两条曲线差异明显。进一步定量考察展开角度的差异，定义不同量为θ2-2θ1，不同步量随时间的变化曲线如图5所示。

从图5可以看出，最大不同步量为24°发生在展开到位时刻。进一步对广义坐标上的负载惯量进行分析，令作用于广义坐标θ1和θ2上的广义惯量分别为Iθ1和Iθ2，由式(12)可得：

(17)

Iθ2=I2+m2(L2/2)2

(18)

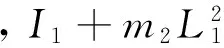
将太阳帆板相关参数代入式(17)～(18)得到广义惯量Iθ1和Iθ2随广义坐标θ2变化曲线(见图6)。

从图6可以看出，随着广义角θ2的增加，广义惯量Iθ1逐渐增大，而广义惯量Iθ2则保持不变。当驱动力矩确定后，两者的差异会造成展开过程中的不同步性，并且两者差异越大，不同步量越明显，进而对联动绳索的负载及刚度需求也越高。

图7给出了展开过程中绳索张力的时程曲线。对比图7和图5可以看出，联动绳索张力的变化随着不同步量的变化而变化。在整个展开过程中，联动绳索张力分布极不均衡，处于松边的绳索基本处于松弛状态，不提供张力；而处于紧边的绳索一直处于张紧状态，张力变化较大，当展开到位时达到最大值约为470N。

从图4～7可以看出，现有的联动绳索刚度值不能满足太阳帆板同步展开需要，且联动绳索负载较大。进一步对联动绳索刚度对展开不同步量的敏感性进行了分析，最大不同步量随联动绳索刚度k的变化曲线如图8所示。

从图8可以看出，随着联动绳索刚度k值的增大，最大不同步量逐渐减小，联动绳索刚度k越大，展开同步性越好。图中横虚线为10°线，该值是工程可接受的最大不同步量。由图8可知，当k≥170N/mm，才能满足工程需要。对于联动绳索直径有如下公式：

(19)

式中：Es是等效弹性模量，L为绳索长度，D是绳索直径。

绳索一般采用钢丝绳，其等效弹性模量为Es=57Gpa，本例中绳索长度L=4500mm，当k=170N/mm时，由式(19)可得绳索直径约为D=4mm。

显然该直径值在工程上是不能接受的。图8中竖点划线为工程可接受联动绳索刚度值k=32N/mm，此时绳索直径约为D=1.8mm。

2.2 展开同步性动力优化

由于绳索刚度的限制，依靠调整绳索刚度值不能满足帆板展开同步性要求。本文将驱动力矩M1和M2定为设计变量，研究驱动力矩的参数设计对含CCL展开系统同步性的影响。

首先需确定M1和M2的取值范围。由于CCL具有在各轴间传递力矩的作用，通过式(19)可知，作用在轴O和轴A处的全力矩MO和MA可表示为

MO=T1+M1

(20)

MA=T2+M2

(21)

为保证帆板展开过程中各铰链轴转角为正，即太阳帆板背离本体展开，需满足条件MO,MA>0。结合式(3)～(8)，考虑钢丝绳最大承载力fmax=1000N,可得：

(22)

(23)

由式(19)～(20)可以确定M1、M2的下限值分别为-80Nm和-40Nm。在此基础上考虑展开时间约束，确定M1、M2的合理取值范围为[-15Nm,15Nm]。

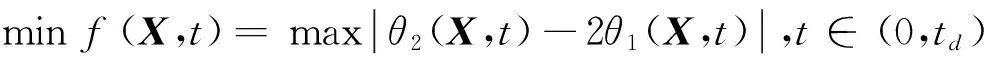
(24)

式中：X=[M1，M2] ,td=td(X)为帆板展开到位时间。

通过对设计变量进行迭代优化，最终得到帆板展开过程最大不同步量的最优结果为7.6°，此时M1和M2的优化结果分别为M1=-7094.9Nmm，M2=7803.6Nmm。

采用优化后的力矩参数，对太阳帆板展开过程进行动力学仿真分析，得到各典型时刻太阳帆板展开状态如图9所示。

图10为整个展开过程中轴O与轴A处展开角度时程曲线。从图10可以看出，优化后两条曲线基本吻合，同步效果明显。

图11为优化前后不同步量对比时程曲线。从图11可以看出，优化前最大不同步量约为24°，而优化后整个展开过程较为平稳，展开过程中的不同步量在3°以内。最大不同步量同样发生在展开到位时刻为7.6°，优化后的最大不同步量较优化前减小了67%。

图12为优化前后联动绳索张力的变化时程曲线。从图12可以看出，优化前联动绳索张力峰值约为480N。优化后展开过程中联动绳索的张力分布更为均衡，松边和紧边的张力变化均为50N左右，展开到位后联动绳索张力峰值约为220N，比优化前的张力峰值降低了54%。

对比优化前后的仿真结果可以看出，优化后CCL联动绳索张力分布发生了变化，在展开相当长的时间内，原来的紧边与松边发生了互换。产生这一现象的主要原因是，优化前后M1对轴O的作用由驱动力矩转化为阻力矩，这进而导致展开过程中值θ2<2θ1的符号发生了变化，从而使CCL产生的控制力矩由阻力矩转化为驱动力矩。

由图9～12可知，通过对M1和M2进行优化设计，有效降低了联动绳索的负载，使太阳帆板达到了良好的同步展开特性。此时，钢丝绳刚度为32N/mm，直径约为1.8mm为工程可接受设计。

3 结 论

本文基于CCL同步展开机理实现了对CCL联动系统的数学建模。详细推导了含CCL联动系统的动力学方程，仿真分析了某型号太阳帆板产生大幅不同步性的主要影响因素。采用序列二次规划算法对驱动力矩进行优化设计。相对传统设计方法，本文给出的根部驱动力矩为负值的优化结果使联动绳索负载降低54%，最大不同步量减小67%，优化效果明显。本文的结论可以为大惯量太阳帆板展开机构的设计优化提供理论依据。

[1] 谢宗武,宫钇成,史士财,等.空间太阳能电池阵列技术综述[J].宇航学报,2014,35(5):491-498.[XieZong-wu,GongYi-cheng,ShiShi-cai,etal.Asurveyofthespacesolararraytechnique[J].JournalofAstronautics,2014,35(5):491-498.]

[2] 王天舒,孔宪人,王本利,等.太阳帆板绳索联动同步机构的机理和功能分析[J].宇航学报,2000,21(3):29-33,38.[WangTian-shu,KongXian-ren,WangBen-li,etal.Theresearchonprincipleandfunctionofclosed-loopconfigurationofsolararrays[J].JournalofAstronautics,2000,21(3):29-33,38.]

[3] 马兴瑞, 王天舒,王本利,等.大型复杂航天器的柔性附件展开的动力学分析[J].中国空间科学技术,2000,8(4):1-7,14.[MaXing-rui,WangTian-shu,WangBen-li,etal.Dynamicsanalysisoflagerspacecraftwithdeployingflexibleappendages[J].ChinsesSpaceScienceandTechnology, 2000,8(4):1-7,14.]

[4] 李委托.太阳翼联动装置预置张力设计及分析[J].中国空间科学技术,2006,4(2):52-57.[LiWei-tuo.Thedesignandanalysesofclosecableloopofsolararray[J].ChinsesSpaceScienceandTechnology, 2006,4(2):52-57.]

[5] 宋顺广,王春洁.航天器附件联动展开机构优化设计[J].北京航空航天大学学报,2013,39(7):912-916.[SongShun-guang,WangChun-jie.Optimizationdesignofsynchronizationmechanismofspacecraftappendages[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013,39(7):912-916.]

[6]WieB，FurumotoN，BanerjeeAK，etal．Modelingandsimulationofspacecraftsolararraydeployment[J]．JournalofGuidance，ControlandDynamics，1986，9(5): 593-598.

[7]KumarP,PellegrinoS.Deploymentandretractionofacable-drivenrigidpanelsolararray[J].JournalofSpacecraftandRockets, 1996,33(6):836-842.

[8] 安源,谷松,金光.卫星太阳翼展开运动的分析及仿真[J].中国光学与应用光学,2009,2(1):29-35.[AnYuan,GuSong,JinGuang.Analysisandsimulationofdeploymentmotionofsatellitesolararray[J].ChineseJournalofOpticsandAppliedOptics, 2009,2(1):29-35.]

[9] 肖宁聪,李彦锋,黄洪钟.卫星太阳翼展开机构的可靠性分析方法研究[J].宇航学报,2009,30(4):1704-1710.[XiaoNing-cong,LiYan-feng,HuangHong-zhong.Reliabilityanalysismethodofdeploymentmecha-nismofasatellitesolararrays[J].JournalofAstronautics, 2009, 30(4):1704-1710.]

[10] 马尚君,刘更,罗浩.铰链展开式构型航天器设计及其动力学仿真[J].中国空间科学技术,2010,12(6):49-56.[MaShang-jun,LiuGeng,LuoHao.Designanddynamicsimulationofhingeddeployableconfigurationspacecraft[J].ChinsesSpaceScienceandTechnology, 2010,12(6):49-56.]

[11] 王晛,陈天智,柴洪友.太阳翼地面展开锁定的动力学仿真分析[J].航天器工程,2011,20(3):86-92.[WangXian,ChenTian-zhi,ChaiHong-you.Dynamicssimulationanalysisofsolararraygrounddeploymentandlocking[J].SpacecraftEngineering, 2011, 20(3):86-92.]

[12] 梁小光, 丁竹生, 焦映厚, 等.卫星太阳翼阻尼器参数选定方法[J].哈尔滨工业大学学报, 2011,43(7):71-75.[LiangXiao-guang,DingZhu-sheng,JiaoYing-hou,etal.Selectingmethodofdamperparametersforsolararrayofsatellite[J].JournalofHarbinInstituteofTechnology, 2011,43(7):71-75.]

[13] 罗浩,刘更,马尚君,等.齿轮齿条式构型航天器设计及其动力学仿真[J].系统仿真学报, 2012, 24(8):1606-1611,1617.[LuoHao,LiuGeng,MaShang-jun,etal.Designanddynamicsimulationofdeployablespacecraftdrivedbygearandrockmechanism[J].JournalofSystemSimulation, 2012, 24(8):1606-1611,1617.]

通信地址：上海市闵行区金都路3805号(201108)

电话：(021)24239101

E-mail:yangwenmiao2008@163.com

(编辑：牛苗苗)

Principle of CCL Synchronous Deployment and Dynamic Optimization of Solar Panel

YANG Wen-miao, SHI Jun-wei

(Shanghai Institute of Aerospace Systems Engineering, Shanghai 201108, China)

Based on the equivalent simplification of the closed cable loops (CCL), the principle of CCL synchronous deployment is analyzed and the mathematical model is established. The dynamic equation containing CCL is deduced in detail. Taking the synchronization analysis of a certain type of solar panels as an example, the dynamics of deployment and the cause of the large-scale non-synchronization are simulated and analyzed. The optimization model which is to minimize the asynchronous angle is set up and the parameters design of the driving torque is optimized by the sequential quadratic programming (SQP) algorithm. Compared with the traditional design method using the positive driving torque, the optimization results using the negative root driving torque parameters, reduce the loading of the linkage system effectively and improve the synchronous deployment of the solar panels.

Solar panels; Deployment dynamics; Optimization design; Sequential quadratic programming

2016-08-26;

2017-02-09

V423

A

1000-1328(2017)04-0338-06

10.3873/j.issn.1000-1328.2017.04.002

杨文淼(1983-)，男，博士，主要从事多体系统动力学与控制研究。