考虑柔性多体特征的复杂航天器分离动力学仿真分析
刘汉武,张 华,王金童,李东颖
(1. 上海宇航系统工程研究所,上海 201109;2上海市空间飞行器机构重点实验室,上海 201108)
考虑柔性多体特征的复杂航天器分离动力学仿真分析
刘汉武1,2,张 华1,2,王金童1,李东颖1,2
(1. 上海宇航系统工程研究所,上海 201109;2上海市空间飞行器机构重点实验室,上海 201108)
为了考察柔性多体特征对航天器分离姿态的影响,提出同时考虑太阳翼和分离舱的柔性,采用分离动力学及刚柔耦合动力学分析方法,建立航天器柔性多体动力学模型,通过航天器柔性多体分离动力学分析,解决了太阳翼和分离舱柔性特征对航天器分离姿态的影响问题,利用优化分析方法对航天器分离多参数影响进行了优化分析,得出了航天器分离姿态的极限情况,分析结果为弹簧分离机构的优化设计和分离安全性设计提供了理论参考,同时对空间站、载人航天、探月工程等国家重大项目的开展奠定了基础。
柔性多体;刚-柔耦合;分离动力学;设计优化
0 引 言
大型复杂航天器根据探测任务需要,其一次在轨飞行需满足的功能要求越来越多,尤其针对深空探测任务,航天器需满足轻量化、低成本、强约束等条件,这就要求很多航天器需在轨完成多次连接分离以开展各自的独立飞行任务。航天器分离过程涉及分离速度、姿态等众多动力学设计指标问题,关乎航天器探测任务成败,须进行充分验证和考核。由于地面试验手段的局限,难以模拟空间零重力状态下的航天器分离过程,仿真分析成为基本方法和必要手段[1-4]。目前大型复杂航天器在轨分离动力学的研究大都是将航天器和分离载荷简化假设为刚体,利用多刚体系统动力学进行分析,如付碧红[5]采用刚体多体动力学分析方法对搭载星与运载火箭分离过程进行了动力学分析;沈晓凤等[6]基于刚体多体动力学理论对小卫星筒式偏心分离动力学问题进行了仿真分析;丁庭山等[7]基于ADAMS软件平台采用多体动力学理论对小卫星及多星分离过程进行了模拟仿真;张华等[8]对两对接飞行器的分离过程和地面模拟试验过程进行了理论分析和仿真研究。美国、俄罗斯、法国等国家已经研制了相应的航天器平台或卫星平台,并进行了发射、分离方面的研究[9-11]。
上述这些研究均忽视了柔性附件对航天器分离的影响,袁瑞[12]研究了太阳帆板的柔性效应对轨道运动的影响和对姿态运动的影响,赵刚练等[13]利用多体动力学方法对考虑导轨间隙及碰撞因素的航天器分离过程进行了计算分析,发现导轨间隙使基座的转动与挠性附件强烈耦合,对航天器的稳定性造成了影响。这些研究均说明柔性附件对航天器分离姿态的影响不可忽视,但这些研究均没有考虑航天器本身的柔性对分离姿态的影响,随着航天器自身和柔性附件的刚度越来越低,同时对分离后航天器姿态控制的精度要求也越来越高,考察柔性多体特征对航天器分离姿态的影响显得越来越重要,而地面分离试验又无法完全避免地面重力和空气阻力等因素的影响,故需要对考虑柔性多体特征的航天器在轨分离过程进行仿真分析,为航天器在轨分离方案选择、分离参数的选取、航天器分离后姿态控制及分离安全性分析提供数据支撑,对空间站、载人航天、探月工程等国家重大项目的开展奠定了基础。
1 基础理论
1.1 分离动力学理论模型
航天器分离机构主要靠安装在对接框面的四根分离推杆提供动力将两连接的飞行器分离[8],其中每一根的推力都是独立作用在对接框面上,且沿x(负)方向(见图1)。
(1)
Fi是第i根推杆作用的推力,uxi(≤0)是第i根杆的端面在x方向的位移,F0、k分别为分离推杆的预紧力和弹性常数,s0是弹簧推杆的最大伸出长度。分离推杆作用在o点的力和力矩可简化为:
(2)
系统总动能
(3)
式中v为广义速度:
(4)
D为包含飞行器质量惯量特性及运动方向角的矩阵:
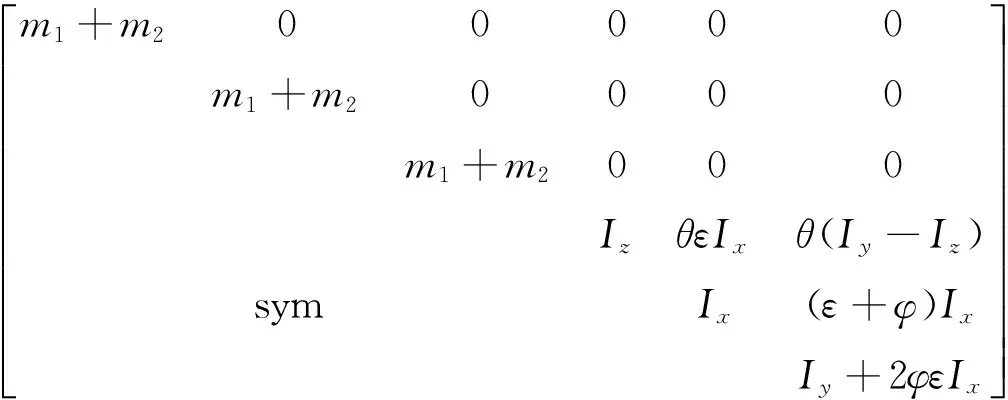
(5)
通过第二类拉格朗日方程
(6)
得到动力学方程:
(7)
其中
f=[4F04F0φ-4F0ψ000]T
(8)
(9)
(10)
式中:D为广义质量阵,C为阻尼,P为刚度系数。
1.2 刚体-柔体耦合动力学模型
刚体-柔体耦合动力学(简称刚柔耦合)的多体系统中的刚体按多刚体动力学理论建立方程,而柔性体用有限元法建立方程,将两者组集就可以得到刚柔耦合的多体系统动力学方程。首先对机械系统中的各个构件建立坐标系,进而获得整个多体系统中任意点的位置、速度和加速度,从而推导出系统中各个构件的动能、势能及广义力等参数,最终建立构件的动力学方程,最后将约束吸收到动力学方程中,形成整个多体系统的刚柔耦合模型。其中,多柔体系统的各构件的动力学方程可以由拉格朗日方程导出:
(11)
式中:L=T-W为拉格朗日项,T、W分别为系统的动能和势能,ψ=0是约束方程,Γ为系统的能量损耗函数,λ为对应于约束方程的拉格朗日乘子向量,ξ为广义坐标,Q为投影到广义坐标系的广义力。
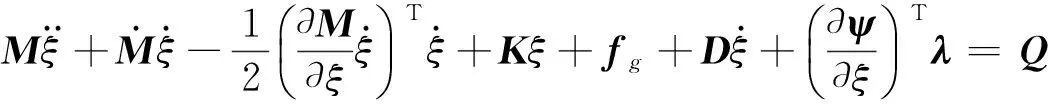
(12)
2 柔性多体动力学建模与分析
柔性体一般采用有限元法建模,其自由度较多,同时分析得出的模态频率也会很多,在结构动力分析中,普遍采用混合坐标法即用模态向量和相应的模态坐标来描述物体在空间随时间变化的位移(变形),即
uf=Φqη
(13)
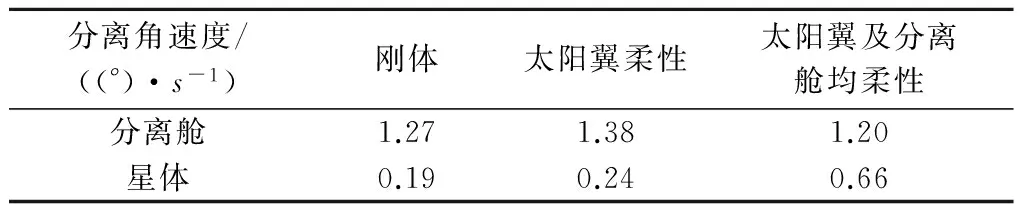
式中:Φ=[Φ1Φ2…ΦN]为模态向量矩阵,qη=qη(t)为模态坐标,N为模态向量数,通常选取N< 柔性体上节点的相对矢径与变形有如下的矢量关系式: (14) 节点k的绝对与相对矢径有如下的矢量关系式: rk=r+ρk (15) 节点k的绝对速度与加速度为: (16) (17) 通过式(14)~(17)可以计算出柔性体上各节点加速度,以及一系列运算可得柔性体广义惯性力和外力,从而得出其与航天器的耦合关系。要得到柔性附件与航天器的耦合关系,首先要得到柔性附件的模态参数。 2.1 柔性附件模型 太阳翼主要为航天器提供电能,是航天器不可或缺的一部分,同时也是最为典型的柔性附件,本文太阳翼结构为常见的蜂窝夹层结构,经过国内外学者的大量研究,太阳翼的柔性建模已趋于成熟。本文通过有限元方法建立太阳翼柔性模型,同时对太阳翼进行了模态分析,给出了前6阶模态频率、模态有效质量及主要振型(见表1)。表1中,TX:X方向平动;TY:Y方向平动;TZ:Z方向平动;RX:X方向转动;RY:Y方向转动;RZ:Z方向转动。 表1 太阳翼模态频率Table 1 The modal and frequency of solar wing 通过对太阳翼进行模态分析得出太阳翼的前30阶模态,其模态有效质量和已经达到90%以上,同时低阶的频率已经较大程度上反映了太阳翼的主要振型,故为了减少计算规模,本文在建立太阳翼柔性模型时截断前30阶频率。 2.2 柔性飞行器模型 分离舱载荷通过四点与星体连接,任务完成后需要进行分离,本文建立了分离舱的有限元模型(见图2),并对其进行了模态分析,得到前5阶的模态及前3阶振型(见表2和图2)。 序号频率/Hz121.50229.99345.76448.28549.97 与太阳翼柔性体建模一致,分离舱的前20阶模态的有效质量和已经达到90%以上,故截断分离舱前20阶频率,通过混合坐标法描述物体在空间随时间变化的位移。 3.1 柔性多体影响分析 太阳翼一阶频率为0.35Hz,为典型的低频柔性附件,同时航天器分离舱的一阶频率为21.5Hz,其频率较低,为分析分离舱的柔性对分离的影响,故而利用混合坐标法创建了太阳翼和航天器的柔性体模型,代入拉格朗日方程和运动学方程,建立了航天器分离的多柔体系统动力学模型(见图3)。由于星体频率高达80Hz,为分离舱频率的4倍,故而将星体简化为刚体。通过航天器多柔体系统分离动力学分析,分离过程中太阳翼根部耦合力及耦合力矩如图4~5所示,分离后星体和分离舱的分离速度及角速度如图6~9和表3所示。 由图6~9和表3可知,引入分离舱的柔性体模型的计算结果与刚体假设分析结果相比,分离舱的分离速度和分离角速度存在明显的震荡,这是与柔性体特征相符的,而太阳翼和分离舱柔性对分离后星体的速度几乎没有影响。从图9可以看出,引入太阳翼柔性后星体分离角速度的震荡幅度增大,与刚体计算结果相比分离角速度提高了26%,而引入分离舱柔性后星体分离角速度明显增大,与刚体计算结果相比分离角速度提高了247%,这是由于柔性太阳翼增大了星体的弹性,使得星体分离角速度震荡幅度变大,这与文献[12]中得出的结论是一致的,而由分离舱的弹性引起的弹簧力的偏差导致星体分离角速度明显增大。由此可知,在分离体刚度较低或柔性特性较明显的情况下,分离舱的柔性是不可忽视的,此时不能再按照刚体假设进行分离仿真计算,否则分析结果将与真实情况相差较大。同时分离舱的柔性和太阳翼的柔性增大了星体分离后的姿态变化,为星体的姿态控制增加了难度,只有使用精确的星体动力学模型,才能编写出有效的控制程序,在星体分离后快速控制姿态稳定。 分离角速度/((°)·s-1)刚体太阳翼柔性太阳翼及分离舱均柔性分离舱1.271.381.20星体0.190.240.66 3.2 覆盖性分析 航天器在分离过程中,有众多参数会影响航天器分离姿态,比如弹簧散差、星体质心偏差、弹簧作用线偏差、星体质量偏差、解锁不同步等,前期作者对这些参数对航天器分离姿态的影响进行了大量的研究分析,得出对航天器分离姿态三个主要的影响因素:弹簧散差、星体质心偏差、弹簧作用线偏差,本节基于具有柔性特征的航天器分离动力学模型,考虑影响分离姿态的三个主要参数,分析其对航天器分离姿态的影响。在航天器分离机构设计中需要对分离指标的覆盖性进行分析,这就需要得到各参数在容差变化范围内所能引起星体最恶劣的分离姿态。以前均采用经验和试算的方式寻求极限分离姿态,这在参数较少的情况下是可行的,但随着考虑的分离参数越来越多,各参数叠加的组合工况数量众多,若继续采用这种方式不仅费时费力,而且很难找到最恶劣工况,本文引入多参数优化分析方法来寻找航天器分离的最恶劣工况,设定这些参数的变化范围作为边界条件,以星体分离角速度进行最大值寻优,考察其是否满足分离姿态的指标要求。 经过优化分析,得到了星体最优角速度下各参数的取值(见图10~12)和最大分离角速度(见图13),此时最大分离角速度工况即为最恶劣工况,考察最恶劣分离姿态是否满足分离指标要求,为弹簧分离机构的优化设计和分离安全性设计提供参考。 引入了太阳翼和分离舱的柔性特征,建立了航天器柔性多体动力学模型,开展了航天器柔性多体分离动力学分析,分析结果表明: 1)太阳翼和分离舱柔性特征对航天器分离姿态具有显著影响,在分离舱频率较低的情况下,其柔性特征对分离动力学分析是不可忽视的,刚体假设不再适用。 2)基于柔性特征多体动力学模型考虑三个主要的分离参数(弹簧散差、星体质心偏差、弹簧作用线偏差)对航天器分离姿态的影响,通过多参数优化分析方法来寻找航天器分离的极限分离姿态,考察其是否满足分离姿态的指标要求。 3)研究成果为航天器在轨分离方案选择、分离参数的选取、航天器分离后姿态控制及分离安全性分析提供相关理论指导,对空间站、载人航天、探月工程等国家重大项目的开展奠定了基础。 [1]JeyakumarD,NageswaraRB.Dynamicsofsatelliteseparationsystem[J].JournalofSoundandVibration, 2006, 29(7): 444- 455. [2]MalyJR,HaskettSA,WilkePS.ESPA:EELVsecondarypayloadadapterwithwhole-spacecraftisolationforprimaryandsecondarypayloads[R].California,USA:SmartStructuresandMaterials:PassiveDampingandIsolation,April,2000. [3]ToorianA,BlundellE,SuariJP,etal.Cubesatsasresponsivesatellites[C].AIAA3rdResponsiveSpaceConference,USA,April,2005. [4]LeeYJ,KangWK,KimDJ.Modelingandsimulationofashapememoryreleasedevice[R].ProceedingsofAsianJointConferenceonPropulsionandPower,Beijing,China,April20-23,2006. [5] 付碧红. 搭载星与运载火箭分离的动力学研究[J].飞行力学,2006, 24(1):55-58. [FuBi-hong.Separationdynamicsprocessofpiggybacksatellitefromlaunchvehicle[J].FlightDynamics, 2006, 24(1):55-58.] [6] 沈晓凤,肖余之,康志宇. 小卫星偏心分离动力学仿真模型的建立与验证[J].飞行力学,2012,30(3):258-262.[ShenXiao-feng,XiaoYu-zhi,KangZhi-yu.Establishmentandvalidationondynamicssimulationmodelofseparationofeccentricsub-satellite[J].FlightDynamics, 2012, 30(3):258-262.] [7] 丁庭山,孟宪红. 多星二次分离的仿真研究[C]. 探索 创新 交流(第4集)2010年第四届中国航空学会青年科技论坛文集,北京,中国,2010年11月25-26.[DingTing-shan,MengXian-hong.Simulationofthemulti-satelliteseparation[C].TheFourthAviationInstituteYouthScienceandTechnologyBBSCorpus,Beijing,China,November25-26, 2010.] [8] 张华,肖余之,徐博侯,等.空间飞行器的对接分离与地面模拟试验的仿真分析研究[J].宇航学报,2008,29(6):1761-1765.[ZhangHua,XiaoYu-zhi,XuBo-hou,etal.Analysisstudyonseparationofaerospacevehicleandgroundsimulationtest[J].JournalofAstronautics, 2008,29(6):1761- 1765.] [9]MartiSK,NesrinSK,HudsonGC,etal.Gravityairlaunchingofearth-to-orbitspacevehicles[R].AIAA2006-7256,2006. [10]SandauR.Statusandtrendsofsmallsatellitemissionsforearthobservation[J].ActaAstronautica,2010,66(1-2):1-12. [11]RogersAQ,PaxtonLJ.Smallsatelliteconstellationsformeasurementsofthenear-earthspaceenvironment[C].DigestoftheSeventhInternationalSymposiumoftheIAA,WissenschaftundTechnikVerlag,Berlin,Germany,May,2009. [12] 袁瑞. 航天器轨道机动动力学和分离动力学研究[D].上海:上海交通大学,2009.[YuanRui.Investigationontheorbitmaneuverdynamicsandseparationdynamicsofspacecrafts[D].Shanghai:ShanghaiJiaoTongUniversity, 2009.] [13] 赵刚练,姜毅.考虑导轨间隙的在轨分离动力学计算方法[J].力学学报,2013,45(6):948-956.[ZhaoGang-lian,JiangYi.Computationalmethodfordynamicssimulationofpayloadseparationfromsatellitewithrailclearance[J].ChineseJournalofTheoreticalandAppliedMechanics,2013,45(6):948-956.] 通信地址:上海市闵行区元江路3888号805所(201109) 电话:18721986520 E-mail:jingxi105@163.com (编辑:牛苗苗) Simulation Analysis of Complex Spacecraft Separation Dynamics Considering Characteristics of Flexible Multi-Body LIU Han-wu1,2, ZHANG Hua1,2, WANG Jin-tong1, LI Dong-ying1,2 (1. Shanghai Institute of Aerospace Systems Engineering, Shanghai 201109, China;2. Shanghai Key Laboratory of Spacecraft Mechanism, Shanghai 201108, China) In order to study the influence of the characteristics of the flexible multi-body spacecraft on its separating attitude, this paper considers the flexibility of the solar wing and the separation module and uses the separation dynamics and the rigid-flexible coupled dynamics analysis method to establish the spacecraft flexible multi-body dynamics model. Through the spacecraft flexible multi-body separation dynamics analysis, the influence of the flexible characteristics of the solar wing and the separation module on the spacecraft separation attitude can be solved. By using the method of optimization analysis to optimize and analyze the multi-parameter influence on the spacecraft separation, the limits of the spacecraft separation attitude can be obtained. The analysis results provide the theoretical reference for optimal design and separation safety of the spring separation mechanism, while laying a foundation for carrying out the national key programs such as space station, manned spaceflight, lunar exploration. Flexible muti-body; Rrigid-flexible coupling; Separation dynamics; Design optimization 2016-09-22; 2017-01-24 国家高性能计算重点基金(2016YFB0201604);上海市自然科学基金(16ZR1436200) TP731 A 1000-1328(2017)04-0352-07 10.3873/j.issn.1000-1328.2017.04.004 刘汉武(1986-),男,硕士,主要从事结构和机构动力学仿真分析研究。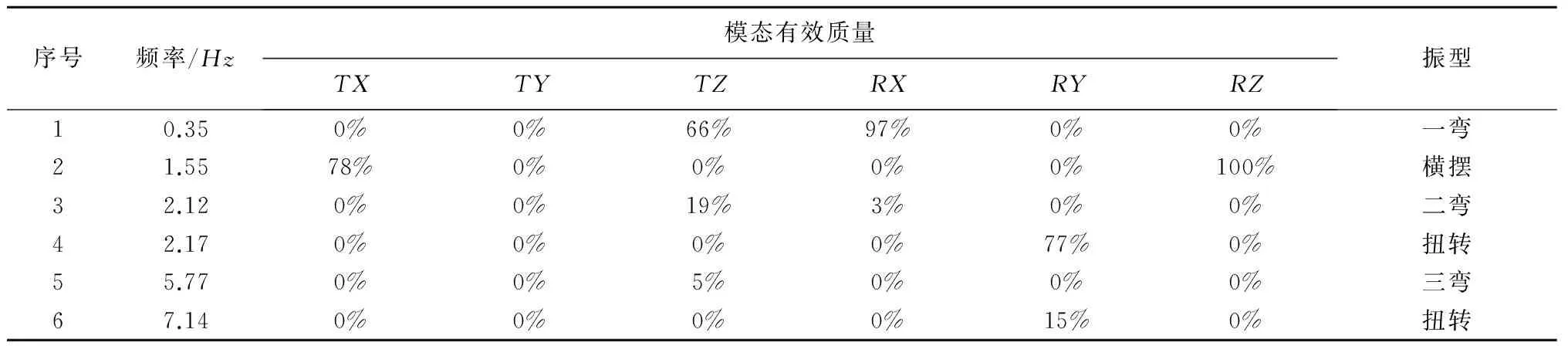

3 分离仿真分析
4 结束语

