载人登月绕月自由返回轨道混合-分层优化设计
曹鹏飞,贺波勇,彭祺擘,李海阳
(1. 国防科学技术大学航天科学与工程学院,长沙410073;2. 载人航天总体研究论证中心,北京100094)
载人登月绕月自由返回轨道混合-分层优化设计
曹鹏飞1,贺波勇1,彭祺擘2,李海阳1
(1. 国防科学技术大学航天科学与工程学院,长沙410073;2. 载人航天总体研究论证中心,北京100094)
针对载人登月绕月自由返回飞行任务,提出一种混合-分层轨道优化设计方法。将高精度模型下强约束自由返回轨道设计问题转化为有约束非线性规划求解问题,在此基础上提出一种混合-分层优化求解策略。在双二体模型下利用差分进化算法(DE)与序列二次规划(SQP)相结合的混合优化算法快速求解了满足弱约束条件下的轨道初值问题。采用序列二次规划(SQP)构造两层迭代格式,在高精度模型和强目标约束下对初步设计轨道进行逐层修正。最后,通过仿真测试,文章所述方法的可行性与有效性得到了验证。仿真飞行结果还进一步表明该设计方法具有求解精度高、收敛速度快等优点,为探月工程任务提供了一种有效的轨道设计工具。
载人登月;绕月自由返回飞行;轨道设计;混合-分层优化
0 引 言
月球是地球唯一的天然卫星,是人类进入深空最理想的中转站,因而人类从未放弃对月球的探索[1]。1969年7月16日,美国成功发射了Apollo 11号飞船,实现了人类历史上的首次载人登月。2004年,美国启动了重返月球的“星座计划”,提出了全月面到达和任意时刻安全返回等新时期载人登月任务目标[2],后由于财政等诸多原因这一计划被奥巴马终止。伴随着“星座计划”的提出,国际上掀起了新一轮月球探测热潮,美、俄、欧空局、中、日和印度都制定了探月计划。作为载人登月关键技术之一的轨道设计,一直是该领域的研究热点。与无人探测不同,载人登月轨道要保证航天员的安全,即必须具有任务各个阶段发生故障时任务中止和航天员安全返回的能力[3]。绕月自由返回轨道(简称自由返回轨道)作为由近地停泊轨道(Low Earth orbit, LEO)出发,经月球近旁转向,之后返回地球的轨道(见图1),具有很高的安全性,在登月史上被广泛应用。值得关注的是,Apollo 13号飞船在发生故障后加速进入一条自由返回轨道,绕月后返回地球,成功挽救了航天员的生命。
自由返回轨道早期研究主要是用于载人登月及相关试验任务,使用的动力学模型比较简单如双二体模型、圆型限制性三体模型(Circular restricted three-body problem, CR3BP)等,主要用于轨道解析或半解析求解和特性分析等。Miele[4]基于圆型限制性三体模型证明了地月空间镜像轨道的存在,并于2010年,采用镜像轨道理论重新定义了镜像轨道和对称自由返回轨道[5]。Penzo[6]和Gibson[7]通过双二体模型假设和圆锥曲线拼接法研究了自由返回轨道原理特性。Jesick等[8]基于圆型限制性三体模型和微分校正策略求解了满足近月点高度和再入角约束的自由返回轨道。国内较早由郗晓宁等[9]提出了一种由简单模型到复杂模型、由初步设计到精确修正的自由返回轨道分层设计方法,影响较广。白玉铸等[10]将月地转移段作为应急返回使用,只对近地点高度约束,采用分段受摄的高精度模型和微分修正求解了自由返回轨道,精度高但存在约束弱等局限。黄文德等[11]基于双二体模型求解了自由返回轨道,适用于特性分析。张磊等[12]在双二体模型下采用圆锥曲线拼接法完成了自由返回轨道的初步设计,后通过三级微分修正完成了轨道高精度模型下求解,精度高但过程复杂。Peng等[13]采用全局优化的粒子群算法(Particle swarm optimization, PSO)和局部寻优的序列二次规划(Sequence quadratic program, SQP)对自由返回轨道进行分步设计,前一步结果作为后一步迭代初值,精度高但计算效率低,且易出现初值陷入局部最优导致高精度修正不收敛的情况。Li等[14]综合了Hybrid轨道与自由返回轨道的优点,提出了多段自由返回轨道概念,继承了自由返回轨道安全和Hybrid轨道发射窗口与着月范围较宽的优点,但燃料消耗量太大,距离工程使用尚有一定距离,且中途变轨后进入的低近月心距轨道并不属于严格意义上的自由返回轨道。贺波勇等[15]和贺波勇等[16]在研究了载人登月转移轨道偏差传播机理后提出由近月点出发逆/正高精度数值积分求解自由返回轨道的思路,并在此基础上构造了初值求取和高精度修正的串行求解算法,有效降低了绕月引力辅助甩摆段强非线性的影响,但计算效率较低且存在局限性,即逆/正向求解的轨道在正向验证时,近月点和真空近地点[17](图1中R点)处的高度与目标值仍存在一定偏差。这是由算法修正不彻底和入轨点对偏差比较敏感[18]导致。
针对载人登月绕月自由返回轨道设计问题,文献[16]提出的求解思路具有重要的参考意义,本文则进一步提出了高精度分层SQP修正的求解方法。将高精度模型下强约束自由返回轨道设计问题转化为有约束非线性规划求解问题,在此基础上提出一种混合-分层优化求解策略。在双二体模型下利用差分进化算法(Differentialevolution,DE)与SQP相结合的混合优化算法快速求解满足弱约束条件下的轨道初值问题。采用SQP构造两层迭代格式,在高精度模型和强目标约束下对初步设计轨道进行逐层修正。通过仿真测试,文章所述方法的可行性与有效性得到验证,仿真结果还进一步表明该设计方法具有求解精度高、收敛速度快等优点。
1 动力学模型和约束
载人登月任务背景复杂、工程约束苛刻,轨道求解精度要求严格,传统的二体模型、双二体模型和限制性三体模型等难以满足,因此必须考虑引入各种摄动加速度的高精度模型。
1.1 高精度模型
在地心J2000坐标系下,考虑地球中心引力、日月引力摄动、地球和月球非球形引力摄动以及太阳光压摄动,大气阻力摄动等,探测器轨道动力学方程如下所示
(1)
式中:r为地心位置矢量;μE为地球引力常数;AN为N体引力摄动加速度,星体间空间几何关系通过DE405/LE405星历求解;ANSE为地球非球形摄动,取WGS84引力场模型8×8阶计算;ANSM为月球非球形摄动,取LP165P引力场模型8×8阶计算;AR为太阳光压摄动;AD为大气阻力摄动加速度;AP为推进加速度。这里忽略地球潮汐、相对论效应和其他微小摄动量的影响。
1.2 约束
与无人任务相比,载人登月任务包含一系列的复杂约束条件,可分为工程约束与轨道约束。工程约束主要包括飞行时间、速度增量和月面阳光入射角约束。为保证航天员的安全,一般要求地月转移时间t1与月地转移时间t2不能太长;受飞行器运载能力限制,发动机所能提供的速度冲量(包括入轨点速度冲量ΔvE和近月点制动速度冲量ΔvC)有限;此外考虑到测控方面的限制,着陆时对月面阳光入射角Θsun也有要求。本文将工程约束简化为
(2)
轨道约束包括地心段轨道、月心段轨道和返回轨道约束。以典型的“Apollo”式自由返回轨道为例,轨道约束可简化为
(3)
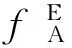
2 自由返回轨道设计
本文将高精度模型下的强约束自由返回轨道设计问题转化为有约束非线性规划求解问题,提出了一种由初值搜索到高精度修正的混合-分层求解策略,流程如图3所示。
2.1 初值搜索
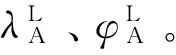
(4)
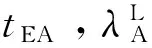
minf(x)=ΔvE+ΔvC
(5)
为避免初值陷入局部最优和提高搜索效率,本文采取以下措施:1)选用全局搜索能力较强的差分进化算法和局部优化效率较高的SQP相结合的混合优化算法求解初值;2)参考文献[11]自由返回轨道特性分析结果设置搜索变量区间。
2.2 高精度分层修正
高精度分层修正阶段,本文基于高精度模型采用数值积分求解。引入近月点坐标系[16]Om-xPyPzP,其中,原点Om为位于月球质心,xP轴指向轨道近月点,zP轴指向轨道面反法向,yP轴与其他两轴构成右手系。在Om-xPyPzP坐标系下定义:rP、vP为探测器位于近月点处的位置、速度矢量,rP、vP为对应矢量的模,iP为轨道伪倾角即vP与yP轴正方向的夹角。下式为给出了瞬时月心白道坐标系到近月点坐标系的转换矩阵计算式
M=M2(β)M3(α)
(6)
式中:α和β为表征近月点位置矢量的方位角[16]。
在高精度模型和强目标约束下,采用分层SQP修正策略对初值进行逐层修正。为降低绕月引力辅助甩摆段强非线性对轨道求解精度的影响,第一层SQP修正时,采用文献[16]的求解思路,即以近月点为界将自由返回轨道分为地月转移和月地转移两段,分别进行逆向和正向积分求解。为消除逆向求解产生的偏差,需进行第二层SQP修正,采用以入轨点出发正向积分的求解思路。在即保证计算效率同时又不损失求解精度的情况下提出假设:探测器从入轨点到近月点的时间和从近月点到真空近地点的时间,在第二层SQP修正前后保持不变。详细求解流程如图5所示。
第一层:快速修正初步设计以得到满足入轨点高度约束和轨道倾角约束的过渡轨道。以α、β、vP、iP为优化变量,迭代初值取自初步设计,采用文献[16]轨道精确优化方法和龙格库塔4阶(RK4)定步长积分器,快速生成精度不高但优于初步设计的过渡轨道,近月点时刻tTLI和rP由初步设计确定。为降低收敛难度,将等式约束处理成目标函数
(7)
第二层:快速修正过渡轨道以得到满足所有约束的精确轨道。以入轨时刻过渡轨道地心段偏心率e、升交点赤经Ω和近心点角距ω为优化变量,采用正向积分求解思路和龙格库塔4-5阶(RKF45)变步长积分器,快速收敛至满足所有约束的精确轨道。入轨时刻tTEI、入轨点真近点角fE、rE、iE由过渡轨道确定。将等式约束处理成目标函数
(8)
3 仿真校验
给出自由返回轨道设计实例,约束参数设置如下:入轨点高度hE为200km,近月点高度hP为122.09km,真空近地点高度hreen为54km,地心段轨道倾角iE为20°,入轨点速度冲量倾角ΘE为0°。入轨时刻约为3Jan2025 05:40:0.000UTCG,约3天后抵达近月点。仿真在计算机CPU为2.67GHz的VC++6.0环境下进行。
首先,根据计算流程图4对自由返回轨道进行初步设计。设计变量的寻优结果和约束条件满足情况如表1所示,近月点的时刻为5Jan2025 23: 44: 4.759UTCG。

表1 初步搜索优化变量最优解和约束条件满足情况Table 1 Optimal values of the optimization variables in preliminary searching and conformance of the constraint conditions
采用文献[16]提出的轨道高精度精确优化方法,对初步设计轨道进行修正。为保证求解精度,最大迭代次数设为100,积分步长设为1s,迭代初值取自初步设计轨道如表2所示,修正得到的轨道称为文献轨道。轨道入轨点修正轨道根数如表3所示,入轨时刻为3Jan2025 05:55: 38.259UTCG,计算时长和约束条件满足情况如表4所示。

表2 高精度第一层SQP修正时的优化变量初值Table 2 Initial values of the optimization variables for the first SQP optimization under high precise model

表3 轨道入轨点修正轨道根数Table 3 Modified classical orbit elements of trans-lunar injection points
采用本文提出的高精度分层SQP修正方法和图5的计算流程,对初步设计轨道进行分层修正。第一层SQP修正时,最大迭代次数设为100,积分步长设为T,迭代初值取自初步设计轨道如表2所示,修正得到过渡轨道;第二层SQP修正时,最大迭代次数设为100,积分精度设为10-13,迭代初值取自过渡轨道,修正得到精确轨道。表3给出了T取5s时,过渡轨道和精确轨道的修正轨道根数,入轨时刻均为3 Jan 2025 05: 58: 37.259 UTCG,用商业软件STK11验证精确轨道空间轨迹如图6所示。
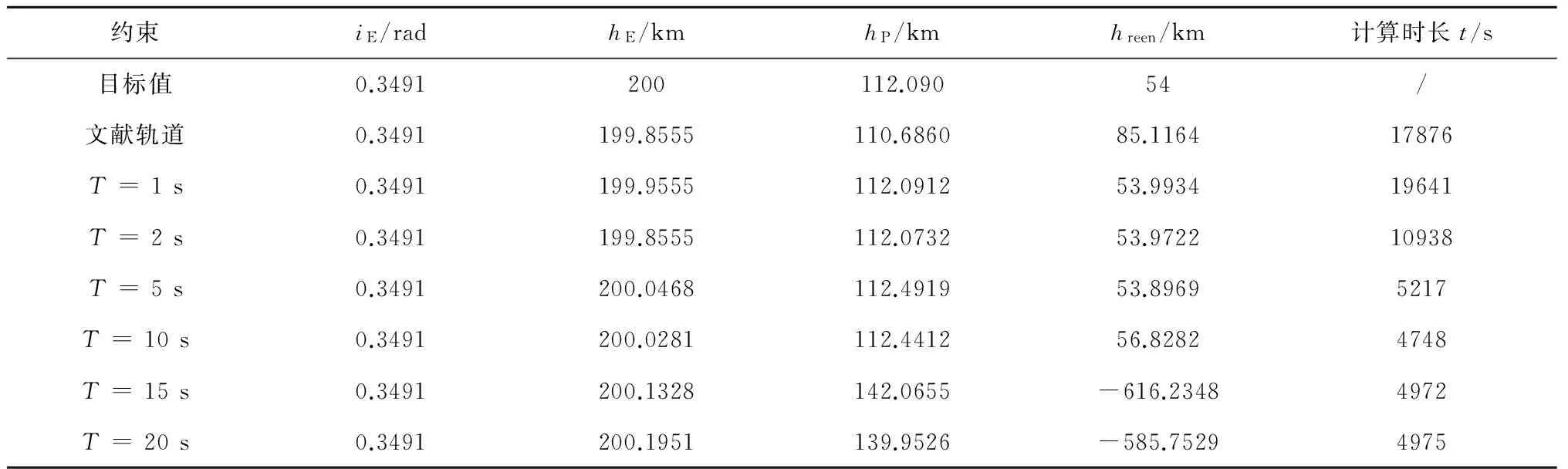
表4 求解精度和计算时长随积分步长T的变化情况Table 4 Change with the integration step T of the computation time and solution accuracy
仿真发现,第一层SQP修正时的积分步长T是影响分层SQP修正方法求解精度和效率的重要参数。表4给出了T取不同值时求解精度和计算时长的变化情况,表中高度信息由STK11正向分段递推得到,终止条件为近月点和真空近地点。
由表4可知:1)随着T的增大,轨道倾角iE和近地点高度hE在目标值附近波动,说明第一层SQP修正能高效地修正轨道倾角与近地点高度。2)T越小,分层SQP修正的求解精度越高,但计算时长却大大增加,特别地,当T= 1s时,轨道在高度约束处的值与目标值相差均在百米以内,精度远高于文献解。3)当T大于10s时,分层SQP修正的求解精度和效率有所降低,原因是T过大致使第二层SQP修正时迭代初值不准导致收敛速度慢和精度下降。4)综合考虑求解精度与效率,在使用分层SQP修正方法时,推荐T取5s。
为了不失一般性,独立地改变轨道在近地点、近月点和真空近地点处的高度约束,其余参数保持不变,分别采用文献[16]方法和分层SQP修正方法进行求解,结果如表5所示。对比两种方法的求解精度和效率,发现分层SQP修正方法在高精度强约束自由返回轨道求解方面具有求解精度高和计算速度快等优点。
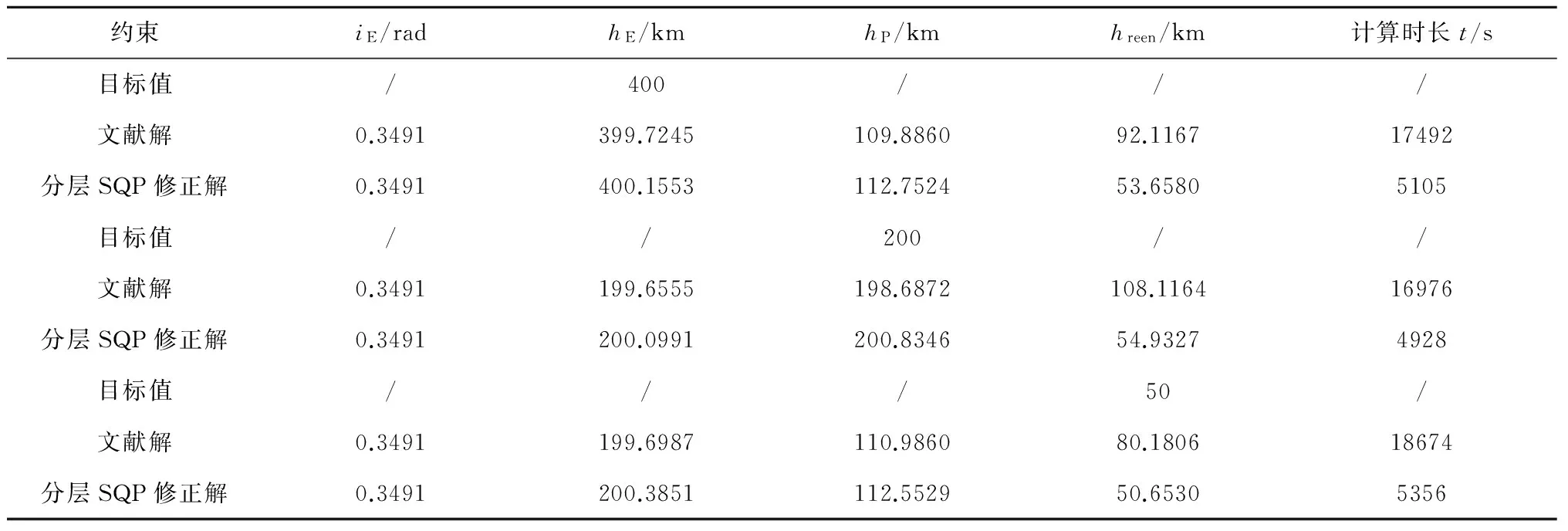
表5 给定T = 5s,不同约束条件下分层SQP修正方法的求解精度和计算时长Table 5 Solution accuracy and computation time of two-level SQP optimization under different constraint conditions when T=5s
4 结 论
针对载人登月绕月自由返回飞行任务,提出一种轨道设计方法。将高精度模型下强约束自由返回轨道设计问题转化为有约束非线性规划求解问题,在此基础上提出了一种混合-分层优化求解策略。在双二体模型下利用差分进化算法与SQP相结合的混合优化算法快速求解了满足弱约束条件下的轨道初值问题。采用SQP构造两层迭代格式,在高精度模型和强目标约束下对初步设计轨道进行逐层修正。仿真实例表明,文中分层SQP修正方法能高效地完成复杂约束下的绕月自由返回轨道高精度模型设计任务,仿真结果还进一步表明了该设计方法具有求解精度高、收敛速度快等优点。
[1] 龙乐豪, 容易. 现代“嫦娥奔月”的技术途径设想 [J]. 导弹与航天运载技术, 2008, 293(1): 1-7. [Long Le-hao, Rong Yi. Research on the technical approach of manned lunar mission [J]. Missiles and Space Vehicles, 2008, 293(1): 1-7.]
[2] Garn M, Qu M, Chrone J, et al. NASA′s planned return to the moon: global access and anytime return requirement implications on the lunar orbit insertion burns [C]. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, AIAA 2008-7508, 2008.
[3] Xi X N, Huang W D, Wang W, et al. Review on abort trajectory for manned lunar landing mission [J]. Science China Technology Sciences, 2010, 53(10): 2691-2698.
[4] Miele A. Theorem of image trajectories in Earth Moon space [J]. Acta Astronaut, 1960, 6(5): 225-232.
[5] Miele A. Revisit of the theorem of image trajectories in the Earth-Moon space [J]. Journal of Optimization Theory and Applications, 2010, 147(3): 483-490.
[6] Penzo A P. An analysis of free-flight circumlunar trajectories [C]. AIAA Astrodynamics Conference, New Haven, USA, August 19-21, 1963.
[7] Gibson F T. Application of matched conic model in the study of circumlunar trajectories [R]. NASA Project Apollo Working Paper No.1066, February, 1963.
[8] Jesick M, Ocampo C. Automated generation of symmetric lunar free-return trajectories [J]. Journal of Guidance, Control, and Dynamics, 2015, 34(1): 98-106.
[9] 郗晓宁, 曾国强, 任萱, 等. 月球探测器轨道设计 [M]. 北京: 国防工业出版社, 2001.
[10] 白玉铸, 陈小前, 李京浩. 载人登月自由返回轨道与Hybrid轨道设计方法 [J]. 国防科技大学学报, 2010, 32(2): 33-39. [Bai Yu-zhu, Chen Xiao-qian, Li Jing-hao. Free-return trajectory and hybrid trajectory design for manned lunar landing missions [J]. Journal of National University of Defense Technology, 2010, 32(2): 33-39.]
[11] 黄文德, 郗晓宁, 王威, 等. 基于双二体假设的载人登月自由返回轨道特性分析及设计 [J]. 宇航学报, 2010, 31(5): 1297-1303. [Hang Wen-de, Xi Xiao-ning, Wang Wei, et al. Characteristic analysis and design of free return orbit for lunar manned landing based on the double two-body model [J]. Journal of Astronautics, 2010, 31(5): 1297-1303.]
[12] 张磊, 谢剑锋, 唐歌实. 绕月自由返回飞行任务的轨道设计方法 [J]. 宇航学报, 2014, 35(12): 1388-1394. [Zhang Lei, Xie Jian-feng, Tang Ge-shi. Method of mission trajectory design for circumlunar free return flight [J]. Journal of Astronautics, 2014, 35(12): 1388-1394.]
[13] Peng Q B, Shen H X, Li H Y, et al. Free return orbit design and characteristics analysis for manned lunar mission [J]. Sci. China Tech Sci., 2011, 54(12): 3243-3250.
[14] Li J Y, Gong S P, Baoyin H X, et al. Generation of multisegment lunar free-return trajectories [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(3): 765-775.
[15] 贺波勇, 李海阳, 张波. 载人登月转移轨道偏差传播机理分析与稳健性设计 [J]. 物理学报, 2013, 62(19): 91-98. [He Bo-yong, Li Hai-yang, Zhang Bo. Analysis of transfer orbit deviation propagation mechanism and robust design for manned lunar landing [J]. Acta Physica Sinica, 2013, 62(19): 91-98.]
[16] 贺波勇, 李海阳, 周建平. 载人登月绕月自由返回轨道与窗口精确快速设计 [J]. 宇航学报, 2016, 37(5): 512-518. [He Bo-yong, Li Hai-yang, Zhou Jian-ping. Rapid design of circumlunar free-return high accuracy trajectory and trans-lunar window for manned lunar landing mission [J]. Journal of Astronautics, 2016, 37(5): 512-518.]
[17] Shen H X, Zhou J P, Peng Q B, et al. Point return orbit design and characteristics analysis for manned lunar mission [J]. Sci. China Tech. Sci., 2012, 55(9): 2561-2569.
[18] 周文艳, 杨维廉. 月球探测器转移轨道的中途修正 [J]. 宇航学报, 2004, 25 (1): 89-92. [Zhou Wen-yan, Yang Wei-lian. Mid-correction of trans-lunar trajectory of lunar explorer [J]. Journal of Astronautics, 2004, 25 (1): 89-92.]
[19] 贺波勇, 彭祺擘, 沈红新, 等. 载人登月轨道月面可达域分析 [J]. 载人航天, 2014, 20(4): 290-295. [He Bo-yong, Peng Qi-bo, Shen Hong-xin, et al. Capable region analysis of orbit for manned lunar landing mission [J]. Manned Spaceflight, 2014, 20(4): 290-295.]
通信地址:湖南长沙开福区德雅路109号航天科学与工程学院A314(410073)
电话:13015509011
E-mail: caopengfei_nudt@163.com
(编辑:牛苗苗)
Hybrid and Two-Level Optimization Design of Circumlunar Free-Return Trajectory for Manned Lunar Landing Mission
CAO Peng-fei1, HE Bo-yong1, PENG Qi-bo2, LI Hai-yang1
(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China; 2. Manned Space System Research Center, Beijing 100094, China)
An optimization method of trajectory design is established in this paper for manned lunar landing circumlunar free-return flight mission. The problem of designing free-return trajectory with multiple constrains under the high precise dynamic model is converted to the nonlinear bounded optimization problems. A solving strategy consisting of hybrid and two-level optimization algorithm is then proposed. Under the double two-body model, the initial trajectory with the weak constrain conditions is obtained by hybrid optimization algorithm which consists of differential evolution (DE) method and sequence quadratic program (SQP) method based on the patched-conic approach. Then a two-level initial trajectory corrective measure based on the sequence quadratic program is applied to obtain the final solution satisfying the strong engineering constrains under the high precise dynamic model. Finally, the reliability and effectiveness of the approach proposed in this paper are demonstrated by the simulation tests, and the results indicate that the proposed method has excellent convergence performance and high precision, thus can be a useful tool for manned lunar orbit design.
Manned lunar landing; Circumlunar free-return flight; Trajectory design; Hybrid and two-level optimization
2016-11-17;
2017-02-12
国家自然科学基金(11372345);国家重点基础研究发展计划(973计划)(2013CB733100)
V412.4
A
1000-1328(2017)04-0331-07
10.3873/j.issn.1000-1328.2017.04.001
曹鹏飞(1992-),男,硕士生,主要从事月球及深空探测技术研究。

