大气湍流对平流层星光导航中星光传输的影响

杨 博，朱雪妍

(北京航空航天大学宇航学院，北京100191)

大气湍流对平流层星光导航中星光传输的影响

杨 博，朱雪妍

(北京航空航天大学宇航学院，北京100191)

以平流层飞行器用星光导航为背景，研究在平流层内星光传输过程受大气湍流的影响机理，揭示平流层中星光的衰减规律，为建立平流层星光导航星库以及电耦合器件(CCD)所摄取的星图补偿方法提供理论依据。研究提出将流场密度和流场密度脉动变化大的区域划分为宽度为L的特性截面，并基于几何光学法及统计光学理论分别计算星光穿过各特性截面后产生的光线偏折及平均光强衰减，进而推导整个平流层内星光传输过程中的能量衰减变化曲线。采用基于k-ε双方程湍流模型的雷诺平均法计算不同极端情况下的大气湍流场密度及密度脉动分布。通过计算机数值仿真表明：星光穿过具有湍流的平流层时将发生明显偏折，其偏折程度与流场密度值有关；同时星光光强衰减，衰减程度与流场密度脉动值有关。

星光导航；大气湍流；大气光学效应；星等

0 引 言

近年来随着各国航天技术的飞速发展，平流层空间的战略价值越来越受到各国的重视。平流层飞行器因其显著特点和潜在的军、民两用价值而成为各国研究的热点。平流层飞行器能在平流层内长时间运行，而不受地面因素限制的自主导航技术是该领域研究的重要关键技术之一。

星光导航是一种完全自主的导航技术，天体的空间运动规律不受人为改变,使其抗干扰能力强,具有最完备的可靠性，同时适用范围广 ,不受地域、空域和时域的限制,是一种在宇宙空间内处处适用的导航技术[1]。因此，研究平流层自主星光导航技术有其重要的理论价值和军事应用价值。

星光穿过平流层大气时会碰到随机性很强的大气湍流，因而在传输过程中受到不均匀大气折射的干扰，衍生出一系列如光束抖动等大气湍流效应，严重影响平流层大气环境下星光导航系统的性能以及导航星库的准确建立[2-8]。因而研究平流层大气湍流效应对星光传输的影响机理是实现平流层星光导航技术的基础。目前国内外均采用不同统计特性的相位屏模拟大气湍流的方法。该相位屏产生方法分为两类[9]:一是“功率谱反演法”，是对频率域间接模拟；二是“Zernike 多项式展开法”，是对空间域的直接模拟。其都是单纯的从光学成像结果中分析大气湍流对光线造成的扰动，而无法揭示星光穿过大气湍流场过程中引起的传输误差和能量衰减变化机理。

文中对考虑了平流层气溶胶粒子和水汽等自然环境条件的大气湍流进行模拟。通过光线追迹法及平均光强推导平流层内星光传输过程中的能量衰减规律，深入研究星光在大气湍流流场中的传输特性。

1 平流层大气湍流场的数值模拟

在湍流大气中，折射率随时间和空间的起伏变化需具备一定的动力学和热力学条件：前者是空气层中有明显的风速切变；后者则是空气层有一定的不稳定度，其中最有利的是上层空气温度低于下层的对流条件[10]。以此为基础，采用k-ε双方程湍流模型对考虑气溶胶粒子和水汽等自然环境条件的平流层大气湍流流场进行模拟。

雷诺平均方程组为：

(1)

(2)式中

其中，σk=1.0,σε=1.3,c1=1.44,c2=1.92,cμ=0.09，参数E、F、G、R、S、T、Lk、Lε、Pk的定义详见文献 [11]。

2 光线追迹法求流场中星光偏折

星光通过折射率变化的湍流大气时不断发生折射，即散射效应。采用光线追迹法模拟星光在湍流场中的传输路径，并用星点质心的偏移量描述星光在湍流场中传输的偏折程度。

2.1 Runge-Kutta法解算星光传输方程

由Hamilton光学中的Lagrange方程整理可得星光光线传输方程矢量形式如下：

d(n(r)dr/ds)/ds=▽n(r)

(3)

式中：r=xi+yj+zk,为光线上某点的位置坐标，n(r)为折射率分布，ds为沿光线的弧元。

为便于积分，作如下定义：

由此将式(3)整合为：

(4)

定义三个矩阵:

将式(4)写成矩阵形式为：

d2R/dt2=D(R)

(5)

式中:D(R) 为位置矢量R的矢量函数，给定R0(x0,y0,z0)及T0(T0x,T0y,T0z)。根据Runge-Kutta方法进行数值积分，得到追迹光线通过媒介的计算式为[12]：

(6)

式中：

其中，Δt是t的增量，其值由折射率分布及精度要求确定。

2.2 流场中星光传输的偏折计算

根据Gladstone-Dale定律，介质的密度ρ与折射率n的关系为：

(7)

式中：ρ是气体密度，ρ0是标准状态下的气体密度，KGD为空气折射率的Gladstone-Dale系数，简称G-D系数。由经验式获得：

(8)

式中：λ为光波波长，单位μm；KGD的单位为cm3/g。

通过式(8)将流场的密度分布转换为折射率分布，用于研究星光在流场介质中的传输。

光波在流场中传输的位置关系如图1所示，假设光轴(法线)方向是垂直于探测窗口平面的负向，nij表示划分网格后的湍流密度场第i行第j列方格内的流体折射率，d为网格单元大小。

图1中，设光线初始入射角为θ0，折射节点2、3之间折射率为n11，光线通过节点2后折射角为θ1，第i行j列的方格内折射率为nij；当第k次折射时对应折射角为θk，设第k个折变点对应坐标为(X,Z)。令ΔXk表示光线平移量(X轴偏差量)，即ΔXk=Xk-Xk-1。

在光线折射点k处，由Snell折射定律得到关系式：

(9)

令∑kΔXk表示光线的总偏移量。由图1三角关系易得：

M=d(∑kΔXk-ld)/ΔXk

(10)

式中：M、d见图1。

对式(9)修正得光线的总偏移量为：

(11)

由式(11)可得到星光穿过湍流流场后总的星点质心偏移量,即总的偏折程度。

3 统计光学法求湍流中星光能耗

星光通过湍流大气时由于散射效应能量被严重衰减，致使导航星等降低。在湍流流场中密度变化较剧烈的层间边界处取一定厚度为L的截面，利用统计光学理论计算各截面上的平均光强分布和Strehl比，由此获得星光在大气湍流流场传输过程中能量衰减规律。

3.1 流场截面上的平均光强推导

根据推广惠更斯-菲涅耳原理，计算星光在L厚度截面湍流场传输过程中的平均光强。设进入湍流内该截面之前的光场为u0(ρ)，经过湍流中该截面传输后的光场uN(r)，经坐标变换，ρ1-ρ2=ρ，ρ1+ρ2=2R，推导平均光强[13]为：

(12)

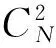
假设初始光场为聚焦的高斯光束：

(13)

O为光束截面上光强降为中心值的e-1时的光束半径。将式(13)代入式(12)后对R积分，并利用平方近似对积分结果再次积分得到平均光强为：

=

(14)

式中：ρ0=0.48r0。

3.2 流场截面上的星光Strehl比计算

Strehl比是研究湍流流场降晰效应的重要参数。用星光通过流场中L厚度截面时的Strehl比来衡量该流场截面造成的星光能量损失程度。由统计光学理论知Strehl比(式中用S表示)用光学传递函数可表示为[14]：

(15)

式中：I为星光通过流场传输的像平面最大光强，I0为初始像平面最大光强；τ(x,y)为光学传递函数。

由式(15)可得到Strehl比的一阶矩(即均方光强比)为:

(16)

式中：设τ的脉动完全相关。<τ(x,y)>为均方光学传递函数：

(17)

将式(17)代入式(16) 得：

=

(18)

根据波面误差方法[6]推得Strehl比为：

(19)

(20)

将式(20)代入式(19)即可得到该流场截面上的星光Strehl比。

4 数值仿真与结果分析

仿真条件：星敏感器光学系统口径=40mm；焦距=48.6mm；视场角=15°。电耦合器件(Charge coupled device,CCD)阵列取512×512，像元尺寸为25μm；星图取512×512的灰度图形。将流场数据在X-Y平面内由56mm×56mm插值为512×512与像素点阵匹配。设星光入射角为90°(即星光导航最优星光入射角度)，对星光穿过湍流流场的偏折及光强衰减情况进行仿真。

4.1 平流层大气湍流流场模拟

根据式(2)及其参数设定，基于Fluent仿真软件对海面上空水蒸气体积分数为0.2时和活火山上空气溶胶体积密度为2μm3/cm3时两种极度环境下的大气湍流进行数值模拟。

气体立方体模型边长为0.5m，对其底面加热对流条件。并取该模型底部56mm×56mm×160mm密度变化较为剧烈的湍流场区域进行研究。该区域的密度分布仿真结果如图2和图3所示。

对比图2(a)和图3(a)可以看出,活火山上空湍流现象比较明显，海平面上空次之，其原因是气溶胶含量较多的大气密度大且黏稠。从湍流流场的密度脉动计算结果(图2(b)和图3(b))可以看出，随着局部气体黏滞性和密度的增大，相对周边湍流密度脉动程度加剧，活火山上空大气湍流脉动值远高于海平面上空大气湍流脉动值。

4.2 海平面上空大气湍流对星光过程的影响

在图2(a)、(b)中选取密度值变化较大的8个截面，其分别取在距星光入射平面0.03m、0.05m、0.07m、0.09m、0.11m、0.12m、0.14m处和出射面。

4.2.1 星光偏折仿真

根据式(11)计算44颗导航星的星光通过上述8个截面后的偏折程度，并用星点质心偏移进行描述，见图4。其中第4颗、第6颗以及第7颗星点的质心偏移最大，分别为0.0005154m、0.0005166m和0.0005113m。其原因是这三颗星的星光经过了0.16m处的湍流强度较大的大气，使得光线偏折现象尤为严重。可以假设若星光穿过海平面上空40km厚的平流层，并且所经过区域均为湍流强度较大区域，其最大传输偏折可达到129.15m。

4.2.2 星光平均光强衰减仿真

在图4中选出1～12号星,设其光线分别通过海平面上空流场区域中的各截面, 根据式(14) 计算截面上的平均光强,得到流场区域中平均光强衰减曲线,如图5所示。

由图5可知，星光在0.03m和0.09m截面上的平均光强出现剧烈衰减。结合图2(b)密度脉动场可以看出，这两处的密度脉动值均有剧烈增加，分析认为：湍流密度变化较大(密度脉动大)时，通过该湍流区域的星光能量快速衰减。

4.2.3 星光偏折及Strehl比的综合评价仿真

设KGD=2.2×10-4,根据式(6)、(11)和(19)，对图4中的3号及6号星进行偏折和光强衰减的综合仿真，结果见图6。从图6可以看出，星光穿过流场中的各截面时产生的偏折及其Strehl比值。对照图2(a)、(b)可知，3号星光传输经过的流场区域密度脉动较大，Strehl比较小，即光强衰减较大。从原始的平均光强度1.17×1021Cd照度，衰减降晰至0.145×1021Cd照度，星等降低了2.2等。而图6中的6号星的传输流场区域密度脉动较小，Strehl比较3号星要大的多，说明光强衰减较小。

图7是将原始星点图及穿过湍流流场降息后的星点图整合，下方两小图中位置偏左且直径较大的星点为原始星点，位置偏右且直径较小的星点为降晰星点。由图7可知，3号星较6号星暗(见右上角图)，而6号星较3号星的星点偏移大(见下方两图)。

4.3 活火山上空大气湍流对星光过程的影响

在图3(a)、(b)中选取密度值变化较大的6个截面，其分别取在距星光入射平面0.02m、0.04m、0.10m、0.12m、0.14m处和出射面。

4.3.1 星光偏折仿真

与第4.2.1节同理。计算44颗导航星的星光通过活火山上空流场区域的偏折程度，如图8所示。

由图8可知，星光经过0.16m厚度的气溶胶浓度大的湍流区域时，星点最大质心偏移量可达到0.005452m。若星光穿过40km厚的平流层，假设所经区域均为气溶胶湍流区域，其最大的传输偏折可达1.36km。远远大于海平面上空水蒸气湍流对星光传输造成的偏折。

4.3.2 星光平均光强衰减仿真

在图8中选取12颗星，设其光线通过活火山上空流场区域中的各截面,获得星光穿过流场的平均光强衰减曲线,如图9所示。

由图9可知，星光通过活火山上空大气湍流流场时，其能量有较大程度的衰减。结合图3(b)密度脉动场分布可知，同样发现星光穿过湍流流场区域的密度脉动越大，其能量衰减越严重。最大衰减程度可由原始1.17×1021Cd照度衰减降晰至0.106×1021Cd照度。相当于星等降低2.7等。

4.3.3 星光偏折及Strehl比的综合评价仿真

同第4.2.3节原理，对图8中的3号及5号星进行偏折和光强衰减的综合仿真，如图10所示。

对比图3(a)和图3 (b)可知，3号星所穿过的湍流流场区域不但密度值大，而且密度脉动也大，故导致其星光偏折和能量损耗均较大，在图10和图11中均可以看到。

5 结 论

本文研究了在平流层大气湍流流场中星光传输机理的模拟仿真方法，主要结论如下：

1)研究平流层环境特性对星光传输的影响机理，对平流层内飞行器星光导航建立导航星库是必须的。

2)用湍流流场中密度变化明显的多个截面上的星光偏折和平均光强统计描述星光传输过程中受大气的影响规律是全面和可行的。

3)星光穿过湍流区域后，星点质心发生明显偏移(即星光偏折)，其偏移程度与湍流流场的密度值有关，经过高密度的湍流区域越多，累积的星点质心偏移越大。若星光穿过40km厚平流层时，最大偏折可达到1.36km。

4)星光穿过湍流流场区域后，其亮度明显衰减，即星光光强衰减。其衰减程度与湍流流场密度脉动值有关，密度脉动值越大，星光光强衰减越严重。最严重情况可使星等降低2.7等。

[1] 杨博. 航天器星敏感器自主定位方法及精度分析[J]. 宇航学报, 2002, 23(3): 81-84. [Yang Bo. The method of autonomous position determination using star sensor and analysis of precision for spacecraft[J]. Journal of Astronautics, 2002, 23(3): 81-84.]

[2] 徐光勇.大气湍流中的激光传输数值模拟及其影响分析[D]. 成都:电子科技大学, 2008. [Xu Guang-yong. The numerical simulation and impact analysis of laser propagation in the atmospheric turbulence[D]. Chengdu: University of Electronic Science and Technology of China, 2008.]

[3] 刘景源. SST二方程湍流模型在高超声速绕流中的可压缩修正[J]. 宇航学报, 2012, 33(12): 1719-1726. [Liu Jing-yuan. Compressibility correction for the SST two equation turbulence model in hypersonic flows[J]. Journal of Astronautics, 2012, 33(12): 1719-1726.]

[4] 杨云军, 马汉东, 周传江. 高超声速流动转捩的数值研究[J]. 宇航学报, 2006, 27(1): 85-88. [Yang Yun-jun, Ma Han-dong, Zhou Chuan-jiang, Numerical research on supersonic flow transition[J]. Journal of Astronautics, 2006, 27(1): 85-88.]

[5] 徐向博. 大气湍流对激光传输的影响研究[D]. 长春: 长春理工大学, 2011.[Xu Xiang-bo. Effect on laser propagation in the atmospheric turbulence[D]. Changchun: Changchun University of Science and Technology, 2011.]

[6] 续敏, 王建立, 王建军，等. CCD在卫星星等测量中的应用[J].半导体光电, 2008, 29(1): 447-450.[Xu Min, Wang Jian-li, Wang Jian-jun, et al. Application of CCD in satellite magnitude measurement[J]. Semiconductor Optoelectronics,2008, 29(1): 447-450.]

[7] 洪汉玉, 张天序, 余国亮. 基于Poisson模型的湍流退化图像多帧迭代复原算法[J]. 宇航学报，2004, 25(6): 649-654 . [Hong Han-yu, Zhang Tian-xu, Yu Guo-liang. Iterative multi-frame restoration algorithm of turbulence-degraded images based on Poisson model[J]. Journal of Astronautics, 2004, 25(6): 649-654.]

[8] Ruan W C, Cen Z F, Li X T,et al. Simulation and analysis of nonlinear self-focusing phenomenon based on ray-tracing[J]. Acta Physica Sinica, 2013,62(4):044202.

[9] Xue B D, Zheng S L, Cui L Y. Transport of intensity phase imaging from multiple intensities measured in unequally-spaced planes [J]. Optics Express, 2011, 19(21): 20244-20250.

[10] Paolucci S. Direct numerical simulation of two-dimensional turbulent natural convection in an enclosed cavity [J]. J. Fluid Mech., 1990, 215: 229-262.

[11] Jones W P, Launder B E. The prediction of Laminarization with a two-equation model of turbulence [J]. Journal of Heat and Mass Transfer, 1972, 15(2):301-314.

[12] 王润轩.一种变折射率光学系统光线追迹的新方法[J].激光技术,2004, 28(6):664-666.[Wang Run-xuan. A new method of ray tracing in gradient index optics[J]. Laser Technology, 2004, 28(6): 664-666.]

[13] 刘维慧.激光在大气湍流中传播时光强起伏的初步分析[D]. 成都：电子科技大学, 2004.[Liu Wei-hui, Preliminary analysis of the the laser intensity fluctuation during transmission in atmospheric turbulence[D].Chengdu:University of Electronic Science and Technology of China, 2004.]

[14] 李桂春.大气光学[M]. 北京：国防工业出版社，2006.

通信地址：北京航空航天大学宇航学院新主楼B1026房间(100191)

电话：(010)82317228

E-mail:yangbo@buaa.edu.cn

朱雪妍(1990-)，女，硕士，主要从事大气湍流对平流层星光导航中星光传输的影响研究。本文通信作者。

通信地址：北京航空航天大学宇航学院新主楼B1026房间(100191)

E-mail:zhuyy6677@sina.com

(编辑：牛苗苗)

Influence of Atmospheric Turbulence on Starlight Transmission During Satellite Celestial Navigation in Stratosphere

YANG Bo, ZHU Xue-yan

(School of Astronautics, Beihang University, Beijing 100191, China)

Based on the satellite celestial navigation, this paper studies the mechanism of the starlight transmission in atmospheric turbulence in the stratosphere, reveals the attenuation law of the starlight during transmission, and provides the theoretical basis for establishing the navigation star database and the compensation algorithm of a charge coupled device (CCD) star map. Segments with a certain thickness is proposed by intercepting the sections at the boundary of which the density and density fluctuation of the turbulent field has changed seriously. At the mean time the deflection and average intensity of the starlight after transferring through each section is calculated respectively according to the geometrical optic method and the statistical optic theory, and then the energy attenuation curve of the starlight during transmission through the whole stratosphere is derived either. Thek-εturbulencemodelisadoptedtosimulatethedensityanddensityfluctuationfieldoftheatmosphericturbulenceindifferentextremenaturalcases.Theresultsofthesimulationshowthatthestarlightwillbedeflectedobviouslyandthestarlightintensitywilldecayaftertravelingthroughthestratospherewithturbulence,whereitsdeflectionandattenuationarerelatedtothedensityandthedensityfluctuationoftheturbulence,respectively.

Satellite celestial navigation; Atmospheric turbulence; Atmospheric optical effects; Magnitude

2014-04-25;

2014-06-25

国家自然科学基金(61074183)；国家自然科学重点基金(91016004)

V

A

1000-1328(2017)04-0359-08

10.3873/j.issn.1000-1328.2017.04.005

杨 博(1960-)，女，博士，副教授，主要从事飞行器制导技术、航天器自主导航、深空探测自主导航制导及可重复运载器制导技术的研究。