虚拟惯量控制响应延时对控制效果的影响分析

齐 军，陈 磊，闵 勇，王小海，徐 飞，景志滨，宋新尧

（1.内蒙古电力（集团）有限责任公司，内蒙古自治区呼和浩特市 010010；2.清华大学电机工程与应用电子技术系，北京 100084）

0 引言

为实现“碳达峰、碳中和”目标，我国正加速构建以新能源为主体的新型电力系统。新型电力系统中，大量传统同步机组被采用电力电子接口的新能源所替代。采用常规控制的风电、光伏等新能源无法像传统同步发电机组一样提供惯量、一次调频等频率支撑，会显著恶化功率扰动下系统的频率响应。针对该问题，一种非常直接的思路通过控制使得新能源也具有类似同步机组的惯量和一次调频响应。因此，虚拟惯量控制近年来得到学术界和工业界极大关注[1-17]，被认为是改善系统频率响应的一种有效措施。虚拟惯量控制有两种实现方案：一种是虚拟同步机方案[3]，对传统电力电子变换器的控制系统进行根本性的改变，模拟同步发电机的响应特性；另一种是基于频率变化率（Rate of Change of Frequency，ROCOF）的附加控制方案[12]，作为一个外部控制回路直接加到现有变换器的控制系统中。目前，第二种方案更适用于已有设备的改造，也是本文研究的重点。

虚拟惯量控制是模拟同步机的惯量响应。但是，同步机惯量响应是一个物理过程，转速/频率变化和功率变化之间是没有延时的，而虚拟惯量控制是通过控制实现的，包含频率测量、指令生成、控制实现等过程，频率变化到输出功率变化之间存在无法避免的响应延时[18]。响应延时对控制效果会产生什么影响成为虚拟惯量控制研究和应用中的一个关键问题。从模拟同步机的角度出发，希望虚拟惯量控制的响应延时越小越好，延时越小，越接近同步机惯量响应。此外，惯量响应的一个主要特性是在功率扰动后短时间内输出较大的功率支撑，以降低频率变化率，进而降低最大频差。因此，传统观点一般认为虚拟惯量控制的延时越小越好，并在相关标准中提出了对响应延时上限的要求[14]。但是，虚拟惯量控制的响应延时对其控制效果具体有何影响，目前还未见全面深入的研究。

电力系统功率扰动下的频率动态指标主要包括：频率变化率、最大频差、稳态频差[19]。传统电力系统中，系统同步惯量不足导致频率变化率和最大频差变大，因此，虚拟惯量控制的控制效果包括改善频率变化率和最大频差。本文研究虚拟惯量控制响应延时对频率变化率和最大频差的影响。研究对象是包含同步机组的系统，频率仍然由同步机转速确定而且同步机参与一次调频，系统中包含电力电子接口电源（Power Electronic Interfaced Generation，PEIG）。这种系统结构在未来相当长时间内仍将是主流。研究发现，虚拟惯量控制的响应延时越小，对于减小频率变化率越有利，但是，对于最大频差则并非如此，一定的响应延时反而对减小最大频差有利，而且还可以降低对PEIG 调频功率和能量的需求，调频成本更低。这是和传统观点不一样的结论。

1 系统模型和虚拟惯量控制

本文在经典的系统频率响应模型[19]基础上，加上带有频率支撑控制的电力电子接口电源，如图1所示。图1 中，ΔPD为系统功率扰动，Δf为系统频率偏差，TJ为系统同步惯量，ΔPM为同步机调频机械功率，GSG(s)=为同步机调频环节的传递函数，ΔPL为负荷功率变化量，KL为负荷的频率调节效应系数，ΔPPE为PEIG 调频功率，GPE(s)=为PEIG 频率支撑的控制策略。为了简单起见，本文考虑电池储能系统，以避免PEIG 内部复杂动态特性的干扰。详细模型可参考文献[20]，但本文采用频率动态研究中更常用的简化模型[15，21]，将其视为一个受控功率源。

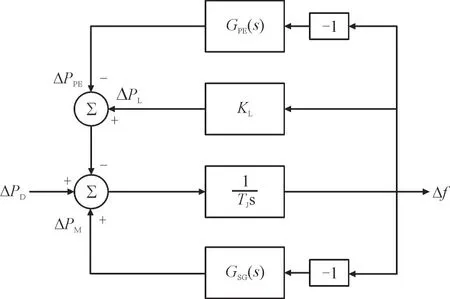
图1 系统频率响应分析模型Fig.1 Model for system frequency response analysis

同步机调频环节首先考虑最简单的一阶惯性环节，即GSG(s)=，KG为比例系数，TG为响应延时。PEIG 采用虚拟惯量控制，理想情况下的传递函数为：

式中：KD为惯量系数。

虚拟惯量控制的具体实现为PEIG 测量机端频率，进行微分后再乘以系数KD，得到调频功率指令并附加到PEIG 的功率控制环有功指令处，经过控制实现后改变设备输出功率，具体可参加文献[11-12]。本节先忽略频率测量、PEIG 功率控制的延时，此时的虚拟惯量控制是理想的。

设置图1 中的参数TJ=4.0 s，KL=1.5，GSG中KG=2.5，TG=10.0 s，GPE中KD=3.0。参数设置参考了一般系统的参数范围[19]，但需要说明的是，系统参数变化时，本文的研究结论不受影响，仍然成立。施加功率缺额扰动，ΔPD=-0.1。在PEIG 无频率控制和采用虚拟惯量控制两种不同情况下，系统频率曲线如图2 所示。由图2 可以看出虚拟惯量控制确实可以有效改善频率变化率和最大频差。

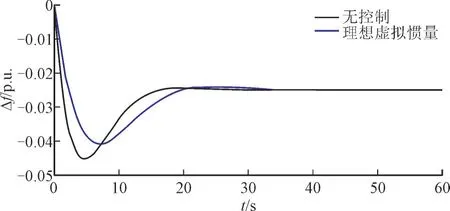
图2 系统频率曲线的比较Fig.2 Comparison of system frequency curve

PEIG 输出的调频功率如图3 所示，扰动瞬间频率变化率最大，调频功率最大，然后调频功率开始下降，稳态调频功率为零。因此，虚拟惯量控制主要是在扰动初期快速提供功率支撑，降低频率变化率，提升频率最低点。

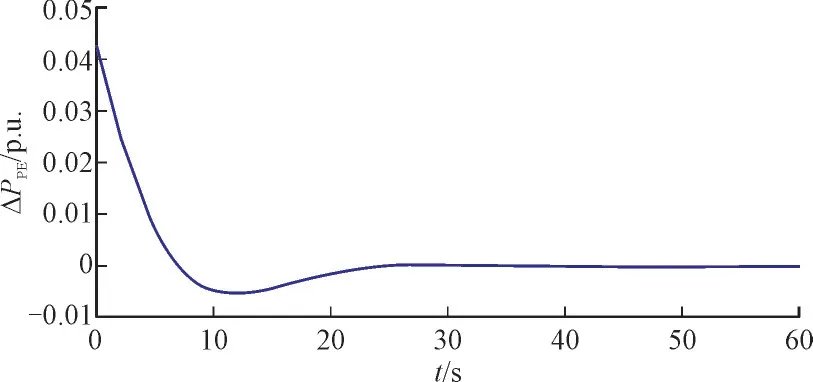
图3 PEIG采用理想虚拟惯量控制时输出的调频功率Fig.3 Frequency modulation power of PEIG with ideal virtual inertia control

2 虚拟惯量控制的响应延时

虚拟惯量控制以频率信号为输入，改变PEIG的输出电功率，包含频率测量、调频功率指令生成、调频功率指令控制实现等环节，即使调频功率指令生成环节采用式（1）的传递函数，频率测量和指令实现环节也是有响应延时的，一般简化的用一阶惯性环节表示，TD表示总的延时，此时，带延时的虚拟惯量控制传递函数为：

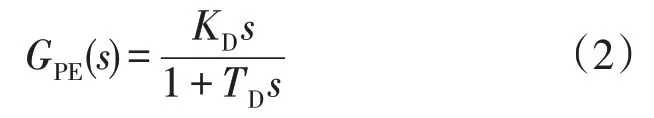
此外，还可能有一些人为添加的延时。实际中，理想微分环节难以实现，一般要增加惯性环节变为式（2）的形式；微分环节对噪声敏感，容易出现过操作，一般都加上一个低频滤波器对频率微分信号进行滤波，最简单的就是一个一阶惯性环节[5]，也会增大响应延时。此时，整个虚拟惯量控制环节的传递函数也可以用式（2）近似，TD反映整个控制环节的综合延时。

3 响应延时的影响

本节分析虚拟惯量控制响应延时对频率变化率、最大频差等不同指标的影响。

3.1 对频率变化率的影响

根据图1，功率扰动ΔPD为幅值为ΔPD0的阶跃信号时，频率偏差：

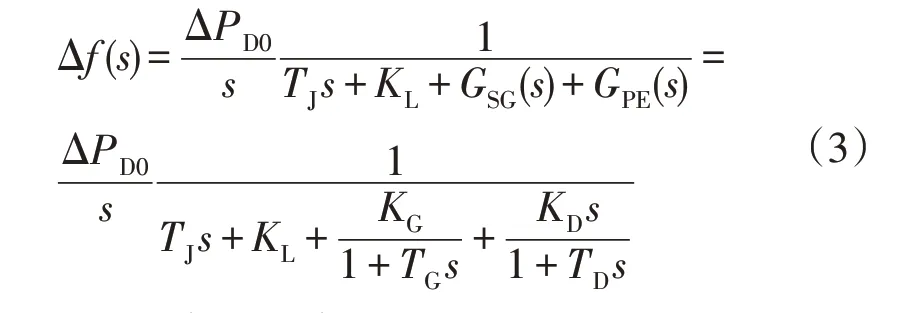
1）最大频率变化率

功率扰动后瞬间的频率变化率最大，其值等于：

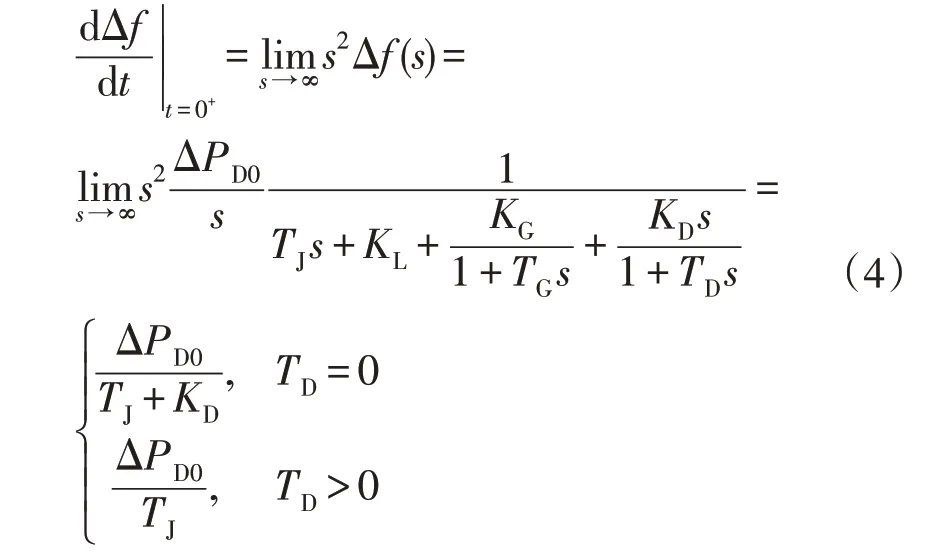
由于虚拟惯量控制的响应延时不可能达到0，即TD＞0，从式（4）可以看到虚拟惯量控制不影响扰动后瞬间的频率变化率，即实际的有延时的虚拟惯量控制无法减小最大频率变化率。

2）平均频率变化率

实际电网中，一般关注扰动后一段时间内的平均频率变化率[22]，典型的时段长度如200 ms 或500 ms。计算不同TD情况下扰动后200 ms 的平均频率变化率，其绝对值随TD的变化如图4 所示。由图4 可以看到，有延时的虚拟惯量控制可以减小扰动后一段时间的平均频率变化率，延时越小，效果越好，而且，当延时大到一定程度后，减小平均频率变化率的效果基本消失。因此，虽然实际的有时延的虚拟惯量控制无法减小最大频率变化率，但可以减小扰动后短时间内的平均频率变化率，而且，延时越小，减小平均频率变化率的效果越好。

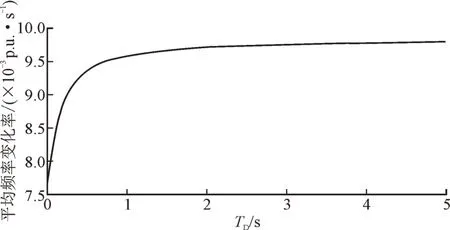
图4 200 ms平均频率变化率绝对值随延时的变化Fig.4 Variation of average ROCOF with response delay in 200 ms

3.2 对最大频差的影响

计算不同TD情况下系统的最大频差| Δf|max，结果如图5 所示。与对频率变化率的影响不同，零延时并不是最大频差最小的情况；随着延时的增加，最大频差减小，在某个延时下最大频差最小；然后随着延时的进一步增加，最大频差又开始增大。因此，延时对于虚拟惯量控制减小扰动后短时间内的平均频率变化率是不利的，但是对于减小最大频差则并非如此，一定的延时反而可以减小最大频差。这是之前虚拟惯量控制中没有注意到的现象。

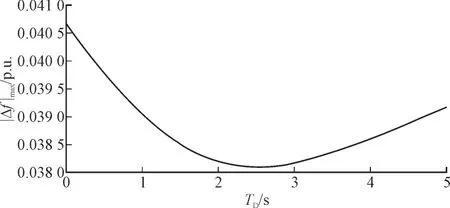
图5 最大频差随延时的变化Fig.5 Variation of maximum frequency deviation with response delay

为了更加清楚地显示一定延时对于改善最大频差的有利影响，画出理想虚拟惯量控制（TD=0 s）和TD=2.5 s 的有延时虚拟惯量控制情况下，系统的频率曲线，如图6 所示。

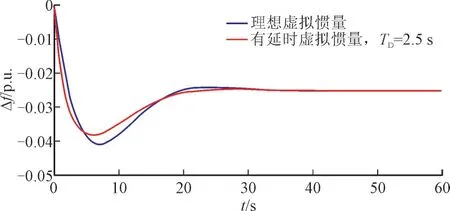
图6 理想虚拟惯量控制和有延时虚拟惯量控制系统频率曲线的比较Fig.6 Comparison of system frequency curves between ideal virtual inertia control and virtual inertia control with response delay

由图6 可以看到，有延时的情况下，初始阶段频率下降率确实更大，但最大偏差反而更小。因此，如果从减小最大频差的角度，虚拟惯量控制并非响应越快越好，一定的响应延时反而可以改善最大频差。

3.3 对控制成本的影响

频率下降情况下，PEIG 通过输出额外的功率ΔPPE提供频率支撑，而且额外功率需要PEIG 有调频能量储备。输出的功率越大、提供的调频能量越多，调频的成本越大。参考文献[22]中对调频控制成本的定义，主要考虑峰值功率和峰值能量2 个指标。峰值功率指标ΔPPE,max如式（5）：

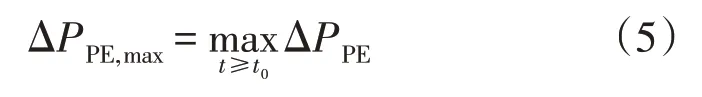
该指标直接决定PEIG 参与频率支撑时的调频功率容量。

峰值能量指标EPE,max如式（6）：

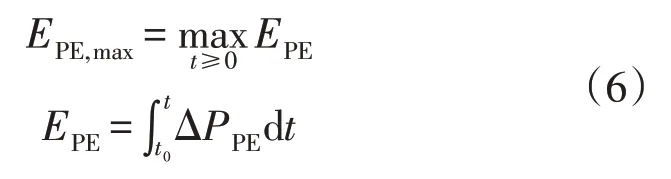
该指标直接决定PEIG 的调频能量容量。

计算不同TD情况下PEIG 调频的峰值功率和峰值容量，结果如图7 所示。由图7 可以看到，随着延时的增加，峰值功率和峰值容量单调下降。延时越大，PEIG 参与调频的控制成本越小。

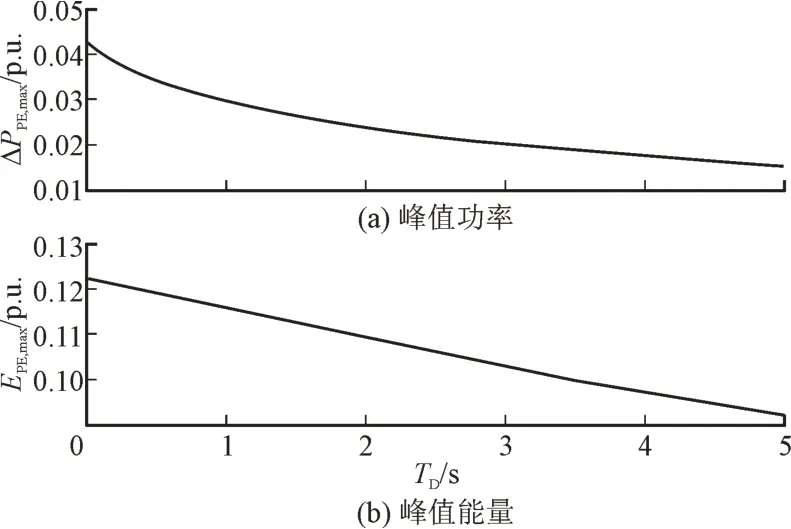
图7 峰值功率和峰值能量随延时的变化Fig.7 Variation of peak power and peak energy with response delay

图8 是理想虚拟惯量控制和TD=2.5 s 的有延时虚拟惯量控制的比较。

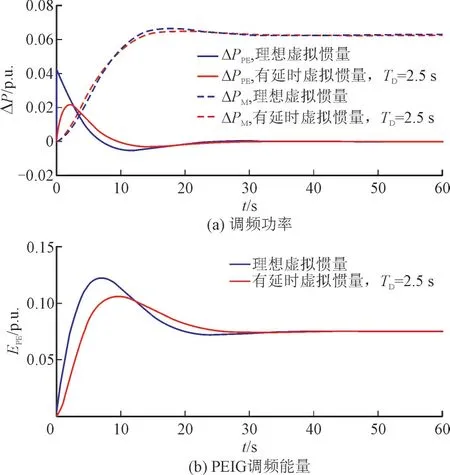
图8 理想虚拟惯量控制和有延时虚拟惯量控制系统的比较Fig.8 Comparison between ideal virtual inertia control and virtual inertia control with response delay

由图8 并结合图6 可以明显看到，与理想的虚拟惯量控制相比，在稳态调频功率、最终所输出的调频能量均一致的情况下，有延时虚拟惯量控制虽然初始阶段频率下降率更大，但减小最大频差的效果更好，而且所需的调频功率容量（即峰值功率ΔPPE,max）更小，最后的调频能量相同但调频能量容量（即峰值能量EPE,max）也更小。具体的比较如表1 所示。

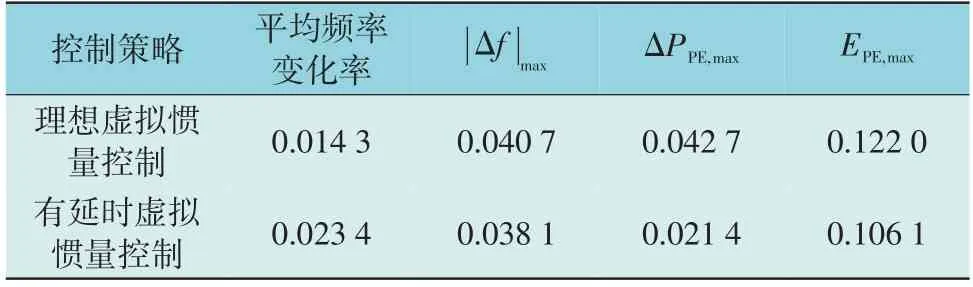
表1 虚拟惯量控制和一阶高通滤波控制具体指标比较Table 1 Indices comparison between virtual inertia control and first-order high-pass filter control

3.4 分析结果的讨论

本节关于响应延时影响的分析结果对于虚拟惯量控制的实施具有如下指导意义：虚拟惯量控制的延时是无法避免的，如果按照传统认识，需要努力去减小从测量到控制整个过程的延时，实际上是需要付出成本的。但是，根据本文结论，如果系统中频率变化率是主要约束条件，虚拟惯量控制是为了降低频率变化率，应该减小虚拟惯量控制的响应延时，以满足频率变化率的约束；如果系统中频率变化率满足要求，虚拟惯量控制是为了降低最大频差，则响应延时并非越小越好，就没有必要去减小延时，可以采用延时更大、成本更低的设备，甚至可以人为增加适当的延时减小最大频差，并降低对设备功率、能量容量的需求，能够以更小的控制成本实现更好的控制效果。

从图6 和图8（a）可看出，适当的延时反而有利于改善最大频差。有延时虚拟惯量控制策略下，初期频率下降更为迅速，让同步机更快的输出调频功率，频率下降率减小的更快，两者协调作用下，最低频率反而得到了改善。在仍然包含相当比例同步机的系统中，PEIG 和同步机的协调对于改善控制效果、降低控制成本十分关键，还需要进一步研究。

关于TD具体取值，本文通过仿真分析了平均频率变化率、最大频差、峰值功率、峰值能量等指标和TD之间的关系，其中平均频率变化率、峰值功率、峰值能量和TD之间的关系都是单调的，但最大频差随着TD增加先减小再增大，如何确定最优的TD还需要进一步研究。

4 多机系统仿真分析

下面在New England 10 机39 节点系统[23-24]中进行分析。在MATLAB 中利用m 语言建立系统机电暂态的动态方程，然后调用ODE 积分函数进行时域仿真。保留网络，不等值为图1 所示的单机系统。发电机采用四阶模型，带励磁和电力系统稳定器（Power System Stabilizer，PSS）；负荷采用恒功率加恒阻抗模型，考虑频率调节效应；调速器和原动机模型采用文献[24]中的模型。系统参数来源于文献[23-24]。该系统是电力系统分析中常用的测试系统，而且均采用详细模型，基于该系统的分析结果具有较高的可信性。

调速器采用PID 型调速器，传递函数Ggov(s)为：

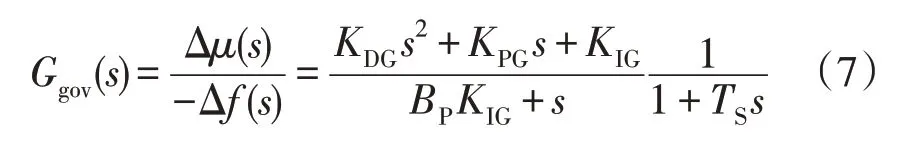
式中：Δμ为导叶/汽门开度变化量；μ为导叶/汽门开度；BP为调差系数；KPG，KIG，KDG分别为调速器的比例、积分和微分系数；TS为伺服系统的时间常数。

参数取值KPG=0.5，KIG=0.2，KDG=0.1，BP=0.4，TS=0.2 s。

系统中设定5 台水轮机和5 台汽轮机。水轮机模型Ght(s)如下：

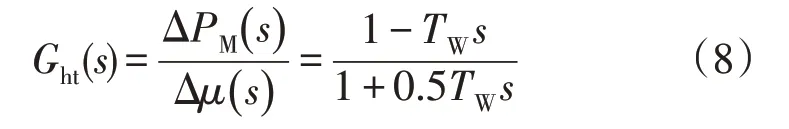
式中：TW为水启动时间，取值TW=2.0 s。

汽轮机模型采用计及高压蒸汽和中间再热蒸汽容积效应的二阶传递函数，如下：

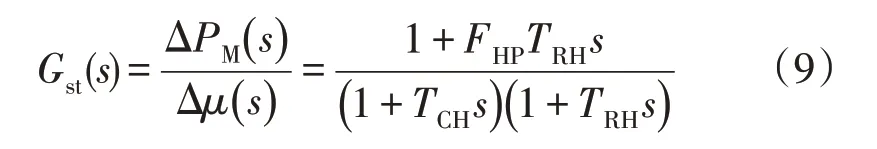
式中：FHP为高压缸稳态输出功率占汽轮机总输出功率比例；TCH为主进气容积效应时间常数；TRH为中间再热蒸汽容积效应时间常数。

参数取值FHP=0.4，TCH=0.3 s，TRH=4.0 s。

在节点5，14，17 分别加入电池储能，采用和文献[25]中类似的简化模型，直接用功率源表示，加入虚拟惯量控制，控制参数KD分别设为80，100，150，有延时虚拟惯量控制的TD设为3.0 s。理想虚拟惯量控制和有延时虚拟惯量控制的比较如图9 所示。图9 显示的结果与前面的分析相同：和理想虚拟惯量控制策略相比，有延时虚拟惯量控制虽然初始阶段频率变化率更大，但最大频差更小，所需的调频功率容量更小，调频能量容量更小。

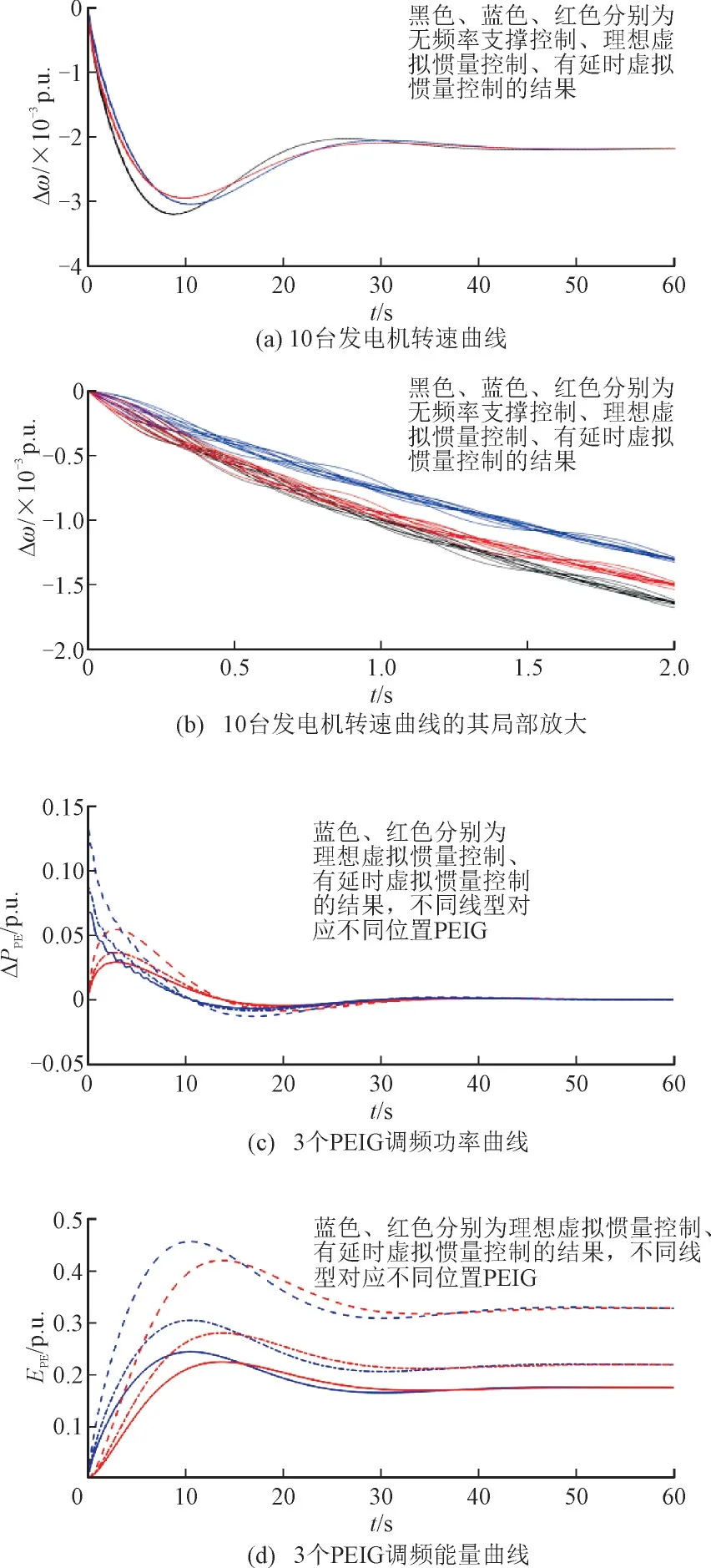
图9 详细多机模型中理想虚拟惯量控制和有延时虚拟惯量控制的比较Fig.9 Comparison between ideal virtual inertia control and virtual inertia control with response delay in detailed multi-machine system

5 结语

电力电子设备的虚拟惯量控制模拟同步机的惯量响应。同步机惯量响应是一个无延时的物理过程，而虚拟惯量控制通过控制实现，响应延时无法避免。从更好的模拟同步机惯量响应的角度出发，一般认为虚拟惯量控制的响应延时越小越好。本文对此问题进行了深入分析，发现了虚拟惯量控制响应延时对不同动态频率指标的影响。由于延时的存在，实际的虚拟惯量控制对功率扰动后的最大频率变化率没有作用，但可以减小扰动后短时间内的平均频率下降率，延时越小，减小平均频率变化率的效果越好。但是，延时对于最大频差的影响则不完全是负面的，随着延时的增大，最大频差反而下降，并在某个延时取值处获得最优值。此外，随着延时增大，调频功率峰值和能量峰值均降低，对设备调频的功率容量和能量容量需求降低，控制成本更小。

本文研究并不是提出了一种新方法，而是发现了和传统认识不一样的新现象，即虚拟惯量控制的延时并不是越小越好，而是根据控制目标不同而不同。系统频率响应模型和多机详细模型中的仿真均验证了本文结论的正确性。本文的研究结论对于虚拟惯量控制的实施具有指导意义。如果系统中频率变化率是主要约束，希望利用虚拟惯量控制降低频率变化率，则应该尽可能减小虚拟惯量控制的响应延时。在频率变化率满足要求的情况下，虚拟惯量控制主要用于降低最大频差，此时虚拟惯量控制并非越快越好，适当的响应延时反而可以减小最大频差，而且所需的调频功率容量和能量容量都更小，能够以更小的控制成本实现更好的控制效果。

关于虚拟惯量控制延时改善最大频差的机理以及延时的最优取值，本文目前只进行了一些简单的讨论，将是下一步研究的重点。