基于PCA-LMD-WOA-ELM的短期光伏功率预测

王鹏翔，沈 娟，王菁旸，林重驰

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.三峡大学土木与建筑学院，湖北宜昌 443002）

0 引言

目前，传统化石能源日益增长的需求对环境造成较大危害，绿色环保的可再生能源越来越受到重视。在双碳目标下太阳能作为国内外能源领域应用广泛、技术成熟的新能源之一，如何对其进行高效利用成为研究热点。太阳能利用中的光伏发电由于其简单、直接等优点成为主流应用形式，但其易受光照、温度等环境因素的影响，出力具有随机性和间歇性。光伏发电出力的随机波动性使得其大规模并入电网会对电力系统的稳定运行造成负面影响[1-2]。对光伏发电出力进行准确预测，可减弱其并入电网的波动性，有利于电网对新能源发电的调度，有利于电力系统的安全稳定运行。

国内外学者对于光伏预测的预测方法主要分为统计模型法和物理模型法。物理模型法是对光伏发电的实时云层图像以及太阳能转换为电能的物理过程进行精确的计算，通过精准的计算从而得出预测值[3]统计模型法是通过对光伏电站的历史出力数据以及天气历史数据进行分析、处理。再通过神经网络[4-6]，极限学习机[7-9]，支持向量机[10-12]等自适应学习算法对光伏发电功率进行预测。文献[13]提出了通过变分模态分解（Variational Mode Decomposition，VMD）算法降低数据的非平稳性，再结合稀疏高斯混合过程专家模型（Mixture of Sparse Gaussian Process experts model，MSGP）及深度回声状态网络（Deep Echo State Network，DESN）建立光伏发电短期预测模型，采用VMD 算法对数据的预处理提高了预测精度。文献[14-15]分别采用了不同的算法对BP 神经网络（Back Propagation Neural Network，BP）进行优化，与单纯的BP 神经网络相比，提高了收敛速度及预测精度。文献[16]提出构建基于天气分类和改进BP 神经网络的光伏发电功率预测模型，通过对天气类型的分类，在一定程度上提高了预测精度。

本文在现有的研究基础上，提出一种基于主成分分析（Principal Component Analysis，PCA）和局部均值分解（Local Mean Decomposition，LMD）鲸鱼优化算法优化后的极限学习机光伏功率短期预测模型。首先通过主成分分析法，筛选出与光伏发电功率相关性高的天气因素。再利用局部均值分解算法，将选取出来的天气因素及光伏发电功率序列进行分解，得到一系列具有不同特征的分量，然后将各分量通过鲸鱼优化算法优化的极限学习机进行预测，各分量所得到的的预测结果进行叠加，其和即为最终预测结果。将本文预测方法与传统的极限学习机（Extreme Learning Machine，ELM），鲸鱼优化算法（Whale Optimization Algorithm，WOA）优化后的ELM 模型进行对比分析，仿真结果证明，本文所提方法具有更高的预测精度。

1 基于WOA-ELM的光伏预测模型

1.1 ELM算法原理

ELM[17]相比于传统BP 神经网络、支持向量机等，算法结构更简单。通过对ELM 输入权重和隐含层数进行设置，随机产生权重和阈值初值，然后利用最小二乘法获得最优权重值及阈值。ELM 算法学习速度更快，且对非平稳信号的处理性能更强，其算法结构如图1 所示。

图1 ELM算法结构图Fig.1 ELM algorithm structure

图1 中，ELM 模型含输入层、隐含层和输出层：输入变量为N个，即N组不同的样本训练数据x j,j=1,…,N通过隐含层设置函数g(ai,bi,xj),i=1,2,…,T将样本数据映射至输出层矩阵Z。模型表达式如下[3]:

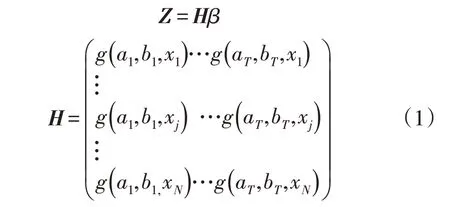
式中：H为极限学习机的隐含层输出矩阵；Z为极限学习机的输出矩阵；β为极限学习机隐含层与输出层之间权值的矩阵；ai为输入层所有节点与隐含层第i个节点间对应权值的矩阵；bi为第i个隐含层节点的阈值。

在隐含层输出矩阵H中，由最小二乘法计算出最优的权值为

式中：H+为矩阵H的广义逆矩阵。

1.2 WOA算法原理

鲸鱼算法通过模仿座头鲸搜索猎物行为而建立的一种优化算法，分为逐渐搜索和随机搜索[18-19]。逐渐搜索行为模型表达式为：

随机搜索行为模型表达式为：

式中:D为座头鲸到猎物处的距离；A和C为随机系数；X*(t)和X(t+1) 分别为当前最佳位置与下一迭代后最佳位置；t为当前迭代位置；Xrand为随机位置。

结合WOA 算法，可解决ELM 模型在样本训练中由于随机选取阈值和权值而导致输出结果相差较大的问题。通过WOA 算法寻找出阈值和权值，可增加ELM 模型用于预测时的精准度及平稳性。结合WOA 算法的ELM 模型流程图如图2 所示。

图2 鲸鱼优化算法的ELM原理图Fig.2 ELM schematic diagram of whale optimization algorithm

2 基于PCA-LMD-WOA-ELM 的光伏功率预测方法

2.1 PCA算法介绍

PCA 是一种降维的统计方法，它将众多具有一定相关性的数据，重新组合为一组表明各数据间相关性关系的指标[20-21]。而在光伏发电的原始数据中包括了光照辐射度，器件温度，天气温度，光伏发电功率多个影响因素。各影响因素间存在一定的相关性，通过PCA 对各影响因素进行筛选降维，降低相关性较低的因素对光伏功率预测精准度的影响。表1 为各类天气因素与光伏发电功率的相关系数。

表1 光伏功率与天气因素的相关系数Table 1 Correlation coefficient between photovoltaic power and weather factors

主成分分析法的计算原理如下：

有m个数据序列进行主成分分析：x1,x2,…,xm，有n个评价对象，第i个评价对象的第j个指标为xij。

首先对原始数据进行标准化，得到标准矩阵X∗，然后计算相关系数矩阵R，然后将特征值λ与特征向量e由特征方程|λI-R|=0 解得。根据式（7）计算各特征值贡献率，选取贡献率高的特征值所对应的特征向量组成矩阵。

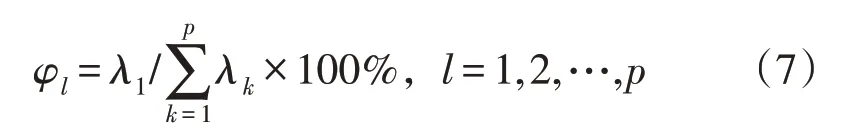
最后将原始数据矩阵换至m个特征向量的空间中。

式中:emp为原相关矩阵第m个特征值对应的p维特征向量；ym为第m个分量。

将光伏历史数据选取部分作为原始数据序列，由光照辐射度、器件温度、天气温度、气压、相对湿度和光伏功率共同组成，对部分数据进行主成分分析，得到表1 中相关系数及表2 的各成分贡献率。

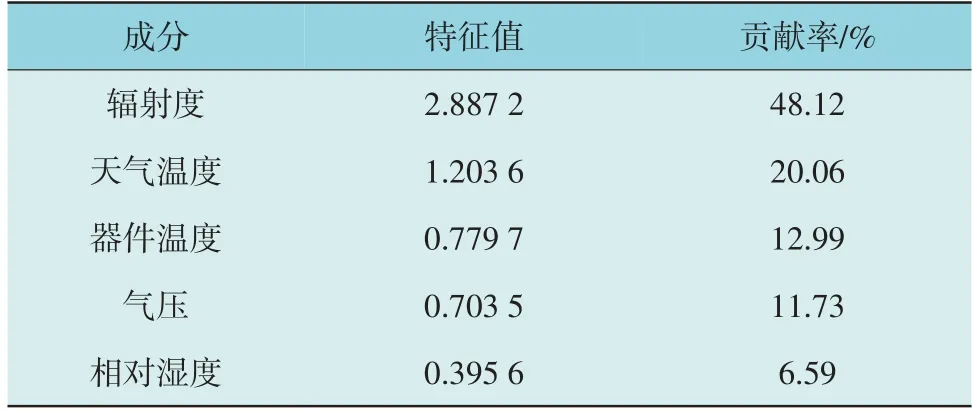
表2 主成分特征值及贡献率Table 2 Principal component eigenvalues and contribution rate

由表1、表2 可看出，光照辐射度与光伏功率的相关性最大，且成正相关性，天气温度和光伏功率的相关性也呈正相关，且相关性较高。器件温度与相对湿度和光伏功率的相关性较低，气压与光伏功率为负相关且相关性较低。因此，选取光照辐射度与天气温度作为预测模型的输入。

2.2 LMD算法原理

由于天气具有随机性、间歇性的特点，导致光伏发电功率也受到影响。而非平稳的信号会对光伏发电预测结果产生较大影响。LMD 可以将非平稳的信号分解为一系列具有不同特征的乘积函数（Product Function，PF）分量，在最大程度上避免由于天气的随机性和间歇性带来的影响[22-24]。分解步骤如下：（1）将原始信号x(t)中极值点ni全部找出来，计算极值点ni和ni+1的均值mi和包络值ai；（2）将所有的局部均值mi和包络值ai在对应时刻进行延伸，将延伸线用平滑线连接起来，由此计算出局部均值函数m11(t)以及包络函数a11(t)；（3）原始信号x(t)中分离m11(t)，得到h11(t)，用a11(t)对h11(t)进行解调，计算得到s11(t)；（4）s11(t)求包络函数a12(t)，若a12(t)为1，则s11(t)是纯调频函数，迭代结束，否则将s11(t)视为原始信号，重复上述步骤继续迭代，直到s1n(t)为纯调频函数止；（5）将上述步骤中得到的所有包络值相乘得到包络信号a1(t)，将a1(t)与s1n(t)相乘即得原始信号的第一个PF 分量，即：

将第一个分量PF 从原始信号中分离出来：

将剩余信号u1(t)视作原始信号，重复步骤（1）—（5），直到uk(t)是单调函数为止，迭代次数为k次。此时，x(t)可由k个PFi函数和残余分量uk(t)重组得到：

由于天气随机性、间歇性的特点，光伏功率具有同样的特点。根据主成分分析法，完成了对天气因素的筛选，将光照辐射度与光伏功率作为预测模型的输入，再通过局部均值分解算法对这两类数据序列进行分解，分解为具有不同特征的乘积分量，由于得到的残余分量过小且对预测并无影响，在仿真中不作考虑。通过WOA-ELM 预测模型对各乘积分量分别进行预测。光照辐射度与光伏功率的分解图如下图3 所示。

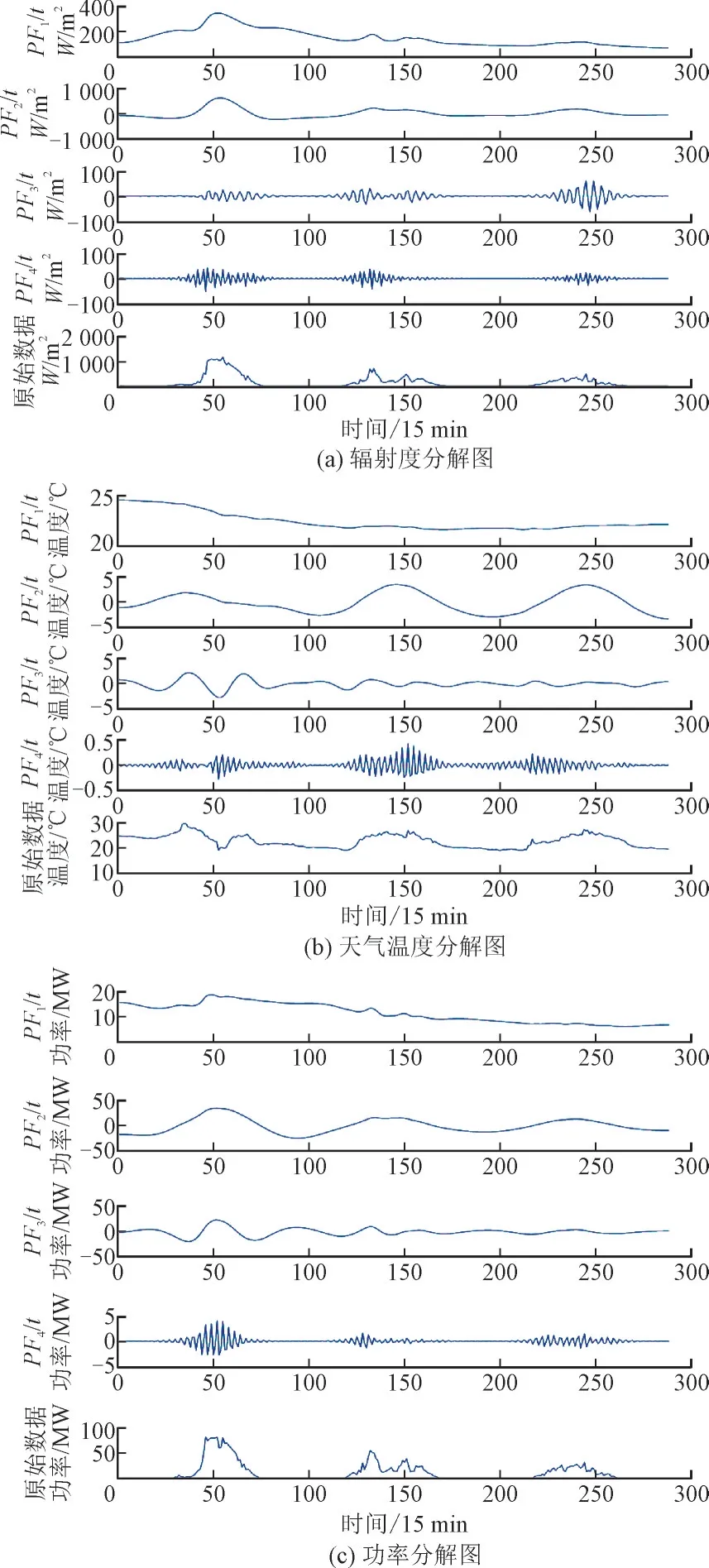
图3 LMD分解图Fig.3 LMD decomposition

2.3 基于PCA-LMD-WOA-ELM 的光伏功率预测模型

由本文上述所介绍的PCA 算法、LMD 算法、WOA-ELM 算法，提出一种新的光伏发电短期预测方法，预测方法步骤图如图4 所示，预测方法的具体流程如下:

图4 预测方法步骤图Fig.4 Step diagram of prediction method

1）由主成分分析法对各类天气因素进行选取，筛选出于发电功率相关系数高的因素作为模型输入变量。

2）将（1）中选取的数据序列进行局部均值分解，将原始数据序列分解为具有不同特征的分量，消除原数据序列波动性与随机性带来的不良影响。

3）将分解后的各子分量分别带入WOA-ELM预测模型中，得到各分量的预测结果，由于分解所得结果其和为原始数据，因此将各分量预测结果进行等权叠加即为最终预测结果。

4）根据误差指标对仿真结果进行分析，并与其他预测方法进行比较。

3 算例仿真分析

本文采用某光伏电站所采集的全年光伏发电功率数据以及对应时间段的天气数据，此光伏电站的最大装机容量为100 MW，所采集的数据间隔为15 min。通过Matlab 仿真软件建立本文所提预测模型，预测模型的输出结果与输入数据序列的时间间隔相同。在原始数据样本中选择七月的全部数据作为测试集，然后在全年中选出晴天、雨天、变化天气作为验证集。将预测当天的历史天气数据及历史光伏功率数据作为输入，通过PCA-LMD-WOAELM（方法1）获得晴天，雨天和阴天在未来1 d 内的变化曲线，同时引用传统的ELM（方法2），WOAELM（方法3）在同样条件下对3 种天气进行预测。

为对本文预测结果进行分析与评估，选取均方根误差（Root Mean Square Error，RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）对预测结果进行评估，其量值分别为ERMS和EMAP，同时与其他预测方法进行对比分析。通过误差指标值对各模型的预测结果进行比较分析。下图5—7 分别为晴天、雨天、变化天气在1 d 内各预测模型结果，表3 为各预测模型误差指标值。

表3 不同天气下各模型误差指标Table 3 Error indicators of each model under different weather conditions

图5 晴天时各模型预测结果Fig.5 Prediction results of each model in sunny days

式中：n为预测样本的总数；pi为预测功率值；qi为实际功率值；xˉ为实际功率平均值。

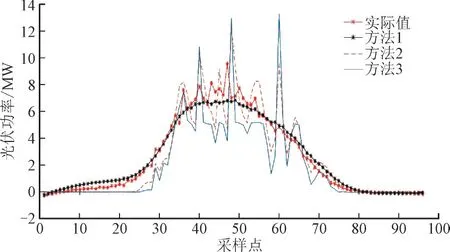
图6 雨天时各模型预测结果Fig.6 prediction results of each model in rainy days

由图5—图7 及表3 可知，通过鲸鱼优化算法优化过得极限学习机的预测效果，明显更优于传统的极限学习机模型，而将数据进行降维和特征提取的PCA-LMD-WOA-ELM 模型的预测效果更优于单纯的WOA-ELM 模型。在晴天时，ELM 模型的RMSE 和MAPE 分别为7.340 1 和14.684 5，预测效果最差，WOA-ELM 模型的RMSE 和MAPE 相较于传统ELM 分别下降至5.746 5 和10.357 4，预测效果较好，PCA-LMD-WOA-ELM 的误差指标值最小，可以看出数据处理对于预测模型的重要性。在下雨天，3 种模型的RMSE 分别为1.822 8，1.438 4，0.527 9，MAPE 分别为37.615 7，30.361 2，10.357 4，同样可以看出3 种模型在预测效果上的优劣。在变化天气的条件下，传统ELM 和WOA-ELM 的误差指标相差较小，但是仍然有一定差距，且仍是本文所提模型预测效果最优。

图7 突变天气时各模型预测结果Fig.7 Prediction results of various models in abrupt weather

通过对于3 种模型误差指标的详细分析，结合仿真图的对比可得，本文所提预测模型在数据分析、处理上明显优于其他模型，预测结果的稳定性较高，平稳性更好。

4 结论

本文针对目前光伏预测中存在模型输入影响因素较多，光伏受天气扰动大的问题，提出一种基于PCA-LMD-WOA-ELM 的组合式光伏预测方法。基于某光伏电站的历史数据，结合本文所提预测模型，通过仿真实验分析，得出如下结论:

1）针对影响因素较多的问题，通过PCA 可以很好的对数据进行筛选降维，将相对湿度、气压等相关性不大的数据筛选后，由仿真图与数据对比可看出，预测结果有明显的提升。

2）针对光伏功率易受到天气因素的影响，使得光伏功率同样具有随机性与间歇性的特点，提出使用LMD 算法将数据序列进行分解为多个分量，各分量具有不同的特征，再由各分量分别预测，最后预测结果叠加，由仿真图及数据可看出，预测效果更优。

3）本文将两种算法与WOA-ELM 结合，对目前光伏预测存在的问题进行了改进，且本文所提方法对于多种天气都能较准确的预测。