基于阻抗分析法的风储并网系统谐波稳定性分析
苏大威,徐伟,张琦兵,陈颖杰
(1.国网江苏省电力有限公司,江苏南京 210024;2.南瑞集团有限公司(国网电力科学研究院有限公司),江苏南京 211106)
0 引言
随着煤、石油等化石资源的大幅度减少,风、光等可再生能源的发电及并网问题已成为研究热点[1-4]。几乎所有的可再生能源都是通过并网逆变器接入电网[5,6],大量并网逆变器的接入使系统更易发生谐波振荡,引起电网电压和并网电流畸变[7]。
并网逆变器阻抗的准确获取是进行谐波稳定性分析的关键前提之一[8],文献[9]将工况变化转化为扰动函数,建立起并网逆变器的大信号阻抗模型。文献[10]基于阻抗测量方法对多逆变器系统稳定性进行了校验。为提高并网逆变器接入下的系统稳定性,文献[11]提出一种加入权重系数的电网电压比例前馈控制策略,该策略可以提高系统在弱电网下的相位裕度,改善并网电流的质量。文献[12]提出—种适用于单相并网逆变器的具有频率自适应能力的改进型比例谐振控制方案,在电网电压谐波失真时,通过谐波补偿器与PR 控制器并联的方式,降低入网电流谐波畸变率。
为了应对渗透率逐渐增大的风光等随机性电源的接入,系统通常采用储能系统对其出力波动进行平抑。文献[13]给出储能逆变器并网工作的稳定判据:电网阻抗与逆变器输出阻抗之比需符合奈奎斯特判据。文献[14]利用阻抗分析法研究新能源分布式发电系统并网电流的谐波振荡。文献[15]通过建立诺顿等效电路和戴维南等效电路,分别分析了电流型控制和电压型控制的储能结构下逆变器并网的阻抗特性,但是没有讨论控制环路PI 控制器的影响。
在风机并网系统中,文献[16]计及网侧线路阻抗与变压器的影响,建立双馈风力发电机转子侧阻抗模型,对变压器与风力发电机耦合系统交互稳定性开展研究。文献[17]探讨了海上风电机组网侧变流器控制对风电场内部谐波谐振的影响。文献[18]建立了多机模型,但是没有研究各类风电机组的控制参数等因素变化对整个系统次同步谐振的影响。目前的研究大多是基于风机并网系统,没有涉及风储系统接入下对系统振荡特性的影响。
本文针对储能逆变器并网易引发谐振问题,在上述的研究基础上,根据储能并网系统的等效电路,利用奈奎斯特判据分析了风储并网系统的稳定性,研究储能和风电机组不同参数对系统谐波稳定性的影响。针对储能逆变器并入弱电网后易出现谐波振荡的问题,研究谐波振荡抑制策略,改善系统稳定性。
1 储能系统逆变器并网阻抗模型
1.1 储能系统阻抗模型
本文采用的储能逆变器并网系统的拓扑结构如图1 所示。其中,Iref为电流参考信号,G 为电流控制环路调节器(G=KP+Ki,KP,Ki分别为储能逆变器电流环比例增益和积分增益),Udc为电池储能系统直流电压,L1为逆变器侧电感,I1为逆变器侧电感电流,L2为网侧电感,Zg为外部网络阻抗,U为逆变器交流测输出电压,C为滤波电容,R为阻尼电阻,Ic为电容电流,Upcc为公共连接点(Point of Common Coupling,PCC)电压,Uc为电容支路电压,Ug为电网电压;Ig为网侧输出电流。

图1 储能系统逆变器并网拓扑结构Fig.1 Grid-connected topology of energy storage system through inverter
图2 为储能系统的控制框图。其中,上、下方虚线框Zg,Zout分别表示电网侧输出阻抗和逆变器侧输出阻抗,s表示复数频率,KPWM表示桥路放大增益,为简化分析,KPWM取1。
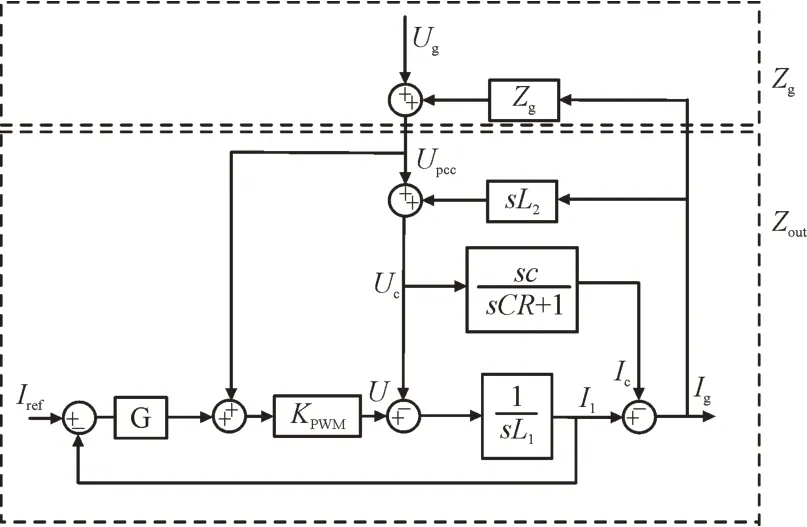
图2 储能逆变器并网系统控制框图Fig.2 Grid-connected control block diagram of energy storage inverter
根据图2,可得输出电流Ig的表达式如式(1)所示:
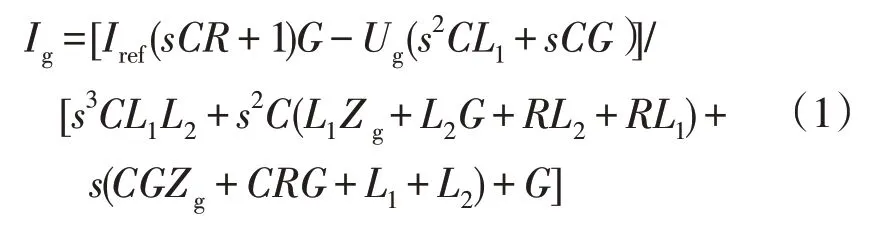
1.2 逆变器并网系统的等效电路模型
基于阻抗分析法,采用诺顿等效电路来表示逆变器并网系统的逆变器侧子系统,即由电流源Is与输出阻抗Zout组成的并联支路,如图3 所示。

图3 逆变器并网诺顿等效电路Fig.3 Norton equivalent circuit for inverter connected to grid
图3 中,电网侧子系统等效为电网等效阻抗Zg和理想电压源Ug串联。基于图3 所示的等效电路,可推导并网电流Ig表达式如式(2)所示:
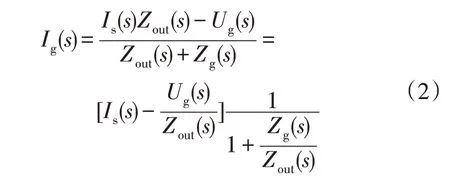
假设逆变器和电网均可独立稳定运行,此时电网电流Ig的稳定性由1/[1+Zg(s)/Zout(s)]决定,该表达式同样可看作一个前向通道为1、负反馈通道为Zg(s)/Zout(s) 系统的闭环传递函数。此时,若Zg(s)/Zout(s)满足奈奎斯特稳定判据,则逆变器在该电网条下能够稳定工作,且可根据Zg(s)/Zout(s)的奈奎斯特曲线来表示系统的稳定裕度。
由式(1)和式(2)可得诺顿等效电路的输出阻抗如式(3)所示:

1.3 基于入网电流反馈的有源阻尼控制
在电网阻抗较大,逆变器的并网稳定性受到较大的影响,易引发谐波,甚至发生并网电流发散造成系统不稳定[19]。为提高系统稳定性,采用基于入网电流反馈的有源阻尼控制,控制框图如图4 所示。通过采样入网电流Ig,经高通滤波器附加移相环节叠加到电流环输出。其中,k为反馈系数,ωh为滤波器的截止角频率;Igd为加入阻尼控制后的并网电流。

图4 基于入网电流反馈的有源阻尼控制Fig.4 Active damping control based on network current feedback
设定H(s)的前馈表达式如式(4):
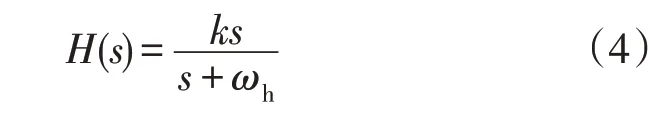
图4 的控制框图可推导出加入阻尼控制后的入网电流Igd表达式如式(5)所示:
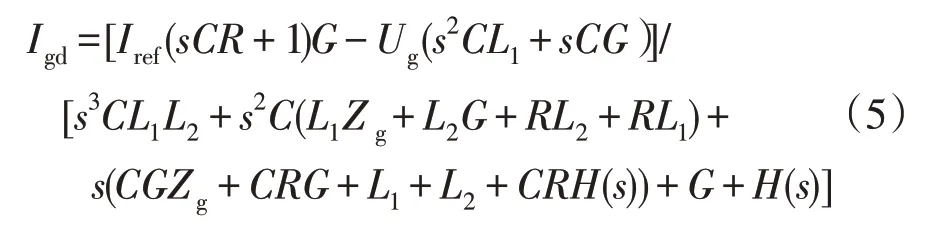
由式(2)和式(5)求得此时逆变器的等效输出阻抗如式(6)所示:

2 风储系统并网稳定性分析
2.1 风储系统并网模型
将储能系统并联在风电场的汇流母线处,分析风储并网系统的稳定性,风电场等值成单台风机。风机和储能系统经PCC 接入电网,其诺顿等效电路如图5 所示。其中,Zout1,Zout2分别为储能系统和风机的诺顿等效阻抗大小,Is1,Is2分别为储能系统和风机的诺顿等效电流源大小,Igt为风储系统总的并网电流。
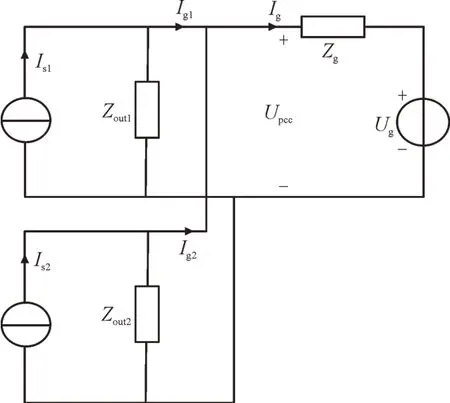
图5 风储系统并网诺顿等效电路Fig.5 Norden equivalent circuit for wind storage system
双馈风机阻抗模型采用文献[20]中考虑转子侧换流器的阻抗模型,风机的输入阻抗如式(7)所示:
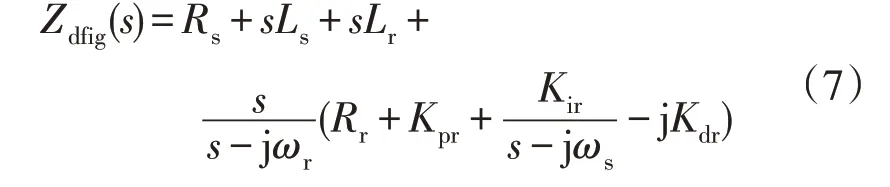
式中:ωs,ωr分别为定、转子角速度;Ls,Lr分别为定、转子漏感;Kpr,Kir分别为转子侧内环电流控制比例和积分增益;Kdr为转子电流环的交叉相增益。
由基尔霍夫定律,可得并网点电压Upcc表达式如式(8)所示:
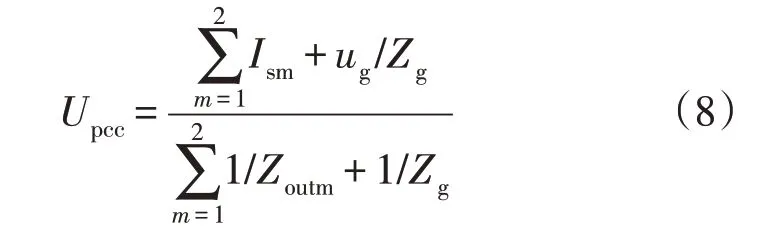
式中:Ism为第m个诺顿等效电流源大小;Zoutm为第m个诺顿等效阻抗大小。
基于图5 的等效电路,求得第m个诺顿等效电路的并网电流Igm为:
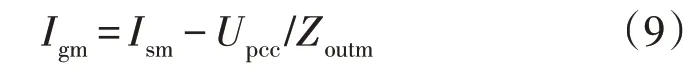
根据叠加定理可得总并网电流表达式为:

2.2 并网稳定性分析
采用级联系统稳定性分析方法,基于奈奎斯特判据,分析风储系统的并网稳定性。
2.2.1 风机转子侧内环电流环控制比例增益的影响
在风机转子侧内环电流控制比例增益Kpr参数设计方面,基于文献[21]取Kpr为0.26,0.32 和0.4,文献[22]取Kpr为0.3 和1.42,本文取Kpr为0.3,1 和3。取Kp=10,Ki=1,Kir=8,Kpr在不同值下Zg(s)/Zeq(s)的奈奎斯特曲线如图6 所示。由图6 可知,当Kpr分别为0.3,1 和3 时,奈奎斯特图均不会环绕(-1,0),表明系统稳定。Kpr分别为0.3,1 和3时,对应的相位裕度分别为49°,34°和29°,说明当风机转子侧内环电流环控制比例增益Kpr从0.3 增大至3 时,系统稳定性降低。
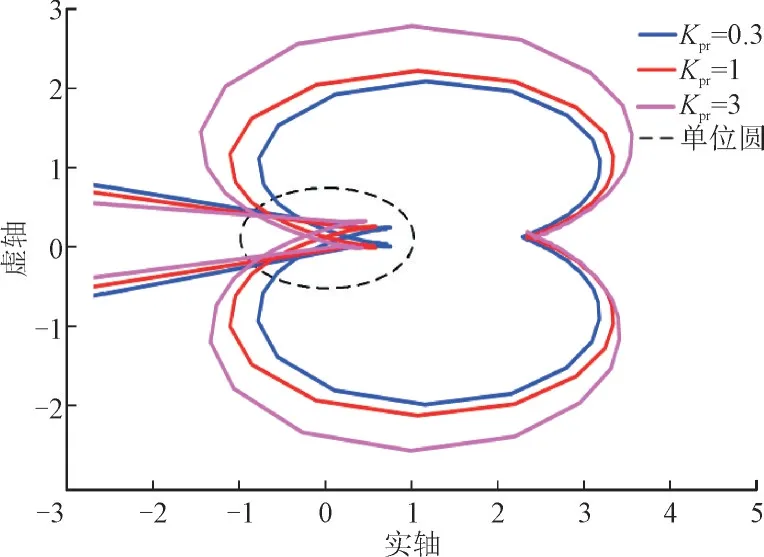
图6 不同Kpr下的奈奎斯特图Fig.6 Nyquist diagrams under different Kpr
2.2.2 风机转子侧内环电流环控制积分增益的影响
在风机转子侧内环电流控制积分增益Kir参数设计方面,基于文献[23]取Kir为8 和30,本文取Kir为8,20 和40。取Kp=10,Ki=1,Kpr=0.3,Kir在不同值下Zg(s)/Zeq(s)的奈奎斯特曲线如图7 所示。由图7 可知,当Kir分别为8,20 和40 时,奈奎斯特图均不会环绕(-1,0),表明系统稳定。Kir分别为8,20 和40 时,奈奎斯特变化较小,对应的相位裕度分别为49°,47°和46°,说明当风机转子侧内环电流环控制积分增益Kir从8 增大至40 时,对系统稳定性影响较小。
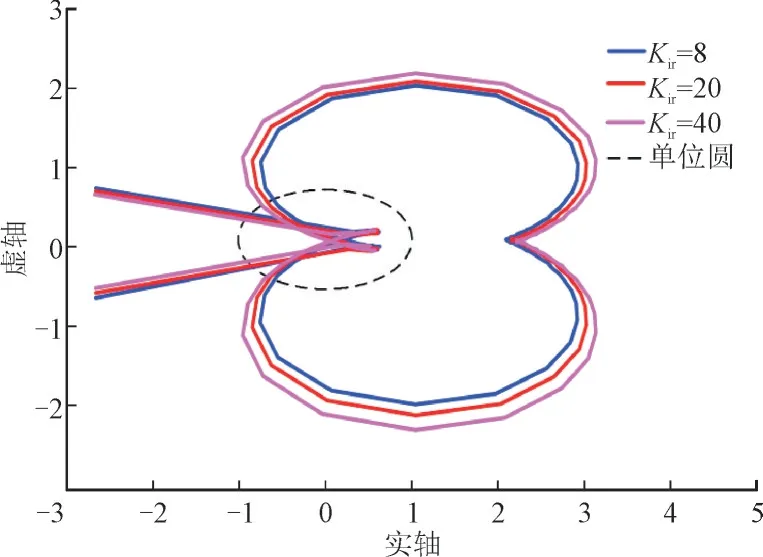
图7 不同Kir下的奈奎斯特图Fig.7 Nyquist diagrams under different Kir
2.2.3 储能逆变器电流环比例增益的影响
在储能逆变器电流环比例增益Kp参数设计方面,基于文献[15]取Kp=10,文献[24]取Kp=0.01,本文取Kp为1,5 和10。在风储并网系统中,风机参数取较优值(Kpr=0.3),固定Ki=1 时,研究不同Kp对系统稳定性的影响,相应的Zg(s)/Zout(s)奈奎斯特图如图8 所示。由图8 可知,当保持Ki=1 不变,Kp分别为1,5 和10 时,奈奎斯特图均不会环绕(-1,0),系统稳定。Kp分别为1,5 和10 时,系统相位裕度分别为37°,44°和49°,说明系统相位裕度会随着电流环比例增益Kp的增大而增大,即Kp的增大有利于系统稳定性的提高。
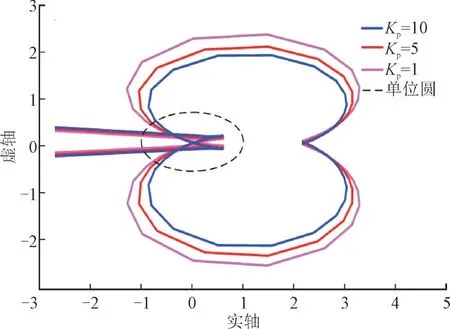
图8 不同Kp下的奈奎斯特图Fig.8 Nyquist diagrams under different Kp
2.2.4 储能逆变器电流环积分增益的影响
在储能逆变器电流环比例增益Ki参数设计方面,基于文献[15]取Ki=10,文献[25]取Ki=0.01,本文取Ki为1,5 和10。在风储并网系统中,风机参数取较优值(Kpr=0.3),固定Kp=10 时,研究不同Ki对系统稳定性的影响。Ki取不同值时,Zg(s)/Zout(s)的奈奎斯特曲线如图9 所示。由图9 可知,当Ki分别为1,5 和10 时,奈奎斯特图均不会环绕(-1,0),表明系统稳定。Ki分别为1,5 和10 时,奈奎斯特图无明显变化,对应的相位裕度均为49°,说明当储能逆变器电流环积分增益Ki从1 增大至10 时,对系统稳定性影响不大。
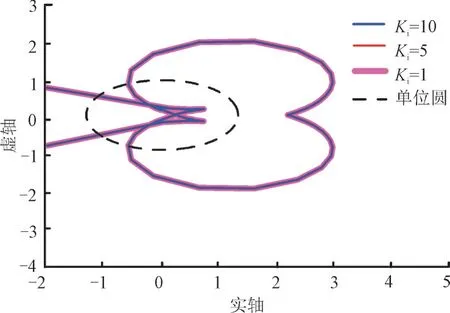
图9 不同Ki下的奈奎斯特图Fig.9 Nyquist diagrams under different Ki
2.3 加入阻尼控制后风储系统并网稳定性分析
为提高风储系统并网的稳定性,在储能系统侧采用1.3 节所提的基于入网电流反馈的有源阻尼控制方法。当风机参数设置的较差时(Kpr=3),系统相位裕度较小,研究此时阻尼控制对改善系统稳定性的效果。反馈系数k分别取1,5 和10 时的奈奎斯特图如图10 所示。由图10 可知,加入基于入网电流反馈的阻尼控制后,系统相位裕度增大,稳定性得到改善;反馈系数分别为1,5 和10 时的相位裕度分别为45°,51°和54°,说明系统相位裕度会随着反馈系数的增大而增大,即反馈系数k的增大有利于系统稳定性的提高。
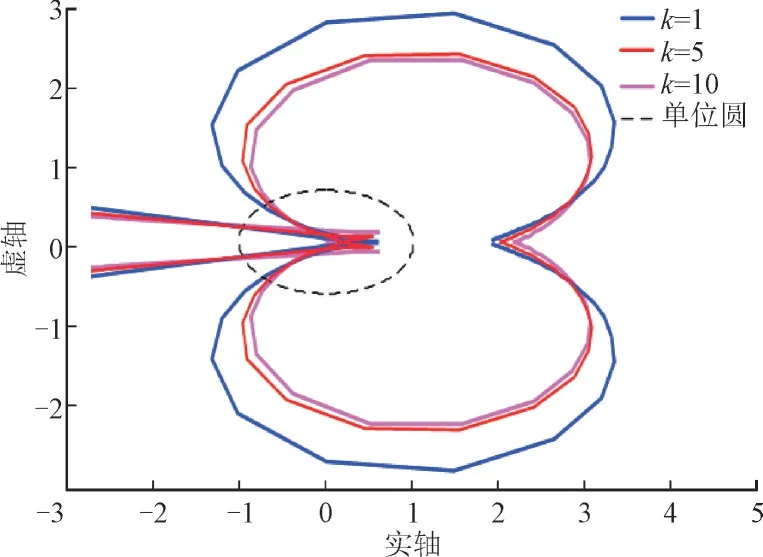
图10 不同k下的奈奎斯特图Fig.10 Nyquist diagrams under different k
图11 给出了当Kp=10,Ki=1,k=10,ωh变化时的奈奎斯特曲线。由图11 可知,ωh分别为1 000 rad/s,2 000 rad/s 和5 000 rad/s 时的相位裕度分别为54°,52°和51°,说明系统相位裕度会由于ωh增大而减小,即ωh的增大不利于系统稳定性的提高。
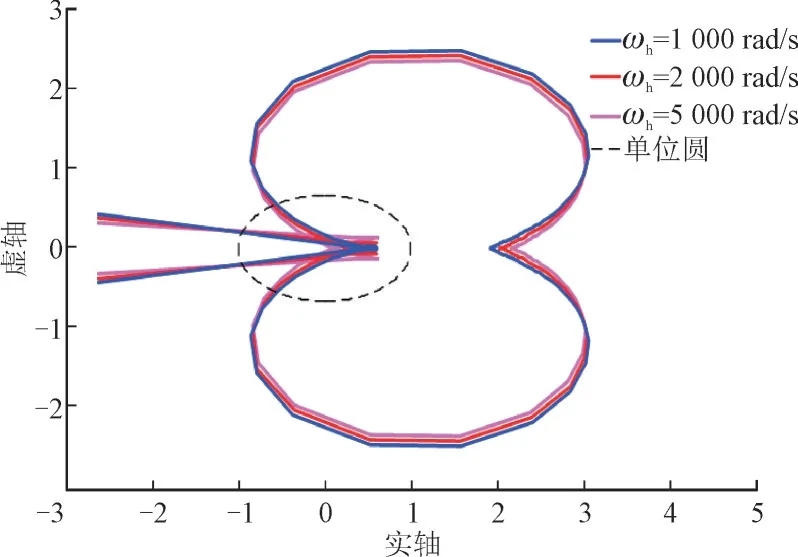
图11 不同ωh 下的奈奎斯特图Fig.11 Nyquist diagrams under different ωh
加入阻尼控制且参数设置较好时(k=10,ωh=1 000 rad/s),阻尼控制加入前后系统的幅频特性如图12 所示,由图12 可知,无阻尼控制时系统的相角裕度为20°,加入阻尼控制后,风储系统等效输出阻抗和电网阻抗交截点向更高频率段移动,对应的相角裕度增大至59°,所提的有源阻尼控制方法提高了系统的稳定性。
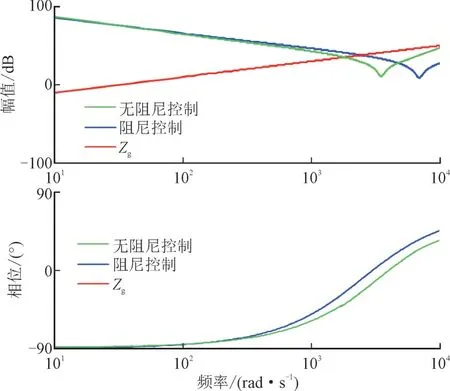
图12 有无阻尼控制下阻抗特性伯德图Fig.12 Bode diagram of impedance characteristics with or without damping control
3 仿真验证
为了对2.2 节分析结果进行仿真验证,在Matlab/Simulink 中搭建风储并网系统模型,风机由5 台1.5 MW 的双馈风机等值成单台容量为7.5 MW的风电机组参,储能容量设置为风电机组的20%。
3.1 风机转子侧内环电流环控制比例增益的影响
图13 给出了Kpr取不同值时风储系统并网电流Ig的波形。由图13 可知,并网电流的总谐波失真(Total Harmonic Distortion,THD)在Kpr取为0.3,1和3 时分别为3.88%,8.27%和12.14%,并网电流波形在Kpr从0.3 增大至3 时畸变率升高。说明在Kpr取值增大时,并网电流谐波稳定性降低,与2.2.1 节阻抗分析法得到的结论一致。
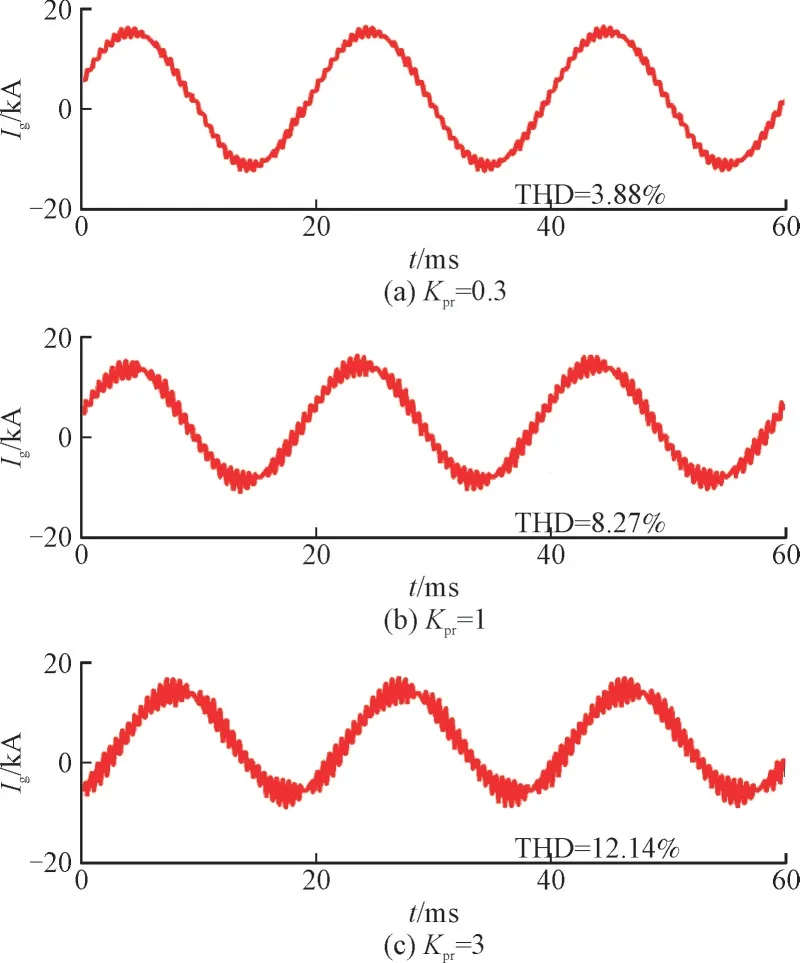
图13 不同Kpr下电流仿真波形Fig.13 Current simulation waveforms under different Kpr
3.2 风机转子侧内环电流环控制积分增益的影响
图14 给出了Kir取不同值时风储系统并网电流Ig的波形。由图14 可知,并网电流的THD 在Kir取为8,20 和40 时分别为3.88%、4.13%和4.25%,并网电流波形在Kir从8 增大至40 时变化不大。说明在Kir取值变化时,对并网电流影响很小,与2.2.2节阻抗分析法得到的结论一致。
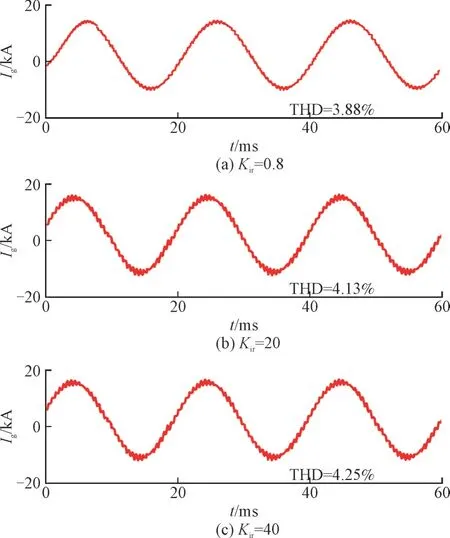
图14 不同Kir下电流仿真波形Fig.14 Current simulation waveforms under different Kir
3.3 储能逆变器电流环比例增益的影响
设置Ki=1,图15 给出了Kp取不同值时风储系统并网电流Ig的波形。由图15 可知,并网电流THD 在Kp取为1,5 和10 时分别为7.58%,4.61%和3.88%,并网电流在Kp=1 时畸变最大,在Kp=10时畸变最小。说明在Kp取值变大时,并网电流谐波稳定性更好,与2.2.3 节阻抗分析法得到的结论一致。
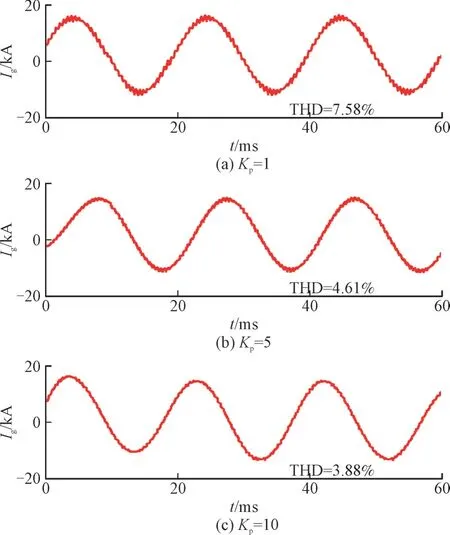
图15 不同Kp下电流仿真波形Fig.15 Current simulation waveforms under different Kp
3.4 储能逆变器电流环积分增益的影响
设置Kp=10,图16 给出了Ki取不同值时风储系统并网电流Ig的波形。
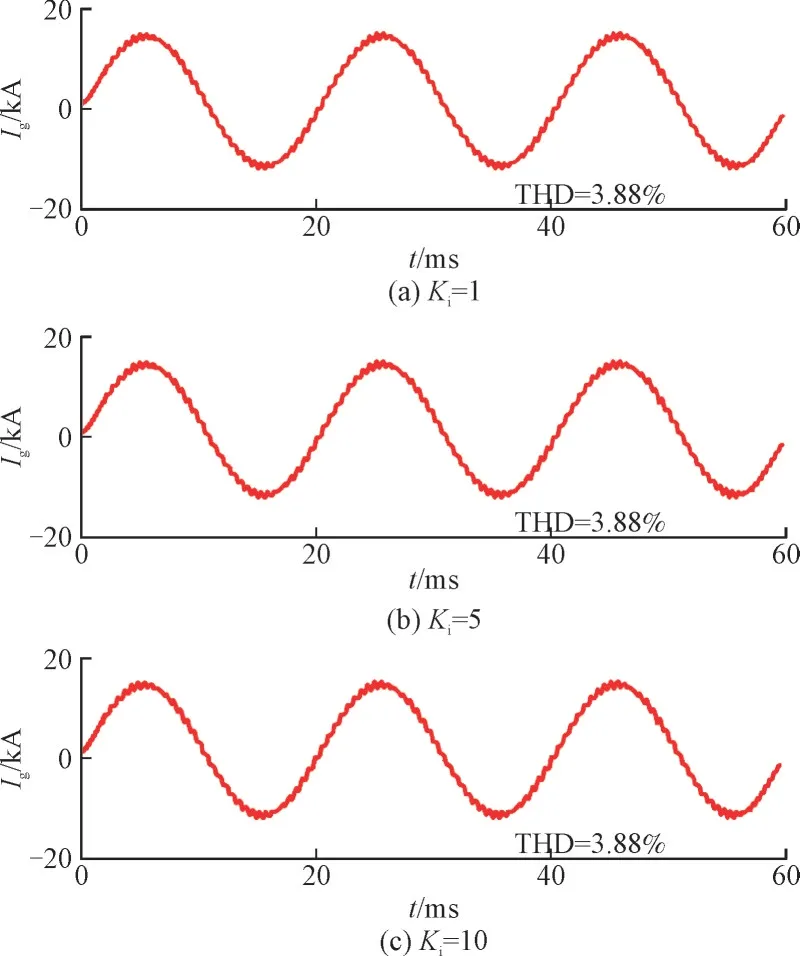
图16 不同Ki下电流仿真波形Fig.16 Current simulation waveforms under different Ki
由图16 可知,并网电流的THD 在Ki取为1,5和10 时均为3.88%,并网电流波形在Ki从1 增大至10 时无明显变化。说明在Ki取值变化时,对并网电流影响很小,与2.2.4 节阻抗分析法得到的结论一致。
3.5 基于入网电流反馈的有源阻尼控制的影响
分别采用无阻尼控制、有阻尼控制且控制参数设置较差(k=1,ωh=5 000 rad/s)、有阻尼控制且控制参数设置较好(k=10,ωh=1 000 rad/s)3 种情况进行仿真对比,3 种情况下的入网电流仿真波形如图17 所示。由图17 可知,当有阻尼控制且控制参数设置较差时,电流波形的THD 由无阻尼控制的12.14%下降到10.56%,抑制效果不明显;当有阻尼控制且控制参数设置较好时,电流波形的THD降至2.96%,电流波形得到较大的改善,说明阻尼控制参数对系统运行结果影响较大,加入阻尼控制并适当调整其控制参数可以较好的改善系统运行状态。

图17 加入阻尼控制前后的电流仿真波形Fig.17 Current simulation waveforms before and after damping control
4 结论
本文针对储能系统并网可能导致网络运行不稳定的问题,分析了风储并网系统在不同运行条件下的稳定性并提出相应的抑制策略。得到如下结论:
1)在风储并网系统中,风机转子侧内环电流环控制比例增益取较小值,储能逆变器电流环比例增益取较大值时,系统稳定性更高;风机转子侧内环电流环控制积分增益和储能逆变器电流环积分增益对系统稳定性的影响较小。
2)为了提高储能并网系统在弱电网条件下的谐波稳定性,提出一种基于入网电流反馈的有源阻尼控制方法,并对其反馈系数和截止角频率对运行结果的影响进行分析。结果表明,反馈系数采用较大取值,截止角频率采用较小取值时,更利于系统稳定。

