基于电压灵敏度的交直流电力系统静态电压安全域评估方法
陈 波,陈秋逸,郑富永,桂 睿,罗 琦,李宇骏
(1.国网江西电力科学研究院,江西南昌 330096;2.西安交通大学电气工程学院,陕西西安 710049;3.国网江西省电力有限公司,江西南昌 330077)
0 引言
近年来,特高压直流输电技术快速发展,我国已进入交直流混合的大电网时代[1-3]。特高压直流使电力系统安全特性发生重大改变[4-6],直流系统的功率调整可能导致直流近区电网潮流的不合理分布,造成节点电压越限的问题[7-8],而基于交流潮流的传统静态安全分析难以准确评估交直流混联的静态电压安全域[9]。因此探索适用于交直流系统的静态电压安全域评估方法,对提高交直流电力系统运行的安全性具有重要的意义。
目前已有大量文献研究了纯交流系统的静态电压安全域,刻画的方法大体上分为两类:逐点法和安全域法[10-11]。逐点法针对系统某一种预想事故进行潮流仿真计算,得出事故后的各项反映系统安全与否的指标[12-15]。但采用逐点法得出电压安全域需要进行大量潮流计算,不利于实时监控。针对这一问题,文献[16]通过系统正常运行方式下潮流计算得到的灵敏度矩阵,结合潮流方程的泰勒展开式导出了模拟电力系统断线的快速计算法,使静态安全分析向实用化更进一步。文献[17]根据泰勒展开式修正N网络的电压和灵敏度值从而得出N-1 网络的电压和灵敏度值。
针对逐点法的缺陷,国内外学者对安全域法也进行了大量研究[18-20]。安全域(Security Region,SR)法通过计算运行点安全域的边界表达式,对比当前运行点在安全域空间中的相对位置以实现对电力系统整体安全水平的评估。文献[19]对潮流方程雅克比矩阵行列式在临界点附近进行泰勒级数展开并保留二次项,得出了静态电压稳定域边界面的二次表达式,改善了线性近似方法的精度,但不便于在线应用。文献[20]在割集功率空间上,建立了静态电压稳定域的实用表达式。通过连续潮流搜索到一系列电压稳定临界点,用最小二乘法进行安全域边界的拟合,其误差可满足工程应用的要求。
文献[16-20]均适用于纯交流系统的静态电压安全域分析,但无法准确刻画交直流系统电压安全域。对此,文献[21-22]计及交直流系统各项约束条件,刻画了交直流系统的静态安全域,但并未给出当前工作点下具体的各节点电压安全运行范围,难以进行电压安全预防控制。
本文提出了一种适用于交直流混联系统的静态电压安全域的快速评估方法。首先对交直流系统各节点功率方程线性化,并求偏导数得到交直流混联系统中节点电压对节点注入功率、支路阻抗等的灵敏度,然后建立预想事故集,并将其中的事故相应等值为节点注入功率与支路阻抗的变化,从而利用灵敏度计算事故后节点电压变化量,最后基于事故后节点电压变化量评估静态电压安全域,给出明确的各节点电压安全运行范围。该方法仅需要计算扰动前状态下的灵敏度,提升了交直流系统电压安全域的评估速度。该方法的准确性在四机两区域的交直流混联系统及实际电网中得到验证。
1 交直流系统模型
1.1 直流系统准稳态模型
双端直流输电系统等效电路图如图1 所示,其中,Udi0,Udr0分别为逆变侧和整流侧换流变压器的阀侧空载电压;Udi,Udr分别为逆变侧和整流侧的直流电压;Rl为直流线路电阻;dxi,dxr分别为逆变侧和整流侧的等值换流电阻;β,α分别为逆变侧的触发超前角和整流侧的触发延迟角;Id为直流线路电流。

图1 直流输电系统等效电路Fig.1 Equivalent circuit of DC transmission system
根据图1 给出的直流输电系统的等效电路图,可由式(1)计算直流线路两侧的直流电压:

式中:γ为逆变侧关断角。
换流站交流母线电压与空载直流电压的关系为:
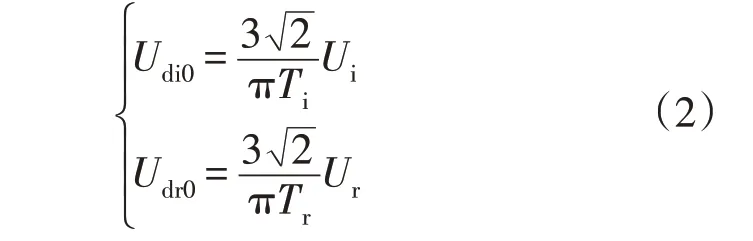
式中:Ui,Ur分别为逆变站和整流站的交流母线电压;Ti,Tr分别为逆变站和整流站的换流变压器变比。
直流线路逆变侧与整流侧的功率可表示为:

式中:Pdi,Qdi分别为逆变侧发出的有功功率和吸收的无功功率;Pdr,Qdr分别为整流侧吸收的有功功率和无功功率。
直流输电系统通常按照指定的功率运行,本文采用整流侧定电流和逆变侧定关断角的定功率控制模式,控制方程为:

式中:Ids为设定的直流电流参考值;γs为设定的逆变侧关断角参考值。
1.2 交直流系统潮流方程
由式(1)—式(4)可知,当换流站控制方式确定时,其注入功率为换流站交流母线电压幅值的函数[23]。因此,换流站交流母线可以作为PQ节点。
交流系统的功率平衡方程为:

式中:ΔPi,ΔQi分别为节点i的有功功率、无功功率误差;Ui为节点i的电压幅值;j为与节点i相连的母线节点;Pi,Qi分别为节点i的净注入有功和无功功率;Gij,Bij分别为线路ij的电导和电纳;θij为节点i与节点j的电压相角差。
对于换流站交流母线节点,需要在式(5)的基础上添加一项直流注入功率。对于整流站交流母线,其功率平衡方程为:

对于逆变站交流母线,其功率平衡方程为:

2 基于灵敏度的电压变化量计算方法
对于交直流混联的大规模电力系统,通过实时潮流计算来在线确定电压静态安全域有很大困难。为快速估算交直流混联系统的电压安全域,需得出基于灵敏度的电压变化量计算方法。
由式(5)、式(6)可知,当系统正常运行时,功率平衡方程可表示为[24]:

式中:W0为正常状态下的节点净注入功率向量;X0为正常状态下节点电压的幅值和相角组成的状态向量;Y0为正常状态下的网络参数。
当系统发生功率扰动ΔW或网络结构变化ΔY时,节点电压也必然发生变化ΔX,则式(7)变为:

将式(8)进行泰勒级数展开,并忽略二次项及高次项,整理得到计算节点电压变化量的线性模型:

2.1 功率波动
当系统发生功率波动但网络结构未发生改变时,ΔY为0,则式(10)变为:

式中:SW为节点注入功率对电压的灵敏度矩阵。
(X0,Y0)即潮流计算迭代结束时的雅可比矩阵J0,因此,SW可以很容易地通过对J0求逆获得。
2.2 网络结构变化
当系统网络结构变化而节点注入功率不变时,ΔW为0,则式(9)变为:

式中:SY为网络结构对电压的灵敏度矩阵。
若系统的总节点数为N,总支路数为b,导纳发生改变的支路两端节点为m,n,则(X0,Y0)为2N×b的矩阵。只有m,n节点的功率平衡方程会与支路mn的导纳有直接关系,因此该矩阵仅有4 个非零元素:

式中:bmn0为支路mn对地容纳的1/2;ymn为支路mn的导纳模值。
结合式(11)与式(12)得到电压变化量计算式:

3 静态电压安全域的快速计算法
为了计算交直流混联系统的静态电压安全域,基于系统正常运行状态下的潮流计算结果,对预想事故集中的所有高风险事故,如新能源出力波动、特高压直流闭锁、线路/主变N-1 故障等发生后可能出现的电压变化进行快速计算,得出最大电压变化量,根据规定的电压上下限确定各节点的电压安全域。
3.1 新能源出力波动
新能源发电具有弱抗扰性,其出力易发生大范围波动,影响电网稳定运行。新能源出力波动可用新能源接入节点的注入功率变化来表示:

式中:PW为新能源场站的功率的变化量,在ΔW中的位置对应于脱网的新能源场站接入的节点号。
由于网络拓扑并未改变,ΔY为0。将式(15)代入式(11)便可得到电压变化量的估算值。
3.2 直流闭锁
当交直流混联系统中的直流线路发生单级闭锁故障时,闭锁极消耗的无功功率瞬间降为0,而直流线路的无功补偿装置尚未切除,无功功率盈余注入交流电网,会造成系统电压升高,可能会导致电压越限。直流系统扰动对潮流方程的影响在于整流站和逆变站交流母线的注入功率变化。
单极闭锁后,假定非故障极立即启动1.2 倍过负荷能力,而无功补偿装置尚未切除,则直流电压变为原先的1/2,直流电流变为原先的1.2 倍,由式(3)可知,此时的直流功率可以近似表示为:

对比式(6),换流站交流母线的功率变化量可表示为:

式中:ΔPi,ΔQi分别为逆变站交流母线的有功和无功功率变化量;ΔPr,ΔQr分别为整流站交流母线的有功和无功功率变化量。由式(17),可以得到系统的注入功率变化:

网络拓扑没有变化,ΔY为0,将式(18)代入式(11)便可得到电压变化的估算值。
3.3 线路断线
当系统中某双回线发生一回线路断线故障时,此时网络结构发生了变化,ΔY中只有支路mn对应的元素为非零元素:

断线前后系统负荷并未发生变化,则有ΔW=0,将(20)代入式(12)便可得到电压变化的估算值。
35 kV 及以上供电电压正、负偏差绝对值之和不超过标称电压的10%[25],取电压的上下限为1.05 p.u.和0.95 p.u.。取预想事故集中系统各节点电压变化的最值,即可计算出各节点当前的电压安全域:

式中:ΔXimax,ΔXimin分别为节点i的电压变化最大值和最小值;Uimax,Uimin分别为节点i的安全运行上下限。
图2 给出了本文所提静态电压安全域评估方法的实施流程。

图2 所提的电压安全域计算流程Fig.2 Calculation process of proposed voltage safety region
4 仿真分析
为了验证本文所提基于灵敏度的快速计算法替代求解潮流估算系统电压变化的可行性,在Matlab 中对4 机11 节点的交直流混联系统和9 机48 节点的江西500 kV 交直流混联系统进行仿真验证。
4.1 四机两区域交直流混联系统算例
四机两区域的交直流混联系统示意图如图3所示。

图3 测试交直流混联系统示意图Fig.3 Outline of AC/DC hybrid test system
交流电网包含4 台等值发电机G1—G4,并在节点1 接入1 台等值风力发电机组WT1,负荷采用恒功率模型,并通过RX 模型表示的输电线路与发电机连接。直流输电线路位于节点3 和节点5 之间。测试系统的主要参数如表1 所示。

表1 测试系统主要参数Table 1 Test system main parameters
表2 给出了系统发生新能源出力波动、直流闭锁和线路断线3 种故障时,利用灵敏度计算法得到的系统各节点电压变化量与重新计算潮流得到的实际电压变化的对比,并给出了两种计算方法的绝对误差。由表2 可知,灵敏度计算法所得ΔU与实际电压变化量的平均误差为0.000 8 p.u.,对于各故障中变化量较大的节点电压可以给出较准确的估算。基于灵敏度的电压变化量计算方法可以保证足够精度的基础上节省重新求解潮流的时间,提升静态电压安全域的评估速度。

表2 测试系统各节点电压变化灵敏度计算法结果Table 2 Voltage variation of each node of the test system calculated by sensitivity calculation method p.u.
4.2 江西电网算例
为了验证本文所提快速计算法在实际电网中的可行性,进一步在江西电网500 kV 网架上进行了测试。图4 为±800 kV 雅中直流馈入江西电网,输送有功功率6 000 MW。

图4 江西电网500 kV系统拓扑图Fig.4 Topology of 500 kV system in Jiangxi power grid
特高压直流输电投运后,对近区电网的无功电压有较大影响,因此监测特高压直流近区的节点电压尤为重要。利用灵敏度计算法得到系统在3 种故障下的节点电压变化量ΔU,如表3 所示,灵敏度计算法所得ΔU与实际电压变化之间的平均误差为0.001 3 p.u.。因此基于灵敏度的电压变化量计算法对于直流近区节点电压变化计算较为准确,故采用电压变化量计算出的静态电压安全域可以有效保证系统电压不越限。

表3 系统近区电压变化灵敏度计算法结果Table 3 Voltage variation in system near zone calculated by sensitivity calculation method p.u.
5 结语
本文针对交直流混联电力系统,提出了一种基于灵敏度分析的静态电压安全域评估方法。首先,基于直流准稳态模型得到交直流混联系统潮流方程;其次,通过对功率方程线性化得到节点功率与支路导纳对于节点电压的灵敏度,并进一步得到基于灵敏度的电压变化量计算方法;最后,对事故进行等值,计算节点电压变化量的最大值和最小值从而得到各节点的静态电压安全域。经过仿真分析,验证了所提基于灵敏度的快速计算法可以取得很好的精度,能在电网实际运行中在线评估静态电压安全域,为电压安全预防控制实时提供参考。

