基于改进GSA-SVM模型的电力变压器故障诊断

咸日常，范慧芳，李 飞，高鸿鹏，陈 蕾

（1.山东理工大学电气与电子工程学院，山东淄博 255049；2.国网山东淄博供电公司，山东淄博 255049）

0 引言

近年来，随着我国电网规模、装机容量与发电量的不断增加，电力变压器数量日益增多、单台容量不断增大，其故障率也呈上升趋势，已逐步威胁到整个电力系统的稳定运行[1-2]。因此，准确高效地评估变压器运行状态，及时发现内部潜在故障，对保障电网安全运转具有重要意义[3]。

目前油中溶解气体分析（Dissolved Gases Analysis，DGA）技术发展已较为成熟[4]，以DGA 技术为基础，一些传统的诊断方法如IEC 三比值法、改良三比值法、四比值法及图解法等被应用在实际变压器故障诊断中，但这些传统的诊断方法也不可避免地存在某些缺陷，如使用条件受限、比值编码不全等[5-6]。随着智能算法的发展，大多数学者开始采用DGA 诊断结果与智能诊断方法相结合的方式来提高变压器故障的预测准确率。常见的智能诊断方法有BP 神经网络[7]、极限学习机[8]及支持向量机（Support Vector Machine，SVM）模型[9]等。赵文清等人考虑到BP 神经网络到达一定深度时，其诊断性能会趋于饱和，故提出残差BP 神经网络方法，结果表明该模型在小样本数据下仍能保持较好的预测能力[10]。采用SVM 模型进行故障诊断时，模型中核函数和惩罚因子限制了其分类性能，若取值不当会导致预测结果产生较大误差，故各种仿生物优化算法[11-13]被引入，以提高SVM 模型对变压器故障的预测能力。

综上，本文提出一种新的电力变压器故障诊断模型，即改进引力搜索算法优化的SVM 模型，以提高变压器故障诊断的准确率。首先利用混沌序列改进传统GSA 算法，达到混沌群体粒子初始位置、保持群体多样性的目的；然后将改进后的GSA 算法用于SVM 模型中，以提高电力变压器故障识别准确率。最终预测结果表明，改进GSA-SVM 模型有着更高的预测准确率，可有效应用于油浸式电力变压器内部故障的诊断。

1 多分类支持向量机

SVM 是由Vapnik 等人于1995 年提出的一种二分类模型，其目的是寻找一个超平面对待分类样本进行合理划分[14]。

对于线性可分的待测样本，可行的分类超平面可能有多种如图1 所示，其中横、纵坐标表示样本个数。从图1 可以看出，2 类待分类样本集之间的分割线可以有多条，但与L1 和L3 相比，L2 作为2类样本的分类超平面更合适，原因是其与所有的分类样本间隔更大，因此测试样本集被错误划分的概率更小，即符合最大化间隔的原则。

图1 二分类超平面Fig.1 Two-class hyperplane

求解标准SVM 模型最优分割超平面问题可以表示为：

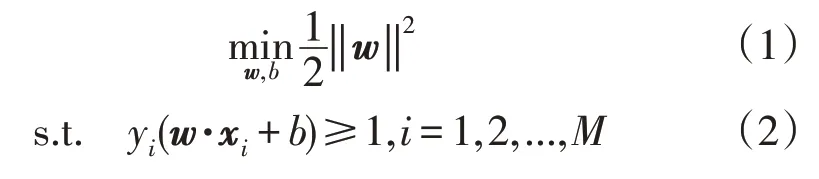
式中：w，b分别为最优分割超平面的法向量和截距；yi∈{- 1,1} 为类标记，表示负类与正类；xi为给定的输入数据。

首先将式（1）转化为无约束的拉格朗日目标函数，利用拉格朗日函数的对偶性辅助求解。对于线性可分SVM 模型，所构造出的凸二次规划问题可表示为：

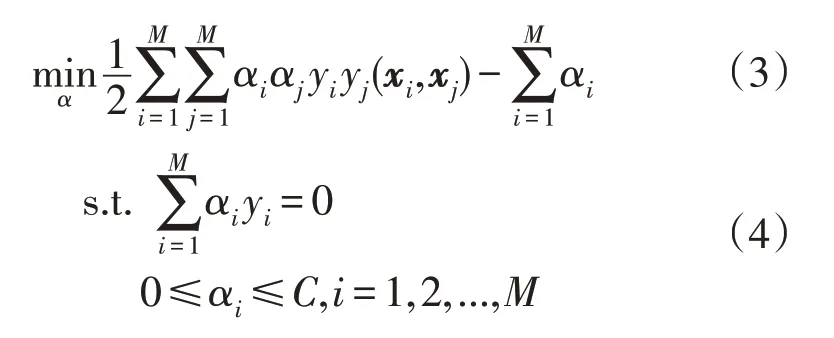
式中：α为拉格朗日乘子；(xi,xj)为训练数据集；C为惩罚因子。

根据式（3）和式（4）可求得拉格朗日乘子的最优解α*，然后可进一步求解最优分割面的法向量w，如式（5）所示：

选取α*中的任一分量，使其满足式（4）的约束条件，计算并求解b*，如式（6）所示：

根据分类决策平面w*·x+b*=0 可得决策函数（fx）如式（7）所示：

对于输入空间中的非线性问题，可通过非线性变换将其转化为某一维特征空间中的线性分类问题，因此文中引入核函数K(x,xi)来代替目标函数与分类决策函数中的内积，故非线性支持向量机的分类决策函数变为：

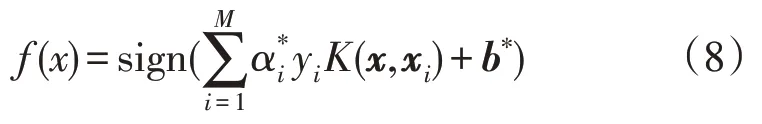
最常用的核函数为高斯核函数，这种函数不仅可以体现出样本到更高维空间的映射关系，且本身所含参数少，性能比较稳定，表达式如下：

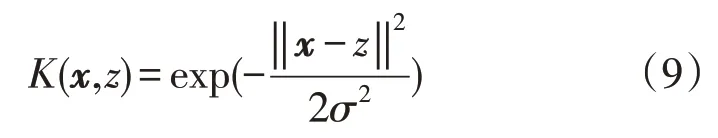
式中：σ为函数的宽度参数，σ＞0；z为高斯核函数中心。

从式（3）—式（9）推导可以看出，SVM 模型的最优分割超平面与惩罚因子C和宽度参数σ有关，故需要对二者进行参数寻优，从而提升SVM 的分类诊断性能。

2 改进的引力搜索算法

2.1 传统引力搜索算法

引力搜索算法（Gravitational Search Algorithm，GSA）是从万有引力定律与牛顿第二定律中所引申出的一种智能优化算法[15-16]。在传统GSA 中，待优化问题的可行解用每个粒子的坐标来表示，粒子的质量代表适应度。设种群中共有N个粒子，粒子p用向量表 示，其 中p∈{1 ,2,...,N}，n为待求解的维度，为粒子p在第v维空间中的坐标。在第u次迭代中，粒子q在第v维空间对粒子p的引力可表示为：

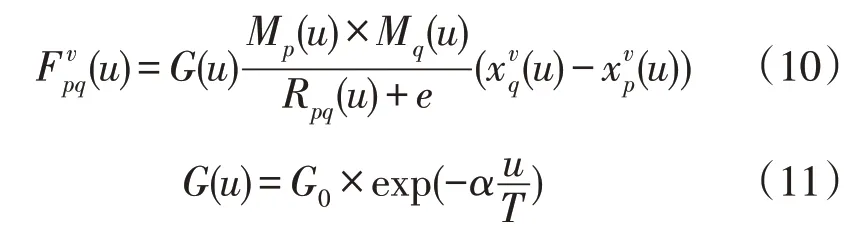
式中：G(u)为第u次迭代时刻的引力常数；G0为初始时刻引力常数，其值为6.754×10-11N·m2/kg；α为常量，本文取值为20；T为最大迭代次数；Rpq(u)为在第u次迭代时粒子p与q之间的距离[17]；e为一个非常小的常量，本文取值为0.01；Mp(u)为粒子p的质量，由其适应度值根据以下公式得到：

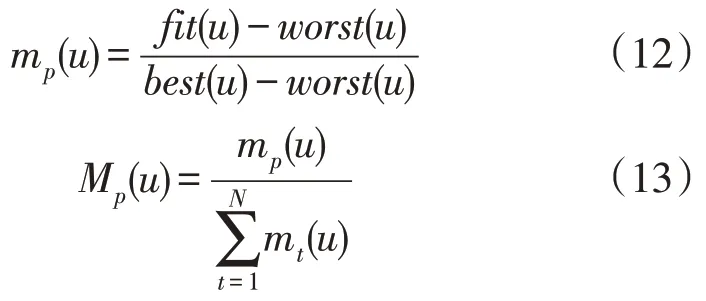
式中：fit(u)为粒子p在第u次迭代时的适应度；worst（u），best（u）分别为在第u次迭代时所有个体中最差适应度函数值和最优适应度函数值；mp（u）为粒子p第u次迭代的质量。

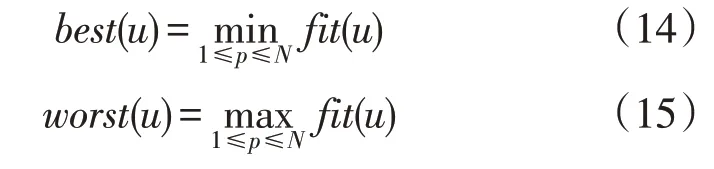
第u次迭代后，粒子p在第v维空间中所受到的合力可表示为：

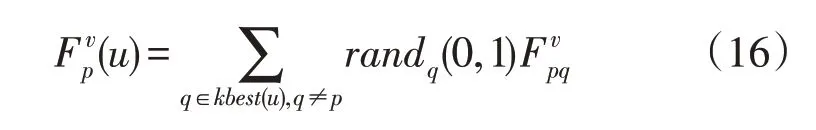
式中：rand为[0，1]之间的一个随机数；kbest为个体质量按降序排在前k个的个体，并且k的取值随迭代次数线性减小。

在万有引力作用下，根据牛顿第二定律可得粒子p在第v维空间中的加速度如式（17）：

粒子位置更新策略为式（18）：

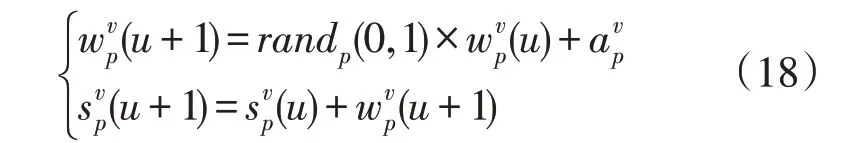
式中：为粒子p在第v维空间的速度；为粒子p在第v维空间的位置。

GSA 算法通过确定粒子间万有引力、加速度、各粒子质量以及更新粒子位置坐标这一迭代过程来不断探索最优解。

2.2 改进策略

传统GSA 算法收敛速度较慢、全局寻优能力也较差，故会导致最终预测准确率较低。考虑到混沌序列的随机性、规律性特点，本文提出一种基于混沌序列改进的GSA 优化算法，利用混沌序列本身的遍历性达到初始化群体粒子的目的，使得初始个体尽可能地均匀分布在整个求解空间中，以提高初始解的质量，可有效避免局部最优情况，在保持群体多样性的同时还可以提升寻优精度。

采用目前广泛使用的如式（19）所示的Logistic方程构成混沌序列，以提升算法的全局寻优能力。

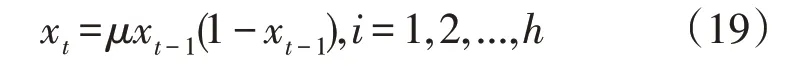
式中：μ为混沌状态的控制参量，本文取值为4；xt-1为t-1 维的混沌重力粒子。

混沌初始化群体粒子位置的具体步骤如下：

1）随机产生1 组t维序列作为一个初始混沌重力粒子x0。

2）将x0代入式（19）中进行迭代，直至到达最大迭代次数时停止。最终产生K个混沌粒子，分别计算其适应值。

3）从步骤2）中所产生的K个混沌粒子中选出最优的k个粒子构成kbest集合，作为GSA 算法初始群体粒子。

2.3 性能比较

为了验证本文所提改进GSA 算法性能的优越性，选取一种最小值为0 的测试函数Sphere 函数进行算法性能的评估，并与传统的GSA[18]、蜂群算法（Artificial Bee Colony Algorithm，ABC）[19]及粒子群算法（Particle Swarm Algorithm，PSO）[20]进行比较分析。利用所述4 种优化算法对Sphere 测试函数在Matlab中进行性能测试，所得到的仿真结果如图2 所示。

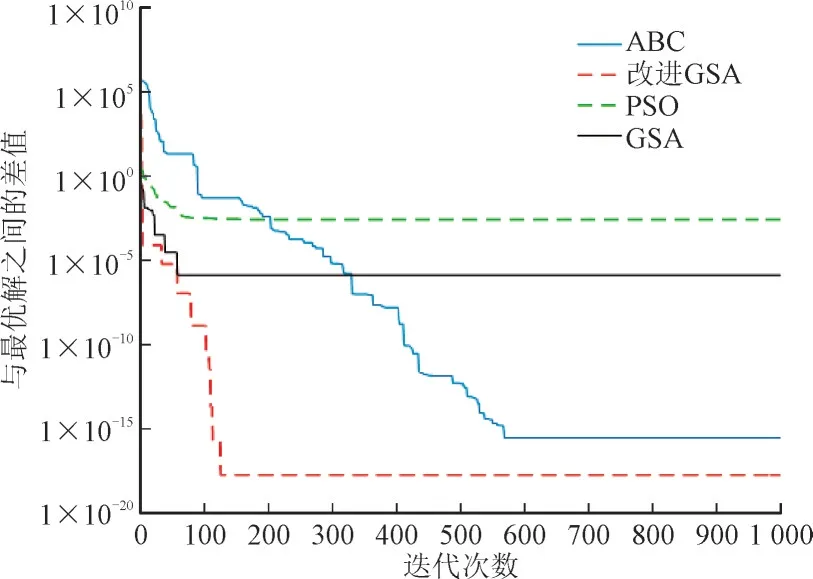
图2 不同优化算法寻优性能对比图Fig.2 Comparison chart of optimization performance with different optimization algorithms

从图2 可以看出，改进GSA 优化算法与其他3种优化算法相比，无论是在收敛性方面还是在全局寻优性能方面，都表现出较为良好的优化效果。故本文选取改进的GSA 算法对SVM 模型的参数C和σ进行优化，进而提升模型本身的分类准确率。

3 基于改进GSA-SVM 模型的电力变压器故障诊断

3.1 基于改进GSA优化的SVM模型

为准确预测电力变压器各类故障，文中将SVM模型中2 个待优化参数的搜索范围都设置为[0.01，100]，群体粒子总数设置为20，最大迭代次数设置为100。利用改进GSA 算法对SVM 模型进行优化的算法流程图如图3 所示，具体步骤如下：

图3 基于改进GSA-SVM模型算法流程图Fig.3 Algorithm flow chart based on improved GSASVM model

1）设置最大迭代次数、群体中粒子总数目及待求解的个数与维度等。

2）利用混沌序列初始化重力群体粒子。

3）检查种群中粒子越界情况并按照目标函数计算各粒子的适应度值。

4）利用公式计算各粒子的万有引力及质量。

5）计算各粒子所受总引力，更新粒子加速度和位置。

6）判断是否满足终止要求，若满足则输出最优解，若不满足则返回步骤3。

7）根据最优解建立SVM 模型，输入训练数据对模型进行训练。

8）训练完毕后，将预测数据输入进行预测，预测完成后输出最终结果。

3.2 电力变压器故障诊断

在阅读文献[21-24]以及总结大量变压器油色谱故障样本的基础上，文中选取了H2，CH4，C2H4，C2H6和C2H2共5 种典型气体作为故障特征气体[25-26]，采用改进GSA-SVM 模型实现电力变压器故障性质的预测[27-29]。将变压器故障按照性质分为6 种，具体类型及对应编码如表1 所示。

表1 故障类型与编码对照表Table 1 Comparison table of fault types and codes

从山东电网收集了包含6 种故障类型的286组电力变压器故障油色谱分析数据，选取其中的250 组故障数据作为改进GSA-SVM 模型的训练数据，剩余36 组作为该模型的预测数据。训练数据和预测数据的分布情况如表2 所示。

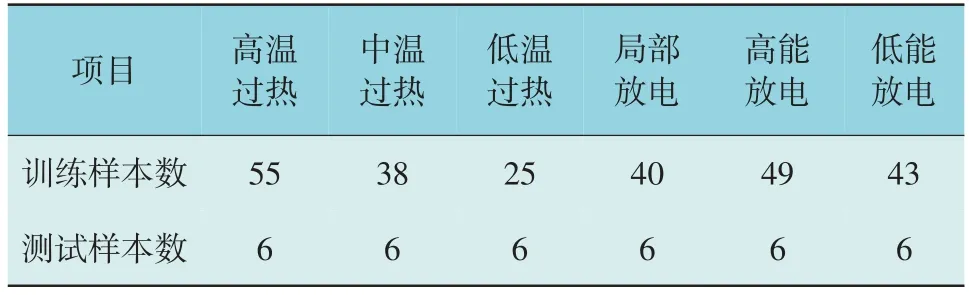
表2 训练样本与测试样本分布情况Table 2 Distribution of training samples and test samples 组

首先利用改进GSA 算法优化的SVM 模型对所选出的训练样本进行预测，其故障类型的预测结果如表3 所示。

表3 6种故障类型训练样本的预测结果Table 3 Prediction result of 6 types of training sample

从表3 中可以看出，利用改进GSA 算法优化的SVM 模型对训练数据的预测结果都可以保持在一个较高的准确率，再次验证了改进GSA 算法在SVM 模型中的可行性。

利用本文改进GSA 算法优化的SVM 模型对电力变压器故障性质进行预测诊断，同时将预测结果与ABC-SVM，PSO-SVM 及传统GSA-SVM 模型所预测得到的结果进行对比分析。在Matlab 环境下分别对这4 种情况进行仿真预测，最终得到的各模型分类预测结果如图4—7 所示，各模型最终分类准确率汇总见表4。

表4 不同方法的分类准确率对比表Table 4 Comparison table of classification accuracy of different methods %

图4 PSO-SVM模型预测结果Fig.4 Prediction results of PSO-SVM model

从图4 可以看出，利用PSO-SVM 模型对36 组预测数据进行预测后，错误样本共10 个，其中故障为低温过热与低能放电的错误分类样本较多，二者的分类准确率仅为50%和33.3%，利用该模型进行预测的最终综合准确率为72.2%。

从图5 可以看出，利用ABC 算法优化后的SVM 模型对预测样本进行预测，局部放电故障的准确率相对较低，其综合预测准确率为88.9%，与PSO-SVM 模型相比，其准确率提高了16.7%，说明ABC 算法与PSO 算法相比，前者具有更好的全局寻优能力。

图5 ABC-SVM模型预测结果Fig.5 Prediction results of ABC-SVM model

从图6 可以看出，利用传统的GSA-SVM 模型对36 组预测数据进行预测，错误分类样本有5 个，原因可能是模型在训练时群体粒子未能均匀分布在整个求解空间中，模型在训练时陷入了局部最优区域，出现了过拟合现象，故未能充分学习，从而导致预测准确率较低。

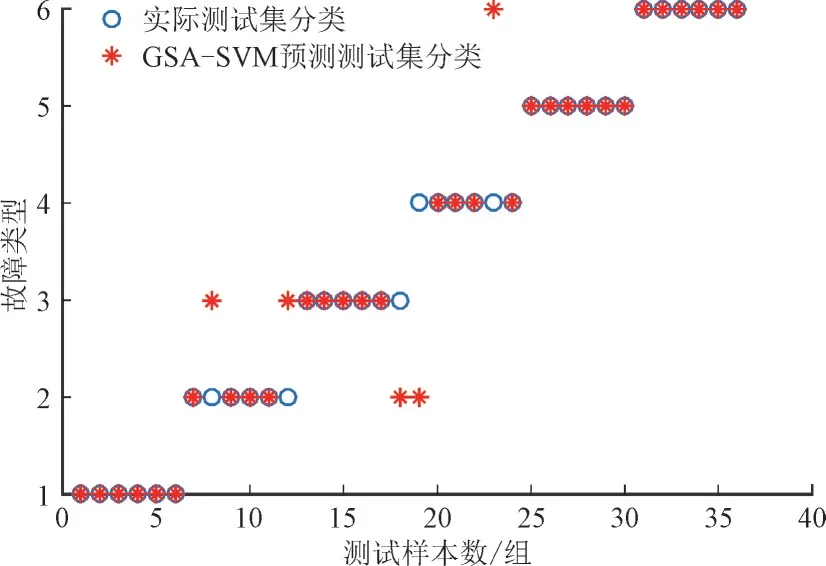
图6 GSA-SVM模型预测结果Fig.6 Prediction results of GSA-SVM model

从图7 可以看出，采用混沌序列优化后的GSA-SVM 模型对测试集进行预测，错误样本仅为2个，其中高温过热、低温过热、高能放电及低能放电4 种故障的预测准确率达到100%。综合故障诊断准确率高达94.4%，比未改进前的GSA-SVM 模型预测准确率提高了8.3%。

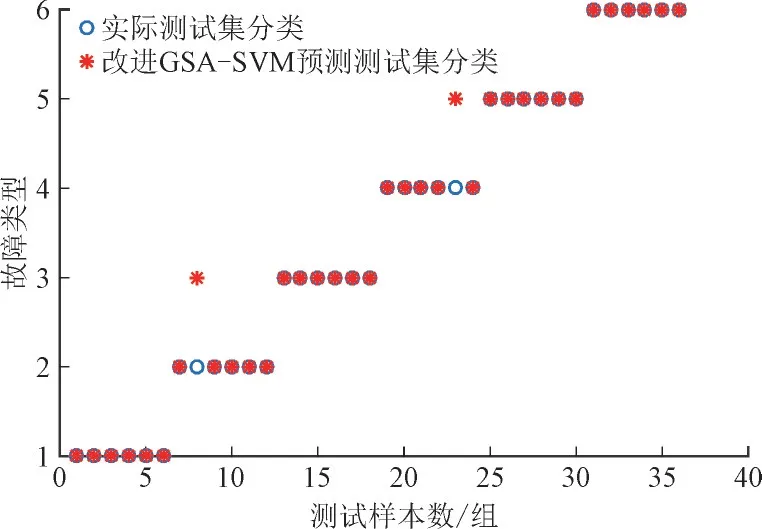
图7 改进GSA-SVM模型预测结果Fig.7 Prediction results of improved GSA-SVM model

综上所述，将混沌序列引入GSA 算法，再将之用于SVM 模型中对其参数进行优化，最终得到的改进模型与传统ABC 算法、PSO 算法、GSA 算法优化SVM 得到的模型相比，具有更高的电力变压器故障预测准确率。

4 结语

本文首先将传统的GSA 算法利用混沌序列进行改进，增添了群体粒子的多样性，使得全局寻优能力更强。接着将改进后的GSA 算法用于SVM 模型中，从而优化其本身的参数，提高了模型诊断预测准确率。最后将文中所提的改进模型与传统GSA-SVM，PSO-SVM 和ABC-SVM 模型的仿真预测结果进行了对比分析，最终发现利用混沌序列优化的GSA-SVM 模型预测准确率更高，可较好地保证变压器故障诊断的准确性，为电力检修人员及时发现内部潜伏性故障提供一定的参考。