基于已有充电站调整的电动汽车充电站选址研究

高治佳，李星梅，贾冬青，王玉玮

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学经济管理系，河北保定 071000）

0 引言

作为燃油车辆的理想替代品，电动汽车以其低污染、低排放、高能源利用率等优势在市场上迅速崛起[1-3]。据公安部统计，截至2021 年底，我国电动汽车保有量已经达到640 万辆。国家“十四五”规划提出“要进一步加快壮大新一代新能源汽车产业的发展”，这意味着未来几年我国电动汽车数量将会持续增长[4-6]。考虑到我国已经形成基本的充电设施服务网络[7]，新一轮充电站选址规划需要考虑已有充电站的位置和容量，避免重复投建[8]、增加电网负荷[9]。电动汽车行业仍处于发展阶段，充电基础设施建设存在缺口是限制其发展的因素之一[10-14]。现有充电站服务供给难以满足用户日益增长的充电需求[15]，合理进行充电站选址规划成为当前亟待解决的问题。

目前，国内外关于充电站选址问题的研究均未考虑对区域内已有充电站的调整。文献[16]在考虑充电站的容量、覆盖范围和充电便利性等因素的基础上，构建了新充电站选址模型。文献[17]研究在续航里程约束下的电动汽车交通流量均衡和最优充电站选址问题，忽略了已有充电站对新充电站规划的影响。文献[18]分析了基于不确定环境的高速公路光储充电站选址定容问题，没有考虑已有充电站的位置和容量。然而在项目组合选择领域，关于已有项目对新项目选择个数影响的研究已经引起了广泛关注。文献[19]明确指出动态项目组合选择问题既需要考虑新的备选项目，又需要考虑企业已有的旧项目。文献[20]把已有项目的状态分为放弃、保持原状和更新规模3 种情况，通过收益、成本等参数来控制项目更新规模。在文献[19-20]研究基础上，文献[21]提出了考虑企业已有项目的新型“动态主动打断项目组合选择”模型，将旧项目对新项目选择的影响反映在项目收益上。

由于充电站选址问题的特殊性，考虑已有充电站调整的电动汽车充电站选址问题比同时考虑新旧项目的项目组合选择问题更为复杂。因此本文基于已有研究成果，构建了一种全新的考虑已有充电站调整的电动汽车充电站选址模型。通过引入中间变量构造分段非线性函数来描述已有充电站和新建充电站之间的关系，并将该模型应用于某地区电动汽车充电站选址案例中，通过仿真验证了所构建模型的可行性和有效性。

1 充电站选址分析

为研究考虑已有充电站调整的电动汽车充电站选址问题，本文假设区域内已经存在m个充电站，规划者需要考虑是否调整已有充电站。与此同时，有n个候选点可供建设新的充电站，规划者需要根据用户充电需求确定新充电站的数量、位置和等级。

1.1 充电站规划

本文根据充电站选址特性结合项目组合选择中对已有项目的处理办法，将充电站选址规划分为拆除、更新和新建充电站3 种情况。其中更新包括升级和降级，维持现状可理解为升级级别为0。所引入中间变量vj为：

式中：和均为0-1 变量，分别表示规划点j在规划后和规划前是否存在充电站；J为充电站规划点集合。

由式（1）可得，vj∈{ }-1,0,1 。当vj=-1时，表示可以将规划点j的充电站拆除；当vj=1 时，表示可以在规划点j新建充电站；当vj=0 时，表示可以更新规划点j的已有充电站。

1.2 规划成本

充电站的规划成本包括已有充电站的调整费用和新建充电站的建设费用。对于规划点j，会产生拆除费用、更新费用和新建费用3 种相关成本，其中更新费用包括升级产生的成本和降级获得的回收资金。规划点j的规划成本为：

式中：为规划点j的规划成本；和均为0-1变量，分别表示规划点j在规划前和规划后是否存在s等级的充电站；DIs为拆除s等级的充电站获得的残值；C1和C2分别为已有充电站升级产生的成本和降级获得的回收资金；μj为规划前后规划点j的充电站等级变动情况；Cs为s等级充电站的建设成本；S为充电站等级集合。

当μj>0 时，规划点j的已有充电站将被升级，升级产生的成本为C1μj；当μj<0 时，规划点j的已有充电站将被降级，降级所获得的回收资金为C2μj；当μj=0 时，规划点j的充电站等级保持不变，既不会产生成本也不会获得回收资金。

1.3 网损成本

配电网由多个电网节点组成，由于每个节点的负荷能力不同，当不同等级的充电站接入后会对配电网造成不同的网络功率损耗[22-23]。与1.2 节规划成本计算方式相同，在拆除、更新和新建充电站3种情况下规划点j的网损成本为：

式中：为规划点j的网损成本；Qs为s等级充电站日服务能力；g为每台充电桩的线路和充电损耗总和；pˉ为平均电价。

1.4 运营成本

充电站的运营成本主要包括设备维护费用、员工工资和其他材料费用等。考虑到新旧充电站的维护成本不同，本文通过给新建充电站的运营成本乘以一个系数来得到已有充电站的运营成本。规划点j的运营成本为：

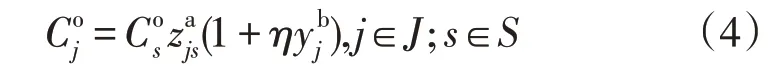
式中：为规划点j的运营成本；为s等级充电站的运营成本；η为比例系数。

2 充电站选址模型构建

2.1 目标函数

考虑到充电站规划者和电动汽车用户的利益，本文以最小化充电站投资总成本和用户充电总距离的综合偏离函数作为模型的目标函数。投资总成本偏差和充电总距离偏差分别为：

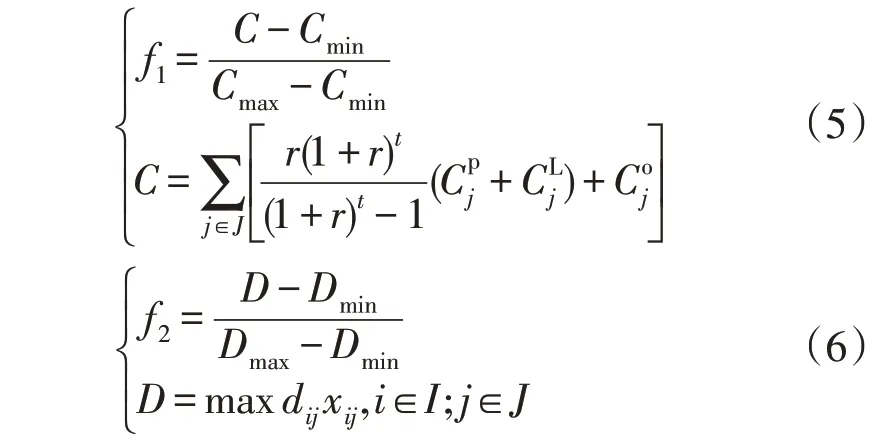
式中：f1为投资总成本偏差；C为投资总成本；Cmin和Cmax分别为最小投资总成本和最大投资总成本；r为贴现率；t为充电站的使用寿命；f2为充电总距离偏差；D为充电总距离；Dmin和Dmax分别为最小充电总距离和最大充电总距离；dij为用户从需求点i到规划点j所要行驶的距离；xij为0-1 变量，表示需求点i的用户是否到规划点j进行充电。

基于已有充电站调整的电动汽车充电站选址模型的投资总成本和充电总距离最小化目标函数为：

式中：f为投资总成本和充电总距离的综合偏离函数；α和β分别为投资总成本和充电总距离的偏离权重系数。

2.2 约束条件

1）容量约束。由于需要充电的电动车辆数量不得超过该充电站的容量，设置模型的容量约束为：

式中：wi为需求点i处需要充电的电动汽车的数量；I为电动汽车用户充电需求点集合。

2）功率约束。由于需要充电的电动汽车总功率不得超过该充电站所能接入的最大功率，设置模型的功率约束为：

式中：δi为需求点i处的电动汽车正常运行时的功率；ℓ 为每台充电桩的额定功率。

3）预算约束。由于充电站的投资总成本不能超过初始投资预算，设置模型的预算约束为：

式中：W为初始投资预算。

4）服务范围约束。由于需求点i必须在规划点j的服务半径之内，才可方便用户到j点进行充电，设置模型的服务范围约束为：

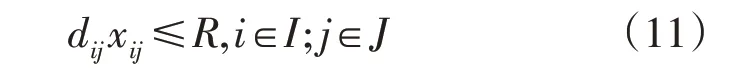
式中：R为用户所能接受的最远充电距离。

5）用户充电行为约束。只有当规划点j建有充电站时，用户才可以到j点进行充电，设置模型的用户充电行为约束为：

6）用户充电唯一性约束。由于每个需求点i的电动汽车只能选择1 个充电站进行充电，设置模型的用户充电唯一性约束为：

7）充电站唯一性约束。由于每个规划点j最多建设一种等级的充电站，设置模型的充电站唯一性约束为：

综上所述，基于已有充电站调整的电动汽车充电站选址模型为：

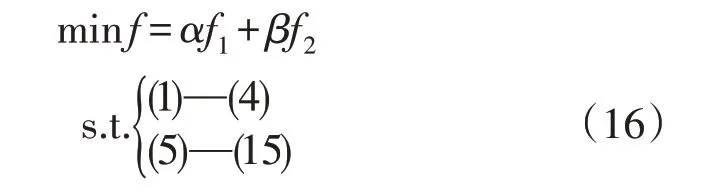
3 仿真分析

3.1 场景设置

为验证本文所构建模型的合理性和有效性，本节选取某地区电动汽车充电站选址项目作为研究对象，其需求点和充电站规划点数据均来自参考文献[24]。在该仿真实验中，设充电站的建设分为4 个等级（数字越大等级越低），每个等级中充电站的建设成本和服务能力参考文献[25]。本文假设投资总成本和充电总距离的偏离权重系数均为0.5。每上升一级，改造成本增加5.01×105元，各等级充电站的运营成本和拆除收益分别为其建设成本的10%和5%[25]，充电站的服务半径为3 km，运行年限为20 年，贴现率为8%，充电单价为1.2 元/kWh，电动汽车单次充电电量为40 kWh[24]，单台充电桩功率为96 kW[26]，初始预算为2.0×107元。

为验证本文所建模型的优势和求解结果，设计2 种场景进行分析和比较。场景1：在相同的容量水平下，既考虑已有充电站的拆除和更新，又考虑新建充电站选址的模型；场景2：在相同的容量水平下，不考虑已有充电站，不涉及已有充电站的调整成本和新旧充电站运营成本的差异，对所有的规划点重新规划的模型。

3.2 对比分析

分别对场景1 和场景2 中的模型进行求解，并对结果进行对比分析，进一步验证本文所建模型的优势。场景1 和场景2 下各项成本对比如表1 所示。

表1 场景1和场景2下各项成本对比Table 1 Cost comparison for scenarios 1 and 2 元

由表1 可知，对比规划成本，场景1 远低于场景2，原因在于场景1 中对已有充电站做出合理的更新改造，通过拆除部分已有充电站获得回收资金冲抵了部分规划成本。对比网损成本，二者相差1.12×105元，说明场景1 更有优势。对比运营成本，场景1 高于场景2，原因在于已有充电站已使用一段时间，相对于新充电站运营维护难度较大，运营成本较高。对比总成本，场景1 比场景2 节约21.95%的总成本，且充电站的使用寿命一般为15—20 年，从长期发展的角度来看，场景1 的优势更加突出。

在场景1 和场景2 下分别对某地区C1—C15共15 座充电站规划点进行选址分析，通过模型求解得到每种场景下的建站数量、位置和等级。规划前后2 种场景下充电站选址结果如图1 所示。

图1 规划前后2种场景下充电站选址结果Fig.1 Site selection results of charging stations in two scenarios before and after planning

由图1 可知，场景1 与规划前相比，拆除了C1和C6 规划点的充电站，C12 和C15 规划点的充电站等级不变，C2 规划点升级为2 级充电站，C4 规划点升级为3 级充电站，在C7 和C13 规划点新建1级充电站，在C8 和C11 规划点新建3 级充电站。场景2 与规划前相比，在C7，C12 和C15 规划点新建1 级充电站，在C4 规划点新建2 级充电站，在C8，C11 和C13 规划点新建3 级充电站，在C2 规划点新建4 级充电站。是否在规划点建设充电站是由规划点位置和用户充电需求点位置共同决定的。因为规划点C1，C3，C5，C6，C9，C10 和C14 距离用户充电需求点过远，超出用户所能接受的最远充电距离，所以在2 种场景下均没有建设充电站。整体来看，规划后2 种场景均选择在C2，C4，C7，C8，C11，C12，C13 和C15 共8 个规划点更新和新建充电站，场景1 中尽最大限度对已有充电站进行了更新，新建充电站数量较少，从而降低了规划成本。

以东经121.458 3 °，北纬31.241 6 °为坐标原点，建立xy坐标系，得到已有充电站规划点、新建充电站候选点和用户需求点的坐标，场景1 和场景2下坐标x，y对应的充电站规划连接拓扑示意图如图2 所示。

图2 充电站规划连接拓扑示意图Fig.2 Schematic diagram of connection topology for charging station planning

由图2 可知，2 种场景下充电站C7，C8 和C11的服务节点完全相同，如果不考虑已有充电站的调整，将选择在规划点C2，C4，C12 和C15 建设充电站，然而规划前这4 个候选点已经存在不同等级的充电站，所以选择在现有基础上进行更新改造，可有效减少规划前期的投资成本，实现资源的合理利用。

通过对场景1 和场景2 规划后的选址结果进行对比可知：（1）在考虑已有充电站调整的场景1中，虽然运营成本高于不考虑已有充电站的场景2，但场景1 的规划成本、网损成本和总成本更低，说明在充电站选址过程中考虑已有充电站有利于节约成本；（2）场景1 中对已有充电站做出了合理的调整，对满足条件的充电站进行更新改造，拆除多余的充电站。这样既可以避免现有资源的浪费，也可以节约投资成本，对电动汽车充电站选址问题具有指导意义。

3.3 敏感性分析

由于本文的优化目标是最小化综合偏离函数，成本偏离权重系数α的取值将直接影响最终的选址结果。本节将在其他条件不变的前提下对不同α下生成的子模型进行求解，不同α下模型输出值如表2 所示。

表2 不同α 下模型输出值Table 2 Model output values under different α

不同α下总成本和充电总距离变化趋势如图3所示。

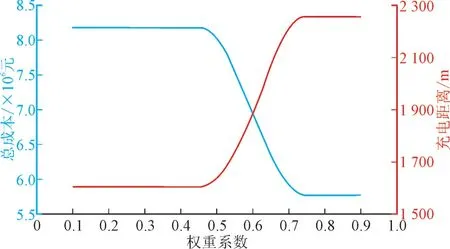
图3 不同α 下总成本和充电总距离变化趋势Fig.3 Variation trend of total cost and charging distance under different α

不同α下的选址结果如图4 所示。

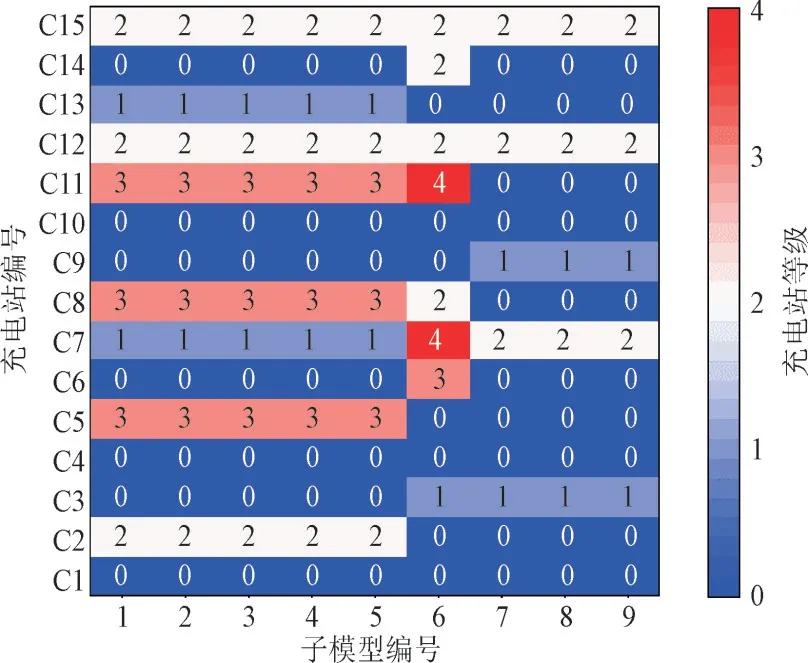
图4 不同α 下的选址结果Fig.4 Site selection results under different α

由图3 和图4 可知，当α在0.1～0.5 之间变化时，子模型求解的总成本和充电距离趋于稳定，在此范围内选址结果没有变化；当α在0.5～0.7 之间时，随着α的增加，总成本在逐渐降低，同时充电距离在逐渐增加；当α由0.7 增加到0.9 时，总成本和充电距离再次趋于稳定，选址方案不变。

通过敏感性分析可知：（1）当规划者更注重减少充电距离时，应该选择对已有充电站进行更新，充分利用已有充电站内的设施和土地资源；反之，当规划者更注重降低总成本时，则可以选择对已有充电站进行拆除，减少充电站数量；（2）不同权重系数配置下的决策结果虽然不具备直接比较的意义，但能为规划者提供更多的选址思路，帮助规划者做出科学合理的决策。

4 结论

在充电站选址领域，现有研究忽略了已有充电站对电动汽车充电站选址的影响。本文根据充电站选址问题的特性并结合项目组合选择的思想，构建了考虑已有充电站调整的电动汽车充电站选址模型。并将该模型应用于某地区电动汽车充电站选址案例中，仿真结果表明：

1）在电动汽车充电站选址过程中考虑已有充电站的调整，可以有效减少规划前期的投资成本，实现资源的合理利用。

2）已有充电站调整类型和新充电站选择方案与规划者对充电距离和成本的偏好程度有关。