Spin transport properties in ferromagnet/superconductor junctions on topological insulator
Hong Li(李红) and Xin-Jian Yang(杨新建)
College of Science,China University of Petroleum,Qingdao 266580,China
Keywords: TI-based FM/SC junctions, magnetic gap effect, Andreev retro-reflection, specular Andreev reflection
1. Introduction
Andreev reflection (AR)[1]is an important phenomenon in superconducting tunnel junctions, through which the dissipative electrical current can converse into non-dissipative supercurrent. Recently, Beenakker[2]predicted that two different types of AR may happen in graphene superconducting junctions. Usually, reflected hole at the normal metal/superconductor(NM/SC)interface goes back along the path of the incident electron. This process is called Andreev retro-reflection.[3]In undoped graphene, however, the reflected hole may travel like the normal reflected electron which is called specular AR. The specular AR process is absent in ordinary NM/SC junctions.[4,5]From the band structure point of view, the Andreev retro-reflection occurs where the incident electron and the reflected hole come from the same band (conduction band or valence band). While, specular AR happens when the incident electron and the reflected hole are from conduction and valence bands,respectively.[6–8]Very recently,Zhang and co-workers[9]reported a theoretical investigation of the spin-dependent AR process in a graphenebased superconducting junction. They provided a method to experimentally distinguish the specular AR from the conventional retro-reflection by measuring the tunneling conductance and shot noise in graphene-based ferromagnet/superconductor(FM/SC)junctions.
On the other hand, the transport properties in topological insulator (TI)-based superconducting junctions have also attracted great interests due to the peculiar band structures of TI.[10–20]For example,the tunneling conductance in TI-based FM/SC junctions is studied in order to investigate the effect of both the magneto and Fermi energy mismatch between FM and SC.[16]The interplay between unconventional SC and ferromagnetism in TI-based superconducting junctions is studied in Refs.[18,19]. Recently,Majidi and Asgari[21]investigated precisely the AR process by analyzing the quasiparticles transport through TI-based NM/SC junctions. Their results theoretically revealed the possibility of generating specular AR in the presence of a gate electric field. Complete contrast to the inter-band type in graphene,the coupling between the top and bottom surface of an ultrathin TI can lead to the intra-band specular AR. Later, Islamet al.[22]studied the crossed AR in a TI-based NM/SC/NM junction in the presence of a gate electric field. How to experimentally distinguish the specular AR from the conventional retro-reflection in TI-based superconducting junctions is a natural question. This is one of the motives of our work.
In this paper, we investigate theoretically the spindependent AR by analyzing the electronic transport in a TI-based FM/SC junction. The tunneling conductance and the shot noise are calculated by the Dirac–Bogoliubov–de Gennes (DBdG) equation and Blonder–Tinkham–Klapwijk(BTK) theory. It is found that both the specular AR and the conventional retro-reflection are strongly affected by the ferromagnetic exchange energy and the applied electric field. With the change of the exchange interaction and electric field,there will be a transition from one reflection to another.
2. Theoretical model
Our model is a three-dimensional TI-based FM/SC junction where carriers are confined in thexy-plane. The applied magnetization along thezdirection is in the region forx ≤0 and the SC lies in the region forx>0. The magnetization can give rise to the magnetic energy gap∼2min the density of states of the carriers. An external potentialUof a gate is placed over the superconducting region. Therefore,the Fermi energy in SC equalsEF+UwithEFthe Fermi energy in FM.
The considered system satisfies the following DBdG equation:[23]


The coefficients of normal reflectionre, Andreev reflectionrA, transmission as electron-like quasiparticlete, and transmission as hole-like quasiparticlethin Eq.(2)can be obtained by using the condition for continuity of wave functions at boundary. That isψS|x=0=ψF|x=0.
Based on the BTK theory[24]at zero temperature,the differential conductance of the considered system is written as[16]

3. Results and discussion
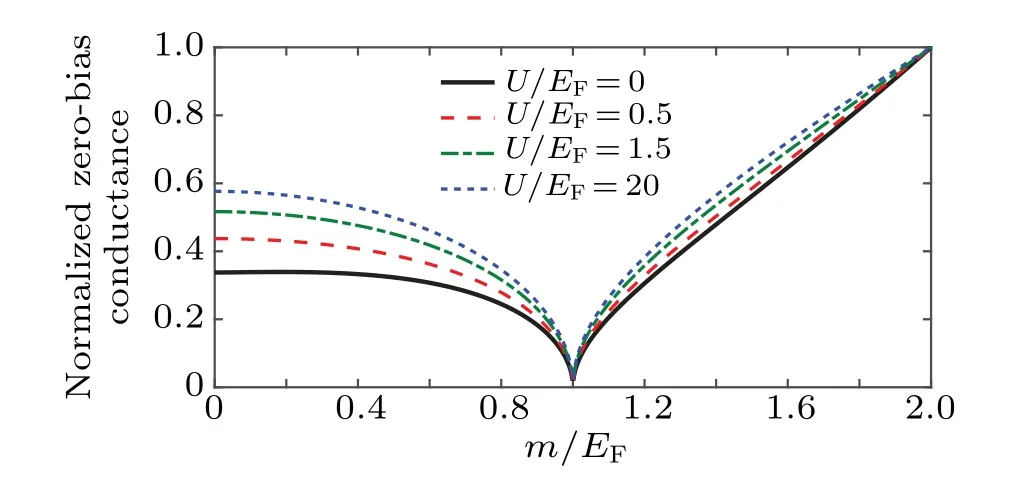
We first study the effect of the magnetic gapmon the spin-dependent AR process in TI-based FM/SC junctions.The tunneling conductance as a function of bias voltage for differentmwithU=10EFis given in Fig.1. It can be seen that,in the case ofm/EF<1,the subgap conductance increases with increasing bias voltage. Whenm=0 a conductance minimum due to the Fermi-level mismatch between FM and SC induced by the gate electric field appears at zero energy and a peak caused by the Andreev resonance occurs at the point where the applied bias voltage is equal to the amplitude of the superconducting gap,i.e.,eV=∆0.[16]As increasingm,the amplitude of the conductance in the whole energy range decreases.Whenm/EF=1, the tunneling conductance vanishes. In the case ofm/EF>1,the tunneling conductance only exists in the subgap energy range and the subgap conductance increases withmincreasing. These behaviors may be physically explained as follows. In the case ofm/EF<1,the electron–hole conversion is predominant retro-reflection correspondingly the tunneling conductance is also mainly determined by Andreev retro-reflection. In contrast, form/EF>1,i.e.,EF Fig. 1. Tunneling conductance as a function of bias voltage for different magnetic gaps with U =10EF. Fig.2. Normalized zero-bias conductance as a function of magnetic gap for different U. The influence of the electrostatic potentialUon the AR process is shown in Fig. 2 where we plot the dependence of the normalized zero-bias conductance on the magnetic gap for differentU. It is found that for all the values ofm, the conductance is enhanced by increasing the gate potential whenUis small. For values ofU ≫EF, in fact according to our calculation whenU/EF≥20,the conductance spectra remain unchanged. This indicates for largeU,the conductance is independent of the gate potential. Even more interesting is that no matter what the value ofUis, with the increase ofm, the zero-bias conductance first is reduced to zero atm/EF=1 and then goes up. These results show that the gate-induced potential difference between the top and bottom surfaces of the TI can enhance the probability of specular AR and the specular electron–hole conversion can happen in a wide experimentally accessible range of the electric field[21]for the proposed TIbased FM/SC structure. The behaviors of the shot noise are given in Figs. 3 and 4. Figure 3 shows the shot noise spectra as a function of bias voltage for different magnetic gap withU=10EF. One finds that the shot noise, especially in subgap energy, is strongly influenced by the exchange interaction. Just like the subgap conductance, withmincreasing the shot noise in sub-gap region also decreases to zero atm=EFand then increases. In order to see this feature more clearly, we plot the normalized shot noise at zero-bias energy for differentEFin Fig.4. It can be seen obviously that the zero-bias shot noise vanishes whenm=EF. It follows that in this case the Fermi surface just locates at the Dirac point (at which conduction and valence bands touch) and all of the conduction channels are closed.Then there no AR process occurs at the FM/SC interface in the in the same band. Therefore, both the zero-bias conductance and the shot noise vanishes. WhenEF>m,from Eq.(4)we can know the numbers of the electron states contributing to the specular electron–hole conversion from two drops to one asEFincreases. Correspondingly, the dominant AR is retro type and the zero-bias conductance is reduced. The values of the differential shot noise and conductance are equal to zero atEF=mcan be used to judge the presence of specular AR as well as to determine the spin-polarization. Fig.3. Shot noise as a function of bias voltage for different magnetic gaps with U =10EF. Fig. 4. Shot noise as a function of magnetic gap for different EF with U =10EF. In this paper, we investigated theoretically the two types of reflections by the tunneling conductance and shot noise in a TI-based FM/SC junction. It is found that both the magnetic gap (m) in FM region and the gate potentialUapplied to the electrode on top of SC can enhance the Andreev retroreflection. The specular Andreev reflection can be suppressed bymbut enhanced byU. There is a transition between the two types of reflections atm=EFwhere the amplitudes of the tunneling conductance and the differential shot noise become zero. For the proposed TI-based FM/SC structure the specular electron–hole conversion can happen in a wide experimentally accessible range of the electric field.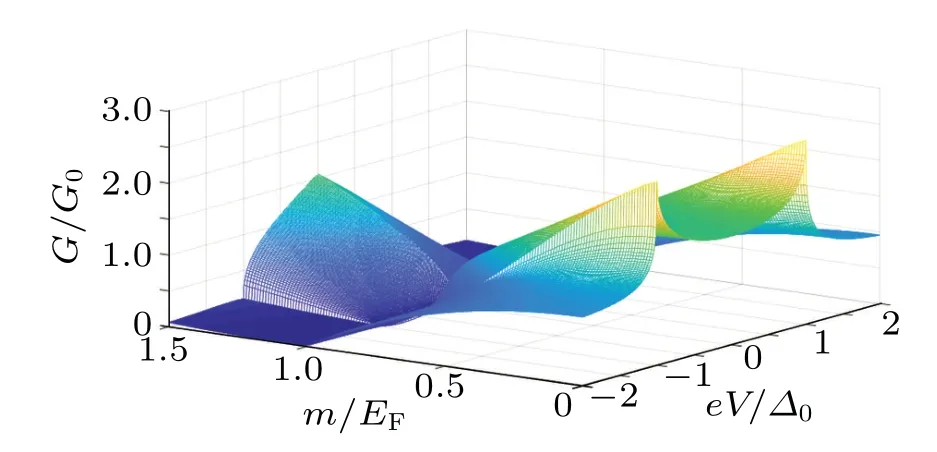


4. Conclusions
- Chinese Physics B的其它文章
- Editorial:Celebrating the 30 Wonderful Year Journey of Chinese Physics B
- Attosecond spectroscopy for filming the ultrafast movies of atoms,molecules and solids
- Advances of phononics in 20122022
- A sport and a pastime: Model design and computation in quantum many-body systems
- Molecular beam epitaxy growth of quantum devices
- Single-molecular methodologies for the physical biology of protein machines

