Advances of phononics in 20122022
Ya-Fei Ding(丁亚飞) Gui-Mei Zhu(朱桂妹) Xiang-Ying Shen(沈翔瀛)Xue Bai(柏雪) and Bao-Wen Li(李保文)
1Department of Materials Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China
2Bourida LLC,Qingdao 264000,China
3Shenzhen Institute of Advanced Electronic Materials,Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen 518055,China
4Department of Physics,Southern University of Science and Technology,Shenzhen 518055,China
5International Quantum Academy,Shenzhen 518048,China
6Paul M Rady Department of Mechanical Engineering and Department of Physics,University of Colorado,Boulder,Colorado 80305-0427,USA
Keywords: phononics,thermal diode,thermal transistor,thermal control devices
1. Introduction
Phonons,quantization of lattice vibration,transport in all solids,carry both energy and information. They are main heat carriers in dielectric and semiconductor materials. Modern information technology is based on semiconductor materials,therefore, phonons have been considered as the main source for information deterioration. Therefore, how to manipulate and control phonons becomes primary importance for microelectronics.
The studies on vibrational energy transfer in various nonlinear lattices in the end of the last century and the early decade of the 21stcentury have been enlightening.[1]These studies have led to a new emerging field–phononics,[2]manipulating and controlling phonons with electronic analogs.
The primary building block for phononics is thermal diode that rectifies phononic heat flow,or a one-way heat flow channel. To perform logic operations and build useful thermal circuitry, additional operational function for phonons is desired. So far, the toolkit for phononics includes thermal diodes,[3–8]thermal transistor,[9–14]thermal logic gates,[15,16]thermal memories,[17,18]thermal regulators,[19,20]thermal switches,etc.[21,22]In addition to the phononic/thermal information processing,these devices are capable of manipulating and controlling heat energy.[22,23]
The last decade, namely, from 2012 to 2022, has witnessed increasing research activities both from scientific and engineering communities, aiming at achieving better performance of these thermal devices.[24,25]Many new models/devices/materials,experiments,and applications have been uncovered, we thus feel a necessity to review these achievements and point out some existing problems and future directions.
In this article, we give a brief review of the progress in this fast-developing field in the past decade, in particular, we focus on fundamental mechanisms, experimental demonstrations,and potential applications of the solid-state thermal control devices,as demonstrated in Fig.1.[26–31]In Section 2,we introduce the latest research in thermal diode. In addition to the classical nonlinear lattices, rectification in quantum systems and topological phononics are also included. We also discuss the related advanced experiments of thermal diode.We turn to the thermal transistors in Section 3. Similarly,both classical and quantum systems are demonstrated. Some practical applications of these thermal devices are discussed in Section 4. Finally,we discuss the challenges and perspectives lying ahead.
2. Thermal diode: theory and experiment
Thermal diodes are the fundamental tools for manipulating and controlling the heat flux. If a positive thermal bias is applied, the device acts as a thermal conductor, while in the opposite case, it shows poor thermal conduction. In general,the thermal rectification effects of the thermal diodes are mainly contributed by the asymmetric interfacial thermal resistance and asymmetric phonon propagation depending on the material structure or properties.[2,32]Many achievements have been made from its infancy. In this section,we focus on the advances in the last decade.
2.1. Theoretical research of thermal diode
2.1.1. Classical systems
The phononic thermal diode was modeled via anharmonic lattice with inherent symmetry breaking.[2]The concept has been put forward by Terraneoet al.[3]in 2002 with three segments of different nonlinear lattices. The underlying physical mechanism relies on the temperature-dependent power spectrum due to nonlinearity. In 2004,Liet al.[4]proposed a twosegment model that has increased the rectification coefficient for several orders of magnitude.From the point of power spectrum, it was reported that the heat energy is exchanged efficiently when the power spectra of the two segments match or overlap. In the absence of spectra overlap,there is no or very little energy exchange between the two segments. This spectral match/mismatch property provides the fundamental mechanism for thermal diodes. Moreover, Liet al.[33]have found that the match/mismatch of spectra also led to an asymmetric interfacial thermal resistance. These works lay the foundation for the series of further works in recent years.

Fig. 1. An overview of phononic devices: (a) a suspended monolayer graphene based thermal diode.[26] (b) Heterogeneous irradiated-pristine polyethylene (PE) nanofiber junction as a nanoscale thermal diode.[27] (c) Schematic diagrams of the macroscopic thermal diode.[28] (d) Crosssectional view of the electrochemical thermal transistor under operation.[13] (e) Schematic drawing of the thermal full adder.[16] (f) Concept of“the thermal doubler”,which consists of thermal diodes and thermal masses,converts a sinusoidal TA into a quasi-constant temperature differential(T1 −T2)across the heat engine. T1 remains close to maximum-TA and T2 close to minimum-TA at all times.[29] (g)Quantum system made up of 3 two-level systems(TLS)coupled with each other and connected to a thermal bath.[14] (h)A schematic diagram of the topological phononics diode based on a three-terminal system. The edge states flow from the terminal A to B without any scattering,while the back flow from terminal B to A is exactly zero,the input from B all flows out through C.[30] (i)Configuration of the thermal transistor.[31] (j)Two-segment thermal diode composed of two different Frenkel–Kontorova chains.[2]
In order to further improve the performance and understand the mechanism of thermal diodes, many efforts have been made from various perspectives. However, one of the most severe shortcomings of these devices, which becomes urgent to be solved, is the rapid decrease of rectification factor as the system size increases.[34]It is demonstrated that long-range interactions can strongly enhance the rectification in mass graded systems and the rectification does not decrease when the system size increases(see Figs.2(a)and 2(b)[5]).It is quite clear that the size-dependence rectification factor for the long-range interactions case is quite different from that in the nearest neighbor case where the decay of the rectification factor with the system size is evident. The mechanism can be described as follows:with long-range interactions,new heat flow channels appear. In addition, the new channels connect with distant particles with different masses, favor the asymmetric heat flow in a graded system. Moreover, new particles are introduced with the increasing of the system size, which can create new channels to avoid the decay of rectification as the system size increases as usual.[5]It does,however,bring a new puzzle. The intriguing problem is whether the efficient rectification can be reached with short range interactions in this system. After that, the next-nearest-neighbor (NNN) interaction is added in the anharmonic oscillator lattice. It is remarkable that the rectification efficiency increases quite rapidly with the system size until it reaches a certain value for large sizes in Fig.2(c).[34]
In addition to the effects of interactions range in the lattice, the section between the two segments also plays an important part in thermal diode.Chenet al.[35]shows an efficient thermal diode with two diffusive leads separated by a ballistic spacer(see Fig.2(d)),where the interaction between the particles is harmonic. The size dependence of the rectification factor vanishes for the case with a ballistic spacer. In Fig. 2(e),we can clearly see that the rectification factor does not decay with the system size. Afterwards, a localized thermal diode model(see Fig.2(f)),which uses a one-dimensional Frenkel–Kontorova (FK) model with a local finite depth defect with asymmetric coupling,achieves a high rectification factor. The defect shown in Fig.2(g),which is locally decoupled from the phonon bands, leads to effective phonon Rayleigh scattering and low thermal conductivity. However, the diode oscillator escapes the defect above a critical local temperature and leads to high thermal conductivity. The key thermal conduction effects are confined to the defect,which means there is no need for a bulk temperature-dependent thermal conductivity,or the need for two different materials.[36]

Fig. 2. Thermal diode toy models in one dimension. (a) The schematic plot of a graded mass (or graded structured) model with the long-range interactions. (b)Dependence of rectification factor(fr)on the system size N(LRI,the case of long-range interactions;NN,the system with nearestneighbor interaction).[5](c)Thermal rectification r as a function of the system size N for a mass-graded lattice with Mmax=10 and various γ values(The tunable parameter γ specifies the relative strength of next-nearest-neighbor coupling compared to the nearest-neighbor one).[34](d)Schematic drawing of the model with two diffusive leads separated by a ballistic channel.[35] (e)Thermal rectification factor versus system size Ntot for chains with or without the ballistic channel.[35](f)Configuration of the localized thermal diode:(i)and(iv)represent identical materials separated by(ii)a material with a temperature-dependent phonon spectrum and (iii) a low thermal conductivity material.[36] (g) Schematic diagram of the thermal diode from the point of phonon band.[36]
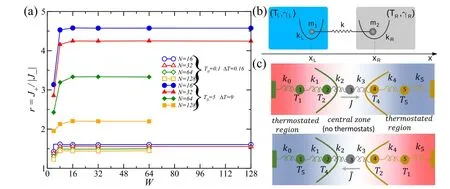
Fig. 3. Thermal rectifier toy models in 3D and others. (a) Thermal rectification r vs. system width W for lateral lengths of N =16 (circles), 32(triangles),64(diamonds),and 128(squares)with Mmax=10,Mmax is the mass of any oscillator in the leftmost.[38](b)Diagram of the model based on two harmonic oscillators(Two masses are coupled to each other through a spring constant k. Each mass is harmonically trapped and connected to a bath characterized by its temperature Ti and its friction coefficient γi).[39] (c)A thermal rectifier based on an N=5-bead harmonic chain. Two beads at the boundaries are considered part of the solids,and they directly exchange energy with Langevin thermostats.[40]
There are many works that demonstrated the possibility of manipulating heat flow by changing the structure or parameters of a one-dimensional anharmonic lattice. Although the dimension extension of the aforementioned coupled FK and Fermi–Pasta–Ulam (FPU) lattice system has been performed in both two[41]and three dimensions,[42]with high rectification efficiencies as in the corresponding 1D case,the studies of 2D and 3D thermal diodes in other systems in two-dimensional or three-dimensional systems have not been as extensive as that in one-dimensional systems.
To further optimize the parameters, Bastidaet al.[38]extended the study to a 3D mass-graded anharmonic lattice of lengthNand widthW. The lattice sitenis expressed as (n1,n2,n3), wheren1=n2=1,...,Wandn3=1,...,N. The relationship between the rectification efficiency and the system widthWfor various lateral system lengthsNand two values of the average temperatureT0is shown (see Fig. 3(a)). It is clear that,for any fixed lateral lengthN,the value of rectification(r)increases as we increaseWbut saturates quickly after a crossover widthWc∼16. It is important to refer that the best rectification values reported occur at an average temperature valueT0=5,where no rectification is obtained in the 1D case.Despite its low rectification power, the system is more robust against a deterioration of thervalue over a wider temperature range than its 1D counterpart, making it suitable for a larger class of possible applications.
Except the research mentioned above, there are still a number of works based on anharmonic segments. A question is whether the rectification effect can emerge in the harmonic systems. Sim´onet al.[39]studied the heat rectification in a minimalistic model composed of two unequal atoms subjected to linear forces and in contact with effective Langevin baths induced by Doppler lasers in 2021. The diagram of the model is shown in Fig.3(b). The proposed model,which consists of two massesm1andm2coupled to each other by a harmonic interaction with spring constantkand natural lengthxe,can be realized with trapped ions subject to Doppler cooling lasers. A thermal rectifier based on anN=5-bead harmonic chain is demonstrated in Fig. 3(c). Two beads at the boundaries are considered part of the solids, and they directly exchange energy with Langevin thermostats. Kalantaret al.[40]proved that perfectly harmonic junctions can rectify heat once the reservoirs(described by Langevin white noise)are placed under temperature gradients,which are asymmetric at the two sides,an effect called“temperature-gradient harmonic oscillator diodes.”
2.1.2. Thermal diode in quantum systems
The successful research in thermal diode has inspired researchers in different fields and communities.The concept has been extended to photonic thermal diode,[43,44]electronic thermal diode where heat is carried by electrons,[45,46]topological phononic diode,[30]quantum-optical model,[6,47]acoustic diode,[48,49]radiation thermal diode,[50–52]and elastic energy diode.[53–55]In this section,we concentrate only on newly developed diodes relevant to phonons in quantum systems.
Topological phononics, that makes use of degrees of freedom like Berry phase and topological order, brings in a new paradigm to phononics. In 2017, Liuet al.[30]derived a Schr¨odinger-like equation of phonons,where topological quantities and time-reverse symmetry (TRS) can be developed for investigating phonons transport. With regard to the Haldane model in quantum Hall effect,[56]they extended it to the novel quantum anomalous Hall-like phonon states.The one-way edge states of quantum anomalous Hall (QAH)like states are ideal channels to realize dissipationless phonon wave guides due to the absence of backscattering channels,and it can be utilized to realize ideal phonon diodes in a multiterminal system. As shown in Fig. 4(a), the edge states flow from the terminal A to B without any scattering,and the back flow from terminal B to A is exactly zero. The one-way edge states give perfect diode effect between any two of the terminals in the three-terminal transport system. It provides unprecedentedly new ways to control phonons.[30,57]
Thermal rectification in quantum systems also draws attention.[58–62]Based on the solution of a master equation for the density matrix,Mirandaet al.[63]demonstrated that two interacting spin-like systems,which are characterized by different excitation frequencies and coupled to a thermal bath, can be used as a quantum thermal diode (see Fig. 4(b)). Another quantum thermal diode,which is composed of two qubits coupled via anisotropic exchange interaction (Fig. 4(c)), undergoes rectification even if the baths produce equal dissipation rates of the qubits. The heat flow rectification process can be explained in Fig.4(d). Interestingly,the model might be realized in various platforms.[47]
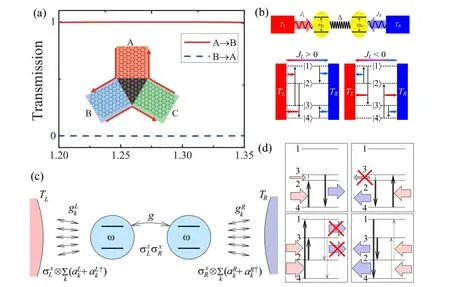
Fig. 4. Thermal diodes in quantum system. (a) Phonon transmission functions for transport from terminal A to terminal B (red solid line) and from B to A (blue dashed line) in three-terminal transport systems.[30] (b) Scheme of a quantum thermal diode made up of two interacting spin like systems connected to thermal baths at temperatures TL and TR.[63] (c)Schematic diagram of the quantum thermal diode based on two resonant qubits(ωR =ωL =ω)coupled via anisotropic spin–spin interaction σzLσxR, the coupling strength between the qubits being g.[47] (d)Examples of processes that rectify heat current with resonant qubits.[47]
2.2. Experiments of thermal diodes
In the above section, we have summarized various theoretical setups and mechanisms. In this section, we discuss how to put these concepts into reality with physically realistic systems.
Since the first experimental work of solid-state thermal rectifier in asymmetric nanotubes in 2006,[64]wherein the rectification varied from 2%to 7%,significant progress has been achieved in variant systems,in particular,the rectification has been increased. Finite size and the discrete phonon spectrum result in a distinct dependence of the thermal quantities on the specific geometrical configuration, mass distribution, and ambient temperature, therefore, the nanosized materials are promising candidates for phononic devices.[2,65]However,because of the difficulty in constructing a nonlinear structure in one-dimensional or two-dimensional nanomaterials, it is still technically challenging to realize rectification at the nanoscale.On the other hand, what makes people excited is the emergence of thermal rectification in a macroscopic system. In this section, we will introduce the experimental progress of the conductive thermal diode from two aspects: microscopic and macroscopic.
2.2.1. Microscopic system
From the perspective of material engineering and miniaturization,the combination of different materials[66]and modification of the shape or size[26,67]of the device are the two general pathways to realize rectification. In 2017,Yeet al.[66]demonstrated that interface-induced thermal rectification can be realized by molecular dynamics (MD) simulations (see Fig. 5(a)) and sophisticated experiments (Fig. 5(b)). The thermal diode consists of polyamide (PA) and silicon (Si)nanowires (NWs) in contact with each other. It was shown that the thermal rectification fluctuated between 2.7% to 3.5% as the temperature varies. After that, using a heterogeneous“irradiated-pristine”polyethylene nanofiber junction (Fig. 5(c)), Shresthaet al.[27]demonstrated an unusual dual-mode solid state thermal rectification effect. It is worth mentioning that heat flow could be rectified in both directions by changing the working temperature, and the maximum rectification factor of 50%was achieved. By the similar way of electron beam (E-beam) irradiation, Liuet al.[68]experimentally demonstrated thermal conductivity manipulation and thermal rectification inπ-stacked metallophthalocyanine(MPcs)NWs(Fig.5(d)). Beyond that, Wanget al.[26]experimentally demonstrated thermal rectification in various asymmetric monolayer graphene nanostructures. A large thermal rectification factor of 26%was achieved in a defect-engineered monolayer graphene (see Fig. 5(e)) with nanopores on one side. A thermal rectification factor of 10%was achieved in a pristine monolayer graphene with nanoparticles deposited on one side or with a tapered width.Moreover,Aiyitiet al.[67]experimentally demonstrated considerable thermal rectification in the Y-junction carbon nanotube (CNT) bundle with suspended thermal bridge method. The thermal rectification ratio was up to∼8.3%±0.5% with a relatively low temperature difference(∆T=4 K).
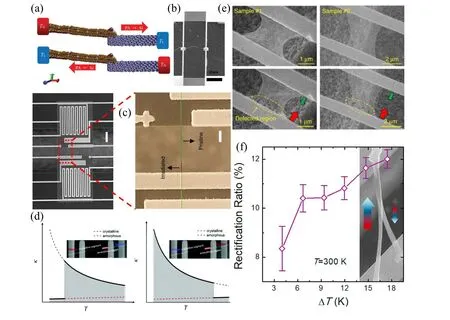
Fig.5. Thermal diode in microscopic scale. (a)Schematic of the MD simulations method for the polyamide(PA)and silicon(Si)nanowires.[66](b)The specimen of the thermal diode(PA and Si nanowires)after focused ion beam(FIB)cutting,scale bar: 20µm.[35] (c)Heterogeneous irradiated-pristine polyethylene(PE)nanofiber junction as a nanoscale thermal diode,scale bar: 10µm.[27] (d)Mechanism of a two-segment thermal rectifier(π-stacked organic nanowires).[68] (e) Scanning electron microscopy images of graphene based thermal diode (suspended monolayer graphene before and after defect engineering).[26] (f)Rectification behavior in the Y-junction CNTs bundle(with the ambient temperature set at T =300 K.The inset is the SEM image of the Y-junction CNT bundle after electron beam induced Pt/C deposition. The scale bar is 1 mm).[67]
2.2.2. Macroscopic thermal rectification
Although extensive research has been done in microscopic thermal rectification, the macroscopic control of ubiquitous heat flow remains poorly explored. By establishing temperature-dependent transformation thermotic for treating materials whose conductivity depends on temperature,Huanget al.[28]demonstrated analytical and simulation evidence for switchable thermal cloaking and a macroscopic thermal diode based on the cloaking. The scheme of experimental demonstration and temperature distribution of the macroscopic thermal diode is shown in Fig.6(a). When cold water is filled in the left container (light blue) and hot water in the right container(pale red),the bimetallic strips of shape memory alloy and copper (white) warp up and the device blocks heat from right to left. While the two containers swap their locations, the bimetallic strips (white) flatten and the device conducts heat from left to right. These results provided a fundamental theoretical method for achieving macroscopic heat rectification. Moreover,based on fractal structures with liquid metal/insulator, Liet al.[69]developed a thermal diode with the rectification up to 0.47. The optimal branch morphology and parameters of the diodes are shown in Fig.6(b). What is really meaningful is that different arrangements of two thermal diodes mounted on chambers’square surfaces are capable of producing different interior temperatures in the same ambient conditions. It has great potential in thermal management.Lately,a super-flexible thermal diode based on Kevlar aerogel confined phase change fluid films was constructed,exhibiting excellent flexibility (420 µm in curvature radius) and robustness (≥7.2 MPa in tensile strength). As shown in Fig. 6(c),this thermal diode also demonstrates a robust thermal rectification with maximum thermal rectification of 2, and high reliability which fluctuates between 1.94 and 2.03. It provides a promising strategy for designing more practical thermal diodes and thermal devices.[70]
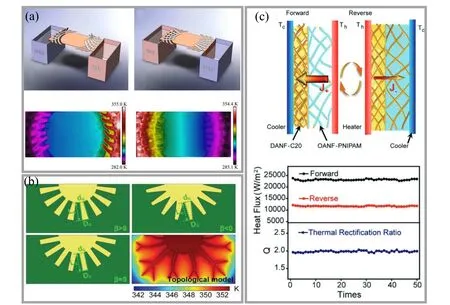
Fig.6. Thermal diode in macroscopic scale. (a)Scheme of experimental demonstration and experimentally measured temperature distribution of the macroscopic thermal diode.[28] (b) Thermal diodes based on fractal structures of liquid metal/insulator with different branch morphologies,including tapered shape (β >0), inverted tapered shape (β <0), rectangular shape (β =0), and topological branch.[69] (c) Mechanism, cyclic stability of the forward and reverse heat fluxes,and thermal rectification ratio of the flexible thermal diode.[70]
3. Thermal transistor
Thermal diode presents the first step toward phononics.In order to realize logic operations and thermal management,more control mechanisms for heat flow are desired. Thermal transistor, the thermal analogs of an electronic transistor, which allows for an accurate control of heat flow similar to the control of charge flow in a field-effect transistor, consists of three terminals: the drain(D),the source(S),and the gate(G).[71]When a constant temperature bias is applied between the drain and the source, the thermal current flowing between the source and the drain can be fine-tuned by the temperature that is applied to the gate.Liet al.[9]proposed the first model of a thermal transistor in 2006. The research field has been also extended to quantum systems,[11,14]radiation[72,73]and acoustic[74]in recent years. Classical systems based on conduction and quantum systems are the main areas of concern in this section.
3.1. Theory
In order to get the amplification of current change in a thermal transistor, negative differential thermal resistance(NDTR) is needed. The current amplification factorα=∂JD/∂JO(the drain currentJD, the gate currentJO) can be recast in terms of the differential thermal resistanceα=|rS/(rS+rD)|(the differential thermal resistances of the drain segment and source segment arerDandrS,respectively). It is easily seen that ifrSandrDare both positive thenα<1,which means that such a thermal transistor never works. For a transistor to work, it is necessary to have the amplification factor larger than one,α>1, which implies a negative differential thermal resistance.[2]
NDTR occurs at the interface between the source and drain, over a wide regime of parameters, when the gate temperature rises,the heat currents of the source and the drain may increase simultaneously.[2]The phenomenon of NDTR can be understood from the mismatch between the phonon bands of the two interface particles as shown in Fig. 7(a), where we plot the power spectra of the two interface particles at different temperaturesTLfor a fixedTR. As can be seen,the overlap of the power spectra increases asTLincreases. Therefore, by increasingTLwe have two competing effects:the thermal gradient decreases and the band overlap increases. The behavior of the heat current depends on which of these two effects prevails,that resulting in the NDTR.[9]
Much effort has been put to realize/improve the NDTR,[75,76]and extend to two-dimension,[77]while the role of the gate segment has been neglected. In 2020,Ruanet al.[31]studied systematically the role of the gate segment and revealed the crucial importance of its thermal resistance. The configuration of the thermal transistor is shown in Fig.7(b),the ends of the segments S and D are always attached to heat baths with temperaturesTSandTD, respectively. The positive directions of the heat currents flow through the particle O are illustrated by the arrows.When the heat resistance of the segment G(RG)is lower than a critical value,the transistor can be set exactly to on and off states by setting the control temperatureTGtoTonandToff. And the thermal transistor can be set to any stable steady state whenRGis lower than an even lower critical value.This study helps to design thermal devices that complete desired functions. Remarkably,Behniaet al.[78]introduced a highly efficient thermal transistor based on the simple configuration of DNA molecule. It was shown that the DNA thermal transistor can act as a switch,modulator and amplifier. The ratio of heat current in the on-state to the off-state is attained as high as 700 (Fig. 7(c)). The physical mechanism of the system can be explained as follows,driven by the changing of the system’s conduction phase between ballistic and diffusive regimes, it shows switching performance. Exactly, in the ballistic regime, the decrease in the specific heat will induce an increase in the mean free path of phonons so it implies an increase in the thermal flux despite decreasing temperature gradient.
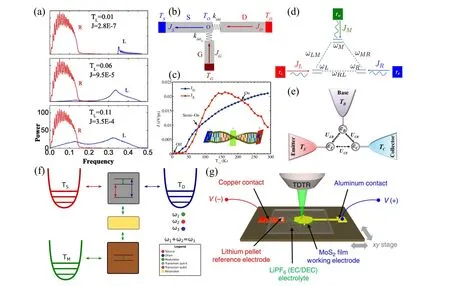
Fig.7. Principle and models of thermal transistor. (a)The power spectra of the particles at the right(R)side and the left(L)side of the interface for different temperatures TL with fixed TR=0.2.[9](b)Configuration of the thermal transistor.[31](c)A schematic representation and switching operation of a DNA thermal transistor.[77] (d)Quantum system made up of 3 two-level systems(TLS)coupled with each other and connected to a thermal bath.[14](e) The schematic diagram of a quantum-dot thermal transistor. Three Coulomb-coupled quantum dots are connected to the respective electronic reservoirs. The Coulomb interaction UCE between the collector and the emitter is adjustable.[11] (f) Conceptual model of the thermal transistor.[79](g)Experimental measurement of the electrochemical thermal transistor.[13]
On the other hand,the study of thermal transistor has been extended to quantum regime. Coupled with a thermal reservoir, Joulainet al.[14]demonstrated a quantum thermal transistor in 3 two-level systems (TLS), which are equivalent to the three entries of a bipolar electronic transistor. It is demonstrated in Fig. 7(d) that one TLS which plays a similar role as the base in a bipolar transistor is coupled to other two TLS that can be treated as the emitter and the collector. An amplified variation at the emitter and the collector is generated when the base varies in a certain temperature regime. This regime is typically such that temperature corresponds to an energy one order of magnitude smaller than the coupling energy between the TLS.In principle, the proposed quantum transistor could be used to develop devices such as a thermal modulator and a thermal amplifier in nano systems. Afterwards, based on the Coulomb-coupled quantum dots, Zhanget al.[11]constructed quantum-dot thermal transistors. It is demonstrated that a small change in the heat flow of the base can induce a large heat flow change in the collector and emitter. By adjusting the Coulomb interaction between the collector and the emitter or by decreasing the tunneling rate at the base,the amplification factor can be optimized. The schematic diagram of a quantum dot thermal transistor can be seen in Fig. 7(e). It is worth mentioning that three quantum dots are capacitively coupled to each other and interact only through the long-range Coulomb force,so that there is no electron transport between the quantum dots.When a constant temperature bias is applied to the emitter and the collector,the heat flow between the emitter and the collector is generated by electrons tunneling into and out of the dots,then exchanging energy through Coulomb interaction can be fine-tuned by the temperature applied to the base. These results will stimulate interest for the quantum-dot thermal transistor. On the basis of this work,Majlandet al.[79]proposed a concrete realization of a superconducting circuit that can work as a thermal transistor in 2020. Using a circuit quantum electrodynamics Jaynes–Cummings model, the proposed three-terminal device allows heat transfer from source to drain, depending on the temperature of a bath coupled at the gate modulator,shows that it provides similar properties to a conventional semiconductor transistor(see Fig.7(f)).
3.2. Experiment
Despite the scientific and technological significance of thermal transistors,little progress has been made in the experiment. Until 2018,based on reversible electrochemical lithium intercalation in MoS2thin films,Soodet al.[13]demonstrated a switchable electrochemical thermal transistor with an order of magnitude thermal on/off ratio. By reversible intercalation of Li ions, with the on-state corresponding to the pristine MoS2and the off-state corresponding to the Li-intercalated MoS2,real-time modulation of thermal conductance is achievedin situtime-domain thermoreflectance(TDTR).The experimental measurement of the thermal transistor can be seen in Fig. 7(g). Based on the experiment result and simulations(ab initioand non-equilibrium molecular dynamics),it is suggested that a combination of multiple factors is likely to lead to such a significant modulation of thermal conductance,including enhanced phonon scattering from Li rattler modes,phonon softening due to lithiation-inducedc-axis strain,stacking disorder(2H-1T phase mixtures),and mesoscopic disorder. This study lays the foundation for electrochemically-driven thermal transistors.So far,the development of solid-state thermal transistors mainly focuses on electrochemical systems.
4. Potential applications
Except the research in theories and experiments,thermal control devices have tremendous applicable potential. In this section,we will discuss the possible applications of the device mentioned above in thermal management and thermal circuits.
4.1. Thermal management
There are rapid growing needs in thermal management,especially in electronic devices,electric vehicles,communications system, data center and even future quantum technology.[81–84]Phononic devices are good candidates in solving complicated thermal management problems. As shown in Fig. 8(a), a fractal structures thermal diode is designed to mount on the chamber’s different surfaces to provide interior temperatures ranging from 16.06°C to 52.34°C in the same ambient conditions. These controlled temperature chambers will meet the needs for different thermal thresholds in thermal management. On the other hand,based on the caloric effect,the temperature of caloric materials varies with the change of external parameters,such as magnetic field,[85]electric field,[86]stress[87]and so on. It is a promising alternative to refrigeration technology.A caloric refrigeration usually consists of a caloric material,heat source,heat sink,and heat transfer medium. The application of thermal diode in a caloric system means higher operating frequencies, which would increase the cooling power density and the compactness of the device.The mechanism is shown in Fig.8(b),the caloric material can be embodied within two thermal diodes,of which one part serves as the thermal connection between the caloric material and the heat source,and the other as the thermal connection between the caloric material and the heat sink. When the caloric material is heated due to the caloric effect,the thermal diode allows the heat to flow only from the caloric material toward the heat sink and simultaneously prevents any heat flux from the caloric material to the heat source. In contrast,when the caloric material is cooled with the caloric effect,the thermal diode allows the heat to flow only from the heat source to the caloric material and simultaneously prevents any heat flux from the heat sink to the caloric material.[80]

Fig.8. Applications of phononic device. (a)Performance of thermal diodes on temperature chambers with different arrangements.[69](b)Schematics of implementing thermal diodes in a caloric device.[80] (c)Schematic drawing of the thermal full adder.[16]
4.2. Thermal logic gates
In electric circuits,two Boolean states 0 and 1 can be encoded by two different values of an electric potential. The analogy between Boolean operations and electronic digital circuits, which is highlighted by Shannon in 1938, paved the way for modern computation based on electronic devices.[88]However, with the continuous increase of power density, the chips began to get too hot.[89]Manipulating phonons like electrons may be an alternative scheme for information technology. Based on nonlinear lattices, Wang and Li built up the thermal logic calculation from the thermal transistor model(thermal AND/OR gate) in 2007.[15]Lately, Hamedet al.[18]simulated a thermal calculator based on thermal logic gates that can perform similar operations as their electronic counterparts. In Fig. 8(c), it is shown the schematic drawing of the designed thermal full adder, which consists of AND,OR and NOT gates,is the key to most digital circuits that perform addition or subtraction.And then,a thermal calculator which can perform the addition of two decimal numbers was developed.They demonstrated the ability of information processing based on thermal diode and transistor.
5. Summary and perspectives
We have made a brief but rather complete review of the progress of phononics in the past decade. First of all, the research field has been largely extended from classical systems to quantum regimes and topological phononics. On the other hand, more and more materials have been explored for the phononic devices such as graphene, silicon, germanium,phase-change material,liquid crystal,polymeric fibers,liquid metal and so on. All of these studies not only provide the physical mechanisms but also provide material database for phononic devices,which is a significant step toward the practical applications.Like other emerging fields,the more studies are done,the more opportunities and more challenges emerge.Here we point out some interesting perspectives that deserve further investigations.
Figure of merits Thermal rectification is widely utilized to quantify the performance of thermal diodes. However, the definition of thermal rectification ratio (r) varies in different papers. For example,[4,5,36,45,69,90,91]


whereκfandκrare the thermal conductance/conductivity in the forward and reverse directions,respectively. Although the performance of the thermal diode gets better when thermal rectification ratioris higher. The different definitions still cause problems for the performance evaluation of different studies. There is an urgent need for a unified parameter. In addition, the rectification of thermal diodes depends on both the temperature difference and the absolute magnitude of the temperature. But all definition so far has not taken this into account. We may need a more complete parameter like the thermoelectric figure of merit(ZT)for thermoelectric materials.
Fast, reliable, powerful and robust measuring techniqueThe development of thermal conduction measurement technologies has laid the groundwork for experimental progress and applications of phononics devices. At present,experimental tools, which are used to measure thermal conduction and interfacial thermal resistance on the micro-nano scale, fall into two categories, i.e., the steady-state measurement (including the thermal bridge method[92]and the electron-beam self-heating method[93,94]) and the transient measurement(including the differential 3ωmethod[95]and the pump-probe thermoreflectance technique[96]).Compared with the electronics and optics,the available experimental tools for detecting heat flow are still quite limited. There is an urgent need for more advanced measuring techniques for heat transfer.[97]
From greatest to least,and in reverseWith the rapid development of microelectronics and related industries,the feature size of transistors keeps shrinking and the chip integration and packaging density continue to grow. We also expect the feature size of the single phononic device to decrease continuously. At the same time, they have the capability to be integrated into computer chips.
Bear in mind the practical applicationsThe ultimate goal of phononics is to manipulate/control heat flow,and eventually makes use of heat energy efficiently and smartly. How far the phononics can go depends very much on how many potential applications can be explored. As the continuous improvement of phononics devices,we believe that more specific applications are coming to the spotlight. Although there is a time-lag between fundamental research and applications, the application scenarios should be taken into account in the theoretical modelling/simulation. We believe that the theoretical study will be able to provide guidelines and offer a firm foundation for experiment and application researches.
Thermodynamics constraintSome thermal rectification and/or so-called negative thermal conductivity materials seem to violate the second law of thermodynamics.[98,99]These studies often employ Brownian ratchet-like designs or carefully engineered extremely anisotropic structures to achieve thermal rectification or reverse the direction of thermal conduction.[90,100,101]A closer look at these systems,people will find that they all follow the second of thermodynamics without any exception. In any case,however,heat transfer must obey the second law of thermodynamics in any circumstance,it is the most basic principle and it can be used to screen out some infeasible designs.
Quantum informationThe continuing trend of miniaturization and integration imposes great challenges of thermal management in electronic devices.[102]As for the field of quantum computing, the qubit lifetime and gate operation fidelity are likely to reduce with additional decoherence source.Hence, thermal management of quantum systems becomes more daunting.[82]Phononic devices,with the function of heat flow controlling,are expected to play a more and more important part in quantum technology.
Moreover, as an interdisciplinary subject, phononics needs interactions among researchers from different fields such as physics,material science and engineering,thermal science and engineering. We hope this brief review will be able to bring attention and interactions from researchers in different backgrounds.Acknowledgments
XB is supported by the National Natural Science Foundation of China (Grant No. 62004211) and Shenzhen Science and Technology Program (Grant No.RCBS20200714114858221).
- Chinese Physics B的其它文章
- Editorial:Celebrating the 30 Wonderful Year Journey of Chinese Physics B
- Attosecond spectroscopy for filming the ultrafast movies of atoms,molecules and solids
- A sport and a pastime: Model design and computation in quantum many-body systems
- Molecular beam epitaxy growth of quantum devices
- Single-molecular methodologies for the physical biology of protein machines
- Research progress of Pt and Pt-based cathode electrocatalysts for proton-exchange membrane fuel cells

