对角切片谱提升的形态学滤波方法及其在万向轴故障识别中的应用

李奕璠， 林建辉， 刘伟渭

(1. 西南交通大学 机械工程学院，成都 610031； 2. 西南交通大学 牵引动力国家重点实验室，成都 610031)

对角切片谱提升的形态学滤波方法及其在万向轴故障识别中的应用

李奕璠1， 林建辉2， 刘伟渭1

(1. 西南交通大学 机械工程学院，成都 610031； 2. 西南交通大学 牵引动力国家重点实验室，成都 610031)

针对多尺度形态学滤波器将所有尺度的滤波结果进行算术平均这一问题，提出利用三阶累积量对角切片谱对其进行改进，用于对高速列车万向轴不平衡故障进行检测与识别。该方法首先对安装在齿轮箱的振动传感器采集到的信号进行多尺度形态学滤波，得到不同尺度下的滤波结果，再计算滤波后信号的三阶累积量及其对角切片谱，最后依据对角切片谱的特征频率系数，选取出最能凸显故障特征的切片谱，从而避免了多尺度滤波器滤波结果的算术平均问题。在万向轴不平衡试验台进行了试验，结果表明，该方法能有效地识别出万向轴不平衡引起的基频和倍频故障特征，与传统的多尺度形态滤波相比，此方法更能彰显故障特征。

高速列车；万向轴；多尺度形态滤波；对角切片谱

万向轴是CRH5型列车传动系统的重要组成部件，其两端通过十字万向节分别与牵引电机和齿轮箱相连[1]。由于万向轴为细长杆状结构，其弯曲和扭转刚度都较小。而传动时，万向轴既要传递牵引力矩，又要适应各种运动关系[2]，在此过程中引起的附加力矩容易导致扭转振动[3]。此外，列车长期运行也会使得万向节轴的磨损间隙增大，导致万向轴偏心。上述因素均可能使万向轴产生不平衡，从而加剧传动系统的振动，加速传动系统万向节和轴承的破坏，危及行车安全。因此，对万向轴工作状态进行监测与识别很有必要。

目前，对万向轴状态进行监测和识别的研究并不多见。文献[4]使用第二代小波变化结合奇异值分解的方法对此问题进行了研究，但基于小波分解的方法始终存在基小波与相应参数选取主观性的问题。文献[5]使用经验模态分解，根据特征模态分量的能量大小识别是否存在万向轴不平衡，但其正常样本与故障样本之间的差异并不显著。为此，本文使用基于数学形态学滤波的方法对万向轴不平衡进行研究。相较于文献[4-5]，形态滤波分析方法不需要人为设定参数[6]，结果具有更好的复现性，同时其计算过程只包含加、减和布尔运算，计算速度更快，实时性更好。

但是，传统的多尺度形态滤波器的输出是将每个尺度的滤波结果进行算术平均，这种做法并不合理，因为那些远离理论中心尺度的滤波结果往往被噪声污染，难以有效反映故障特征[7]。针对此问题，本文提出一种利用三阶累积量对角切片谱的方法对多尺度形态滤波器进行改进，以期实现万向轴不平衡的检测。

1 多尺度形态滤波

形态滤波是基于数学形态学变换的非线性滤波方法。它依据待分析信号的局部形态特征，通过一定的形态学变换，将信号与噪声分离。形态学滤波的核心思想是通过结构元素的连续移动，对待分析信号进行匹配，以达到提取信号细节、抑制噪声的目的[8]。

膨胀和腐蚀是形态学变换中两种最基本的运算。设原始信号为f(n) (n=1,2,…,N)，结构元素为g(m) (m=1,2,…,M)，N≥M。f(n)关于g(m)的膨胀和腐蚀分别定义为

(f⊕g)(n)=max[f(n-m)+g(m)]

(1)

(fΘg)(n)=min[f(n+m)-g(m)]

(2)

式中，符号⊕和Θ分别表示膨胀和腐蚀。

f(n)关于g(m)的开运算和闭运算可分别表示为

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f·g)(n)=(f⊕gΘg)(n)

(4)

式中，符号∘ 和·分别表示开、闭运算。

常用的组合形态滤波器由开、闭运算组成

y(n)=[(f∘g·g)(n)+(f·g∘g)(n)]/2

(5)

形态学信号处理的实质是基于试探，即用不同的结构元素去匹配待分析信号[9]。传统的形态学滤波方法中，结构元素一旦选定，其长度和高度在整个滤波过程中不会改变，这种做法对频率结构单一的信号很有效，但是，如果待分析信号的频率成分复杂，单一尺度的形态滤波器难以达到较好的滤波效果。

多尺度形态滤波采用不同尺度的结构元素对信号进行分析。设λ(λ=1,2,…,k)为多尺度滤波器的尺度，g(m)为单位结构元素，多尺度滤波器的结构元素可表示为

(6)

经过多尺度膨胀、腐蚀、开、闭运算后，得到的多尺度组合形态滤波器在尺度为λ的滤波结果为yλ(n)=[(f·λg∘λg)(n)+(f∘λg·λg)(n)]/2

(7)

多尺度滤波器的最终输出为所有尺度滤波结果的算术平均

(8)

文献[10]的研究结果表明，式(8)的处理方式会破坏多尺度滤波器特征提取的效果。因此，本文在第二部分引入三阶累积量对角切片谱方法对多尺度滤波结果进行提升。

2 累积量对角切片谱

长期以来，一阶和二阶统计量被广泛用于振动信号处理，如均值、方差、自相关函数和功率谱等，但这些方法并不能准确描述非线性和非高斯信号，这就需要从更高的阶次上来反映信号特征。目前使用最为广泛的高阶统计量是三阶累计量，三阶累计量的傅里叶变换被称为双谱。由于双谱是一个二维矩阵，计算量较大，难以实现较大数据量的实时计算[11]，而如果使用较少的数据量计算双谱又会增加估计偏差。所以，在实际应用中，常采用三阶累积量的某种一维切片来提取信号的特征，本文使用对角切片。

假设x(t) (t=0,1,2,3, …)为零均值实平稳离散随机过程，其三阶累积量定义为

C3x(τ1,τ2)=E[x(t)x(t+τ1)x(t+τ2)]

(9)

式中：E[·]是求数学期望操作;τ1和τ2是时间滞后。三阶累积量对角切片是三阶累积量在(τ1,τ2)平面内一条τ1=τ2=τ的直线，经过对角切片之后，一个二维矩阵转化为了一个数据序列

C3x(τ)=E[x(t)x(t+τ)x(t+τ)]

(10)

三阶累积量对角切片C3x(τ,τ)的离散傅里叶变换称为对角切片谱或1.5维谱

(11)

相较于双谱，对角切片谱计算量更小，但它保留了高阶统计量分析的优点[12]：

(1) 若x(t)是高斯信号，Sx(ω)=0。这表明对角切片谱可以抑制高斯噪声。

(2) 若x(t)是对称分布的信号，Sx(ω)=0。这说明对角切片谱可以抑制对称分布的噪声。

(3) 若x(t)=p(t)+q(t)，p(t)和q(t)相互独立，q(t)为高斯信号，那么Sx(ω)=Sp(ω)。这意味着对角切片谱可以用来分离加性非高斯信号与高斯噪声。机械振动信号往往被视为非高斯信号，通过对角切片谱分析能够将噪声有效分离。

(4) 对角切片谱能够识别二次相位耦合关系、抑制独立频率分量[13]。

在对万向轴振动信号进行采集时，传感器无法直接安装在万向轴上，只能退而求其次，将其安装在临近的齿轮箱上，这就使得采集到的信号结构较为复杂，它不仅包含了万向轴振动信息，还有齿轮箱自身的振动信息，噪声，甚至从其他部件传递来的振动信息，万向轴故障特征往往被掩盖，而性质1～3能有效降噪，提高信噪比，性质4能凸显故障特征，这就是本文使用累积量对角切片谱对形态学滤波器进行改进的原因。

此外，万向轴不平衡故障的本质为机械转子不平衡，与正常转子相比，不平衡转子的故障特征主要变现为在转动频率及其倍频处振动能量的显著变化。由于万向轴的转动频率较低，而齿轮啮合的频率较高，齿轮箱振动特征与万向轴振动特征容易区分。

3 累积量切片谱提升的多尺度形态滤波方法

本文提出一种累积量切片谱提升的多尺度形态滤波方法，具体步骤如下：①对原始信号进行多尺度形态学滤波，得到不同尺度下的滤波结果；②计算每个尺度滤波结果的三阶累积量对角切片；③得到每个三阶累积量对角切片的对角切片谱；④计算每个对角切片谱的特征频率强度系数[14]，特征频率强度系数越大，故障特征越显著；⑤选出最大的特征频率强度系数对应的尺度，只有这个尺度的对角切片谱被用于故障检测。

由于扁平结构元素结构简单，运算速度快，在进行多尺度滤波时，本文均使用扁平结构元素。对角切片谱提升的多尺度形态滤波方法唯一需要事先确定的参数只有一个，就是多尺度滤波器的最大分解尺度。文献[15-16]将最大的尺度设为采样频率与故障特征频率的商，本文采用同样的方法。

需要指出的是，即使在不知道故障特征频率的情况下，本文方法依然可以进行有效分析。因为本文方法可以从多个滤波结果中选取出一个最能反映故障特征的结果，这样就只需要将最大分解尺度设置为一个较大值就可以了。事实上，这个较大值往往不超过采样频率与故障特征频率的商的0.3倍[17]。

4 试验验证

为了验证本文方法的效果，在万向轴不平衡试验台(图1)进行了试验。试验中，万向轴一端与齿轮箱相连，齿轮箱由电机驱动。将万向轴另一端支撑座垫高，确保万向轴在垂向存在倾角，以模拟列车实际运行状态。振动传感器安装在齿轮箱上最靠近万向轴的非旋转部位，采样频率20 kHz。选用同一型号的两根万向轴进行试验，一根是新轴，一根是存在轻微不平衡的轴，在此将其称之为故障轴。为了将齿轮箱中齿轮啮合频率去除，对采集到的信号进行了1 kHz低通滤波。

图1 万向轴试验台Fig.1 The test rig of cardan shaft

4.1 正常轴的分析结果

万向轴的转速为880 r/min，对应的转频为14.7 Hz。图2为正常万向轴振动的时间历程曲线和频谱。从图2(b)的频谱中，无法找到万向轴转频。

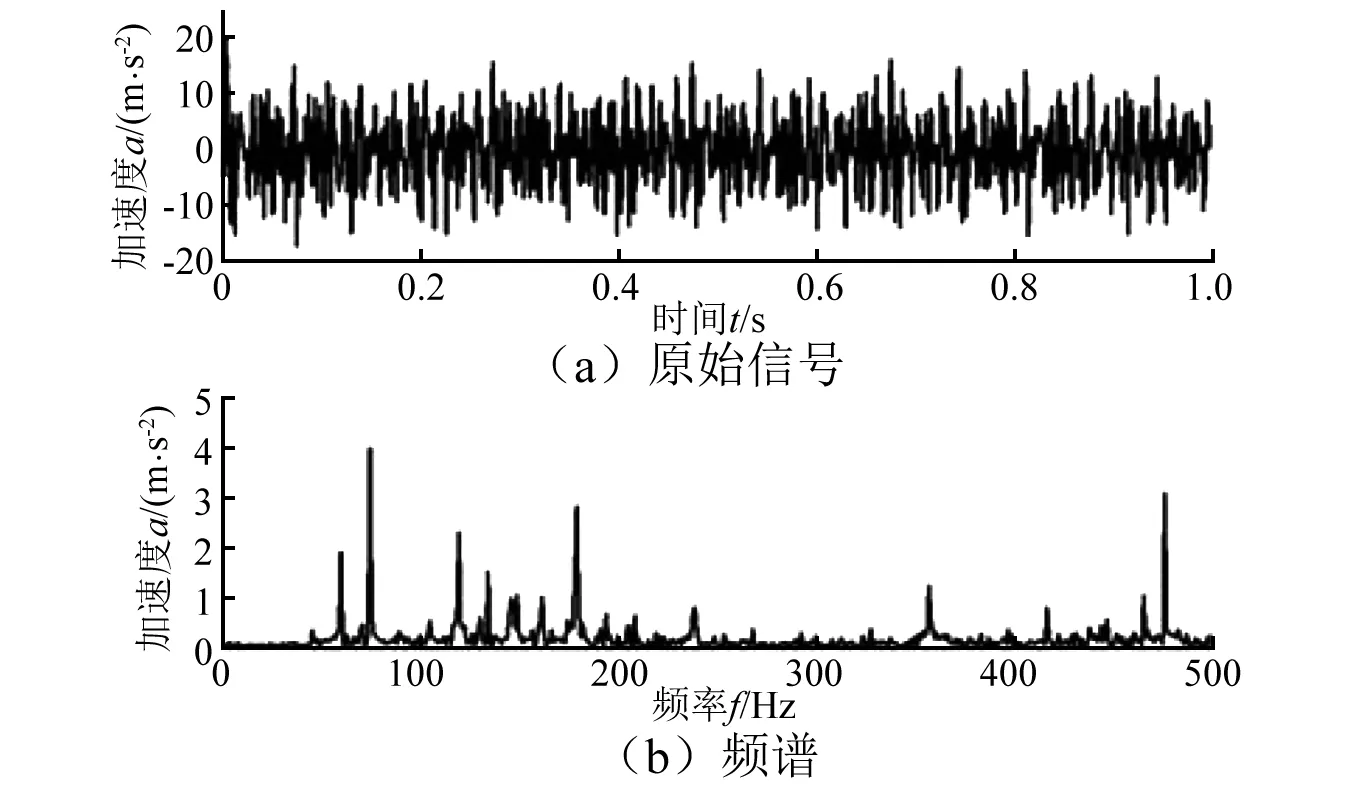
图2 正常轴振动波形及频谱Fig.2 Vibration waveform and frequency spectrum of normal cardan shaft

使用本文方法对正常轴振动信号进行处理。最小的尺度为1，由于进行了低通滤波，最大的尺度设为1 kHz与特征频率的商。尺度的增量为1。因此，共有68个滤波尺度。图3(a)为经多尺度形态滤波后得到的每一个尺度的滤波结果，为了方便观察，只给出了尺度1,7,13,…,61,67等12个结果。对每个尺度的滤波结果求取对角切片谱，同样为了便于观察，图3(b)也只给出了上述12个尺度对应的对角切片谱。每一个对角切片谱的特征频率强度系数如图3(c)所示。可见，尺度5为最优的滤波尺度，因为其特征频率强度系数最大。尺度5的对角切片谱如图3(d)所示，从图3(d)中可以清楚地识别万向轴转频和二倍频。

使用传统的多尺度滤波方法对图2(a)所示的信号进行分析，相应的滤波结果及频谱如图4所示。为了进行公平的比较，与图3的分析使用同样的结构元素和尺度。从图4(b)中可以勉强出识别万向轴的转频，但频谱中最为突出的频率成分与转频及其倍频毫无关系。造成此结果的原因在于，多尺度形态滤波器中，较小的尺度适合于提取冲击特征，较大的尺度适合于抑制噪声，对所有尺度的滤波结果进行加权平均会削弱冲击特征。

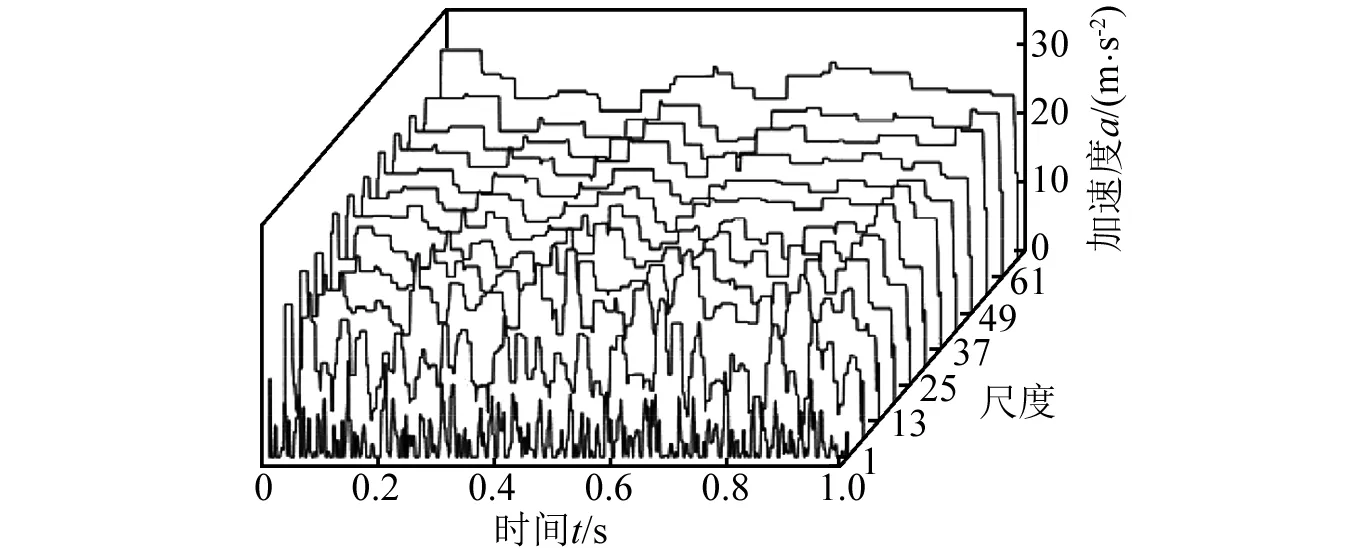
(a) 每个尺度的滤波结果

(b) 每个尺度的1.5维谱

(c) 最优尺度的选择

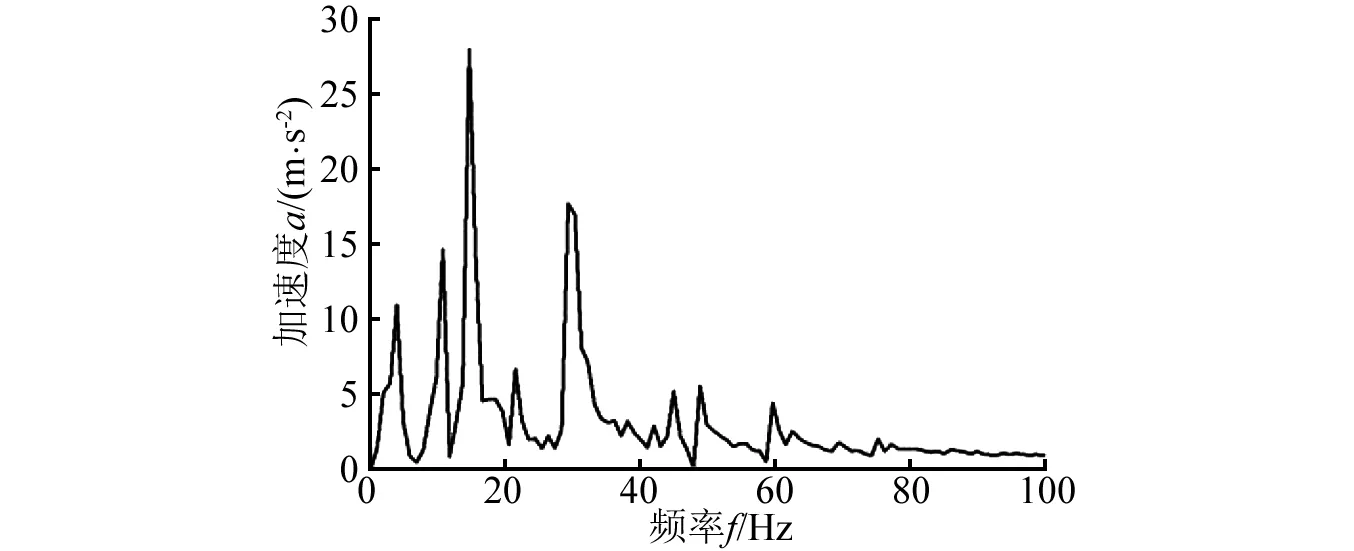
(d) 最优尺度的1.5维谱图3 本文方法对图2(a)信号的分析过程与结果Fig.3 Analysis processes and results for the signal presented in Fig. 2(a) by the proposed method

对比图3(d)与图4(b)可以看到，本文方法在抑制噪声、提取信号特征方面的优越性。从多个尺度的滤波结果中选择一个最优的滤波结果的做法是合理的，同时基于累积量对角切片谱的方法能够进一步抑制噪声，强化故障特征。

4.2 故障轴的分析结果

在同样的试验条件下，对存在轻微不平衡故障的万向轴进行了测试，得到的时域波形及频谱如图5所示。从图5(b)的频谱中很难识别出万向轴的转频和倍频。对比图5与图2，无论在时域还是频域，正常轴与故障轴的差异均不显著。

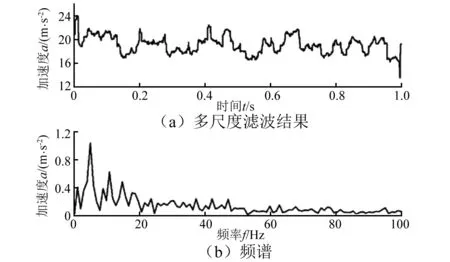
图4 传统的多尺度形态滤波对图2(a)信号的处理结果Fig.4 Analysis results of the signal presented in Fig. 2(a) by conventional multi-scale morphology filtering

图5 故障轴振动波形及频谱Fig.5 Vibration waveform and frequency spectrum of fault cardan shaft

使用本文提出的方法，对图5(a)的信号进行分析。与4.1节采用同样的结构元素，滤波的尺度同样设为68，经多尺度滤波得到的信号见图6(a)，与图3一样，为了便于观察，只画出了其中12个尺度的结果。图6(b)是图6(a)信号的对角切片谱。图6(c)为所有尺度对角切片谱的特征频率强度系数，尺度11的特征频率强度系数最大，因此，确定尺度11为最优尺度。图6(d)为尺度11的滤波结果的对角切片谱，从图6(d)中可以清晰地看到14.7 Hz的转频和二倍频29.4 Hz。在转频(14.7 Hz)的幅值为正常万向轴同一位置(图3(d))幅值的1.45倍，同时在二倍频位置(29.4 Hz)的振幅较图3(d)也有所增加，而这正是典型的转子不平衡故障特征。

此外，从图3(c)和图6(c)可以看到，最优的滤波尺度分别为尺度5和11，均小于最大分析尺度的0.3倍，从而印证了文献[17]的结论。

图7为使用传统的多尺度形态滤波方法对故障轴振动信号进行处理得到的时域波形和频谱。从图7(b)中可以检测到万向轴的转频成分，但此频率被噪声污染，与图6(d)相比，故障特征并不突出，这再次说明了本文方法在故障特征提取方面更为有效。图7(b)在转频(14.7 Hz)的幅值为图4(b)相应位置的1.28倍，这虽然可以用以区分正常轴与故障轴，但差异不如本文方法显著。

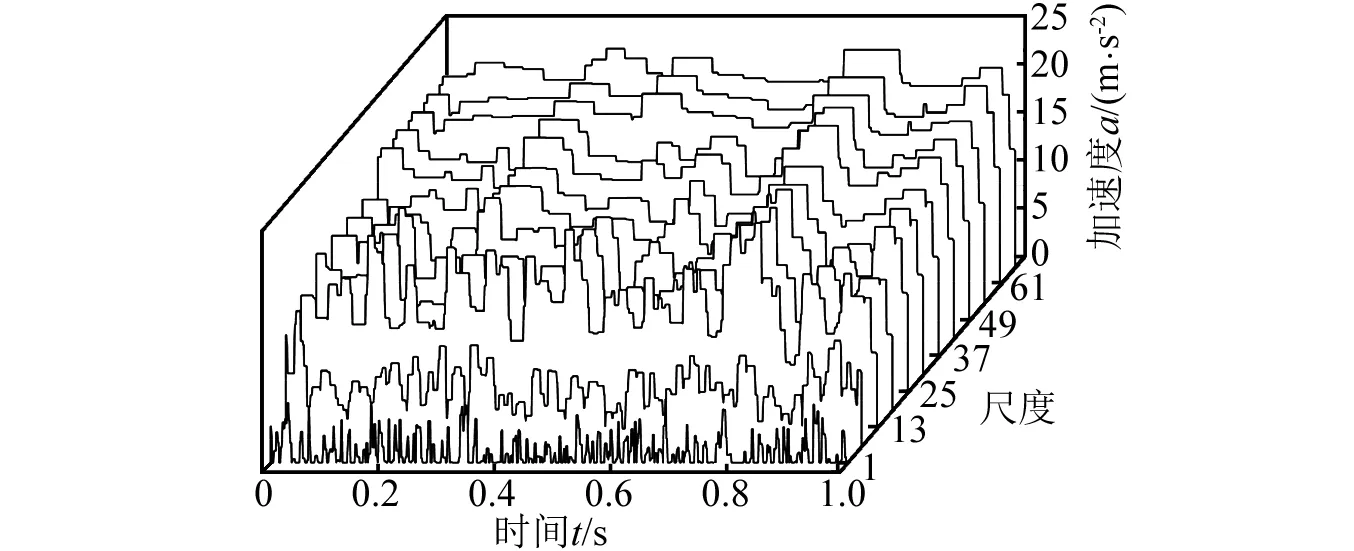
(a) 每个尺度的滤波结果

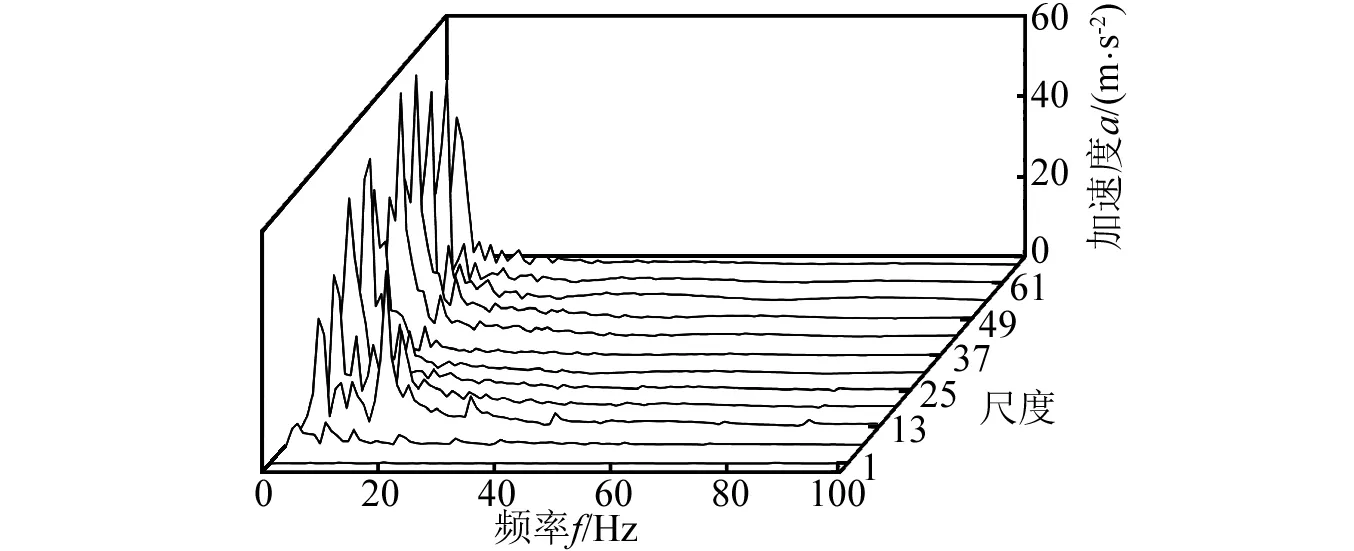
(b) 每个尺度的1.5维谱

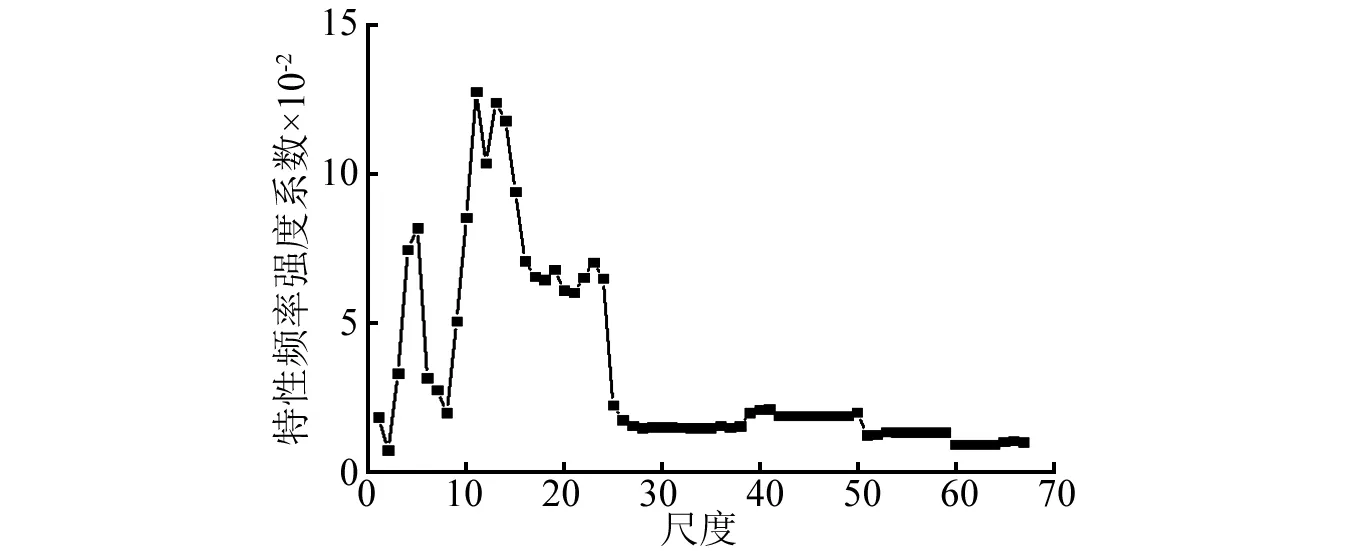
(c) 最优尺度的选择

(d) 最优尺度的1.5维谱图6 本文方法对图5(a)信号的处理过程与结果Fig.6 Analysis processes and results for the signal presented in Fig. 5(a) by the proposed method

图7 传统的多尺度形态滤波对图5(a)信号的分析结果Fig.7 Analysis results of the signal presented in Fig. 5(a) by conventional multi-scale morphology filtering

4.3 讨 论

台架试验中，传感器安装在齿轮箱上，因此，信号中齿轮啮合的信息占有主体地位，信号中反映万向轴振动特征的信息相对较弱。为此，在4.1节和4.2节对试验数据进行处理时，首先进行了1 kHz低通滤波，以去除齿轮啮合频率，提高万向轴故障识别能力。另一方面，如果不进行1 kHz低通滤波，直接用本文的方法对原始信号进行分析，会遇到另外一个问题，那就是多尺度形态滤波的分析尺度。一般来说，多尺度形态滤波的最大分析尺度设为采样频率与故障特征频率的商，本文的采样频率为20 kHz，故障特征频率为14.7 Hz，这就意味着需要使用1 360个尺度对原始信号进行分析。而多尺度形态滤波的原理决定了尺度越大，所需要的计算时间越久，文献[18]研究发现如果尺度1的分析时间为T，那么，尺度10的分析时间约为10T，尺度1 360所需的分析时间大致为1 360T。多尺度滤波总的分析时间为每一个尺度分析时间的累积，即T+2T+3T+…+1 360T，这就使得计算代价极大。同时，反映故障冲击特征的信息往往蕴藏在较小的分析尺度中，分析尺度设定太大会降低计算效率，对提高分析精度也没有帮助。

5 结 论

多尺度形态滤波器中较小尺度的滤波器善于保持信号细节、提取冲击特征，较大尺度的滤波器适用于对信号进行平滑、抑制噪声干扰。在使用中，往往将所有尺度的滤波结果进行算术平均作为多尺度形态滤波器的输出，这一做法会影响故障特征提取的效果。为此，本文使用一种三阶累积量对角切片谱方法对传统的多尺度形态滤波器进行改进，提出一种高速列车万向轴故障识别的方法。本文方法的主要优点在于，三阶累积量对角切片谱具有较强的抑制随机噪声的能力，能够对多尺度形态滤波的结果中存在噪声进一步进行抑制，去除故障无关的频率成分；最优尺度滤波器的选择，能进一步的凸显故障特征。利用台架试验的数据对提出的方法进行了验证，结果表明，本文方法能够从齿轮箱测点的振动信号中有效地提取出万向轴振动的特征，识别正常万向轴与存在不平衡的万向轴。相对于多尺度形态滤波器的分析结果，无论是在谱的清晰度，还是特征频率的振动能量都得到了显著增强。以外，本文方法计算速度快，能够满足实时监测的要求。

[1] 冷扬立，李秋泽，李庆国，等. CRH5型动车组万向轴结构及临界转速分析[J]. 铁道车辆，2010，48(12)：6-11. LENG Yangli，LI Qiuze，LI Qingguo，et al. Analysis of the structure and critical rotating speed of the cardan shafts for CRH5 multiple units [J]. Railway Vehicles，2010，48(12)：6-11.

[2] 张红军，姚远，罗赟，等. CRH5型动车万向轴传动系统技术特征分析[J]. 铁道学报，2009，31(2)：115-119. ZHANG Hongjun，YAO Yuan，LUO Yun，et al. Analysis on technical characteristics of CRH5 cardan drive system [J]. Journal of the China Railway Society，2009，31(2)：115-119.

[3] 姚远，张红军，罗赟. CRH5 型动车万向轴扭转振动分析[J]. 中国铁道科学，2009，30(2)：82-86. YAO Yuan，ZHANG Hongjun，LUO Yun. Analysis on the torsional vibration of cardan shaft on CRH5 motor car [J]. China Railway Science，2009，30(2)：82-86.

[4] 丁建明，林建辉，王晗，等. 万向轴动不平衡检测的二代小波变换奇异值方法 [J]. 机械工程学报，2014, 50(12)：110-117. DING Jianming, LIN Jianhui, WANG Han, et al. Detection of the dynamic unbalance with cardan shaft applying the second wavelet transform and singular value decomposition [J]. Journal of Mechanical Engineering, 2014, 50(12)：110-117.

[5] 阮腾达. CRH5动车组传动系统故障诊断方法研究 [D]. 成都：西南交通大学，2014: 51-73.

[6] CHEN Q, CHEN Z, SUN W, et al. A new structuring element for multi-scale morphology analysis and its application in rolling element bearing fault diagnosis [J]. Journal of Vibration and Control, 2015, 21(4): 765-789.

[7] LI C, LIANG M. Continuous-scale mathematical morphology-based optimal scale band demodulation of impulsive feature for bearing defect diagnosis [J]. Journal of Sound and Vibration, 2012, 331(26): 5864-5879.

[8] 胡爱军，唐贵基，安连锁. 基于数字形态学的旋转机械振动信号降噪方法[J]. 机械工程学报，2006, 42(4):127-130. HU Aijun, TANG Guiji, AN Liansuo. De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter [J]. Chinese Journal of Mechanical Engineering, 2006, 42(4):127-130.

[9] ZHANG L, XU J, YANG J, et al. Multiscale morphology analysis and its application to fault diagnosis [J]. Mechanical System and Signal Processing, 2008, 22(3) :597-610.

[10] 李奕璠，刘建新，林建辉，等. 基于自适应多尺度形态学分析的车轮扁疤故障诊断方法 [J]. 交通运输工程学报，2015，15(1)：58-65. LI Yifan, LIU Jianxin, LIN Jianhui, et al. Fault diagnosis method of railway vehicle with wheel flat based on self-adaptive multi-scale morphology analysis [J]. Journal of Traffic and Transportation Engineering, 2015, 15(1):58-65.

[11] SHEN G, MCLAUGHLIN S, XU Y, et al. Theoretical and experimental analysis of bispectrum of vibration signals for fault diagnosis of gears [J]. Mechanical System and Signal Processing, 2014, 43(1):76-89.

[12] 樊养余，陶宝祺，熊克，等. 舰船噪声的1(1/2)维谱特征提取 [J]. 声学学报，2002, 27(1)：71-76. FAN Yangyu, TAO Baoqi, XIONG Ke, et al. Feature extraction of ship-radiated noise by 1(1/2)spectrum [J]. Acta Acustica, 2002, 27(1):71-76.

[13] 张严，王树勋，李生红. 二次相位耦合的1(1/2)维谱分析 [J]. 电子学报，1996, 24(4)：109-112. ZHANG Yan, WANG Shuxun, LI Shenghong. 1(1/2)dimension spectrum approach to quadratic phase coupling estimation [J]. Acta Electronica Sinica, 1996, 24(4):109-112.

[14] LI B, ZHANG P, WANG Z, et al. Gear fault detection using multi-scale morphological filters [J]. Measurement, 2011, 44(10):2078-2089.

[15] DONG Y, LIAO M, ZHANG X, et al. Faults diagnosis of rolling element bearings based on modified morphological method [J]. Mechanical System and Signal Processing, 2011, 25(3) :1276-1286.

[16] NIKOLAOU N G, ANTONIADIS I A. Application of morphological operators as envelope extractors for impulsive-type period signals [J]. Mechanical System and Signal Processing, 2003, 17(6):1147-1162.

[17] 李兵，张培林，米双山，等. 机械故障信号的数字形态学分析与智能分类 [M]. 北京：国防工业出版社，2011.

Diagonal slice spectrum lifted morphology filtering method and its application in cardan shaft fault detection

LI Yifan1, LIN Jianhui2, LIU Weiwei1

(1. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. Traction Power State Key Lab, Southwest Jiaotong University, Chengdu 610031, China)

Aiming at solving the problem that the arithmetic average of filtering results is carried out over all scales in multi-scale morphological filter, a third-order cumulant diagonal slice spectrum method was proposed to improve the conventional multi-scale morphological filter for its use in the fault detection of high speed railway cardan shaft. The multi-scale filtering of the signals collected by the vibration sensor installed on a gearbox was conducted in advance to obtain the filtering results in different scales. Then the third-order cumulants and corresponding diagonal slices of the filtered signals were calculated, and the optimal scale which can best highlight the fault characteristics was selected based on a characteristic frequency intensity coefficient. As a consequence, the arithmetic average problem of multi-scale morphological filter is avoided. A test rig experiment was conducted on an unbalance test bench of cardan shaft. The results show that the proposed method is effective to identify the fault features of fundamental frequency and multiple frequencies caused by the unbalance of cardan shaft. Comparing with the traditional multi-scale morphological filter, the method is better to manifest fault features.

high speed train, cardan shaft, multi-scale morphology filtering, diagonal slice spectrum

国家自然科学基金资助项目(61134002)；中央高校基本科研业务费(SWJTU2682014BR001EM)

2015-10-08 修改稿收到日期： 2016-03-20

李奕璠 男，博士，讲师，1985年4月生

U270

A

10.13465/j.cnki.jvs.2017.10.003