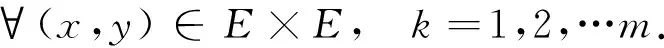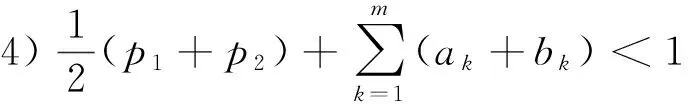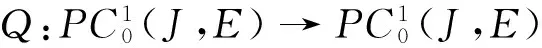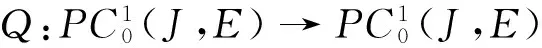Banach空间含导数项的二阶脉冲微分方程的解
尚亚亚, 史静文, 李永祥
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
Banach空间含导数项的二阶脉冲微分方程的解
尚亚亚, 史静文, 李永祥*
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
讨论了抽象空间中非线性项含一阶导数的二阶脉冲微分方程边值问题
Banach空间; 非紧性测度; 凝聚映射; 不动点定理
本文考虑Banach空间中非线性项含一阶导数的二阶常微分方程两点边值问题(BVP)
(1)
解的存在性,其中J=[0,1],f∈C(J×E×E,E),Ik∈C(E×E,E)是脉冲函数,k=1,2,…,m,0 脉冲微分方程是描述在确定时刻其状态发生瞬间改变的数学模型,具有广泛的应用背景,如生物技术、生态平衡、人口控制及经济发展等,成为近年来一个重要的研究领域[1-4].对于BVP(1)的特殊情形Ik=0,即边值问题 当E=R时,文献[5-6]应用锥上的不动点指数理论获得了BVP(2)正解及多正解的存在性;文献[7]对非线性项f(t,x,y)提出关于y的增长条件(Nagumo条件),运用上下解方法讨论了其解的存在性;文献[8]在锥上建立了一个新的泛函形式的不动点定理,在f满足一定的增长条件下获得了此问题至少存在3个正解. 在抽象空间中,文献[9]考虑了‖f(t,x,y)‖≤M(M>0为常数)时BVP(2)解的存在性,条件较强.由于有限维与无限维空间的本质差异,BVP(2)对应的线性问题的解算子不再具有紧性,而且对u′的处理比较困难,因而此类问题的研究所获结论相对较少,发展也较为缓慢. 文献[4]在抽象Banach空间中运用上下解方法和单调迭代技巧研究了如下的二阶脉冲微分方程边值问题 解的存在性,并建立了极大解和极小解的存在性定理,但其非线性项与u′无关. 受上述文献启发,本文在一般的抽象空间中考虑BVP(1)解的存在性与唯一性.通过选取适当的工作空间及等价范数,在较一般的条件下用新的非紧性测度估计技巧并结合Sadovskii不动点定理,得到了解及正解的存在性结果.此外,在非线性项f(t,x,y)及脉冲函数Ik(x,y)满足Lipschitz条件时,运用Banach不动点定理获得了该问题的唯一解. PC1(J,E)= 易证,PC(J,E)与PC1(J,E)分别按范数 及 构成Banach空间. 若函数u∈PC1(J,E)∩C2(J′,E)满足BVP(1)中所有等式,则称其为BVP(1)的一个解. 为了方便起见,本文取PC1(J,E)的子空间 故 构成Banach空间. 引理 1[10]设D⊂E有界,则存在D的可列子集D0,使α(D)≤2α(D0). 引理 2[11]设D={xn}⊂L[J,E]有界可数,则存在g∈L[J,R+]使得对一切{xn}∈D,‖xn‖≤g(t),a.e.t∈J,则α(D(t))∈L[J,R+],且 引理 3[12]设B⊂PC(J,E)有界,在每个Jk上等度连续,则α(B(t))在J上连续,且 2) 对∀t∈J,α(B(t))≤αPC(B′),αPC(B′(t))≤αPC(B′). 故由非紧性测度的定义易知 按非紧性测度的定义,2)成立.证毕. 由于非线性问题与线性问题密切相关,对∀h∈PC(J,E),先考虑BVP(1)对应的线性问题(LBVP) 解的存在性,其中yk∈E,k=1,2,…,m. (5) 的解,其中 继续在[0,t]上积分有 (6) 代入边界条件有 将(7)式代入(6)式中,即(5)式成立. 且容易验证 因此 是LBVP(4)的解.证毕. (8) 则Q连续.对上式关于t求导,即 (9) 引理 6 设E为Banach空间,f:J×E×E→E与Ik:E×E→E连续.若f≥θ,Ik≥θ,则BVP(1)的解u(t)满足:u(t)≥θ. 证明 由于BVP(1)的解等价于算子Q的不动点,又因f≥θ,Ik≥θ,G(t,s)≥0,根据算子Q的表达式,显然u(t)=Qu(t)≥0. 定理 1(Sadovskii不动点定理)[13]设X为Banach空间,Ω⊂X为有界凸闭集,Q:Ω→Ω为凝聚映射,则Q在Ω中有不动点. 定理 2 设E为Banach空间,f:J×E×E→E与Ik:E×E→E连续,若下列条件成立: 1)f把J×E×E中的有界集映为E中的有界集,Ik把E×E中的有界集映为E中的有界集,且存在常数L1,L2≥0及Mk1,Mk2≥0,使得对任意的有界集Di⊂E(i=1,2)有: 其中 2) 存在常数p0>0,p1,p2≥0,使得 3) 对每个Ik,存在常数ck>0及ak,bk≥0,使得 则BVP(1)至少有一个解. (10) 再由引理1,存在可数集B1={un}⊂B,使得 (11) 而Q′(B1)为PC(J,E)中的等度连续集,因此 (12) 对∀t∈J,结合条件1)、引理2及引理4,于是 因此 (13) 结合(10)~(13)式及引理4,则 这里 (14) 令 即 定理 3 设E为Banach空间,f:J×E×E→E及Ik:E×E→E连续且满足条件: 5) 存在常数c1,c2>0及Nk1,Nk2>0,使得对∀t∈J,x1,x2,y1,y2∈E有: 则BVP(1)存在唯一解. 那么 因此 定理 4 设E为Banach空间,f:J×E×E→E与Ik:E×E→E连续.若条件1)~4)成立且满足f≥θ,Ik≥θ,则BVP(1)至少有一个正解. 证明 由定理2,1)~4)成立,即BVP(1)至少有一个解u0(t).又因f≥θ,Ik≥θ,由引理6,u0(t)≥θ,因此BVP(1)至少存在一个正解. 注 1 若BVP(1)中Ik(x,y)=0,即不含脉冲的情形,BVP(1)便退化为BVP(2),按照本文的论述方法可得类似结论,其结果在抽象空间也是新的. 注 2 工作空间及等价范数的选取对于研究的问题至关重要,不仅可以简化计算,而且可以得出较好的结果.鉴于对u′处理的难度,部分非线性项含导数的边值问题,可按本文的办法进行相关研究.比如,可进一步讨论问题 解的存在性,其中 为Fredholm积分算子,K(t,s)∈C(J×J,R+). [1] LAKSHMIKANTHAM V, BAINOV D D, SIMEONOV P S. Theory of impulsive differential equations[J]. Aequationes Mathematicae,1989,6:288. [2] GUO D J. A class of second-order impulsive integro differential equations on unbounded domain in a Banach space[J]. Appl Math Comput,2002,125:59-77. [3] LIN X N, JIANG D Q. Multiple positive solutions of Dirichlet boundary value problems for second order impulsive differential equations[J]. J Math Anal Appl,2006,321:501-514. [4] 范虹霞. Banach空间中二阶脉冲微分方程边值问题极解的存在性[J]. 兰州交通大学学报,2012,31(3):154-157. [5] 邹玉梅,崔玉军. 含有一阶导数的二阶边值问题的正解[J]. 应用数学学报,2009,32(1):106-111. [6] AGARWAL R P, O’REGAN D, YAN B Q. Multiple positive solutions of singular Dirichlet second-order boundary-value problems with derivative dependence[J]. J Dyn Control Sys,2009,15(1):1-26. [7] HENDERSON J, THOMPSON H B. Existence of multiple solutions of second order boundary value problems[J]. J Diff Eqns,2000,166:443-454. [8] BAI Z B, GE W G. Exsistence of three positive solutions for some second-order boundary value problems[J]. Comput Math Appl,2004,48:699-707. [9] MÖNCH H. Boundary value problems for nonlinear ordinary differential equations of second order in Banach spaces[J]. Nonlinear Anal,1980,4(5):985-999. [10] 李永祥. 抽象半线性发展方程初值问题解的存在性[J]. 数学学报:中文版,2005,48(6):1089-1094. [11] HEINZ H P. On the behaviour of measure of non-compactness with respect to differentiation and integration of vector-valued functions[J]. Nonlinear Anal,1983,7:1351-1371. [12] GUO D J, LAKSHMIKANTHAM V, LIU X Z. Nonlinear Integral Equations in Abstrat[M]. Amsterdam:Kluwer Academic Publishers,1996. [13] DEMILING K. Nonlinear Functional Analysis[M]. New York:Springer-Verlag,1985. [14] LI Y X, JIANG X Y. Positive periodic solutions for second-order ordinary differential equations with derivative terms and singularity in nonlinearities[J]. J Funct Spaces Appl,2012,2012(19):4520-4562. [15] 何志乾. 奇异二阶Neumann边值问题正解的存在性[J]. 四川师范大学学报(自然科学版),2015,38(2):190-193. [16] 覃燕梅,罗卫华,孔花,等. 二阶Fredholm积分微分方程的有限差分配置法[J]. 四川师范大学学报(自然科学版),2016,39(4):531-535. 2010 MSC:34B37 (编辑 余 毅) The Solutions for Second Order Impulsive Differential Equations with Dependence on the Derivative Terms in Banach Spaces SHANG Yaya, SHI Jingwen, LI Yongxiang (CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu) In this paper, we consider the existence and uniqueness solutions for second order impulsive differential equations with dependence on the first order derivativein Banach spaces, where,f∈C(J×E×E,E),Ik∈C(E×E,E),k=1,2,…,m. By choosing proper working space and equivalent norm, while the nonlinear termf(t,x,y) andIk(x,y) satisfy more general non-compactness measure conditions, we obtain the existence results of solutions and positive solutions combining with the estimation skills of the non-compactness measure and the Sadovskii fixed-point theorem. Besides, we discuss the uniqueness of the solutions of this boundary value problem. Banach space; non-compactness measure; condensing mapping; fixed-point theorem 2016-07-08 国家自然科学基金(11261053)和甘肃省自然科学基金(1208R-JZA129) O A 1001-8395(2017)01-0045-06 10.3969/j.issn.1001-8395.2017.01.007 *通信作者简介:李永祥(1963—),男,教授,主要从事非线性泛函分析的研究,Email:liyx@nwnu.edu.cn 解的存在性与唯一性,其中f∈C(J×E×E,E),Ik∈C(E×E,E),k=1,2,…,m.通过选取恰当的工作空间及等价范数,在非线性项f(t,x,y)及脉冲函数Ik满足较一般的非紧性测度条件下,结合新的非紧性测度估计技巧与凝聚映射的Sadovskii不动点定理,得到解及正解的存在性结果.此外,进一步讨论该问题唯一解的存在性.

1 预备知识
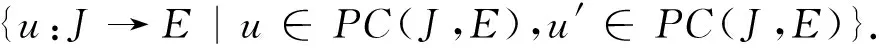

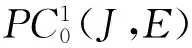
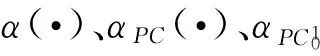
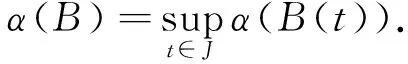

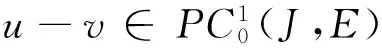


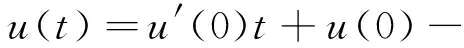
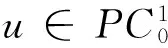
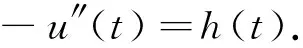
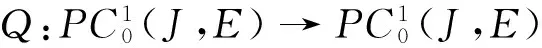

2 主要结果及证明