A Constructive Exposition on Simple Forcings and Countable Forcings
ZHU Huiling, ZHENG Fudan
(Guangzhou College, South China University of Technology, Guangzhou 510800, Guangdong)
A Constructive Exposition on Simple Forcings and Countable Forcings
ZHU Huiling, ZHENG Fudan
(GuangzhouCollege,SouthChinaUniversityofTechnology,Guangzhou510800,Guangdong)
In this paper, we explain two classes of forcings: simple forcings and countable forcings. A couple of examples that mathematician are interested in are studied as special cases of forcing. General theorems about these two classes are proved.
simple forcing; countable forcing; partial order; dense embedding; models
1 Introduction
In modern set theory, forcing is an effective technique in obtaining independent results. Since its discovery by Cohen[1], the application of forcing has been extended to many branches of mathematics. In particular, those branches with infinite objects. However, the highly technical feature of forcing also kept it away from being understood for many mathematicians. There are a couple of standard textbooks about forcing, for instance, [2-3]. These textbooks provide a detailed treatment of forcing and are suitable for those with basic knowledge about set theory. However, people believe that although the general theory of forcing is not an open research problem, it remains an open exposition problem, as illustrated in [4]. Therefore, logicians attempted to make the system of forcing more accessible to mathematicians who are interested in independent proof. For example, [4] put much effort in making forcing “transparent”. We wish to follow the line and make explanations of some more facts of forcing. The beginners of forcing are referred to [5-7] for basic notions and notations. Readers with interests in applications are referred to [8-9].
2 Simple Forcings
A trivial forcing consists of a singleton. Such a forcing will not affect the ground model at all. Mathematicians are familiar with many kinds of partial orders, for instance, finite partial orders, linear orders and lattices. In a sense that we will explain below, these partial orders are all simple, as they are reduced to a trivial forcing.
Forcing extends models of set theory, preserving certain features of the initial model and violating some others. In the study of forcing, it is crucial to analyze the properties of given partial orders. The general theory of forcing thus involves comparing two partial orders, finding similarities as well as differences between them.
The following theorem can be found in [2]:
Theorem 2.1 If there is a functionf:→satisfying:
1)Orderpreserving:Ifp≤p′,thenf(p)≤f(p′);
2)Density:Foranyq∈,thereissomep∈withf(p)≤q;
3)Non-triviality:Ifpandqareincompatible,thenf(p)andf(q)areincompatible.
Thenandgeneratesthesamegenericextension.
Ifanytwoanyelementsofarecompatible,thencanbedenselymappedintoatrivialforcing.
Corollary2.2Suchafunctionfiscalledadensemapping.Aninjectivedensemappingisusuallycalledadenseembedding.Wealsosaythatandareforcingequivalent,witnessedbyf.
ProofConsider{{Ø},=},whichisanexampleofatrivialforcing.Letf(p)=Øforanyp.ThenthefirsttworequirementsofTheorem2.1hold.Thethirdrequirementholdssincetheassumptionfails.
Asaresult,anylinearorderorsemi-lowerlatticeisdenselymappedintoatrivialforcing.
Afiniteforcingisactuallyatomic,namely,everyconditionextendstoanatom.Sinceeverygenericfilterhastoincludealltheatoms,ithastoincludethewholepartialorder.Thentheforcingistrivialbydefinability.
3 Cohen Forcing
The first and most notable forcing was Cohen forcing[1], which uses finite segments to approximate a real. Namely, the partial order is (2<ω,⊇). A maximal collection of conditions which are mutually consistent will define a function fromωto 2. In set theory, reals are identified with such functions. More precisely, any such function corresponds to an irrational number in the inteval (0,1). Associated with the product topology, such a space is called the Cantor space. There are other variations of the space of reals. For instance,ωωwith the product topology is called the Baire space.
Cohen forcing is countable. In fact, any nontrivial countable partial orders yields the same generic extension. Though this is a known result, there is no text which present a direct construction. Therefore we explain it here in an accessible way by defining a dense embedding explicitly.
4 Examples of Countable Forcings
Before we proceed to the general case, let us start with some concrete examples.
Theorem 4.1 There is a dense embeddingf:(4<ω,⊇)→(2<ω,⊇).
Proof Letπ:4→22be a bijection. For instance,π(0)=〈00〉,π(1)=〈01〉,π(2)=〈10〉,π(3)=〈11〉. Definefas follows:
It is obvious thatfis a nontrivial embedding.
To show thatfis dense, letσ∈2<ω. Ifσhas an even length, letσ′=σ; otherwise, letσ′=σ⌒0. Letτ∈4<ωbe defined as:
Thenf(τ)=σ′⊇σ.
Theorem 4.2 The forcing (3<ω,⊇) can be densely embedded into (2<ω,⊇).
Proof Fixπwithπ(0)=〈0〉,π(1)=〈10〉,π(2)=〈11〉. Let
Notice that for everyσ∈2<ω, one can trace the digits from the root, find pieces of type 〈0〉, 〈10〉 or 〈11〉, and if the last remaining digit is 1, extendσwith a 0 to the tail. For instance, givenσ=〈0010110〉∈2<ω, considerτ=〈00120〉, thenh(τ)=σ. Givenσ=〈00101101〉, we first extend it toσ′=〈001011010〉, and letτ=〈001201〉, thenh(τ)=σ′<σ.
It is clear thathis a dense embedding.
Theorem 4.3 There is a dense embedding from (ω<ω,⊇) into (2<ω,⊇).
Proof First fix a codingπ:ω→2<ω. A canonical coding is the following:π(0)=Ø,π(1)=〈0〉,π(2)=〈1〉,π(3)=〈00〉,π(4)=〈01〉,π(5)=〈10〉,π(6)=〈11〉 etc.
Defineg:(ω<ω,⊇)→(3<ω,⊇) as follows:
gis clearly injective and order preserving.gis actually surjective and hence dense. One can trace the digits in 3<ωand find the suitable preimage. For instance, the sequence 〈0020210221211〉 has preimage 〈315026〉.
Combininggwith the dense embeddinghin Theorem 4.2, one gets a dense embedding from (ω<ω,⊇) into (2<ω,⊇).
5 The General Theorem
In this section, we prove the general theorem that two nontrivial countable forcings are actually equivalent.
A forcing partial order is usually assumed to be both separative and atomless. These requirements are used to keep the forcing away from being trivial. Namely, an atom in a forcing adds no generic object as it contributes no diversity to the forcing. Also, if a forcing is non-separative, then it contains some segments of linear ordering, which can be deleted without affecting the property of forcing.
Theorem 5.1 For every separative atomless countable partial order,thereisacountablepartialorder,whichcanbedenselyembeddingintobothand(2<ω,⊇).
WeprovefirstalemmaontheCohenforcing.
Lemma5.2Foranyσ∈(2<ω,⊇), 2≤n≤ω,thereisamaximalantichainbelowσwithcardinalityn.
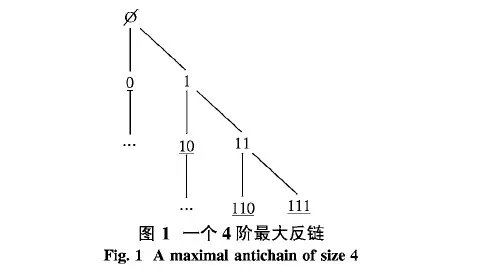

ProofForeachn<ω,considertheset
InFigure1,theunderlinednodesformamaximalantichainofsize4.
Ifn=ω,considertheset
InFigure2,theunderlinednodesformamaximalantichainofsizeω.
ProofofTheorem5.1List={sm:m∈ω}.Firstly,wefindamaximalantichainA0={pn:n∈I0},whereI0isanindexset.Makesurethatthereissomepn≤s0andA0hasatleast2elements.
ItisclearthatA1isanantichain.Itisactuallymaximal.Foranyr,thereissomepncompatiblewithr.Letq≤pn, q≤r.Letpnkbecompatiblewithq,sayq′≤q, q′≤pnk.Thenq′≤rwitnessthatrandsomepnkarecompatible.
Inductively,atstepn,oneconstructamaximalantichainbelowanyconditionfoundatthepreviousstep.AndletAncollectalltheseconditionsfoundatstepn.Byinduction, Anisamaximalantichain.
Thisprocesscanbecarriedonasisseparativeandatomless:atstepm,thereissomea∈Am-1suchthatsnandaarecompatible.letr≤sm, r≤a.Sinceisatomless,wemayassumethatr Nowdefine=∪{Am:m<ω}.Themappingfromtoissimplyinclusion.Toseethatisadensesubforcing,letsm∈,thenthereissomea∈Am⊆suchthata≤sm. Themappingfrominto(2<ω,⊇)isdefinedasfollows:firstidentifyA0withamaximalantichainin(2<ω,⊇).ThiscanbeguaranteedbyLemma5.2,as2≤|A0|≤ω.Inductively,identifyAnwithamaximalantichainin(2<ω,⊇)whilepreservingthepartialorder. Toseethedensity,onecanalsodealwithconditionsin(2<ω,⊇)diagonally,aswedidwith. Remark5.3Theaboveproofisactuallythetypical“backandforth”argument,whichiseffectiveindealingwithcountableobjects. Inthissection,weconsidersomeproblemsforfuturestudy. 1)Aretheresemi-upperlatticeswhichareusefulinthesenseofforcing? 2)Foragivenalgebraicstructure,forinstance,aringorafield,isthereacanonicalwaytoassociateaforcingtoit? 3)Fortopologicalspaceswithdifferentseparability,isthereaclassificationtheoryinthewayofforcing? [1] COHEN P J. The independence of the continuum hypothesis. I.[J]. Proc Natl Acad Sci,1963,50:1143-1148. [2] JECH T. Set theory[C]//Springer Monographs in Mathematics. New York:Springer-Verlag,2003. [3] KUNEN K. Set theory[C]//Studies in Logic and the Foundations of Mathematics,102. Amsterdam:North-Holland Publishing,1980. [4] CHOW T Y. A beginner’s guide to forcing[C]//Communicating Mathematics,479. Providence:Am Math Soc,2009:25-40. [5] JECH T. Multiple forcing[C]//Cambridge Tracts in Mathematics,88. Cambridge:Cambridge University Press,1986. [6] JECH T. What is … forcing?[J]. Notices Am Math Soc,2008,55(6):692-693. [7] JECH T. Set theory, with particular emphasis on the method of forcing[C]//Lecture Notes in Mathematics,217. New York:Springer-Verlag,1971. [8] TODORCHEVICH S, FARAH I. Some applications of the method of forcing[C]//Yenisei Series in Pure and Applied Mathematics. Moscow:Lycee,1995. [9] JECH T. Abstract theory of abelian operator algebras:an application of forcing[J]. Trans Am Math Soc,1985,289(1):133-162. 关于单纯力迫和可数力迫的构造性阐述 朱慧灵, 郑馥丹 (华南理工大学 广州学院, 广东 广州 510800) 解释了2类力迫,即单纯力迫和可数力迫.将数学家经常遇到的几类偏序作为力迫的特殊情况加以研究.证明了关于这2类力迫的一般性结论. 单纯力迫; 可数力迫; 偏序; 稠密嵌入; 模型 O144.3 A 1001-8395(2017)01-0018-04 2015-10-03 国家自然科学基金(11401567) 朱慧灵(1985—),男,副教授,主要从事数理逻辑及其应用的研究,E-mail:zhuhl02@gmail.com Foundation Items:This work is supported by National Natural Science Foundation of China (No.11401567) 10.3969/j.issn.1001-8395.2017.01.003 (编辑 周 俊) Received date:2015-10-03 2010 MSC:03E17; 03E35; 03E506 Futher Problems

