一种无传播误差的差分隐私频繁项集挖掘算法

廖 勇, 冯 山

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

一种无传播误差的差分隐私频繁项集挖掘算法

廖 勇, 冯 山*

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

差分隐私保护具有背景知识无关性,在隐私数据挖掘中可以抵御任意形式的攻击.基于干扰的差分隐私保护算法SmartTrunc存在如下问题:1) 传播误差导致挖掘结果的可用性降低;2) 全局敏感度大导致扰动所需噪声量预期值较大.为此,DFDP算法通过真实频繁k项集而不是扰动后的频繁k项集生成候选k+1项集,以彻底消除传播误差.同时,它通过一种新的函数映射将全局敏感度降为1,以减少干扰所需添加的噪声量.理论分析与实验结果均表明,DFDP算法能有效提升挖掘结果的可用性,同时所需添加的噪声量更少.

频繁项集; 隐私保护; 差分隐私; 拉普拉斯扰动; 传播误差

频繁项集挖掘是数据挖掘研究领域的一个重要研究分支,是关联规则挖掘的基础.当事务数据集含有敏感数据时,直接发布频繁项集及其真实支持度计数可能泄露用户的隐私信息.因此,需对频繁项集挖掘进行必要的隐私保护.传统的隐私保护模型一般需特殊的攻击假设,并随新型攻击的出现而不断改进完善,不能提供及时、有效的安全保障,如K-匿名模型[1]不能抵御链接攻击[2],其安全性与攻击者掌握了多少背景知识相关,且不能严格证明和定量分析其隐私保护水平.背景知识是指除隐私保护对象外的所有其他与隐私保护模型相关的信息,如其他数据对象的信息、隐私保护模型和实现算法等.

为此,近年来研究人员试图寻找与背景知识无关的隐私保护模型以抵御任意形式的攻击;差分隐私保护模型[3]就在这一背景下产生.其攻击模型为:最坏情况下,攻击者已获得除隐私保护对象外的所有背景知识,隐私保护对象的隐私信息仍能得到保护.差分隐私保护模型有严格的数学理论支撑,可严格证明和定量分析其隐私保护水平;一提出就被应用于隐私保护频繁项集挖掘[4-8].

文献[8]提出的SmartTrunc算法存在如下问题:1) 利用噪声频繁项集生成候选项集所产生的传播误差降低了挖掘结果的可用性,双阈值法在一定程度上减少了传播误差,但并不能彻底消除;2) 一次性计算所有候选项集的真实支持度计数,导致全局敏感度较大,且与事务记录长度相关;3) 截断长事务记录减小全局敏感度的量有限,且仅对短事务记录比例较大的事务数据集性能较好,扩展性较差.为此,本文提出了一种无传播误差的差分隐私频繁项集挖掘算法DFDP.DFDP无传播误差,全局敏感度更小,不需截断长事务记录,适用范围更广.

1 相关概念

性质 1(频繁项集的先验性质) 若项集X频繁,其所有非空子集一定频繁;否则,其所有超集一定非频繁.

定义 1(传播误差) 在隐私算法中,由于算法本身的作用使得原本频繁的项集X标记为非频繁,而导致X的所有超集被非频繁化的挖掘误差称为传播误差.

设事务数据集的集合D={Di|1≤i≤+∞},其中,Di(1≤i≤+∞)是具有相同属性结构的事务数据集,|Di|表示Di中事务记录总数.Rd={R1,R2,R3,…}是d维实数向量空间,其中Ri=〈ri1,ri2,…,rid〉是d维实数向量.

定义 2(相邻数据集) 对任意D1,D2∈D,满足D1⊂D2或D2⊂D1,D1与D2不同事务记录的条数记为|D1ΔD2|.|D1ΔD2|=1时,D1、D2称为相邻数据集.

设M为一随机算法,D1、D2为D中任意相邻数据集.M(D1)和M(D2)分别表示M在D1和D2上所有可能输出结果的范围.在函数映射fM:D→Range(M)中,Range(M)表示M在D上所有可能输出结果的范围.

定义 3[3](差分隐私) 对D中任意相邻数据集D1、D2及任意z∈Range(M),若M满足(1)和(2)式,则M满足s-差分隐私.

(1)

(2)

其中,s为隐私保护预算,Pr[M(D1)=z]和Pr[M(D2)=z]分别是M(D1)=z和M(D2)=z的概率.

对差分隐私而言,s越大,满足(1)和(2)式越容易.理论上,可取到合适的s来保证在D1中添加或删除一条事务记录时,M在D1及其相邻数据集D2上输出同一结果的概率无明显变化.

噪声扰动是差分隐私中的常用技术.它通过向查询或统计结果添加噪声来保护隐私,但噪声过多会降低结果的可用性,过少又没有足够的安全保障.为了更准确地确定需添加的噪声量,差分隐私用全局敏感度和隐私保护预算共同决定噪声量的大小.

定义 4[3](全局敏感度) 设函数Q:D→Rd,D1、D2为D中任意相邻数据集,则Q(D1)与Q(D2)之间的差异值称为Q在相邻数据集D1和D2上的敏感度.相应地,D中所有相邻数据集中的最大差异值称为Q在D上的全局敏感度,记为

(3)

其中,‖Q(D1)-Q(D2)‖1是Q(D1)与Q(D2)之间的1-阶范数距离,ΔQ由Q本身定义的映射关系决定,与D无关.

拉普拉斯扰动是差分隐私中常用的扰动方法.拉普拉斯概率密度函数[9]

μ是位置,b(b>0)是尺度.μ=0时的概率密度函数记为p(x),对应的分布记为Lap(b).显然p(x)>0,图像关于x=0对称,越靠近x=0点函数值越大(图1).故用Lap(b)扰动时,越靠近0的值的取值概率越大.

定理 1[10](拉普拉斯扰动原理) 设函数Q:D→Rd的全局敏感度为ΔQ.隐私保护预算为s,随机变量Yi(1≤i≤d)相互独立且服从Lap(ΔQ/s)分布.对任意Dj(Dj∈D),若随机算法M满足(4)式,则M满足s-差分隐私.

(4)

对Lap(ΔQ/s),由图1知,ΔQ越大,p(x)的图像越扁平,添加的噪声预期值越大.同理,s越大,添加的噪声预期值越小;即噪声量的大小与ΔQ成正比,与s成反比.

性质2表明,M较复杂时,只要M涉及隐私的子序列均满足差分隐私,M就满足差分隐私.

2 SmartTrunc算法

SmartTrunc[8]和Apriori[12]都利用性质1迭代生成频繁项集,其不同在于生成候选k+1项集时,前者利用噪声频繁k项集,后者利用真实频繁k项集.若真实频繁k项集X在SmartTrunc中标记为非频繁,由性质1,X的所有超集也非频繁.故SmartTrunc存在传播误差,这降低了挖掘结果的可用性.为此,文献[8]引入双阈值法以在一定程度上减少传播误差,其中生成候选项集的阈值小于生成频繁项集的阈值;但双阈值法并不能彻底消除传播误差.

例如,D1是某文具店的部分购物事务记录(表1),其生成候选项集的阈值和生成频繁项集的阈值分别为2和3.D1的真实频繁项集如表2所示.在SmartTrunc下,频繁k项集X的真实支持度计数的扰动结果是随机的,则X的噪声支持度计数<2时,将不会用于生成候选k+1项集,直接导致X的所有超集非频繁.如表2中{A}的噪声支持度计数<2时(如1.7),{A}就不会用于生成候选2项集,直接导致真实频繁项集{AB}非频繁.故传播误差仍存在.

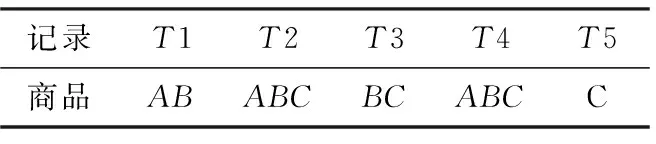
表 1 数据集D1

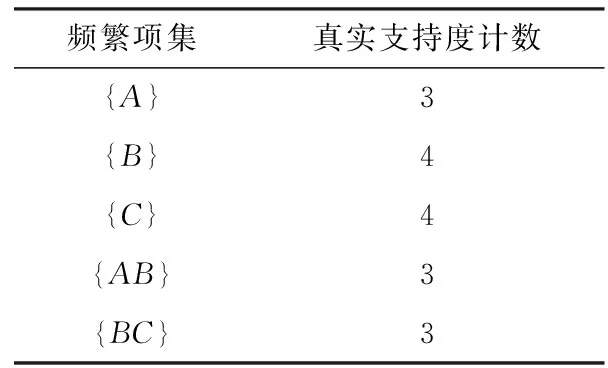
表 2 D1的真实频繁项集

3 DFDP算法

对D中的事务数据集D1,设最小支持度计数阈值为min_count,隐私保护预算为s,Ck为候选k项集集合,Lk为真实频繁k项集集合,Yk为噪声频繁k项集集合,|Ck|为Ck中项集总数.

3.1 基本思想与计算过程

3.1.2 计算过程 1) 扫描D1得到C1;2) 由C1生成L1;3) 用Lap(1/s)扰动C1中项集的真实支持度计数;4) 据C1及噪声支持度计数生成满足min_count的Y1;5) 用L1生成C2;6) 用C2成L2;7) 用Lap(1/s)扰动C2中项集的真实支持度计数,据C2及噪声支持度计数生成满足min_count的Y2,然后用L2生成C3,再用C3生成L3;8) 重复7),Lk=Ø时结束;9) 输出Y=∪kYk.

3.1.3 DFDP算法 DFDP的简要描述如下:

输入:事务数据集D1,最小支持度计数阈值min_count,隐私保护预算s

输出:D1的噪声频繁项集集合Y

C1=candidate_1_itemsets(D1);//D1→C1

for ∀t∈D1{//扫描D1进行计数

Ct1=subset(C1,t);//t的1项子集

for ∀c∈Ct1{c.count++;}

}

L1={c∈C1|c.count≥min_count};

for ∀c∈C1{c.count=c.count+Lap(1/s);}

Y1={c∈C1|c.count≥min_count};

for (k=2;Lk-1≠Ø;k++){

Ck=gen_candt(Lk-1);//Lk-1生成Ck

for ∀t∈D1{

Ctk=subset(Ck,t);//t的k项子集

for ∀c∈Ctk{c.count++;}

}

Lk={c∈Ck|c.count≥min_count};

if (Lk≠Ø){

for∀c∈Ck{c.count=c.count+Lap(1/s);}

Yk={c∈Ck|c.count≥min_count};

}

}

returnY=∪kYk;//输出噪声频繁项集

3.2 隐私分析 设D1为D中的事务数据集,D1的所有候选集的集合记为∪kCk,|∪kCk|是∪kCk中项集总数.项集Xi∈∪kCk(1≤i≤|∪kCk|)对应的真实支持度计数查询函数为Qi,ΔQi=1(1≤i≤|∪kCk|).对D1中的项集Xi的真实支持度计数添加Lap(1/s)噪声的算法记为Mi,即

Yi(1≤i≤|∪kCk|)是服从Lap(1/s)分布的随机变量,则Mi满足s-差分隐私.对D中任意相邻数据集D1、D2,Qi(D1)和Qi(D2)分别是Xi在D1和D2中的真实支持度计数,Range(Mi)是Xi在D上所有可能的噪声支持度计数的集合.

证明Mi满足s-差分隐私的证明如下.

对D中任意相邻数据集D1、D2及Xi的任意噪声支持度计数z∈Range(Mi)有

Yi为z-Qi(D1)和z-Qi(D2)的概率比值就是其概率密度函数值之比,故

因p(x)=1/(2b)×exp(-|x|/b),b=1/s,故

由不等式|a|-|b|≤|a-b|有

又因

则

故

因此

成立.

同理,因

因此

成立.

综上所述,由定义3,Mi满足s-差分隐私.

因对∪kCk中每个项集的真实支持度计数添加Lap(1/s)噪声均满足s-差分隐私,由性质2,DFDP满足|∪kCk|×s-差分隐私.|∪kCk|无法预先确定,DFDP没有给定总的隐私保护预算,而是为每次添加噪声的操作分配等额的隐私保护预算s.由(1)和(2)式知,只要s大小合适,DFDP仍具有很好的隐私性.

3.3 实例 数据集D1如表1所示,最小支持度计数阈值设为3,其真实频繁项集如表2所示.在DFDP下,扰动后的候选项集如表3所示,噪声频繁项集如表4所示.

表 3 DFDP扰动后的候选项集

结合算法1,对比表2和表4可知,表2中真实频繁项集{A}在DFDP中没有挖掘出来,是由差分隐私算法本身的噪声扰动特性引起的,而不是由传播误差引起的.由L1生成C2时,C2={{AB},{BC},{AC}},因{AB}和{BC}的噪声支持度计数大于最低阈值,它们是频繁的,而{AC}扰动后依然非频繁.在DFDP下,{A}的非频繁并没有导致真实频繁项集{AB}的频繁性失真.由性质1,用Yk生成Ck+1会导致传播误差.故在SmartTrunc下,用表4中的Y1生成C2时,因Y1不包含{A}而直接导致{AB}非频繁.显然,它偏离了DFDP的挖掘结果(表4),故SmartTrunc结果的可用性低于DFDP.

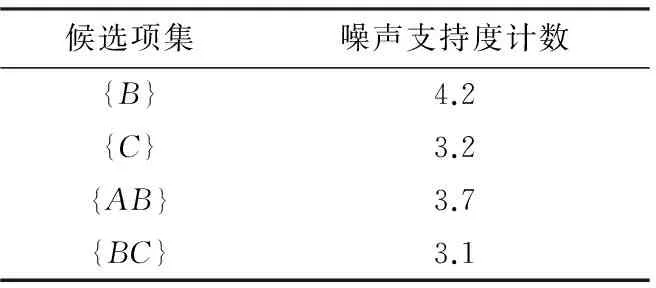
表 4 DFDP的噪声频繁项集

4 误差分析与实验结果

4.1 误差分析 由拉普拉斯扰动原理,ΔQ较小时添加的噪声预期值也较小.隐私保护预算s减小时Lap(1/s)的密度曲线更扁平,添加的噪声预期值更大,隐私保护级别更高.为了更准确地评估和分析误差,本文用平均绝对误差(δMAE)衡量隐私保护预算s对支持度计数的影响,用F-score衡量噪声频繁项集的可用性.

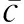
(5)

从统计意义上讲,δMAE越小,隐私算法挖掘结果的支持度计数误差越小.

定义 6[13](F-score) 设Up为差分隐私下的噪声频繁项集集合,Uc为真实频繁项集集合.Up∩Uc是Up和Uc的交集,|Up|、|Uc|和|Up∩Uc|分别是Up、Uc和Up∩Uc中项集的个数,则

(6)

显然,F-score越大,Up和Uc的交集越大,即差分隐私下的噪声频繁项集的可用性越高.

4.2 实验结果 通过仿真实验结果来比较DFDP和SmartTrunc挖掘结果的误差和可用性.实验代码用C语言完成,环境为Inter(R) Core(TM) i5-2400 CPU@3.10 GHz,2 GB内存,Windows 7.所用数据是某超市某月的部分销售数据(http://www.datatang.com/data/44163),包括300条事务记录和50种商品,平均每条事务记录包含3种商品,且短事务记录居多.

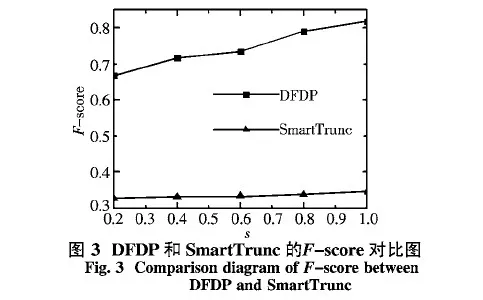
2个算法中Lap(1/s)取值均限制为[-10,10],生成频繁项集的阈值均设为4.SmartTrunc生成候选项集的阈值设为2,并截断商品多余7种的事务记录.隐私保护预算s将从0.2渐变到1,每个s值重复试验5次并取其平均值作为最终结果(保留3位小数).实验结果的δMAE和F-score及其对比分别如图2和图3所示.

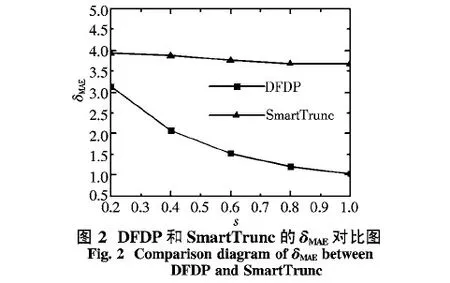
由图2可知,隐私保护预算s越大，δMAE越小；即隐私算法挖掘结果的支持度计数误差越小.DFDP中的δMAE明显小于SmartTrunc中的δMAE,即DFDP结果的支持度计数误差小于SmartTrunc,这与理论分析相符.

由图3可知,隐私保护预算s越大,F-score越大,即隐私算法挖掘结果的噪声频繁项集的可用性越高.DFDP中的F-score明显大于SmartTrunc中的F-score,即DFDP结果的可用性高于SmartTrunc,同样与理论分析相符.

5 结束语

本文针对SmartTrunc算法存在的不足,提出了一种改进的DFDP算法.DFDP无传播误差,全局敏感度更小,不需截断长事务记录,适用范围更广.理论分析与实验结果均表明,改进的DFDP减小全局敏感度和提升可用性的方法是有效的,但DFDP所基于的候选项集可能很大.在确保算法优势的前提下,如何缩减候选项集以提升DFDP的时空效率有待进一步深入研究.

[1] SWEENEY L.k-anonymity:a model for protecting privacy[J]. International J Uncertainty Fuzziness and Knowledge based Systems,2002,10(5):557-570.

[2] 谭瑛. 数据挖掘中匿名化隐私保护研究发展[J]. 科技导报,2013(1):75-79.

[3] DWORK C. Differential privacy[C]//Proceedings of the 33rd International Colloquium on Automata Languages and Programming (ICALP06). Berlin:Springer,2006:1-12.

[4] BHASKAR R, LAXMAN S, SIMTH A, et al. Discovering frequent patterns in sensitive data[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery Data Mining,2010:503-512.

[5] LI N, QARDAJI W, SU D, et al. Privbasis:frequent itemset mining with differential privacy[C]//Proceedings of the 38th Conference of Very Large Database,2012:1340-1351.

[6] 张啸剑,王淼,孟小峰. 差分隐私下一种精确挖掘top-k频繁模式方法[J]. 计算机研究与发展,2014,51(1):104-114.

[7] CHEN R, MOHAMMED N, FUNG B C M, et al. Publishing set-valued data via differential privacy [C]//Proceedings of the 37th Conference of Very Large Databases,2011:1087-1098.

[8] ZENG C, NAUGHTON J, CAI J Y. On differential private frequent itemsets mining[J]. Proceedings of the PVLDB Endowment,2012,6(1):25-36.

[9] 方开泰,许建论. 统计分析[M]. 北京:科学出版社,1987.

[10] DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[C]//Proceedings of the 3rd Conference on Theory of Cryptography Conference(TCC06). Berlin:Springer-Verlag,2006:265-284.

[11] MCSHERRY F. Privacy integrated queries:An extensible platform for privacy-preserving data analysis[C]//Proceedings of the ACM SIGMOD International Conference on Management of data (SIGMOD),2009:19-30

[12] AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules[C]//Proceedings of the 1994 International Conference on Very Large Data Bases (VLDB’94),1994:487-499.

[13] MONREALE A, PEDRESCHI D, PENSA R G, et al. Anonymity preserving sequential pattern mining[J]. Artificial Intelligence and Law,2014,22(2):141-173.

(编辑 余 毅)

An Algorithm for Mining Frequent Itemset Based on Differential Privacy Without Propagation Error

LIAO Yong, FENG Shan

(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Protection based on differential privacy method has nothing to do with the background knowledge related about the protection model and can be used to resist arbitrary form of attacks in data mining. For algorithm SmartTrunc based on idea of differential privacy protection with interference, its disadvantages are as following: The 1st is that usability of mining results will be reduced for the reason of propagation error. The 2nd is that global sensitivity will be increased very large and it will lead great expectation value used in noise disturbing. In order to eliminate the propagation error thoroughly, a new algorithm DFDP utilizes true frequentk-itemsets to generate candidatek+1-itemsets but not disturbed frequentk-itemsets like SmartTrunc. Meanwhile, to decrease the noise amount needed in interfering, a new mapping function is used to decrease the global sensitivity to 1. Theoretical analysis and experimental results show that the usability of the mining result can be effectively improved and the noise amount needed to assure the data mining protection can be obviously smaller with the algorithm DFDP.

frequent itemset; privacy preserving; differential privacy; Laplace disturbance; propagation error

2016-04-10

四川省教育厅自然科学重点基金(15ZB0029)

TP311

A

1001-8395(2017)01-0127-06

10.3969/j.issn.1001-8395.2017.01.021

*通信作者简介:冯 山(1967—),男,教授,主要从事智能软件平台开发和数据挖掘的研究,E-mail:fengshanrq@sohu.com