关于ZP-凝聚环

徐龙玉, 胡 葵, 万吉湘, 王芳贵

( 1. 西南科技大学 理学院, 四川 绵阳 621010; 2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621000;

关于ZP-凝聚环

徐龙玉1, 胡 葵1, 万吉湘2, 王芳贵3

( 1. 西南科技大学 理学院, 四川 绵阳 621010; 2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621000;

3. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

给出ZP-凝聚环的概念,举例说明左ZP-凝聚环不一定是右ZP-凝聚环,并利用ZP-内射盖及ZP-平坦预包对ZP-凝聚环进行一系列的等价刻画,如R是左ZP-凝聚环,当且仅当 ZP-平坦右R-模的直积是ZP-平坦右R-模,当且仅当任意右R-模有一个ZP-平坦预包.证明左 ZP-凝聚环上的任意左R-模存在 ZP-内射盖,并揭示若R是左ZP-凝聚环,则RR是ZP-内射模,当且仅当任意左R-模有一个满的ZP-内射盖,当且仅当任意右R-模有一个单的ZP-平坦预包.

ZP-凝聚环; ZP-内射模; ZP-平坦模; ZP-内射盖; ZP-平坦预包

1 预备知识

本文所有的环都是带有单位元1的结合环,所有的模都是酉模.令M为左R-模以及X为M的一个子集.对任意x∈X,记lR(X)={r∈R:rx=0}为X在R中的左零化子.若Y是R的一个子集,Y在M中的右零化子用rM(Y)表示.特别地,对于a∈R,r(a)与l(a)分别表示a的右零化子和左零化子.对于任意m∈M,若l(m)是RR的本质理想,则称m是奇异元.M中所有奇异元的集合用Z(RM)表示[1].特别地,R的左(右)奇异理想用Z(RR)(Z(RR))表示,为R的双边理想.称环R为右非奇异环,若Z(RR)=0.反之,称环R为右奇异环,若Z(RR)=R[2].R-模M的特征模M+定义为M+=HomZ(M,Q/Z).左R-模M的对偶模M*=HomR(M,R)是右R-模.

左R-模M是有限表现的,若存在一个正合列0→K→F→M→0,其中F是有限生成自由模且K是有限生成模.左R-模M是凝聚模[2],若M的每个有限生成子模是有限表现的.R是左凝聚环，若RR是一个凝聚模.凝聚环的性质以及推广得到了广泛的关注[3-13].本文将凝聚环中的有限生成理想限定到环的奇异理想中的主理想,提出了ZP-凝聚环的概念,并利用包和盖对该环进行系列的等价刻画.

首先介绍包与盖的定义.

定义 1[14]令C为R-模类.对于R-模M,C∈C,模同态f:C→M称为M的C-盖[14],若以下条件成立:

1) 对任意同态h:C′→M,其中C′∈C,存在一个同态g:C′→C,使得h=fg;

2) 若g是C的自同态,其中f=fg,则g一定是自同构.

若1)成立,但2)不一定成立,f:C→M称为C-预盖.对偶地,有C-(预)包的定义.一般情况下,C-盖和C-包不一定成立,但若成立,在同构的意义下是惟一的.

2 主要定理及证明

定义 2.1 称环R为左ZP-凝聚环,若对于任意a∈Z(RR),Ra是有限表现左R-模.相应地,可定义右ZP-凝聚环,称环R是ZP-凝聚环,若R既是左ZP-凝聚环也是右ZP-凝聚环.

命题 2.2 对于环R,以下条件等价:

1) R是左ZP-凝聚环;

2) 对任意a∈Z(RR),l(a)是有限生成左R-模;

3) 对任意a∈Z(RR),(R/aR)*是有限生成左R-模.

证明 1)⟺2) 对任意a∈Z(RR),存在一个正合列0→l(a)→R→Ra→0;因此Ra有限表现当且仅当l(a)是有限生成左R-模.

2)⟺3) 由文献[15]知(R/aR)*≅l(a).

凝聚环显然是ZP-凝聚环,然而ZP-凝聚环不一定是凝聚环.

例 2.3 1) 右非奇异环是右ZP-凝聚环;

2) 显然,整环是ZP-凝聚环,但整环不一定是凝聚环;

3) 令R为非凝聚交换整环且G是一个自由交换群,其中rankG=∞.群环RG不是凝聚环,但是RG是一个半本原整环,因此是ZP-凝聚环.

例2.4说明了左ZP-凝聚环不一定是右ZP-凝聚环.

例 2.4 令域K的子域L使得dimLK=∞,且存在一个域同构f:K→L(例如,L=Q(x2,x3,…,xn),K=Q(x1,x2,x3,…,xn)).令R=K×K且乘法为

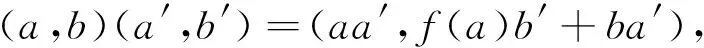
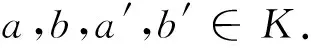
由以上法则知R有3个右理想,(0),R,及(0,K)=(0,1)R,易验证(0,K)也是一个左理想.Z(RR)以及Z(RR)是环R的双边理想,由其性质知Z(RR)=Z(RR)=(0,K).现令a=(0,1),则r(a)=(0,K),故(0,K)是一个有限表现右R-模;因此R是一个右ZP-凝聚环.另一方面,a∈Z(RR)且l(a)=(0,K),而(0,K)不是有限生成左R-模[3];因此由命题2.2知R不是左ZP-凝聚环.

为了在刻画ZP-凝聚环时便于描述,此处介绍ZP-平坦模与ZP-内射模的定义.

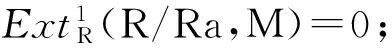
注 2.6 显然,P-内射左R-模是ZP-内射的;P-平坦右R-模是ZP-平坦的,但反之不一定成立.如令R是整环但不是域,则Z(RR)=Z(RR)=0且RR不是可除的.由文献[2]知,RM是P-内射模当且仅当RM是可除模;因此RR是ZP-内射模但不是P-内射模.现取非零非单位元a∈R,则R/aR是ZP-平坦模但不是P-平坦模.

命题 2.7ZP-平坦右R-模的纯子模是ZP-平坦右R-模.

故(N1)+是ZP-内射左R-模.同理可知N1是ZP-平坦右R-模.

定理 2.8 对于环R,以下条件等价:

1) R是左ZP-凝聚环;

2)ZP-平坦右R-模的直积是ZP-平坦模;

3) RR的任意直积是ZP-平坦模;

4) (ZP-)内射左R-模的正向极限是ZP-内射模;

5) 左R-模M是ZP-内射模当且仅当M+是ZP-平坦模;

6) 左R-模M是ZP-内射模当且仅当M++是ZP-内射模;

7) 右R-模N是ZP-平坦模当且仅当N++是ZP-平坦模;

8) 任意右R-模有一个ZP-平坦预包;

9) 对任意a∈Z(RR),l(a)是有限生成左理想;

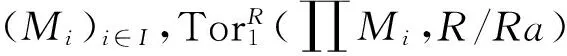
证明 1)⟹2) 令(Ni)i∈I是ZP-平坦右R-模集.由R是左ZP-凝聚环知,对任意a∈Z(RR),Ra是有限表现左R-模,故存在如图1的行为正合列的交换.

(∏Ni)Raf→(∏Ni)Rα↓β↓0→∏[NiRa]g→∏[NiR]

图 1

故由文献[2]及图1知α及β同构,则f是单同态.

2)⟹3) 显然.

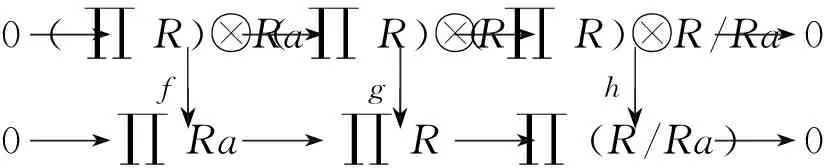
0→(∏R)Ra→(∏R)R→(∏R)R/Ra→0f↓g↓h↓0→∏Ra→∏R→∏(R/Ra)→0

图 2

既然R/Ra是有限表现左R-模,由文献[2]及图2知g和h同构,故由五引理知f同构,且由文献[2]知Ra是有限表现左R-模,故R是左ZP-凝聚环.

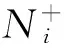
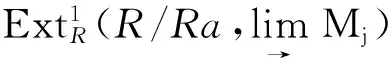
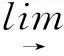
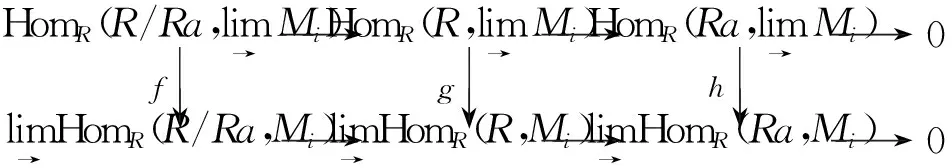
HomR(R/Ra,lim→Mi)→HomR(R,lim→Mi)→HomR(Ra,lim→Mi)→0f↓g↓h↓lim→HomR(R/Ra,Mi)→lim→HomR(R,Mi)→lim→HomR(Ra,Mi)→0

图 3

由文献[7]及图3知f和g同构,故由五引理知h同构.由文献[7]知Ra是有限表现左R-模,故R是左ZP-凝聚环.

8)⟹2) 可直接由文献[18]得.

1)⟺9) 由命题2.2可得.

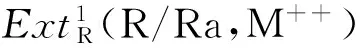
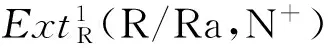
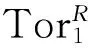
1)⟹10) 由文献[5]可知.

10)⟹3) 显然.

推论 2.9 若R为左ZP-凝聚环,则任意左R-模存在ZP-内射盖.

证明 令0→A→B→C→0左R-模的纯正合列,其中B是ZP-内射模,则0→C+→B+→A+→0分裂.由定理2.8知,B+是ZP-平坦模,则C+是ZP-平坦模,C是ZP-内射模;因此ZP-内射左R-模类在纯商模下是封闭的,故由文献[19]知任意左R-模有ZP-内射盖.

推论 2.10 令R为左ZP-凝聚环.以下条件等价:

1) 任意ZP-平坦右R-模是平坦模;

2) 任意ZP-内射左R-模是FP-内射模;

3) 任意ZP-内射且为纯内射左R-模是内射模.

此种情况下,R是左凝聚环.

证明 1)⟹2) 令M为任意ZP-内射左R-模.由定理2.8知,M+是ZP-平坦模,故由1)知M+是平坦模;因此M++是FP-内射模.既然M是M++的纯子模,则M是FP-内射模.

2)⟹3) 显然.

此种情况下,由定理2.8知,FP-内射左R-模的任意正向极限是FP-内射模,故由文献[6]知R是左凝聚环.

现在考虑什么条件下任意左R-模有一个满ZP-内射盖以及任意右R-模有一个ZP-平坦预包.

命题 2.11 令R为左ZP-凝聚环,以下条件等价:

1)RR是ZP-内射模;

2) 任意左R-模有一个满的ZP-内射盖;

3) 任意右R-模有一个单的ZP-平坦预包;

4) 任意内射右R-模是ZP-平坦模;

5) 任意平坦左R-模是ZP-内射模.

证明 1)⟹2) 令M为任意左R-模.由推论2.9知,M有一个ZP-内射盖f:C→M.另一方面,存在一个满同态g:R(I)→M.由于RR是左ZP-内射模,故由命题2.7的证明过程知,R(I)是左ZP-内射左R-模;因此存在同态h:R(I)→C使得g=fh.既然g是满同态,故f满同态.

2)⟹1) 令f:RM→RR是满的ZP-内射盖,则RR同构于M的一个直和加项,故由命题2.7的证明过程知,RR是ZP-内射左R-模.

3)⟹4) 令E是内射右R-模,则由3)知E能嵌入ZP-平坦右R-模.由定理2.8中7)⟹2)的证明可知,ZP-平坦右R-模的直和加项也是ZP-平坦右R-模,故E是ZP-平坦右R-模.

4)⟹5) 令M为任意平坦左R-模,则M+是内射模,由4)知M+是ZP-平坦R-模,因此由定理2.8知M是ZP-内射左R-模.

5)⟹1) 显然.

以下定理给出了交换ZP-凝聚环的等价刻画.

定理 2.12 对于交换环R,以下条件等价:

1)R是ZP-凝聚环;

2) 对任意ZP-内射R-模M及内射R-模N,同态模HomR(M,N)是ZP-平坦模;

3) 对任意内射R-模N,同态模HomR(R+,N)是ZP-平坦模.

证明 1)⟹2) 对任意ZP-内射R-模M及内射R-模N,既然Q/Z是内射余生成子,则存在正合列0→N→∏(Q/Z).因为N是内射模,则存在某一R-模C,使得∏(Q/Z)≅N⊕C,HomR(M,∏(Q/Z))≅HomR(M,N⊕C)≅HomR(M,N)⊕HomR(M,C).另一方面,HomR(M,∏(Q/Z))≅∏HomR(M,Q/Z)=∏M+,则HomR(M,N)是∏M+的直和加项.既然M是ZP-内射R-模,由定理2.8知∏M+是ZP-平坦模.由定理2.8中7)⟹2)的证明中可知ZP-平坦模的直和加项也是ZP-平坦模,HomR(M,N)是ZP-平坦模.

2)⟹3) 由R+是(ZP)-内射模.

3)⟹1) 注意到∏R++≅∏HomR(R+⊗R,Q/Z)≅∏HomR(R+,R+)≅HomR(R+,∏R+).既然R是R++的纯子模,则由文献[17]知∏R是∏R++纯子模.由3)知∏R++是ZP-平坦模.由命题2.7知∏R是ZP-平坦模,因此由定理2.8 知R是ZP-凝聚环.

[1] FUELBERTH J D, TEPLY M L. The singular submodule of a finitely generated module splits off[J]. Pacific J Math,1972,40(1):73-82.

[2] LAM T Y. Lectures on modules and rings[C]//Graduate Texts in Mathematics,189. New York:Springer-Verlag,1999:134.

[3] DING N Q, LI Y L, MAO L X. J-coherent rings[J]. J Algebra Appl,2009,8(2):139-155.

[4] DING N Q, CHEN J L. Coherent rings with finite self-FP-injective dimension[J]. Commun Algebra,1996,24(9):2963-2980.

[5] CHEN J L, DING N Q. Onn-coherent rings[J]. Commun Algebra,1996,24(10):3211-3216.

[6] STENSTROM B. Coherent rings and FP-injective modules[J]. J London Math Soc,1970,2(2):323-329.

[7] JONES M F. Coherence relative to a hereditary torsion theory[J]. Commun Algebra,1982,10(7):719-739.

[8] 徐龙玉,万吉湘,王芳贵. 关于ZP-内射维数及ZP-平坦维数[J]. 江西师范大学学报(自然科学版),2016,40(2):1-4.

[9] 王芳贵,汪明义,杨立英. 交换环上的极大性内射模[J]. 四川师范大学学报(自然科学版),2010,33(1):1-9.

[10] 陈勇,何承源.r-置换因子循环线性系统求解的快速算法[J]. 重庆师范大学学报(自然科学版),2010,27(5):37-41.

[11] 徐龙玉,汪明义. 关于零化子凝聚环[J]. 四川师范大学学报(自然科学版),2006,29(2):161-165.

[12] 徐龙玉,胡葵,乔磊,等. 非奇异环的同调刻画[J]. 四川师范大学学报(自然科学版),2016,39(4):514-517.

[13] 尹华玉,陈幼华. 整环上的w-凝聚性[J]. 四川师范大学学报(自然科学版),2016,39(5):639-642.

[14] ENOCHS E E, JENDA O M G. Relative homological algebra[J]. Trans Am Math Soc,1956,82(1):67-114.

[15] KATO T. Duality of cyclic modules[J]. Tohoku Math J,1967,19(3):349-356.

[16] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006:78.

[17] CHEATHAM T J, STONE D R. Flat and projective character modules[J]. Proc Am Math Soc,1981,81(2):175-177.

[18] CHEN J L, DING N Q. A note on existence of envelopes and covers[J]. Bull Austral Math Soc,1996,54(1):383-390.

[19] HOLM H, JΦGENSEN P. Covers, preenvelopes and purity[J]. Illinois J Math,2008,52(2):691-703.

2010 MSC：13C10; 13D99; 16D40

(编辑 郑月蓉)

On ZP-coherent Rings

XU Longyu1, HU Kui1, WAN Jixiang2, WANG Fanggui3

( 1.CollegeofScience,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan;2.CollegeofMathematicsandComputerScience,MianyangNormalUniversity,Mianyang621010,Sichuan;3.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

In this paper, the notion of the ZP-coherent ring is defined. An example is given to reveal that left ZP-coherent rings are not necessarily right ZP-coherent rings. The cover of ZP-injective modules and the envelope of ZP-flat modules are used to characterize ZP-coherent rings. It is proved that the ringRis left ZP-coherent if and only if any direct product of ZP-flat rightR-modules is ZP-flat if and only if any rightR-module has a ZP-flat preenvelope. In light of these facts, it is shown that every leftR-module over a left ZP-coherent ring has a ZP-injective cover. IfRis a left ZP-coherent ring, thenRRis ZP-injective if and only if every leftR-module has an epimorphic ZP-injective cover if and only if every rightR-module has a monomorphic ZP-flat preenvelope.

ZP-coherent rings; ZP-injective modules; ZP-flat modules; ZP-injective cover; ZP-flat prenvelope

2015-08-03

国家自然科学基金(11171240)

徐龙玉(1979—),女,讲师,主要从事环与模范畴理论的研究,E-mail:xulongyu3@163.com

O153.3; O154

A

1001-8395(2017)01-0068-05

10.3969/j.issn.1001-8395.2017.01.011