从混合模空间到加权Zygmund空间的积分算子的有界性和紧性
周 林
(连云港开放大学学工处,江苏连云港222006)
文献[1]中讨论了单位圆盘上从混合模空间到加权型空间的积分算子的有界性与紧性,文献[2]中讨论了单位球上从Zygmund空间到Bloch型空间的积分算子的有界性与紧性,文献[3]中讨论了单位球上Bloch型空间上积分算子的有界性与紧性,文献[4]中讨论了单位圆盘上有界解析函数空间与Bloch空间到Zygmund空间积分算子的有界性与紧性,文献[5]中讨论了单位圆盘上混合模空间到Bloch型空间的积分算子有界性与紧性.文献[6]中讨论了单位圆盘上混合模空间到Zygmund空间的加权微分复合算子的有界性与紧性,与文献[6]不同,文中讨论了混合模空间到Zygmund空间的积分算子的有界性与紧性.文中将要讨论的算子定义如下.文中字母C是一个正常数,不同的地方可以不同.
1 预备知识
H(D)表示D上所有的解析函数的集合.对于0<p,q<∞,φ为正规函数,若f∈H(D)且:

引理 1[6]设 0<p,q<∞,φ 是正规函数,f∈H(p,q,φ),那么对于任意自然数 n,存在一个与 f无关的正常数C,使得:

由M ont el定理及紧算子定义,可以得出下面的引理.
引理2设,u∈H(D),φ是D上的解析自映射,0<p,q<∞,φ是正规函数,则算子是紧算子的充要条件是是有界算子且对于H(p,q,φ)中在D的紧子集上一致收敛于0的任意有界列
2 主要定理及证明
定理1设0<p,q<∞,φ是正规函数,u∈H(D),φ是D上的解析自映射,则算子Cn,uφ:H(p,q,φ)→Z是有界算子的充要条件为:

证首先假设(1),(2)成立,那么对于任意f∈H(p,q,φ),由引理1可得:



由上式两式以及(3),(4)可知(1),(2)成立.
证毕.
定理2设0<p,q<∞,φ是正规函数,u∈H(D),φ是D上的解析自映射,则算子是紧算子的充要条件为是有界算子且:

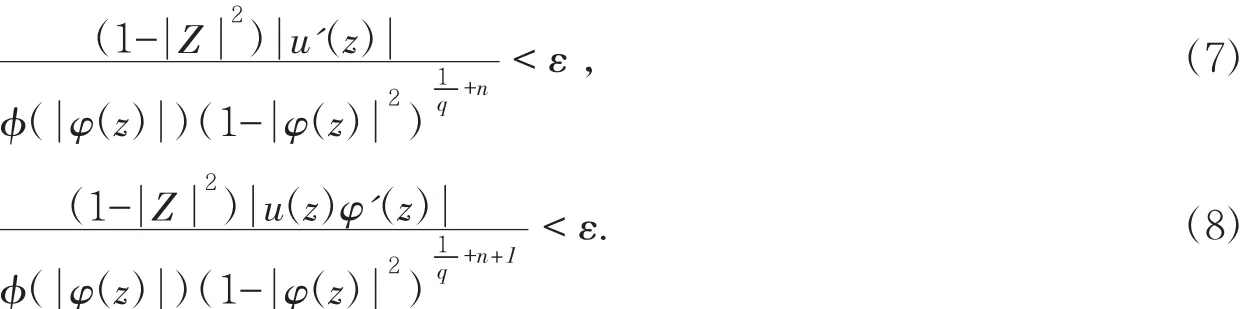

由(7)~(10)可知当 i>i0时,有:
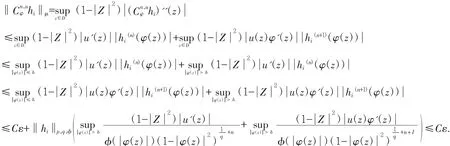

在以上两式两边令i→∞,可得:
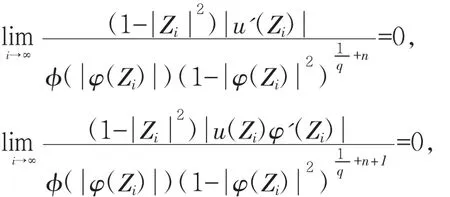
故(5),(6)成立.
证毕.
[1]Stevic'S.Generalized composition operators between mixed-norm and weighted-type spaces[J].Numerical Functional Analysis and Optimization,2008,29(7-8):959-978.
[2]Stevic'S.On an integral operator from the Zygmund space to the Bloch-type space on the unit ball[J].Bull Science Mathematics,2010,134(4):329-339.
[3]Stevic'S.On an integral operator between Bloch-type spaces on the unit ball[J].Glasg Mathematics,2009,51(2):275-287.
[4]LI Songxiao,Stevic'S.Products of Volterra type operator and composition operator from and Bloch spaces to Zygmund spaces[J].Journal of Mathematics Analysis and Application,2008,345:40-52.
[5]曹成堂,黄兴华.从混合模空间到加权Bloch空间的积分算子的有界性与紧性[J].淮海工学院学报(自然科学版),2012,21(1):11-14.
[6]LIU Yongmin,YU Yanyan.Weighted differentiation composition Operators from mixed-norm spaces to Zygmund spaces[J].Numerical Functional Analysis and Optimization,2010,31(8):936-954.
[7]Abdul Quddus,Al-Hadhrami LM.The product of differentiation and multiplication operator from the mixed-norm to the Bloch-type space[J].Acta Mathematics Science,2012,32A(1):68-79.

