在一般加权Bergman空间上的广义Volterra型算子①
罗庆仙
(广东茂名幼儿师范专科学校 理学院, 广东 茂名 525200)
1 相关研究
令Δ是复平面上的单位开圆盘,在Δ上的所有全纯函数组成的集合记为H(Δ).


当φ∈H(Δ)且φ(Δ)⊂Δ时,复合算子Cφ的定义为
(Cφf)(z)=f(φ(z)),z∈Δ,f∈H(Δ),
而加权复合算子Wφ,φ的定义为
(Wφ,φf)(z)=φ(z)f(φ(z)),z∈Δ,f∈H(Δ).
对于任意g∈H(Δ),定义Volterra型算子Tg如下:
与Tg密切相关的另一个算子,其定义为
很多学者对Volterra型算子的研究充满了兴趣。近几年来,林庆泽研究了加权shift算子加上Volterra型算子在Bergman空间上的不变子空间及约化子空间[2],并且给出了Volterra型算子在对数加权Banach空间之间的有界性和紧性的充要条件[3]。在参考文献[4]、[5]中,Lin等人分别刻画几个具体空间上Volterra型算子的有界性和紧性等。
广义Volterra型算子定义为下列四种形式:
广义Volterra型算子由Li等人首次提出,并且他们完善了该算子在一些具体空间上的性质[6-9]。自从该算子被提出来以后,很多学者不断去完善其性质,其中Ueki在参考文献[10]中研究了从加权Bergman空间到β-Zygmund空间的广义Volterra型算子的有界性和紧性,并且还给出其本性范数。而Mahyar和Rezaei则刻画了在QK空间上的广义Volterra型算子的有界性和紧性[11],更多的,Li和Ma[12]给出了广义Volterra型算子在Zygmund型空间到QK空间上的有界性和紧性的刻画。Sanatpour[13]中讨论了在Zygmund型空间上的广义Volterra型算子的本性范数,并且还推广到Bloch型空间等等。
不过到目前为止,作用在一般加权Bergman空间上的广义Volterra算子的有界性和紧性尚未刻画,从而,本文将给出其有界性和紧性的刻画。
2 定理的引入及其证明
接下来下文中的引理1和引理2分别给出了加权复合算子在一般的Bergman空间之间的有界性和紧性的刻画。
当ω是任意给定的正则权,p,γ>0是任意给定的实数时,对于z∈Δ,令


引理2设ω,μ是正则权,并且1 (3)对于足够大的γ′>0,有 为了刻画广义Volterra型算子在广义加权Bergman空间上的有界性和紧性,通过等价范数可以得到其有界性和紧性的充要条件。 定理1设ω,μ是正则权,g,φ∈H(Δ),φ(Δ)⊆Δ,(goφ)′⊆Δ,则: (2)当1 ③对于足够大的γ>0,则有 下面这个定理是刻画算子Tg,φ在Bergman空间之间的有界性和紧性,其证明和定理1是类似的。 定理2 设ω,μ是正则权,g,φ∈H(Δ),φ(Δ)⊆Δ,则: (2)当1 ③对于足够大的γ>0,有 定理3 设ω,μ是正则权,g,φ∈H(Δ),φ(Δ)⊆Δ,则: (2)当1 ③对于足够大的γ>0,有 定理4设ω,μ是正则权,g,φ∈H(Δ),φ(Δ)⊆Δ则: (2)当1 ③对于足够大的γ>0,有 本文利用一般加权Bergman空间上的加权复合算子的有界性、紧性和等价范数得到了一般加权Bergman空间之间广义Volterra型算子的有界性和紧性。这种证明方法简捷高效,为研究其它函数空间上的算子理论提供了一种新的思路。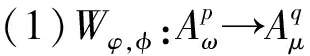
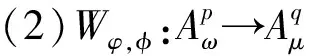
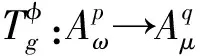

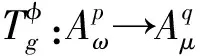
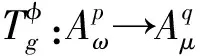
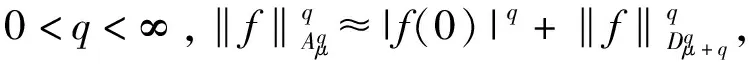

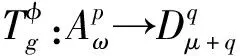
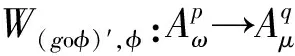
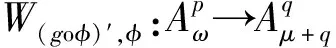
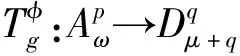
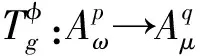
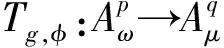
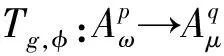
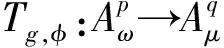
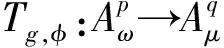
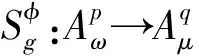
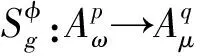
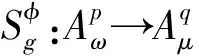
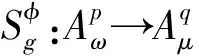
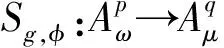
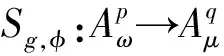
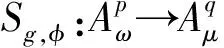
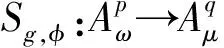
3 结语

