一类三循环半群的研究
徐文锋
(韶关学院数学与统计学院,广东韶关512005)
逆半群作为群最临近的推广,在半群理论中具有非常重要的作用.循环半群和双循环半群因其生成元简单,结构优美,一直以来对它们的研究都非常活跃,得到了许多很好的结论.文献[2-3]研究了双循环半群的同余刻画,文献[4-5]研究了广义双循环半群,文献[6]研究了一类特殊的三循环半群,文献[8]研究了4-循环半群的一个子半群,文献[7]研究了一类多循环半群.作为双循环半群的推广,本文研究了一类特殊的三循环半群.文中所用到的半群代数理论中的基本概念以及记号,如半群、循环半群、幂等元等,均与文献[1]相同,本文将直接引用而不再一一定义.
三循环半群根据其三个生成元之间关系的不同而得到不同的结构.例如,在文献[6]给出了三循环半群<p,的结构,在文献[7]研究了三循环半群的结构.本文所要研究的三循环半群定义如下本文讨论三循环半群 T 的元素结构,其中 N表示全体自然数集合.
1 三循环半群的元素结构
定理1 三循环半群T中的每一个元素都可以唯一的表示为aibjck,其中i,j,k∈N.
在证明定理1之前,先来讨论下面引理.
引理1 对于T中的元素a,b,c,有cia=abi,其中i∈N.
证 对i作数学归纳法.当i=0时有a=a,结论显然成立.假设结论对i时成立,那么i+1时,根据T的定义有ca=ab,因此有ci+1a=cica=ciab=abib=abi+1.证毕.
引理3 对于T中的元素b,c,若有j≥1,则有cibj=bi+j,其中i∈N.
证 对i作数学归纳法.当i=0时有bj=bj,结论显然成立.假设结论对i时成立,那么i+1时,根据T的定义有cb=b2,因此有证毕 .
引理 4 对于 T 中的元素 a,b,c,若有 j≥1,则有

由上述引理可证定理1.
2 三循环半群T的自然表示
双循环半群除了它的定义表示以外,还可以由集合N到N的映射构成的半群来表示,以及由自然数集上的二元序对构成的集合表示.最后一种表示法也是最常用的一种方法,称为双循环半群的自然表示.
三循环半群T的自然表示可以通过分析三循环半群T的运算,在集合N×N×N中定义乘法,使之成为一个与半群T同构的半群.
在研究三循环半群T的自然表示时,因其乘法运算法则比双循环半群乘法运算法则复杂许多,为了表述上方便,给出记号 N(x,y)定义为
定理2令N表示自然数集,在N×N×N上定义乘法。如下:

则(N×N×N,。)是一个半群,并且同构于三循环半群T.
证 对于T中任意两个元aibjck和albsct,根据结合律以及上一节的结论,分情况讨论如下:
(1)l=0.
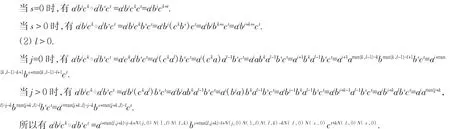
设 Π:T→(N×N×N,。)使得 aibjck→(i,j,k).根据以上计算,得到 Π 是同构映射.所以(N×N×N,。)是一个半群,并且同构于三循环半群T.
3 三循环半群T的幂等元
定理3 T的幂等元除1以外,都是具有形式aj+kbjck的元素,其中j,k∈N,j>0.

整理得:
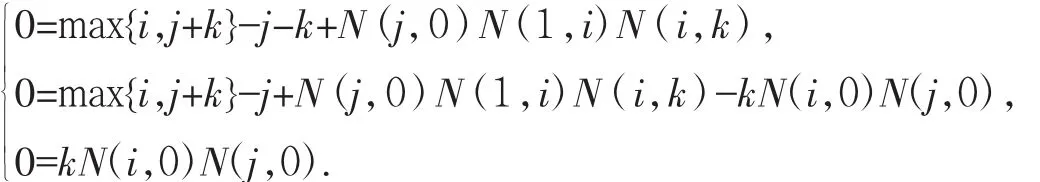
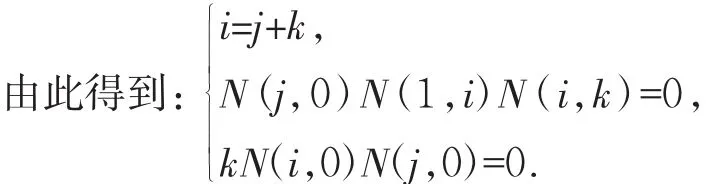
由上式得到i=j=k=0或者i=j+k,其中j,k∈N,j>0.于是得到T的幂等元除1以外,都是具有形式aj+kbjck的元素,其中 j,k∈N,j>0.
将T中的全体元素如下排列:

显然地,该排列从左到右可以分成无穷多个方块,其中第i个方块的全部元素构成集合{aibjck,j,k∈N},i=0,1,2,···从行上看,该排列第 j行的全部元素构成{aibjck,j,k∈N},j=1,2,···三循环半群 T 的幂等元分布如下:第0 个方块含有幂等元 1,第 i个方块具有幂等元 aibi,aibi-1c,···,aibci-1,共有 i个,其中 i≥1.
[1]ohn M H.Fundamentals of Semigroup Theory[M].Oxford:Oxford University Press,1995.
[2]周淑云.双循环半群同余的刻画[J].青海师专学报(教育科学版),2005,22(4):8-10.
[3]徐文锋.双循环半群上的同余结构[J].韶关学院学报(自然科学版),2012,33(8):11-13.
[4]蒋启芬,喻秉均.一类广义双循环半群[J].四川师范大学学报(自然科学版),1999,22(1):17-23.
[5]喻秉均,蒋启芬.广义双循环半群和Jones半群[J].数学进展,2000,29(3):235-244.
[6]朱用文.一类三循环半群[J].烟台大学学报(自然科学与工程),2006,19(3)166-169.
[7]江洪,田振际,王亚伟.一类多循环半群的研究[J].甘肃科学学报,2008,20(2):30-32.
[8]商宇,汪立民.关于4-循环半群的一个子半群-II[J].数学杂志,2013,33(6):983-988.

