带前馈补偿的弹标轨迹变论域模糊控制器设计

杜恩祥， 王双龙， 常 雷

(装甲兵工程学院兵器工程系， 北京 100072)

带前馈补偿的弹标轨迹变论域模糊控制器设计

杜恩祥， 王双龙， 常 雷

(装甲兵工程学院兵器工程系， 北京 100072)

为实现某车载导弹嵌入式模拟训练器的弹标运动轨迹精确控制，分析了将导弹控制指令转换为模拟训练器控制信号的方法，建立了控制对象数学模型，根据系统特点设计了弹标轨迹变论域模糊控制器，并使用前馈通路补偿主要扰动和固定装置结构设计上的不足。在MATLAB/Simulink环境下进行了建模与仿真，分析了其单位阶跃响应和正弦跟踪响应，并与经典控制方法进行了对比，结果表明：该控制器总体性能更优越，前馈回路准确有效。

变论域模糊控制； 弹标轨迹； 前馈补偿

某车载导弹嵌入式模拟训练器采用模拟弹标结合实际场景来实现，其模拟弹标组件固定安装于观瞄装置前方，通过光学成像模拟无限远的导弹光点，双轴步进电机控制系统根据车载发射控制系统指令作出响应，驱动弹标在俯仰和偏航方向按照相应的轨迹运行，达到仿真训练的目的。针对此类运动轨迹精确控制问题，经典控制理论的控制精度不能满足要求，容易超调，稳定性差，需要引入更先进的控制理论，其中一个主要的方向就是模糊控制[1]。相关领域学者已将神经网络、粒子群算法、双模控制、经典PID控制等方法与模糊控制进行了有机结合[2-9]，取得了较好的控制效果；但是这些研究极少考虑被控对象的时变特性以及主要干扰的处理。

为此，笔者根据弹标轨迹控制系统的特点，设计一种带前馈补偿的弹标轨迹变论域模糊控制器，在自适应率中加入时变分量；同时分析确定系统的主要扰动因素，使用前馈控制方法与反馈控制相结合，对主要干扰进行补偿。

1 弹标轨迹控制系统

弹标轨迹控制系统结构如图1所示，主要由控制器、驱动电机以及可被导弹测角仪识别、捕捉的模拟弹标等组成。

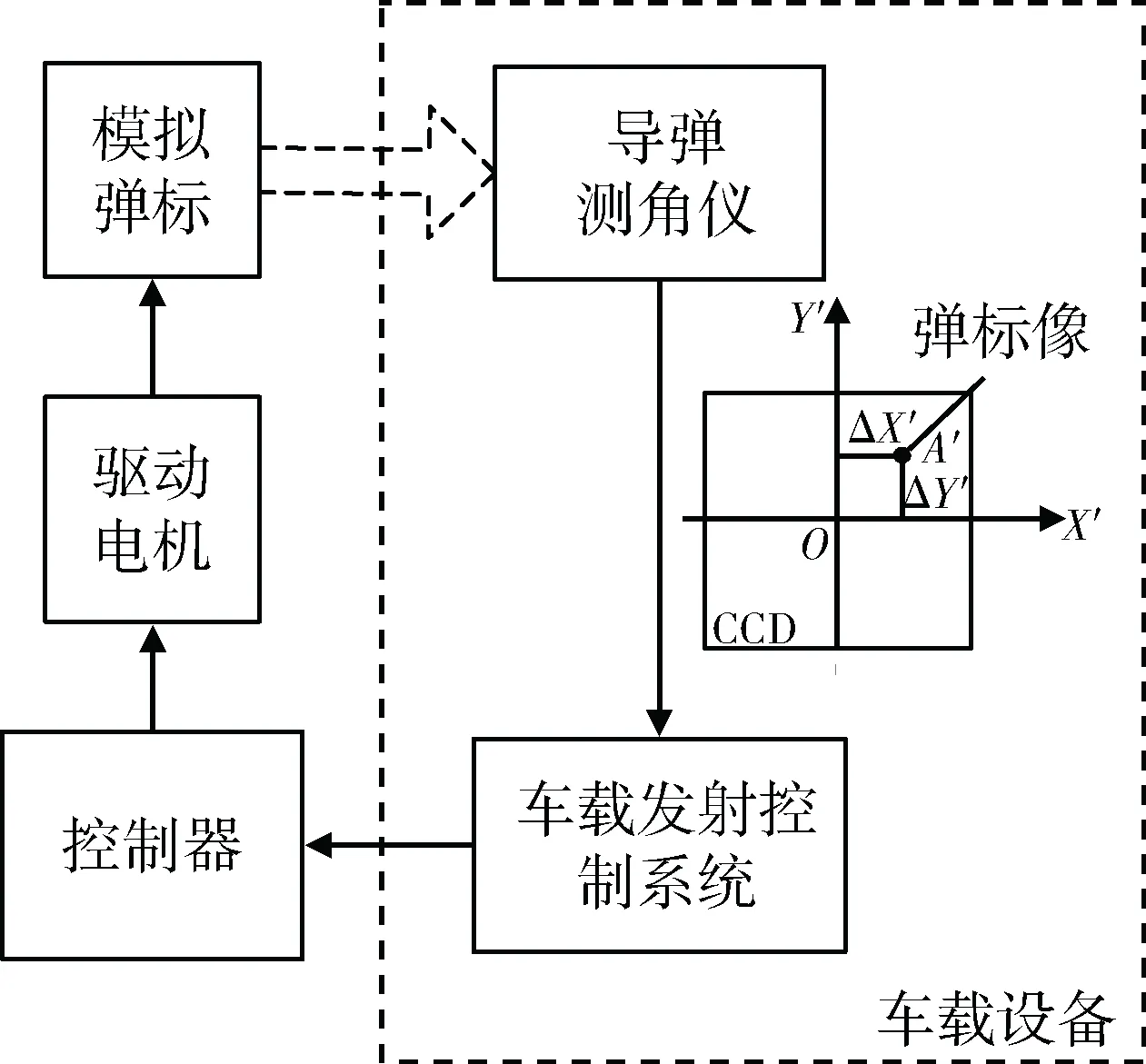
图1 弹标轨迹控制系统结构

弹标轨迹控制系统采用嵌入式设计，与车载设备共同组成闭环控制系统。导弹测角仪通过CCD摄像机采集模拟弹标的位置信息，产生偏差信号，经车载发射控制系统处理后得到导弹控制指令并输入控制器，控制驱动电机按照理想的转速和方向运行，驱动弹标在平面上模拟实弹的飞行轨迹。导弹测角仪不断测得角偏差，形成闭环控制，模拟某型导弹的发射过程和飞行轨迹，以达到训练目的。

2 控制器输入信号处理

2.1 占空比指令转化为归一化指令

嵌入式模拟训练器采用车载设备产生的每周期4次过零点的脉冲宽度调制信号，需要将旋转导弹的单通道控制信号转换为双轴步进电机控制信号，首先，要根据信号的相位从信号中提取出俯仰和偏航2个方向的指令系数。图2为控制导弹的脉冲宽度调制信号。

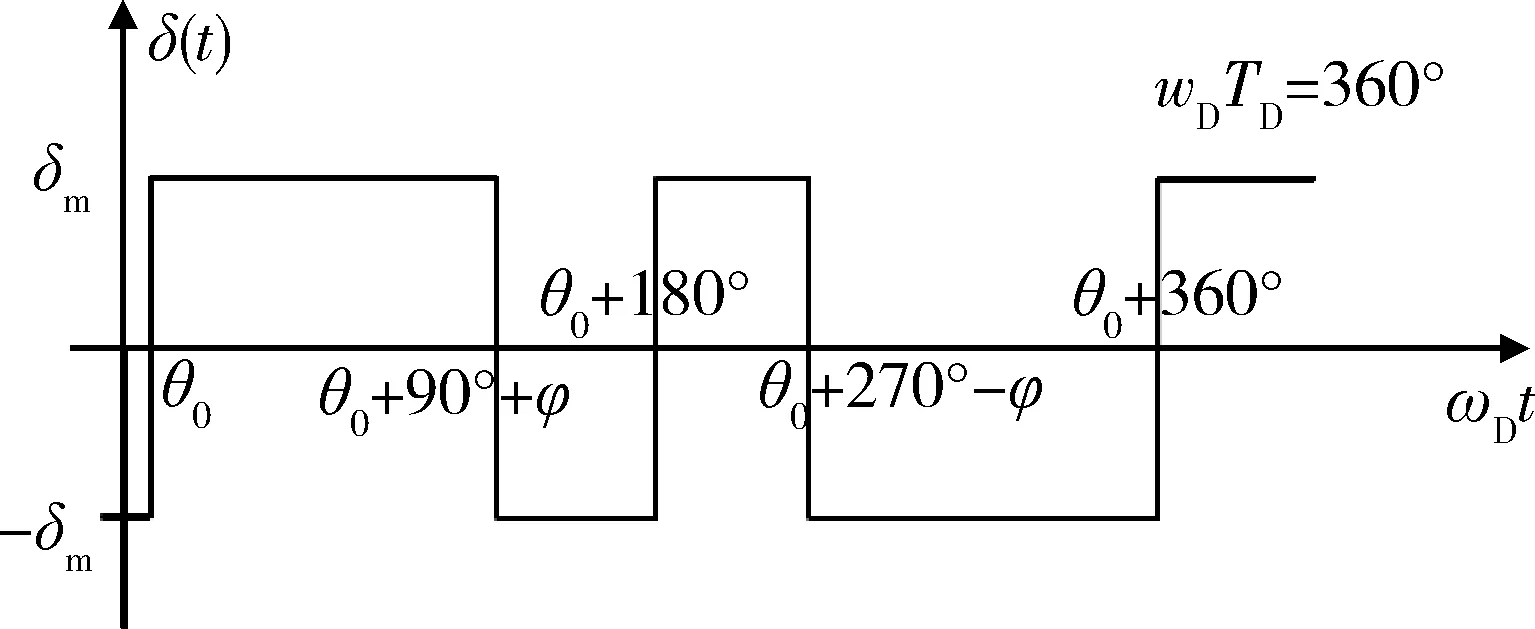
图2 控制导弹的脉冲宽度调制信号

根据旋转导弹的控制原理，控制信号δ(t)包含了俯仰和偏航方向的信息，幅值为δm；初始相位角θ0决定俯仰与偏航2部分向量和的方向，而调宽角φ则决定2部分向量和模的大小。δ(t)可表示为

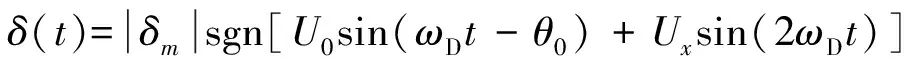
(1)

式中：U0、Ux为系数；ωD为旋转导弹角速度。

由于控制力的变化较为复杂，为便于计算，取每个周期的平均值，经转换作为该周期内步进电机的控制信号。根据指令系数的定义，有

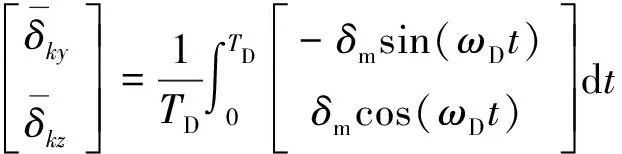
(2)

式中：TD为旋转导弹周期；

(3)

分别为俯仰、偏航方向的周期平均控制量，归一化之后得到俯仰、偏航方向的指令系数Ky、Kz，即

(4)

2.2 指令系数处理为步进电机脉冲信号

步进电机的驱动信号是正向脉冲方波序列，脉冲频率与步进电机的转速成正比。当指令系数达到最大时，步进电机应驱动弹标达到最快的移动速度；当指令系数为0时，弹标停止。因此，需要设计传递函数，生成频率与指令系数成一定比例的脉冲序列。俯仰、偏航方向的传递函数分别为

(5)

式中：a′为时间常系数；考虑到重力因素对模拟弹标的影响可以忽略不计，需要在俯仰方向的控制指令系数Ky中减去重力补偿分量K0，根据技术手册，常温下K0=0.48±0.03。

3 控制对象数学建模

在嵌入式模拟训练器中，用于控制弹标的驱动部分包括混合式步进电机、联轴器、丝杠、运动平台和焊件等。选用步进电机的步距角为1.8°，驱动器细分倍数为8，底座平台x轴滚珠丝杠螺距为1 mm，则可以计算x轴步进电机的脉冲当量。

弹标运动的力矩由2个坐标轴方向的步进电机共同作用生成，若要建立驱动部分数学模型，应首先分析步进电机。步进电机是依靠电脉冲信号驱动的电子元件，在正常工作范围内严格响应电脉冲信号，每接收一个脉冲信号，就转过一个固定的角度(步距角)，不受负载和输入电压波动的影响，具有良好的控制特性。考虑到步进电机的高度非线性和复杂特性，在实际计算中难以完全精确描述步进电机，因此，进行如下假设：1)只考虑电机单相励磁的情况，即任意时刻只有一相绕组通电；2)忽略各相之间的互感，只考虑电机绕组的自感；3)不计永磁体回路、电机气隙造成的漏磁。

对于步进电机第j相，其电压平衡方程为[2]

uj=Rij+Ldij/dt-Kmωsin(Nrθ)，

(6)

式中：uj和ij分别为第j相绕组的电压和电流；R为绕组电阻；L为绕组电感；Nr为转子齿数；Km为反电势系数；ω为电机角速度；θ为电机转角。

根据电机角速度定义，有

ω=dθ/dt。

(7)

由于只考虑电机单相励磁的情况，因此电机的转子力矩平衡方程可简化为[2]

Jdω/dt+Bω+TL=Kmijsin(Nrθ)，

(8)

式中：J为转动惯量；B为阻尼系数；TL为负载转矩。

联立式(6)-(8)即可得到电机运动方程，进行拉普拉斯变换，得到电机传递函数[7]：

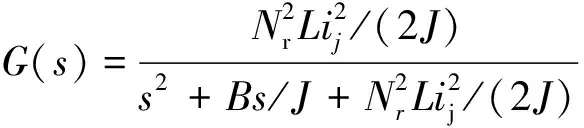
(9)

4 带前馈补偿的自适应模糊控制器

由于某车载导弹嵌入式模拟训练器包含了较多非线性、时变、不连续的控制环节，考虑到各种干扰以及步进电机运行的不连续性，若只依靠控制箱模块自带的参数固定的经典PID控制算法，难以达到理想的控制效果，需要控制系统适应具体工作环境，而且能实时整定出最优的控制参数。

模糊控制的优势在于不需要建立确切的系统模型，可以根据控制经验建立控制规则库；但模型建立后无法适应系统工作状态的变化，从而无法达到最优的控制效果。因此，需要加入带有自适应特性的改进模糊控制器。

嵌入式模拟训练器的弹标组件在偏航(水平)方向与炮塔观瞄设备刚性连接一起转动，在跟踪移动目标时，弹标运动与实际控制指令有较大误差，因此，在偏航方向采集观瞄跟踪装置的光电编码器信号作为前馈通路的输入，以补偿弹标的偏航方向位移量。带前馈补偿的自适应模糊控制器原理如图3所示。

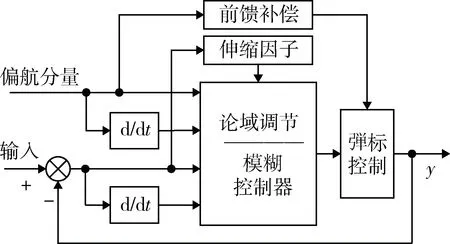
图3 带前馈补偿的自适应模糊控制器原理

4.1 自适应模糊控制器

4.1.1 输入、输出量论域

模糊控制器的输入量为设定值偏差e0和偏差变化率ce0，以及偏航分量e1和偏航分量变化率ce1，为了便于计算和实现，将其分别求和，得到总的偏差e和偏差变化率ce，作为模糊控制器的输入。

e和ce的模糊控制论域均确定为[-E,E]，量化等级均取为7个等级：{NB，NM，NS，0，PS，PM，PB}。输出量y的模糊控制论域确定为[-Y,Y]，其量化等级更精细，取为11个等级：{N5，N4，N3，N2，N1，0，P1，P2，P3，P4，P5}。

4.1.2 隶属度函数

为简化控制器结构，隶属度函数采用三角形函数，其中，偏差e和输出y的隶属度函数在论域中心区域分布更加密集，偏差变化率ce则均匀分布，其隶属度函数图像如图4所示。

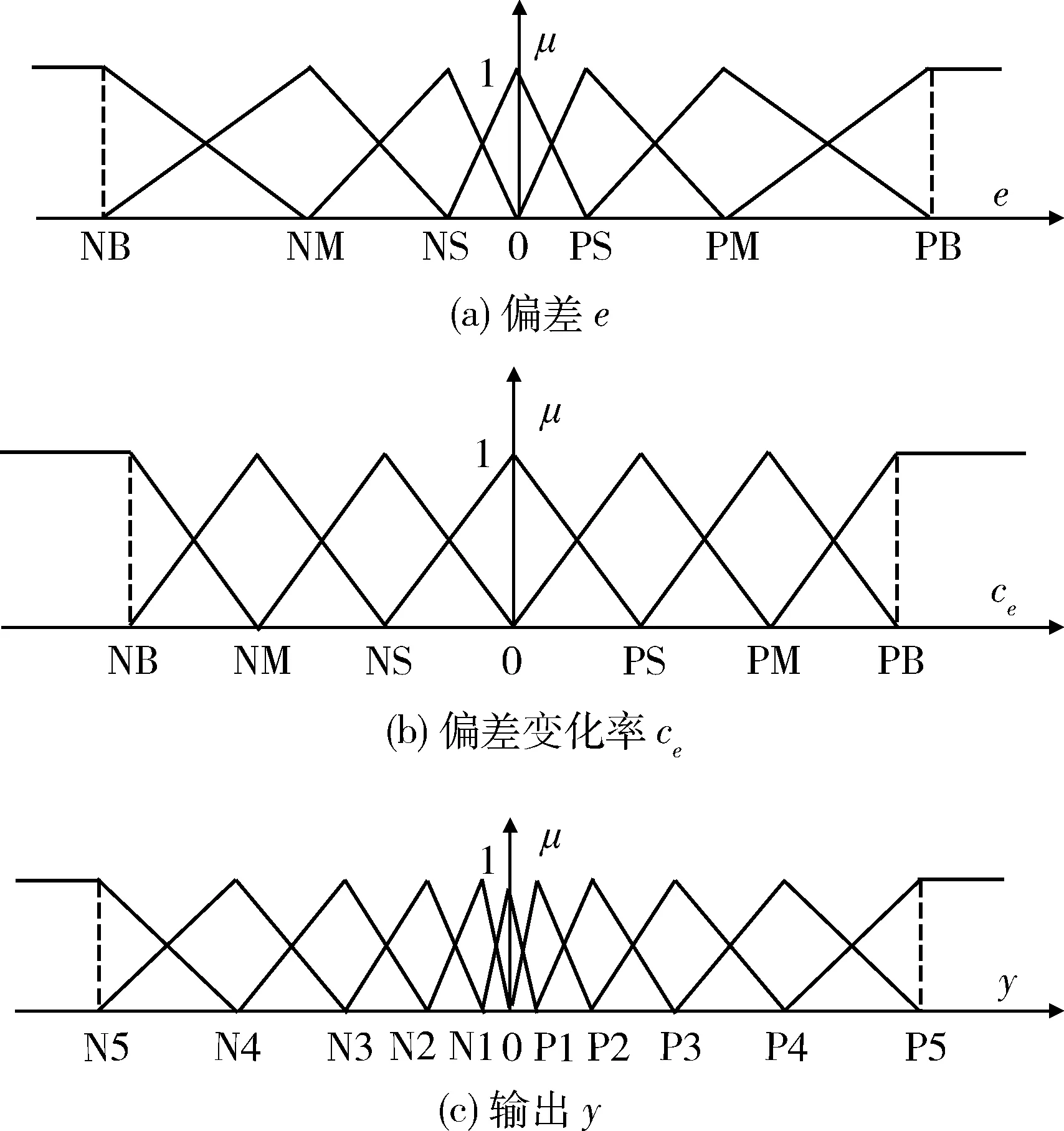
图4 隶属度函数图像

4.1.3 模糊控制规则

闭环控制的目的是消除偏差，模糊控制通过建立模糊规则库来实现，其推理准则在于位置偏差及其变化率的各种情形。如：给出一定大小和方向的控制量，当偏差很大且有正向变化趋势时，应给出负向最大控制量；若变化趋势负向变化，则应适当减小控制量，但方向不变。图5为模糊控制规则曲面。

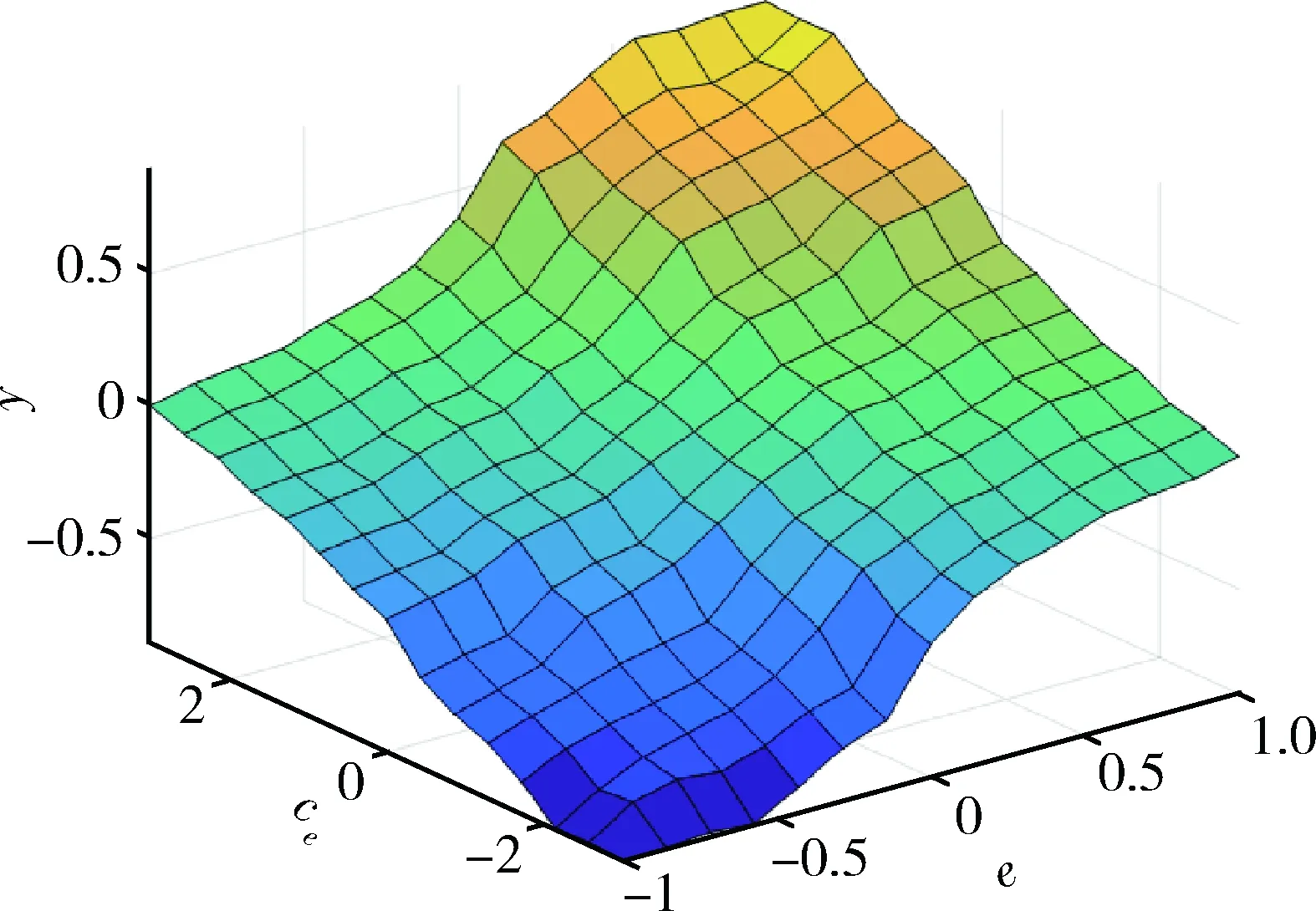
图5 模糊控制规则曲面

4.1.4 自适应率

模糊控制器的精度由输入、输出的量化等级确定，等级划分越精细，精度越高，但由于受硬件性能以及数据刷新率的要求限制，量化等级不可能过于精细，因此，可将隶属度函数偏差较小的中间部分设计得更密集。但更有效的方法是采用变论域模糊控制，根据偏差大小调整论域伸缩，即构建论域区间的伸缩因子，如：偏差e的伸缩因子为α(e)，其可变论域应为[-α(e)E，α(e)E]；偏差变化率ce的伸缩因子为α(ce)，其可变论域则为[-α(ce)E，α(ce)E]；输出量y的伸缩因子为β(y,t)，则其可变论域为[-β(y,t)Y，β(y,t)Y]。

此外，自适应率还应考虑系统的时变性，对弹标轨迹控制系统而言，其时变性体现在要模拟的实际系统的时变特性：角偏差信号在导弹发射后不同时刻(观测点与导弹距离)具有不同的实际意义，即在相同的角偏差下，观测点与导弹距离越远，导弹偏离瞄准线越多，但给导弹的控制力是不变的。角偏差与实际偏差的关系如图6所示。

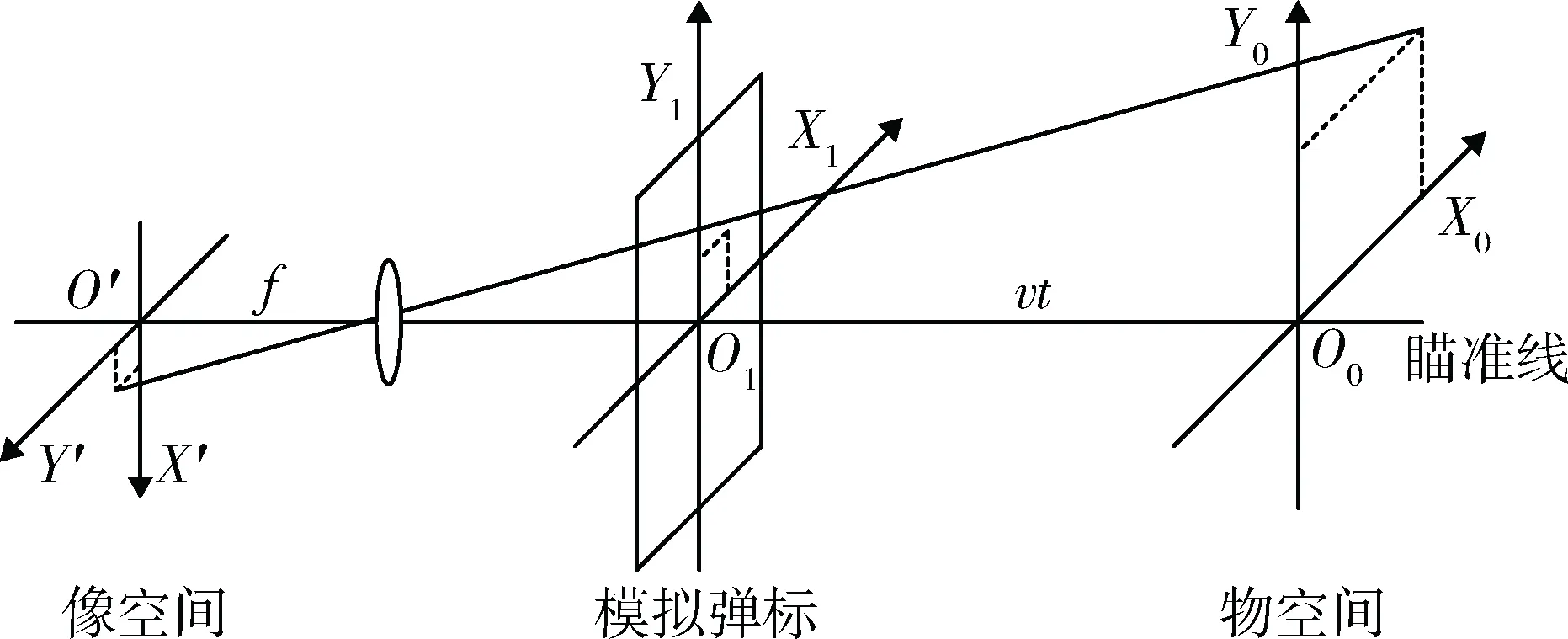
图6 角偏差与实际偏差的关系

若控制力不变，则单位时间内导弹在X1O1Y1平面实际位移量相同，但不同的时刻(观测点与导弹距离)反馈到观测点的角偏差变化量不同，即随着观测点与导弹距离的增加，控制效果变弱。像空间和物空间的弹标位移量Δe′和Δe0的关系为

Δe0/Δe′=[z(t)+a]/f(t)，

(10)

式中：f(t)为测角仪焦距变化函数；a为模拟弹标(导弹)到测角仪的距离；z(t)为导弹在瞄准线方向的位移函数。

由于在模拟训练时弹标并不沿瞄准线方向运动，因此像空间和模拟弹标位移量Δe′和Δe的关系为

Δe/Δe′=a/f(t)。

(11)

最后，得到模拟系统相对于实际情况的修正系数：

k=Δe/Δe0=a/[z(t)+a]。

(12)

输入、输出量的伸缩因子分别表示为

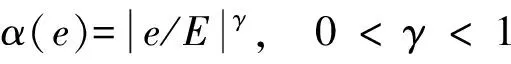
(13)

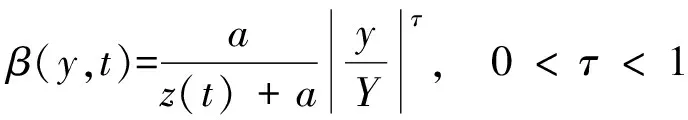
(14)

式中：γ、τ为调节参数。

通过导弹在重要位移点处的时间数据，可以拟合出导弹在瞄准线方向的位移函数：

(15)

由于α(e)采用常用的比例指数型伸缩因子，能够满足伸缩因子的定义性质，因此这里主要验证β(y,t)的性质：

1)对于任意y∈[-Y,Y]，β(y,t)=β(-y,t)，满足对偶性；

2)如果y=0，则β(0,t)=0，满足近零性；

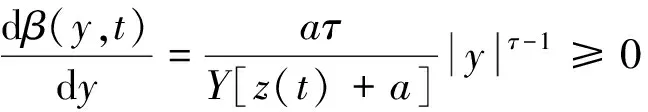
4)令y=±Y，有β(±Y,t)=a/[z(t)+a]，考虑导弹导引过程，y=±Y时导弹受控制力最大，在正常情况下，只有在发射初始时刻才有如此大的偏差，否则必然脱靶，因此此时t→0，由式(15)可知z(t)→0，所以β(±Y,t) →1，满足正规性；

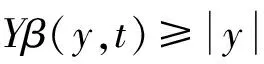
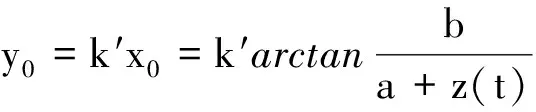
(16)

图7 恒定线偏差(垂直距离)下的角偏差

由于闭环控制特性，实际系统中y≤y0，则

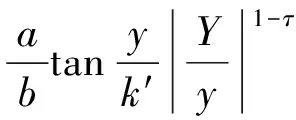
(17)

又τ∈(0,1)，若τ→0，且在x∈[0,+∞)区间上，有tanx≥x，则

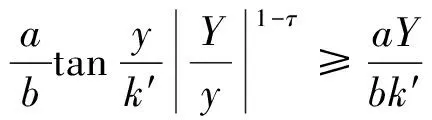
(18)

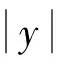
4.2 前馈控制补偿

对于闭环负反馈系统，控制器响应的是被控对象偏离设定值的偏差量，即被控对象被干扰产生不利影响之后，控制作用才能介入回路，调节被控量恢复设定值。在控制过程中，被控量是偏移给定值的，而且从开始调节到被控量变化也需要一段时间，滞后现象较明显。

对于已确定的某些干扰因素，前馈回路能够尽可能减少干扰对被控对象的影响，作为反馈控制的有力补充，提高系统快速跟踪性能。

在嵌入式模拟训练器中，导致偏差的一个典型的因素就是跟踪移动目标时瞄准线的变化量，当导弹跟踪装置做水平回转(或俯仰)运动时，系统将光电编码器输出的速度信号作为前馈回路的输入，在产生干扰时进行补偿。同时，调节控制器通路参数，以弥补模拟训练器结构设计的不足，即弹标组件在偏航(水平)方向与炮塔观瞄设备刚性连接，这与实际情况有较大差距。

前馈控制的设计采用模糊控制。由于控制器具体的传递函数D(s)难以确定，因此选用的前馈回路设计如图8所示。其中：r(s)为输入；N(s)为观测到的跟踪部分分量；DN(s)为前馈开环回路的传递函数；GN(s)可根据需要适当确定；G(s)为控制对象；y(s)为输出。

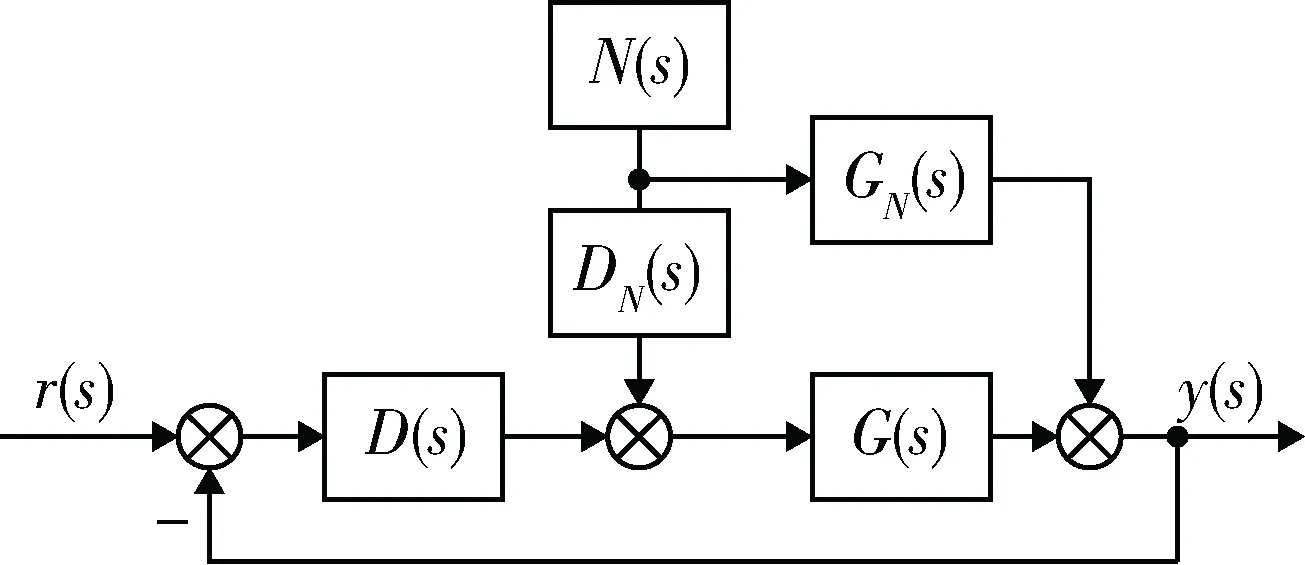
图8 前馈回路设计

考虑零输入，即r(s)=0，前馈通路传递函数为

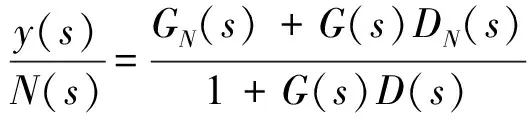
(19)

如果前馈控制能完全补偿扰动，则有y(s)=0，代入式(19)可得

GN(s)+G(s)DN(s)=0，

(20)

则有前馈通路传递函数：

DN(s)=-GN(s)/G(s)。

(21)

5 系统仿真及结果分析

为验证设计的前馈补偿变论域模糊控制器的有效性，在MATLAB的Simulink 组件中建立仿真模型，对弹标轨迹控制系统进行仿真。由于系统输入信号是归一化的指令，且正常情况下为平稳跟踪，偏航分量极小，因此e的基本论域确定为[-1,1]，ce是e的微分，物理意义为弹标速度，弹标最大速度为

Vm=nωm/(2π),

(22)

式中：n为驱动丝杆的螺距；ωm为电机最大角速度。

经计算，确定ce的基本论域为[-3,3]。步进电机仿真参数设置为：自感L=0.125 H，转动惯量J=0.005 kg·m2，转子齿数Nr=50，绕组电流i=0.6 A，阻尼系数B=0.000 2 N·m·s/rad 。

Simulink仿真模型如图9所示，经过反复对比实验，确定最优的控制参数：输入量的伸缩因子调节参数γe=0.1,γce=0.95；输出量的伸缩因子调节参数τ=0.01。

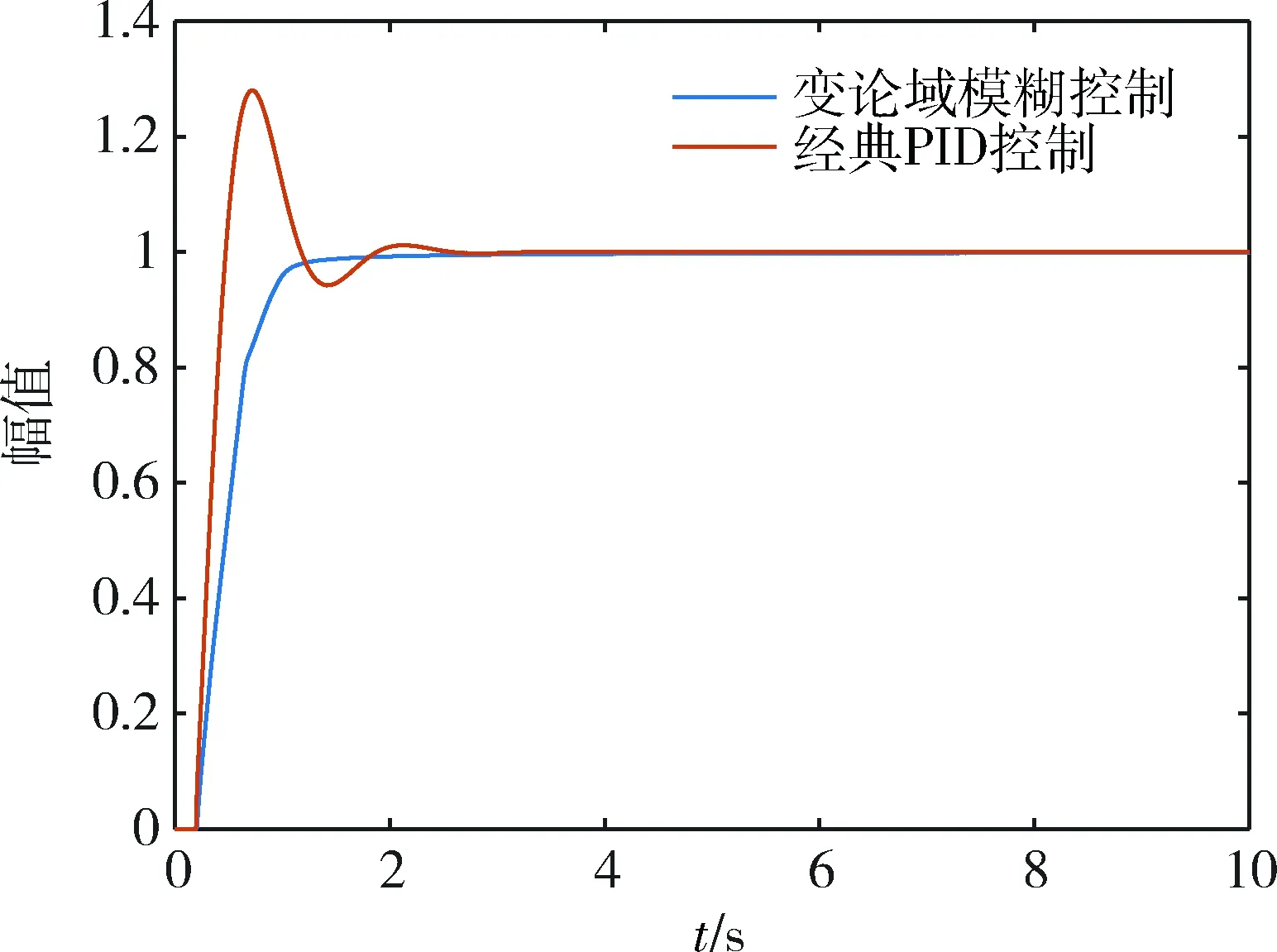
图10 系统阶跃响应仿真结果对比

前馈回路中选择扰动通道传递函数为

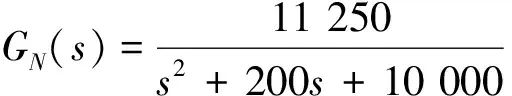
(23)

由式(21)可以得到前馈通路传递函数：

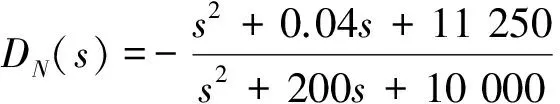
(24)

通过控制系统仿真实验对比经典PID控制器、变论域模糊控制器的单位阶跃响应，阶跃信号在t=0.2 s输入，系统阶跃响应仿真结果对比如图10所示。可以看出：经典PID控制虽然初始阶段上升较快，但超调量较大，且有震荡，最终达到稳态(t=2.7 s)用时较长；而变论域模糊控制很好地改善了稳态性能，同时具备较好的鲁棒性，在t=1 s前后即达到了稳态，无超调，另外在很大程度上兼顾了实际导弹的弹道特性，达到了预期效果。

由于导弹飞行过程中是动态调整的，因此，在t=1 s向系统输入周期为1 s、幅值为0.2的正弦信号，对比分析经典PID控制和变论域模糊控制的正弦跟踪响应仿真结果，如图11所示。可以看出：经过一定时间的调整之后，经典PID控制和变论域模糊控制都能准确地跟踪正弦波形的相位特性，较好地输出正弦波形；但变论域模糊控制输出正弦波形的幅值更准确。

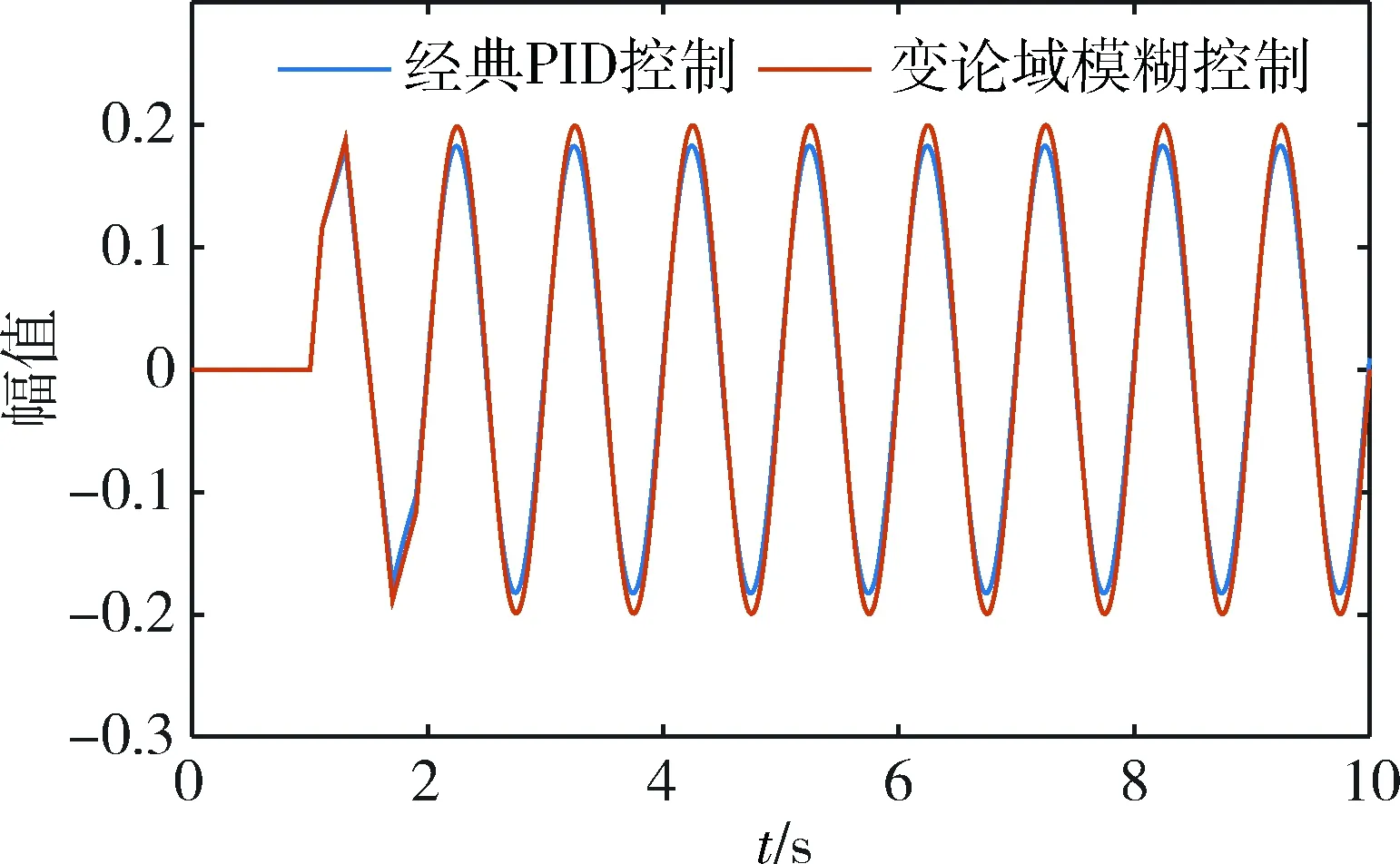
图11 系统正弦跟踪响应仿真结果对比

为验证前馈控制的有效性，在t=5.2 s系统达到稳态时加入扰动信号，对比分析有、无前馈控制时系统对干扰信号的响应特性，如图12所示。可以看出：无前馈控制时，系统输出状态在t=5.2 s有较大变化；而加入前馈控制后，曲线在t=5.2 s前后没有变化，也即前馈回路有效补偿了扰动的影响。

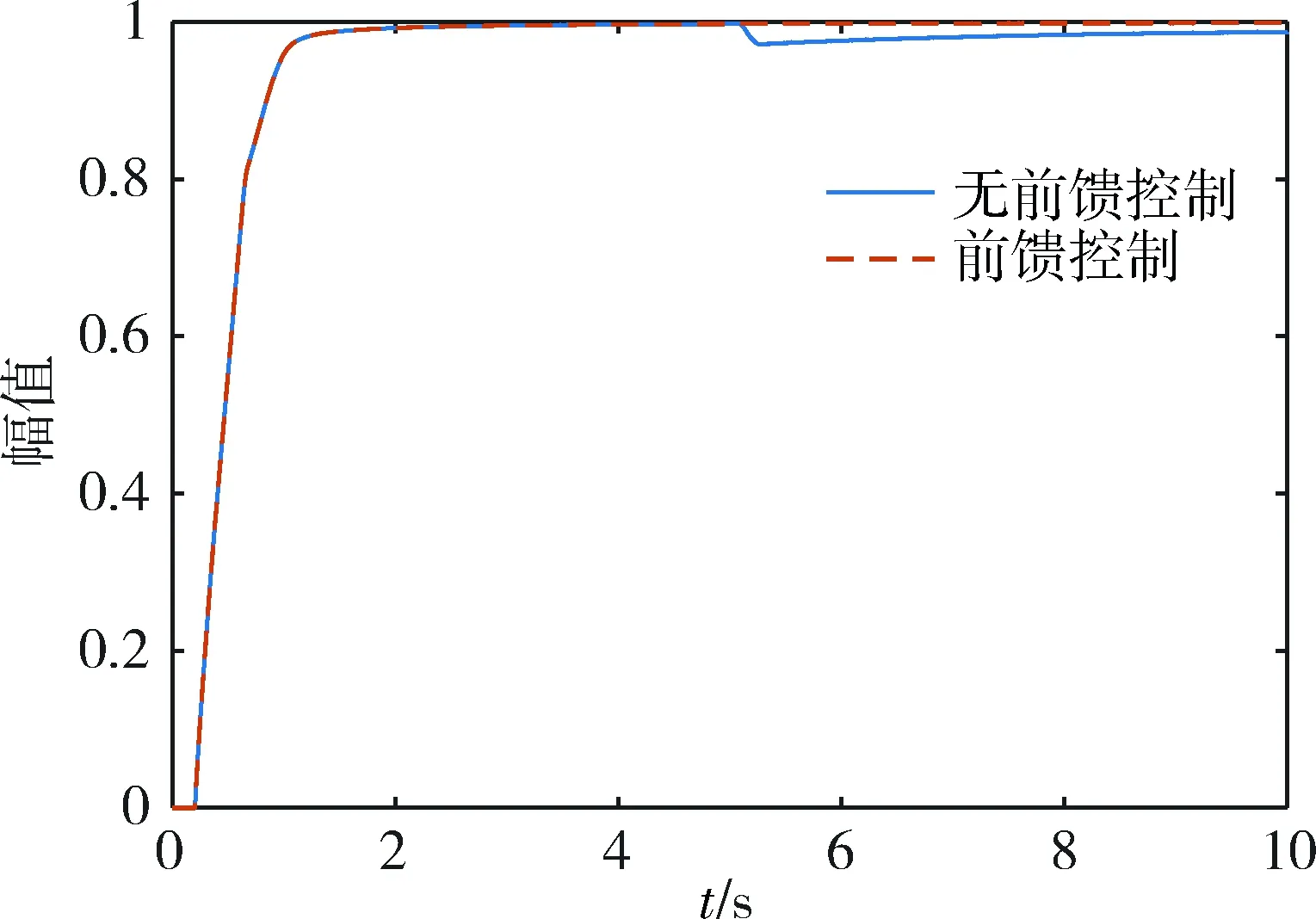
图12 有、无前馈控制时系统对干扰信号的响应特性

[1] 张明月,杨洪波,章家保,等.改进自抗扰控制谐波式电动舵机伺服系统[J].光学精密工程,2014,22(1):99-107.

[2] 付子义,邢阳.无刷直流电机的变论域模糊自适应控制[J]．计算机仿真,2015(5):336-339.

[3] 狄芳,焦仁雷,谈乐斌,等.基于DSP某高炮随动控制系统设计[J]．计算机测量与控制,2014,22(9):2830-2832．

[4] 刘军.数控技术及应用[M].北京:北京大学出版社,2013.

[5] 蒋乐涛.某型数字化随动系统分析及其调测系统设计[D].南京：南京理工大学,2008.

[6] BAO P，XU Z G．The fuzzy controller with on-line self adjustable proportional factor[J]．Process automation instrumentation，2002,8(21):20-22．

[7] ZHANG D.Advances in high performance motion control systems[D].Hong Kong：Hong Kong University of Science and Techno-logy,2009.

[8] 彭树萍,李博,姜润强，等.光电跟踪系统的双模控制[J].光学精密工程,2016,24(2):335-342.

[9] 王国宇,黄植功,戴明,等.基于改进粒子群算法的无刷电机模糊控制研究[J].广西师范大学学报(自然科学版)，2016,34(2):21-27.

(责任编辑: 尚彩娟)

Variable Universe Fuzzy Controller Design of Missile Mark Trajectory with Feed-forward Compensation

DU En-xiang, WANG Shuang-long, CHANG Lei

(Department of Arms Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

In order to accurately control the missile mark trajectory of embedded simulation trainer for a certain type of vehicular missile, the method of converting the control instruction of missile to the control signal of simulation trainer is analyzed, and the mathematical model of control object is built. According to system characteristics, a variable universe fuzzy controller of missile mark trajectory is designed, and the main disturbance and the deficiency of fixture design are compensated by using feed-forward path. In the end, modeling and simulation are done under the environment of MATLAB/Simulink, the unit step response and the sine tracking response are analyzed and compared with classical control method. The results show that the designed controller is more superior in performance and the feed-forward loop is accurate and effective.

variable universe fuzzy control; missile mark trajectory; feed-forward compensation

1672-1497(2017)02-0084-06

2017-03-15

杜恩祥(1966-)，男，副教授，博士。

TP273+4

A

10.3969/j.issn.1672-1497.2017.02.018