钢混结构房屋检测周期理论计算模型研究

■ 王 英 Wang Ying

0 引言

对于房屋安全管理而言，当房屋结构因材料老化、环境侵蚀或使用不当引起累计损伤不能满足安全与正常使用时，需进行结构安全检测鉴定、修缮或加固。调研发现，目前建造年代较早的钢筋混凝土结构房屋安全隐患问题突出，其安全管理现状堪忧。大部分隐患是在房屋使用过程中逐渐出现的，究其原因有如下几点：一是自然老化，建筑材料性能发生耐久性损伤，如混凝土碳化、钢筋锈蚀等，结构性能发生退化；二是缺乏定期的维修和保养；三是设计建造阶段存在缺陷或不足，或施工不当，或使用过程中有不规范装修、改造、违章搭建等。为尽早发现并及时处置房屋存在的安全隐患，有必要定期对房屋进行检测，这对保证结构安全，降低房屋安全事故发生概率具有重要的意义。上海市工程建设规范《房屋修缮工程技术规程》（D G/T J 0 8-2 0 7—2 0 0 8）中给出了房屋结构安全检测周期，但该值主要是在经验总结的基础上提出的，缺少理论依据。因此，对房屋结构安全检测周期进行理论研究，具有重要的理论意义和应用价值。

本文从耐久性理论分析入手，综合考虑建筑材料性能劣化规律、构件使用性、构件安全性（承载力）退化规律以及气候环境特点，建立钢筋混凝土结构房屋安全检测周期理论计算模型。

1 钢筋混凝土结构耐久性研究现状

建筑结构耐久性的研究分为材料层次、构件层次和结构层次。耐久性分析首先从材料入手，获得材料的几何、力学特性随时间变化的规律；再对一定环境下构件的功能函数进行分析，最后由构件的耐久性到实际工程结构的耐久性分析。目前，钢筋混凝土结构耐久性的研究成果多集中在材料和构件层次，包括混凝土碳化、钢筋锈蚀、混凝土冻融破坏、碱-骨料反应、硫酸盐侵蚀、构件抗力时变模型等，获得显著的成果。结构层次的耐久性方面，国内外研究较少。

1.1 混凝土碳化模型

混凝土碳化是一般大气环境下钢筋锈蚀的前提条件。国内外学者通过快速碳化试验、室外暴露试验和实际建筑物调查等方法对碳化系数进行了研究，提出的碳化模型可归为3类：①基于扩散理论建立的理论模型；②基于碳化试验（快速碳化试验、长期暴露试验及实际结构碳化调查）的经验模型 ；③基于扩散理论与试验结果的模型。其中，第三类模型既有充分理论依据，又有实际可操作性，较为合理。目前国内外规范如《混凝土结构耐久性评定标准》（CECS220—2007）、GeneralGuidelinesforDurability DesignandRedesign.ProjectBE95-1347,2000， 提出的碳化模型皆属于第三种模型。

1.2 锈蚀钢筋力学性能

对锈蚀钢筋力学性能的研究主要以试验研究为主，通过对不同锈蚀程度的钢筋进行拉伸试验，统计其力学性能随质量锈蚀率η的变化规律。普遍认为，随着平均锈蚀率的增大，锈蚀钢筋名义屈服/极限强度以及极限应变均发生退化，而相较于强度，锈蚀对极限应变的影响更为显著。一般大气条件下，由混凝土碳化而引起的钢筋锈蚀可认为是均匀的。当截面损失率ηs的范围为5%<ηs<1 2%时，锈蚀钢筋屈服强度fyc与ηs关系见式（1）：

式中，fy—锈蚀前钢筋屈服强度。

1.3 锈蚀构件承载力计算方法

在锈蚀构件承载力计算方法方面，锈蚀钢筋混凝土梁的研究相对较为成熟。目前研究一致认为，钢筋锈蚀造成钢筋混凝土梁承载力降低主要有以下原因：一是混凝土截面损伤；二是钢筋截面损伤及力学性能退化；三是锈蚀引钢筋与混凝土之间的黏结性能退化，导致钢筋与混凝土不能很好地协同工作[1]。不过，对于端部锚固良好的锈蚀钢筋混凝土梁，研究者们发现，黏结性能退化对抗弯承载力基本不产生影响，其极限承载力与锈后最小截面积相关[2-5]。

2 钢筋混凝土结构房屋检测周期理论计算模型研究

2.1 首次检测时间计算模型

从耐久性理论分析入手，综合考虑建筑材料性能劣化规律、构件使用性及安全性退化规律，可建立钢筋混凝土结构房屋首次安全检测时间的理论计算模型。一般大气环境中，引起混凝土结构中钢筋锈蚀的碳化及氯离子渗透是不可避免的，同时钢筋锈蚀引起的结构性能劣化非常显著。因此，混凝土中钢筋锈蚀被认为是当今影响混凝土结构耐久性的首要因素。因此，从使用性要求出发，将钢筋锈蚀的三种耐久性极限状态：钢筋开始锈蚀、混凝土保护层锈胀开裂以及混凝土表面出现可接受最大外观损伤（该状态涵盖了钢筋锈蚀以及冻融等损伤）作为确定结构首次安全检测时间需考虑的时间点。另外，从安全性要求出发，将钢筋锈蚀或混凝土冻融损伤至一定程度作为需考虑的时间点。《混凝土结构耐久性评定标准》（CECS220—2007）指出，当锈蚀构件受力钢筋截面损失率ηs超过6%时，应对构件进行承载力验算。由此建立的房屋结构首次安全检测时间计算模型见图1。由图可知：①若房屋构件在使用年限内不允许钢筋锈蚀或严格不允许保护层锈胀开裂（记为第一类），则首次检测时间为钢筋开始锈蚀时间ti；②若房屋构件在使用年限内一般不允许出现锈胀裂缝（记为第二类），则首次检测时间为混凝土保护层锈胀开裂的时间t c r和构件钢筋达到需要进行承载力验算的截面损失率（6%）时对应时间t0间的较小者；③若房屋构件在使用年限内允许出现锈胀裂缝或局部破损（记为第三类），则首次检测时间为混凝土表面出现可接受最大外观损伤的时间td和t0间的较小者。

计算t0时要考虑混凝土开裂前后钢筋锈蚀速率不同。

2.2 第二次、第三次检测时间计算模型

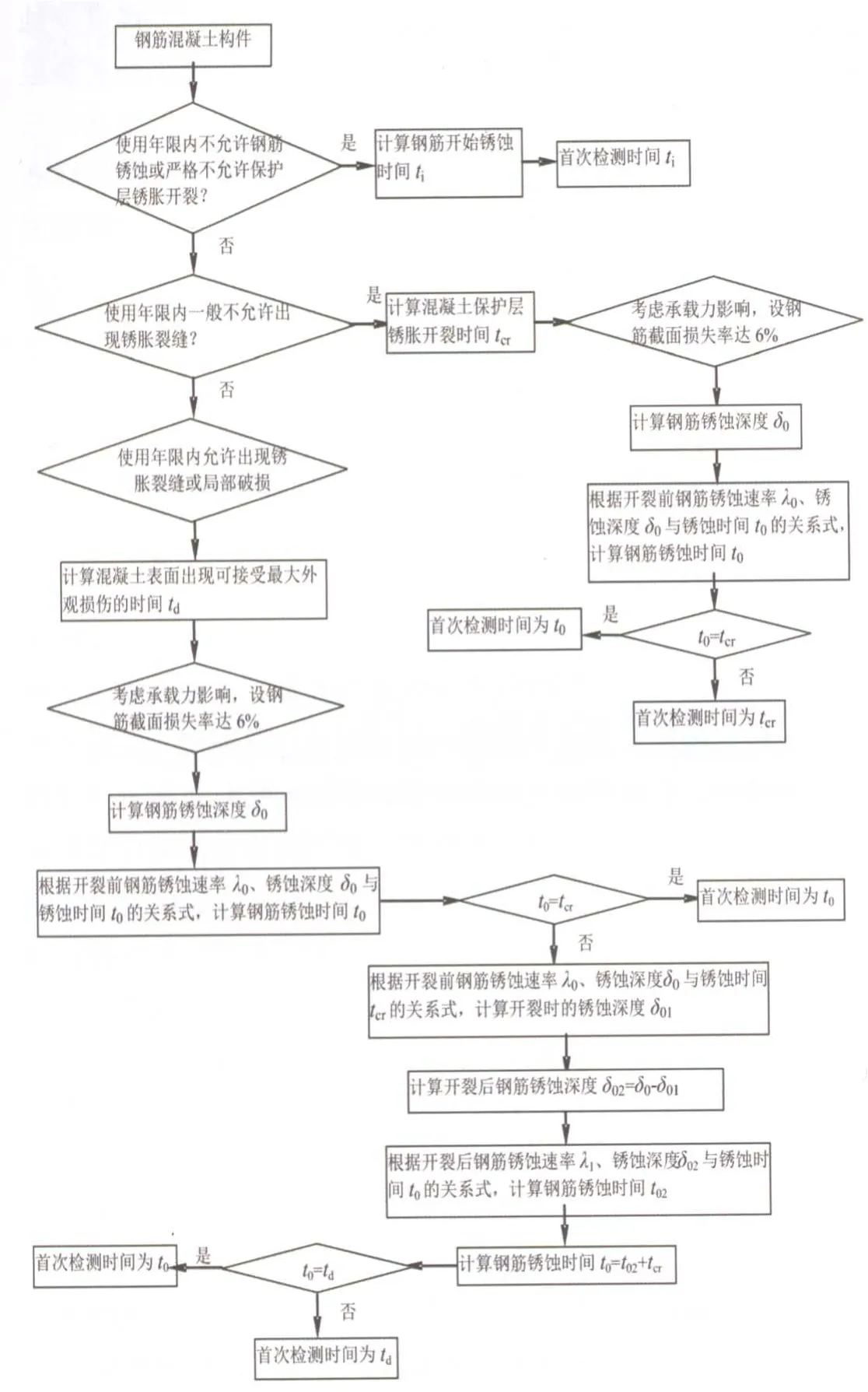
图1 钢筋混凝土结构构件首次安全检测时间理论计算模型

理论上，房屋经过首次安全检测后，结构若能恢复至刚建造时的状态，则第二次与首次安全检测时间的间隔应与首次检测时间相同。然而，房屋是不可能恢复至初始状态的。实际上，在经过了首次检测后，通常会对达到耐久性极限的构件进行修缮，虽不可能恢复到初始状态，但这些构件已不至于保持原来的劣化速度继续劣化。然而，未经过修缮的构件却是保持原有速度劣化的。考虑到这一点，不妨认为房屋结构构件的耐久性和承载力都保持原有速度发生劣化。这样确定的第二次、第三次检测时间是偏于安全的。

房屋结构的第二次、第三次检测时间可综合考虑结构构件达到的不同耐久性极限状态及承载力损失程度来确定。计算分析可知，结构的首次安全检测实际是由构件的使用性决定的。当构件锈蚀损伤严重，影响构件承载力甚至危及结构安全时，也需进行结构安全检测。这里认为构件承载力变为原来的9 5%（对应时间t0）以及9 0%（对应时间t0'）需进行检测，t0与t0'计算方法相同。由此，确定3类房屋的检测周期，见图2。

3 钢筋混凝土结构房屋检测周期理论计算

3.1 钢筋开始锈蚀的时间

试验和工程检测表明，碳化深度尚未到达钢筋表面时，钢筋可能已经锈蚀。结构建成至钢筋开始锈蚀的时间ti可按（2）式估算：

式中，kk、kc、km分别为碳化速率、保护层厚度、局部环境对钢筋开始锈蚀时间的影响系数，可查表确定。其中，碳化速率影响系数kk与碳化系数k经拟合关系式见式（3）：而碳化系数k可按（4）式计算：

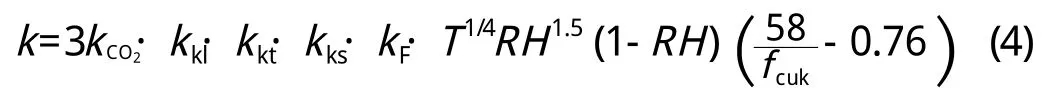
式中， k—碳化系数（(mm/√a)）；

kCO2—C O2浓度影响系数；

kkl—位置影响系数，构件角区取1.4，非角区取1.0；

kkt—养护浇筑影响系数，取1.2；

kks—工作应力影响系数，受压时取1.0，受拉时取1.1；

kF—粉煤灰取代系数，对掺有I级粉煤灰、低水胶比的高密实混凝土，可取1.0；

T—环境温度（℃）；

R H —环境相对湿度；

fcuk—混凝土强度标准值。

3.2 混凝土保护层锈胀开裂的时间

混凝土保护层锈胀开裂时间tcr可按（5）式估算：

式中， δcr—保护层锈胀开裂时的临界钢筋锈蚀深度（mm）；

λ0—保护层锈胀开裂前的年平均钢筋锈蚀速率（mm/a）。

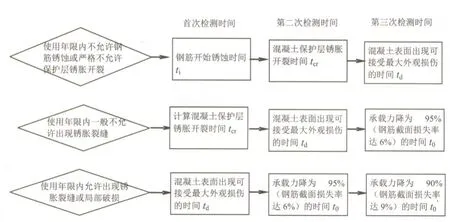
图2 钢筋混凝土结构构件安全检测周期理论计算模型

将式（5）进行简化，tcr可简化计算见式（6）：

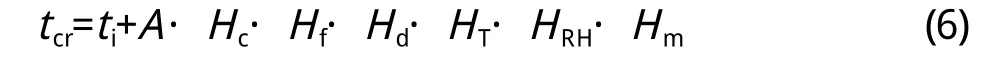
式中， A—特定条件下（各项影响系数为1.0时）构件自钢筋开始锈蚀至保护层锈胀开裂的时间（a），对室外杆件取1.9，室外墙、板取4.9；对室内杆件取3.8，室内墙、板取1 1.0；

Hc、Hf、Hd、HT、HRH、Hm—分别为保护层厚度、混凝土强度、钢筋直径、环境温度、环境湿度、局部环境对保护层锈胀开裂时间的影响系数，可查表确定。

经拟合，HT与T 、HRH与R H 关系见式（7）。

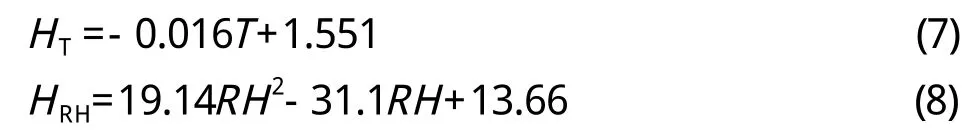
3.3 混凝土表面出现可接受最大外观损伤的时间

混凝土表面出现可接受最大外观损伤（裂缝宽度达2～3 mm）的时间td可按（9）式估算：

式中，δd—混凝土表面出现可接受最大外观损伤时的钢筋锈蚀深度（mm），

将式(9)进行简化，则td可简化计算见式（1 0）：

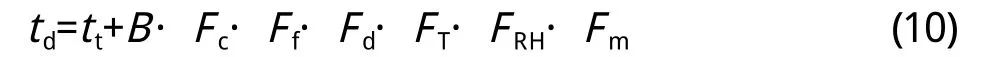
式中， td—混凝土表面出现可接受最大外观损伤的时间（a）；

B—特定条件下（各项影响系数为1.0时），自钢筋开始锈蚀至混凝土表面出现可接受最大外观损伤的时间（a），对室外杆件，B取7.0 4，室外墙、板，B取8.0 9，对室内杆件，B取8.8 4，室内墙板，B取1 4.4 8；

Fc、Ff、Fd、FT、FRH、Fm—分别为保护层厚度、混凝土强度、钢筋直径、环境温度、环境湿度、局部环境对混凝土表面出现可接受最大外观损伤时间的影响系数，可查表确定。

其中，经拟合，FT与T、FRH与R H所示关系见式（1 1）（1 2）：

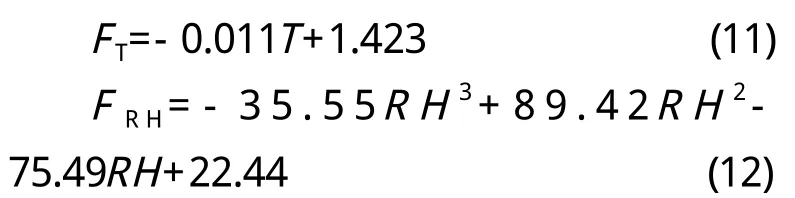
3.4 钢筋截面损失对应的时间

当构件锈蚀损伤严重，受力钢筋截面损失率ηs超过6%，应对构件进行承载力验算。ηs为6%时，根据式(1)，锈蚀钢筋屈服强度fcy大约与未锈钢筋屈服强度fy相等。对于全跨不均匀锈蚀或仅部分区段锈蚀的钢筋混凝土梁，绝大多数情况下钢筋端部的锚固能够得到保证，则黏结性能退化对梁抗弯承载力基本不产生影响[2]。因此，根据锈蚀钢筋混凝土梁抗弯承载力计算公式，钢筋混凝土梁锈蚀后的抗弯承载力约为锈蚀前的9 5%。对于轴拉构件，经计算，锈蚀后极限抗拉承载力约为锈蚀前的9 4%。

根据截面损失率ηs的定义，ηs与钢筋锈蚀深度δ0的关系可由式(1 3)所示：

式中，d为未锈蚀钢筋直径。根据式(1 3)，ηs为6%时，δ0为原未锈蚀钢筋直径d的1.5%。

计算构件钢筋截面损失率为6%对应的时间t0时要考虑混凝土开裂前后钢筋锈蚀速率的不同。已知钢筋年平均钢筋锈蚀速率、锈蚀深度δ0与锈蚀时间t0间有如下关系式：

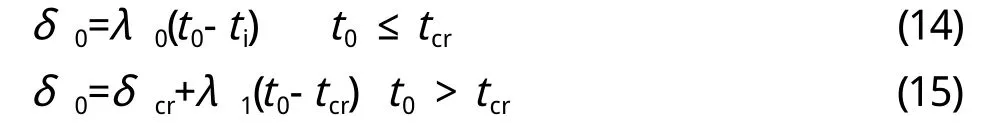
式中，tcr—混凝土保护层开始锈胀开裂的时间；

λ0—保护层锈胀开裂前年平均钢筋锈蚀速率；

λ1—保护层锈胀开裂后年平均钢筋锈蚀速率；

δcr—临界钢筋锈蚀深度。

对于室外杆件：

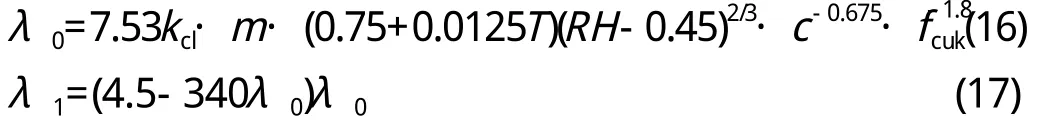
式中，kcl—钢筋位置影响系数，钢筋位于角部时取1.6，钢筋位于非角部时取1.0；λ1<1.8λ0时，取λ1=1.8λ0。

若ηs达6%时的时间先于混凝土保护层开始锈胀开裂的时间，应采用λ0计算。根据式(1 4)，可得：

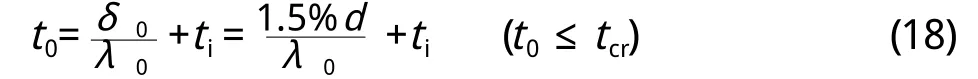
若截面损失率ηs达6%时的时间t0晚于混凝土保护层锈胀开裂的时间tcr。则计算t0时应采用λ1计算。此时，先计算混凝土保护层开裂前钢筋锈蚀深度δ01。根据式(5)和式(1 4)，

则，混凝土保护层开裂后的钢筋锈蚀深度δ02为：

式中，δcr—临界钢筋锈蚀深度。

由式(1 5)可知，混凝土保护层开裂后钢筋锈蚀时间t02为：

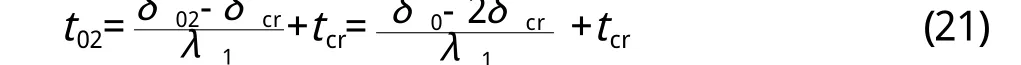
则截面损失率ηs达6%时的时间t0为：

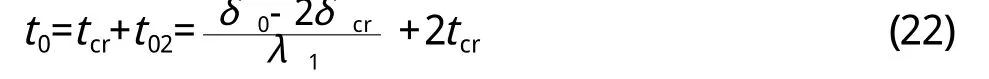
4 上海钢筋混凝土结构房屋首次安全检测时间

以上海为例，计算其钢筋混凝土结构房屋的安全检测周期。上海市年平均气温和相对湿度地区差异较小,其中，2 0 1 5年年平均气温T为1 7.0℃，年平均相对湿度R H为7 4%。

4.1 钢筋开始锈蚀时间ti

以 室 外 杆 件 为 例，kCO2=1.4；kkl=1.4；kkt=1.2；kks=1.0 ；kF=1.0；fcuk考虑范围1 0~4 0 MP a。则，根据式(4)，碳化系数k为：

根据式(3)，计算可得混凝土强度对应的碳化速率影响系数kk和碳化系数k（表1）。

m取4.5，km=0.6 8，保护层厚度考虑5~4 0 mm；则，根据式(2)，计算得室外杆件钢筋开始锈蚀时间ti，见表2。由表2可知，混凝土强度越小，保护层厚度越小，钢筋开始锈蚀时间越早。室外杆件钢筋开始锈蚀时间为1 6.5年（平均值）。同理，可计算室内杆件、室外墙板、室内墙板的钢筋开始锈蚀时间，分别为1 6.7年、2 0.1年，2 0.3年。

4.2 混凝土保护层锈胀开裂的时间tc r

对于室外杆件，A=1.9；HT=1.2 8 ，HRH=1.1 3 。m取4.5，Hm=0.8 3。考虑混凝土强度1 0～4 0 MP a，钢筋直径4～2 8 mm，混凝土保护层厚度5～4 0 mm。则，根据式(5)计算混凝土保护层锈胀开裂的时间 ，结果为2 4.7年（平均值）。

表1 混凝土强度对应的碳化系数k和碳化速率影响系数kk

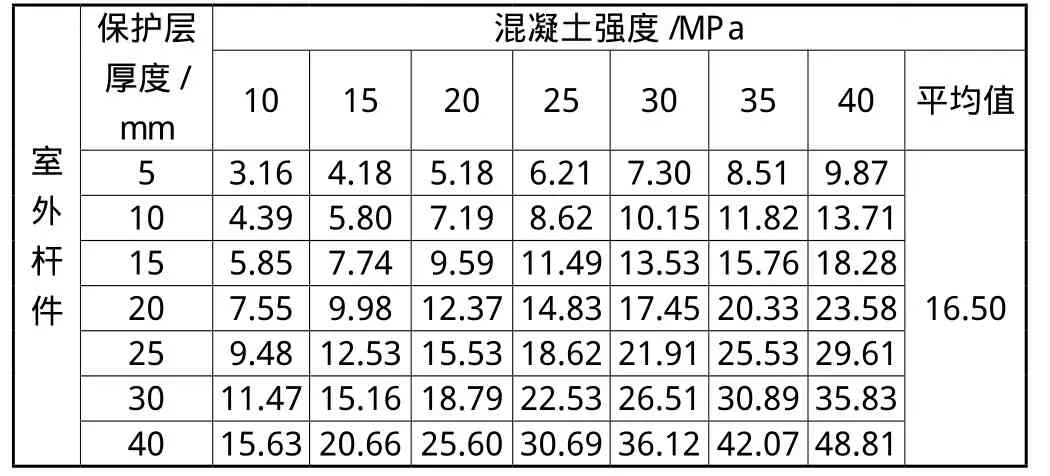
表2 钢筋开始锈蚀时间ti

同理，可计算室内杆件、室外墙板、室内墙板的混凝土保护层锈胀开裂时间，分别为：3 9.7年、4 5.2年、8 6.2年。

4.3 混凝土表面出现可接受最大外观损伤的时间td

对于室外杆件， B=7.04，FT=1.2 4 ，FRH=1.1 0 。m取4.5，查表可知Fm=0.8。考虑混凝土强度10～40MPa，钢筋直径4～2 8 mm，混凝土保护层厚度5～40mm。则，根据式(1 0)，计算混凝土表面出现可接受最大外观损伤的时间td，结果为3 1.6年（平均值）。

同理，可计算室外墙板、室内杆件、室内墙板混凝土表面出现可接受最大外观损伤的时间，分别为4 4.6年、5 6.2年、9 2.5年。

4.4 钢筋截面损失对应的时间

假定ηs达6%时的时间先于混凝土保护层开始锈胀开裂的时间，则采用λ0计算。对于室外杆件，kcl=1.6，m=4.5，则：

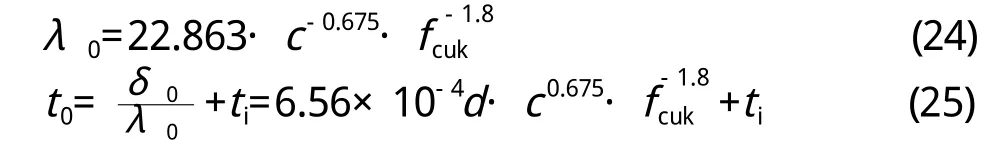
同理，可推导室外墙板、室内杆件、室内墙板截面损失率ηs达6%的时间t0。由对应位置上的值比较可知，t0要晚于tcr。因此，计算t0时应采用混凝土开裂后的钢筋锈蚀速率λ1。

对于室外杆件：

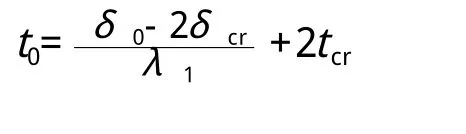
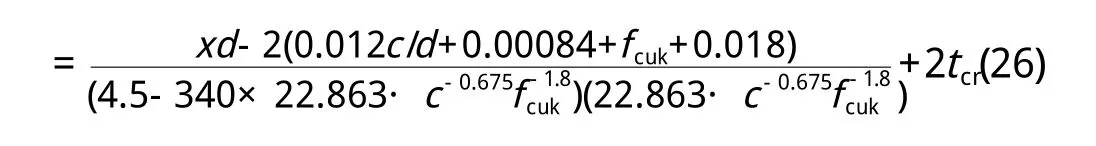
同理，可推导室内杆件、室外墙板、室内墙板截面损失率ηs达6%时的时间t0的计算公式。经过计算，室外杆件、室内杆件、室外墙板、室内墙板的t0分别为：5 5.5年、9 3.9年、9 8.8年、1 2 8.7年。

当构件承载力变为原来的9 0%时，对应钢筋截面损失率ηs分别约为9%。由式(1 3)可知，钢筋锈蚀深度δ0达原直径的2.3%。经推导，可计算室外杆件、室内杆件、室外墙板、室内墙板截面损失率ηs达9%时的钢筋锈蚀时间t0'，分别为：6 2.3年、1 0 8.1年、1 0 9.5年、1 6 9.4年。

4.5 上海市钢筋混凝土结构房屋安全检测周期

根据计算结果，3类房屋的结构安全检测周期见表3。处于安全考虑，各次检测时间取室外杆件、室内杆件、室外墙板、室内墙板等4类构件中的最小值。

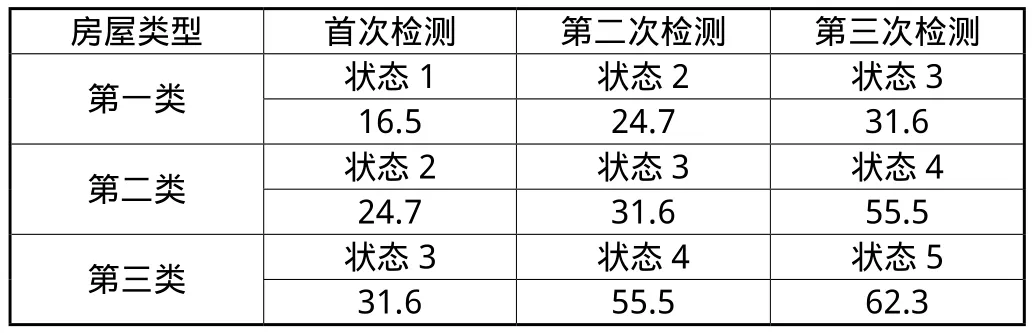
表3 上海市钢筋混凝土结构房屋检测周期（年）（理论计算值）

对于居住类房屋，通常为使用年限内允许出现锈胀裂缝或局部破损的房屋，即第三类房屋。从计算结果看，该类房屋首次检测时间约为3 0年，第二次检测时间约为5 0年。这与结构5 0年的设计基准期是较为符合的，即在设计基准期内，不经过大的维修和加固，结构不会出现危险构件，可以继续使用。这与实际情况也较为相符，因此计算结果是较为合理的，从而验证了本文提出的检测周期理论计算模型的合理性。

5 结语

（1）本文在钢筋混凝土结构耐久性研究现状分析的基础上，综合考虑构件的使用性、安全性，考虑实际气候环境条件，建立钢筋混凝土结构房屋结构安全检测周期理论计算模型，将钢筋开始锈蚀时间、混凝土保护层锈胀开裂的时间、混凝土表面出现可接受最大外观损伤的时间、构件承载力因受力钢筋锈蚀降低至原来的9 5%、9 0%（对应受力钢筋截面损失率ηs约6%、9%）的时间作为结构检测时间点。

（2）以上海为例，采用推导的公式，考虑构件位置、构件工作环境、温度、湿度、碳化速率、钢筋锈蚀速率、混凝土强度、混凝土保护层厚度、钢筋直径等影响参数，计算获得上海钢筋混凝土结构房屋安全检测周期。计算结果与结构5 0年的设计基准期是较为符合的，从而验证了本文提出的检测周期理论计算模型的合理性。

（3）本文理论计算模型考虑的房屋是新建钢筋混凝土结构房屋，房屋不存在材料、设计、施工等质量问题，且仅考虑一般大气环境影响造成材料性能劣化的情况。对于建造时间较早的房屋，其设计建造标准偏低，房屋施工质量较差，房屋在长期使用过程中可能存在违规装修和改造、改变使用用途、缺少精心的维修和保养等，此时房屋安全会受到相应不利影响。上述情况在确定房屋检测周期建议值时要予以考虑。

参考文献：

[1]Rodriguez J, Ortega L, Garcia A, Corrosion of reinforcingbars and service life of R/C structures: Corrosion and bonddeterioration[C]. Proceding of International Conference onConcrete across Borders, Vol. II, 1994, pp.315-326.

[2]Gu X.L., Zhang W.P., Shang D.F., et al. Flexural behaviorof corroded reinforced concrete beams[A]. Proc., 12th Int.Conf. on Engineering, Science, Construction, and Operations inChallenging Environments-Earth and Space 2010. G. B.Song,and R.B. Malla, eds.,Honolulu, U.S.A., 3545-3552.

[3]王晓刚,顾祥林,张伟平.锈蚀钢筋混凝土梁抗弯性能数值模拟[J].建筑科学,工程学报, 2009, 26(1): 49-54.

[4]Malumbela G., Alexander M. and Moyo P., Variation of steelloss and its effect on the ultimate flexural capacity of RC beamscorroded and repaired under load [J]. Construction and BuildingMaterials, 2010, 24(6): 1051-1059.

[5]Rio O., Andrade C., Izquierdo D., et al. Behaviour of patchrepaired concrete structural elements under increasing static loadsto flexural failure [J]. Journal of Materials in Civil Engineering,2005, 17(2): 168-177.