有限长加筋圆柱壳水下声辐射的精细传递矩阵法

王献忠，江晨半，计方，方月明

（1.高性能船舶技术教育部重点实验室（武汉理工大学），武汉430063；2武汉理工大学交通学院，船舶、海洋与结构工程系，武汉430063；3.中国舰船研究院，北京100192）

有限长加筋圆柱壳水下声辐射的精细传递矩阵法

王献忠1，2，江晨半2，计方3，方月明2

（1.高性能船舶技术教育部重点实验室（武汉理工大学），武汉430063；2武汉理工大学交通学院，船舶、海洋与结构工程系，武汉430063；3.中国舰船研究院，北京100192）

基于传递矩阵法，结合非齐次项的精细积分方法，提出了一种求解加筋圆柱壳动响应的精细传递矩阵方法。该方法基于圆柱壳结构的一阶振动微分方程，得到加筋圆柱壳的场传递矩阵和点传递矩阵，结合非其次项的精细积分方法和增维存储的办法考虑广义声压激励的作用。利用流固耦合交界面处的连续条件，实现声压系数的求解。开展了模态收敛性分析，并将数值计算结果与试验结果进行对比，验证方法的有效性。同时分析了边界条件及环肋数目等对声辐射的影响。

加强筋；圆柱壳；声辐射；精细传递矩阵法

0 引言

有限长加筋圆柱壳是潜艇，鱼雷等水下航行体的典型结构形式，其结构噪声主要来源于机械设备振动激励壳板进而辐射噪声到水中。因此，研究机械激励下水中有限长环肋圆柱壳的声振特性，是国内外研究的热点。关于水中圆柱壳的振动和声辐射特性计算方法有关研究人员已经进行了大量的理论研究。Stepanishen[1]研究了有限长圆柱壳的声辐射计算模型，将壳体位移函数用模态展开，采用模态叠加法和Green函数得到耦合振动方程，计算分析了圆柱壳的声辐射自阻抗和互阻抗。Sandman[2-3]认为柱型障板对有限长圆柱壳表面声压沿轴向分布有一定的影响，而对模态辐射阻抗的影响可以忽略，带圆柱形障板的圆柱壳可作为一种合理的近似预报模型。Laulagnet[4-5]采用能量法处理肋骨，研究了流场中有限长环肋圆柱壳的声辐射特性，并讨论了肋骨参数对声辐射的影响。但上述解析方法均是只能求解等厚度圆柱壳计算模型，对于任意边界条件,轴向变厚度圆柱壳，变截面壳体等结构的振动与声辐射问题，由于结构振动控制方程的复杂性使得解析方法在这些方面仍然存在一定的困难。

Irie等人解决了变厚度锥壳[6]、锥柱结合壳[7]、轴向具有离散弹簧支承的圆柱壳[8]等各类结构的谐振问题。但这些研究均是围绕结构的固有振动特性进行展开研究的，并没有考虑水下声辐射的问题。

本文基于传递矩阵法[6]和精细积分法[9-10]联立给出一种精细积分传递矩阵法，并将其应用到求解水下有限长加筋圆柱壳的振动与声辐射问题，该方法可推广到锥壳结构，锥-柱组合壳等细长体结构的振动声辐射，其计算固有频率与文献及有限元值进行对比，将计算的辐射声压与文献值进行对比，验证方法的有效性。在此基础上，开展了环肋和边界条件对水下环肋圆柱壳的声辐射的影响研究。

1 加筋圆柱壳的传递矩阵

根据Flügge壳体理论[6]，可得到力的平衡方程：

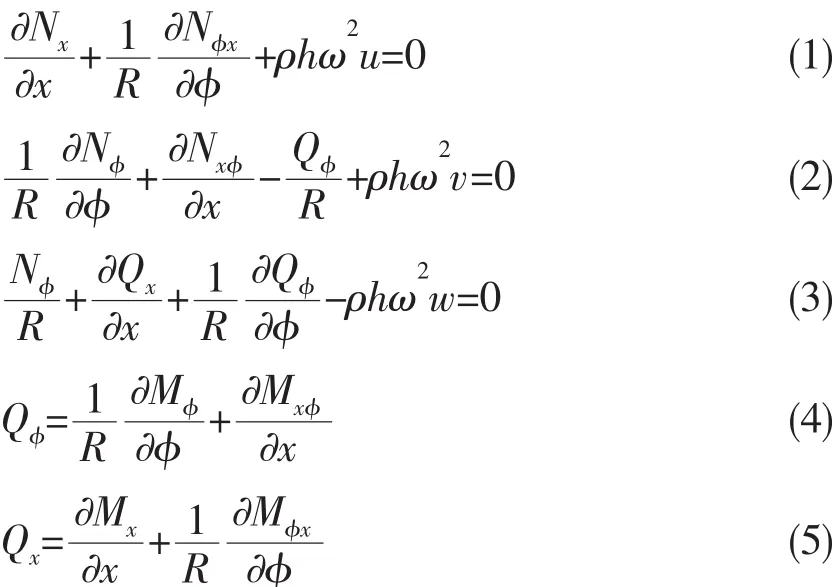
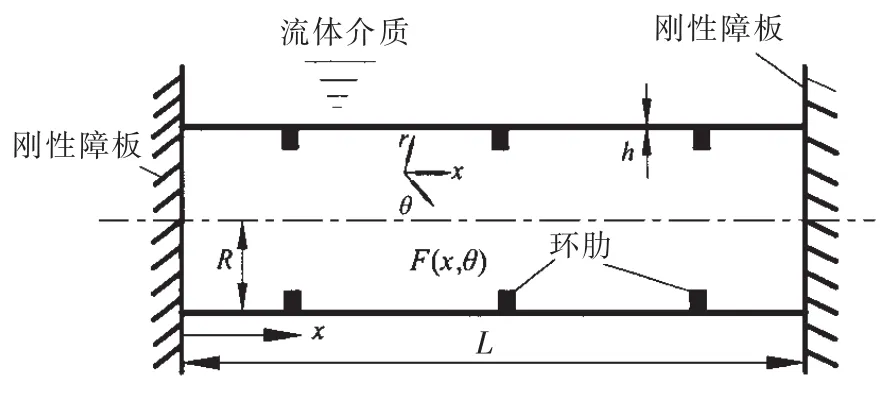
图1 环肋柱壳模型和坐标示意图Fig.1 An stiffened cylindrical shell geometry and coordinate system

其中：Kevin-Kirchhoff膜力，剪力及所有内力可参见文献[5]。

通过将位移和内力进行无量纲化，未知量沿周向展成三角函数的形式：

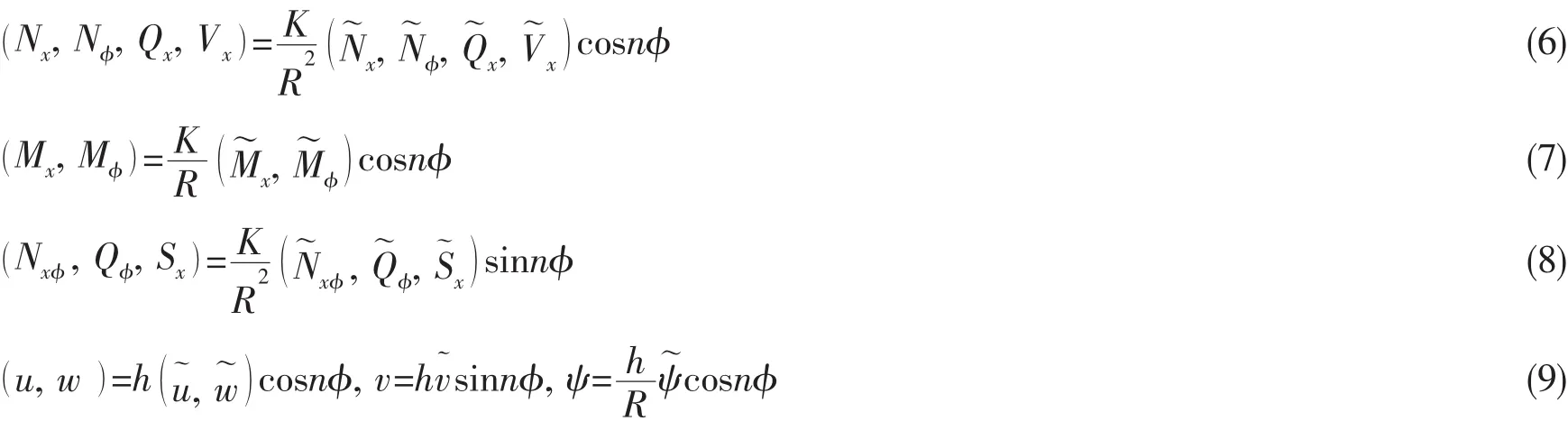
其中：n为周向波数，并引入以下无量纲长度参数和频率因子。

通过消去8个未知量Nφ，Nφx，Nxφ，Mxφ，Mφx，Mφ，Qx，Qφ，保留8个未知分量：轴向位移u，切向位移v，径向位移w，转角φ，轴向力Nx，弯矩Mx，剪力Vx，切向力Sx这些状态向量。经过复杂的化简和对8个未知量消去后，可得一阶矩阵微分方程形式

环肋对圆柱壳的作用主要体现在状态向量的变化上，当圆柱壳振动时，与壳体连接在一起的环肋会作四种形式的振动，其中两种是面内运动即面内的弯曲和拉伸振动，另外两种是面外运动即面外的弯曲和扭转振动[14]。令Fu、Fv、Fw和Mφ分别表示圆柱壳对环肋的纵向、切向和径向的反作用力及力矩。分别表示环肋对圆柱壳的纵向、切向和径向的反作用力及力矩。根据壳体面板与环肋连接处的位移连续性条件，可将方程组中的状态向量无量纲化可得：

其中：R为肋骨形心半径，R=R+e，e为偏心距。由（12）-（15）式可得在某一环肋位置ξ处，环肋左端

bbk右端由于环肋的存在导致两个面内力和两个面外力发生变化，满足如下式子：

2 精细传递矩阵方法

外流场中声压满足Helmholtz方程及Sommerfeld边界条件：

对于声压场，用分离变量法求解Helmholtz方程，并考虑辐射条件及壳壁处的耦合边界条件，则圆柱壳外部声场中的声压展开式有如下形式的解

利用精细区段的加法定理能够求出非齐次项的精细结果。从推导可知，由于没有假定结构的位移模式，而是直接从壳体振动微分方程出发，因此推导的传递矩阵是精细传递矩阵，误差只来自于E（）l的求解不可能取无穷多项，实际计算时，一般取4项就满足要求。本文以文献[14]圆柱壳为例，计算式（30）取不同项数时某一分段的场传递矩阵行列式结果值。由于行列式结果在1附近，故文中给出了行列式随所取项数的变化，如图2所示。

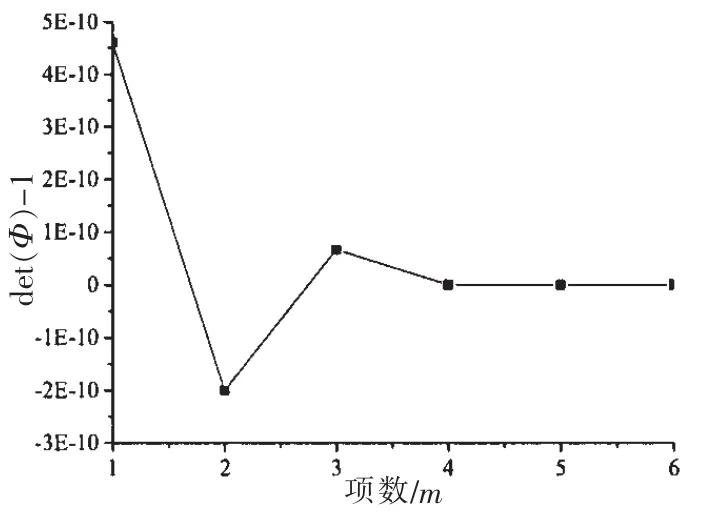
图2 行列式结果随取的项数的变化曲线Fig.2 Matrix determinant curve with the number of items m

圆柱壳受到的机械激励力设为集中力，力作用点为（x0, θ0），故外界激励力表达式为：

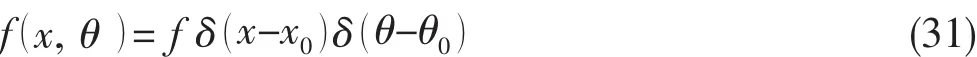
将上式进行正交变换可得：

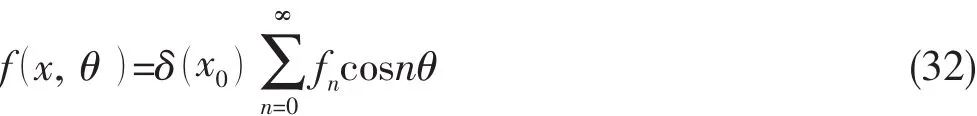
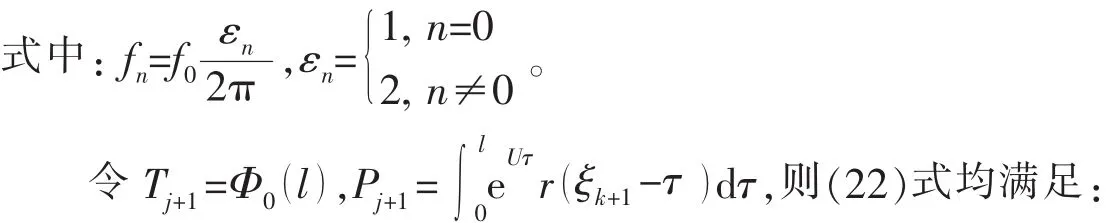
进而可得：

对于该（34）式来说，可根据外激励力及两端边界条件进行求解。为便于编程，可将柱壳离散时考虑在状态向量突变处，例如环肋、激励力作用的位置处进行离散。

根据线性叠加原理，对应于任意阶周向波数n下的径向位移[14]满足：

由于结构界面处上任意一点均满足连续条件，可沿结构长度方向取M个插值点，其中M既要大于波数m，又要满足m=2πλ-1。首先取M个点代入到方程（36）中，再将（20）、（35）式代入（36）式中，则可转化为求解各波数对应的声压系数的方程：

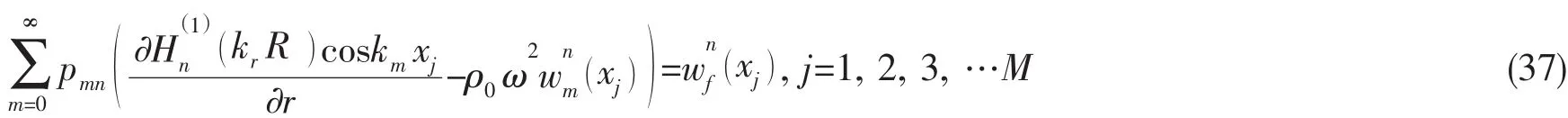
通过最小二乘法或者广义求逆法求解pmn，然后代入到方程（20）中，即可得到流场中的辐射声压。

同时，由（q,n）阶振动模态引起的产生的（m,n）阶声压[16]：

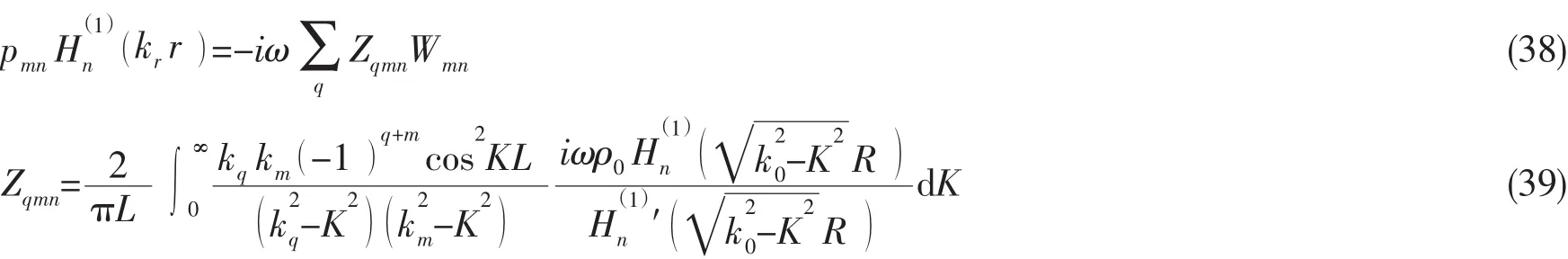
其中：Wmn为对应径向位移的系数，满足是（q,n）阶和（m,n）阶模态的互辐射阻抗。自辐射阻抗（q=m）远大于互阻抗（q≠m），可简化互辐射阻抗表达式：

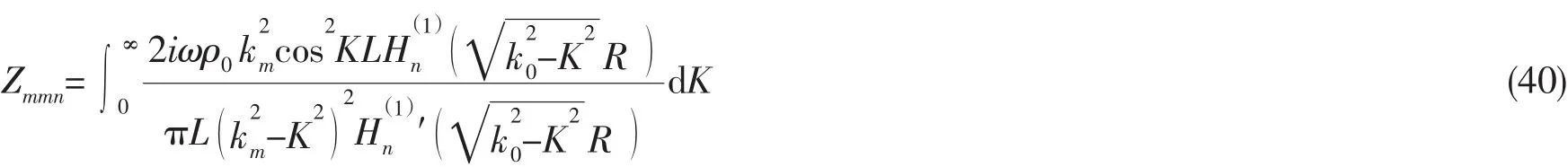
辐射声功率定义为：

结构表面的平均振速定义为：

辐射效率定义为：

声功率级、径向均方速度级和辐射效率级分别定义为：

式中：声功率级的基准Po为0.67×10-18（W），速度级为5×10-8（m/s）。根据（44）式求解得到加筋圆柱壳的水下辐射声功率级、平均振速级及辐射效率级。

3 数值计算

计算结果的收敛性涉及模态截取问题，本文选取的计算模型为环肋圆柱壳结构，结构参数为：圆柱壳长L=0.6 m，半径R=0.2 m，厚度H=3 mm，柱壳的内肋为2 mm×30 mm，肋间距为0.2 m，初始加强筋的位置0.2 m，径向激励力作用在内壳（L/2,0）处，幅值为1 N。测量点为（L/2,0,1.2 m）。计算模型壳体、环肋材料相同，其弹性模量E=2.06e11N/m2，泊松比μ=0.3，密度ρ=7 850 kg/m3，损耗因子η=0.01。流体的密度ρ0=1 000 kg/m3，声速度c0=1 500 m/s。边界条件为两端简支，计算频率为40～40 kHz。

为了验证本文方法的有效性，本文取文献[15]中给的圆柱壳计算模型进行对比计算。该圆柱壳的结构参数为：壳长L=0.6 m，半径R=0.175 m，厚度H=2 mm，径向激励力作用在内壳（L/2,0）处，幅值为1 N。水听器安装在距壳体外面1 m处，测量频率f=4 kHz。计算模型壳体，环肋材料相同，其弹性模量E=2e11N/m2，泊松比μ=0.3，密度ρ=7 850 kg/m3，损耗因子η=0.01。流体的密度ρ0=1 000 kg/m3，声速度c0=1 500 m/s。边界条件为两端简支。本文采用精细传递矩阵法求解该圆柱壳模型的水下声辐射声压，并将计算结果与文献[15]中给出的测试结果和解析结果进行对比，计算结果见图4。

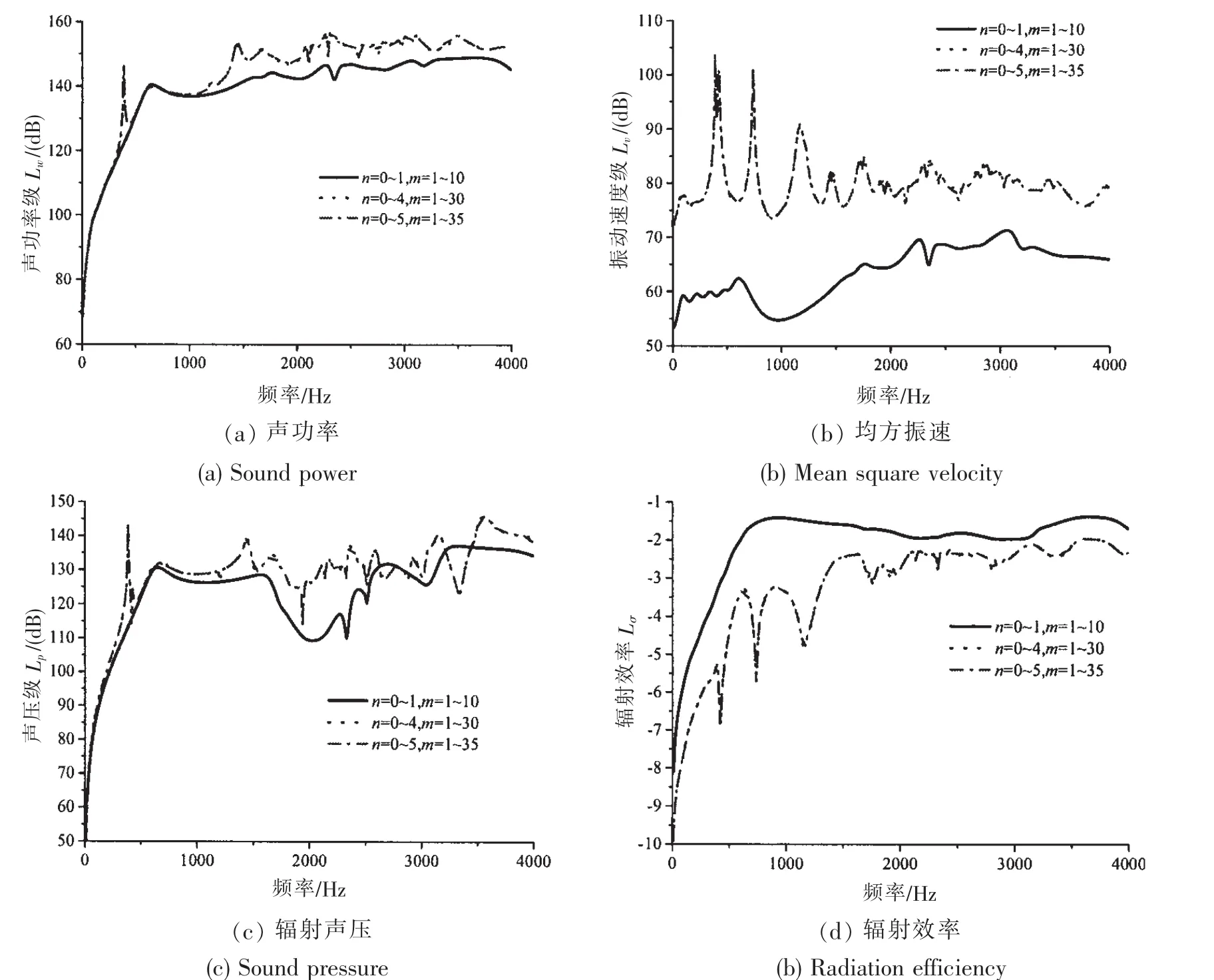
图3 模态截断对加筋圆柱壳振动声辐射的影响Fig.3 Influence of cutting off modality on the vibro-acoustic responses

从图4中对比结果可知：本文方法与试验测量值除了局部角度存在一定差异，但与文献[5]中解析方法得到的计算结果相比较，整体上吻合良好。这说明本文提出的精细传递矩阵法在求解环肋柱壳时具有很好的精确度。

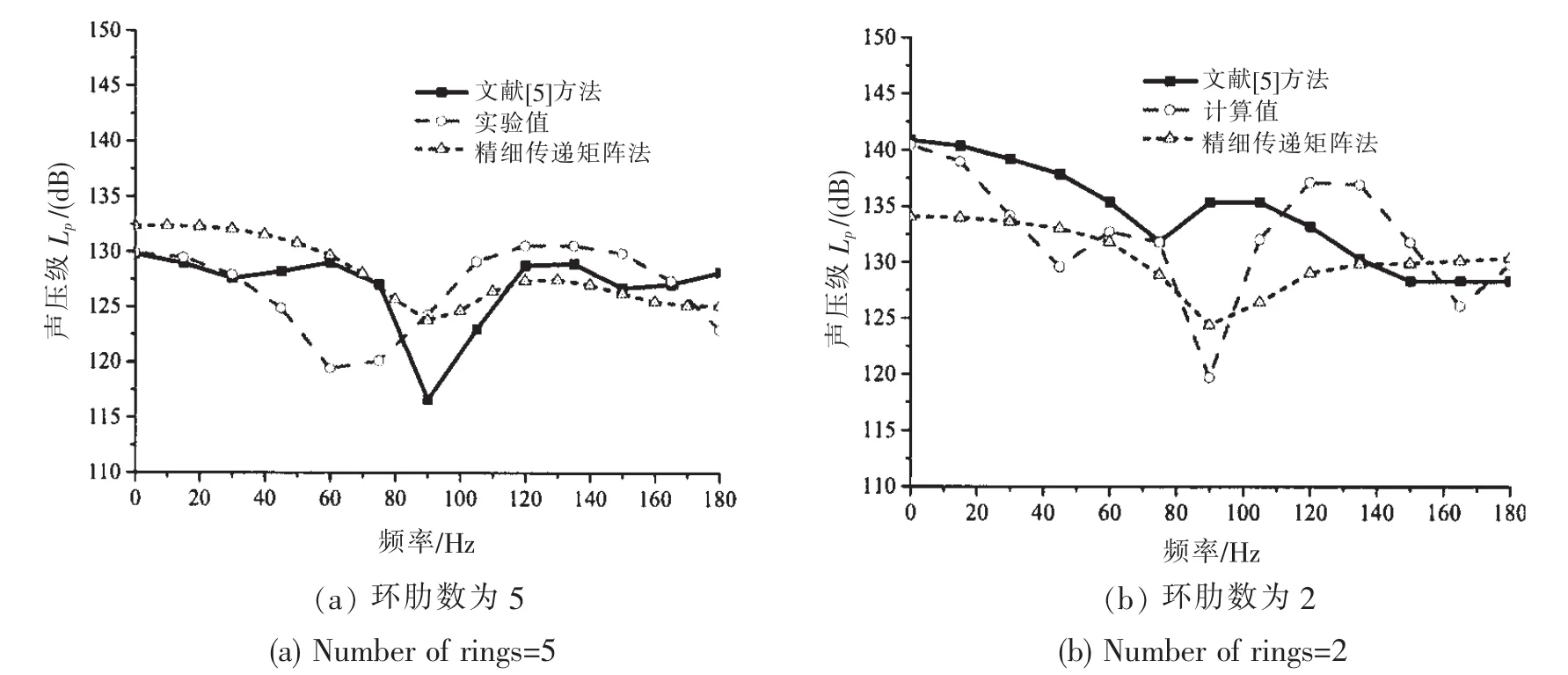
图4 环肋圆柱壳在f=4 kHz的计算结果对比曲线Fig.4 Comparison for the sound pressure resulted from precise transfer matrix method and test value

本文开展数值计算的圆柱壳模型主要参数如下：壳长L=0.6 m，半径R=0.2 m，厚度H=3 mm，柱壳的内肋为2 mm×30 mm，肋间距为0.20 m，径向激励力作用在内壳（L/2,0）处，幅值为1 N。测量点为（L/2,0,R+1 m），测量频率f=4 kHz。计算模型壳体，环肋材料相同，其弹性模量E=2e11N/m2，泊松比μ= 0.3，密度ρ=7 850 kg/m3，损耗因子η=0.01。流体的密度ρ0=1 000 kg/m3，声速度c0=1 500 m/s。边界条件为两端简支。分别讨论环肋，边界条件对水下声辐射的影响。

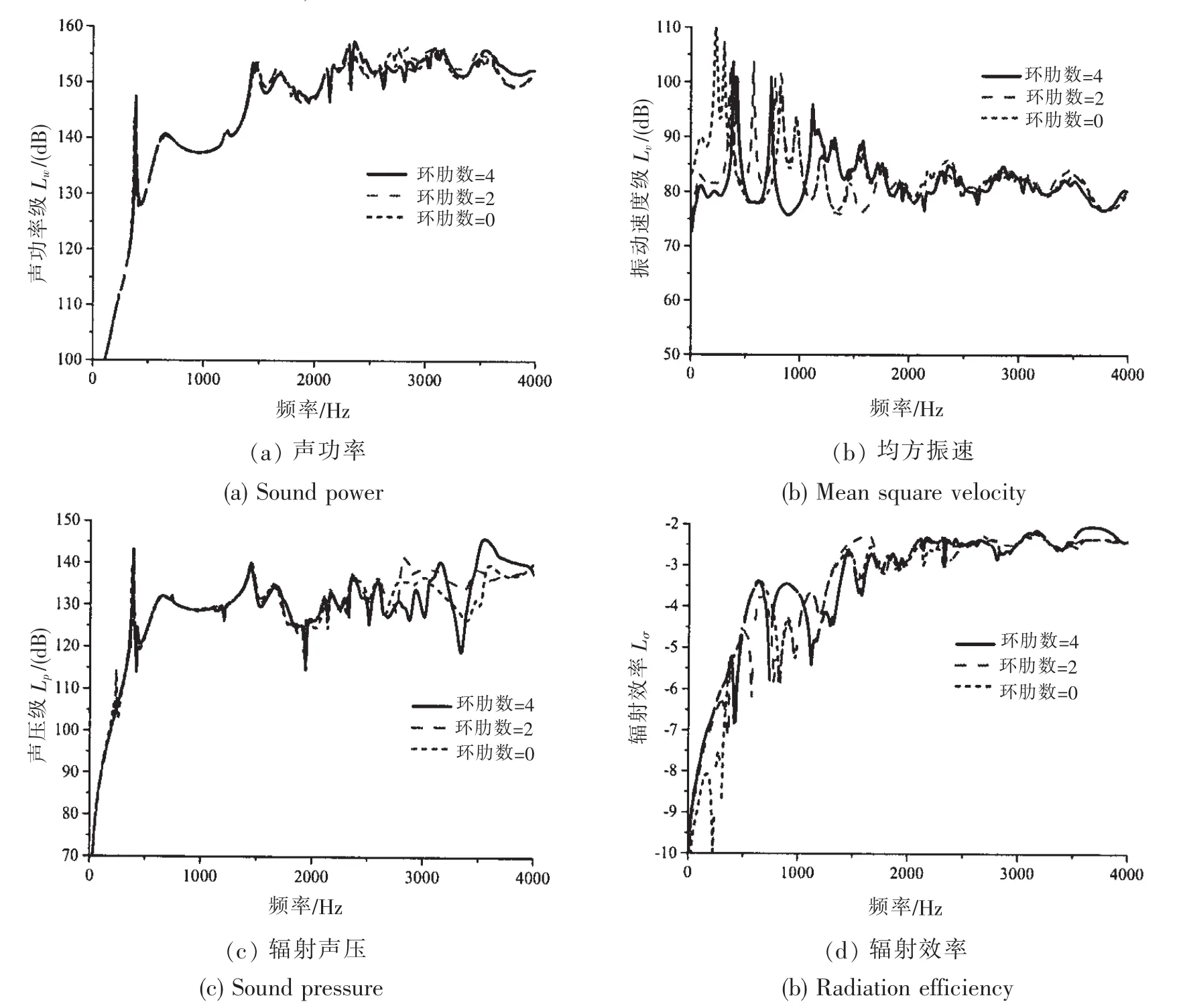
图5 环肋对加筋圆柱壳水下声辐射的影响Fig.5 Influence of ring ribs on the vibro-acoustic responses

从图5中可以看出，整体来看加肋前后对圆柱壳的辐射声功率平均趋势影响不大，特别是低频段0～1.5 kHz范围内，但在2.5 kHz以上频段，不同的环肋数目会导致辐射声压有不同程度的波动。从振动速度曲线可以看出，环肋会导致振动峰值的大小和位置有较大的偏移，同时环肋的存在会整体减低结构的振动速度。这是因为环肋的引入增加了圆柱壳的结构阻抗，低频时由于环肋与柱壳相比对结构阻抗增加不大，导致环肋对声辐射的影响较小。由于环肋改变了柱壳结构的振动速度，但对声辐射影响不大，这就必然会增加圆柱壳的辐射效率。

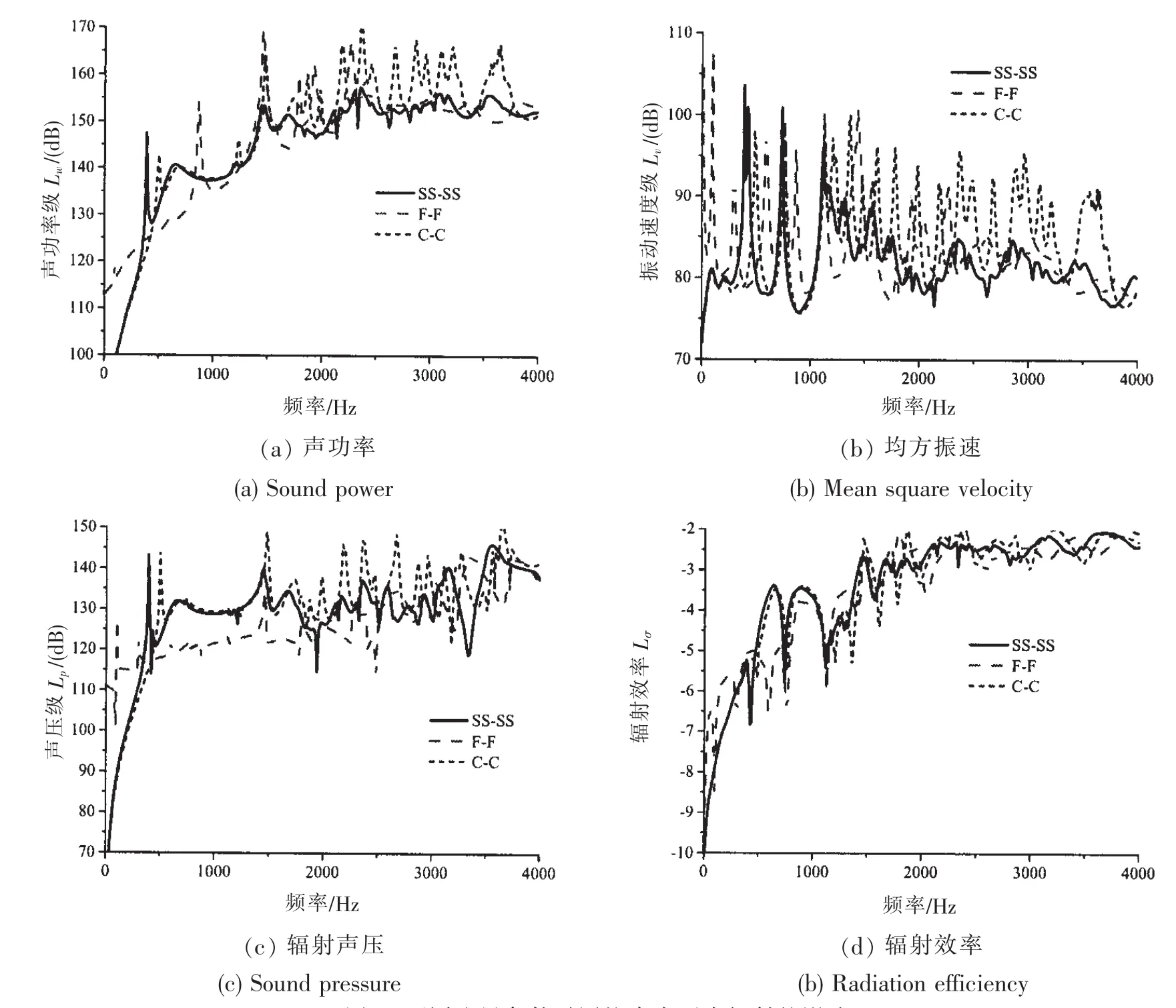
图6 不同边界条件对圆柱壳水下声辐射的影响Fig.6 Influence of boundary conditions on the vibro-acoustic responses

图6给出了两端简支、自由及固支边界条件的影响，从计算结果中可以看出，边界条件对圆柱壳的声辐射影响较大。整体来说，简支边界条件下的振动和声辐射相对较少。由于不同的边界条件改变了加筋圆柱壳的固有频率，导致结构振动速度曲线的峰值发生偏移。在0～500 Hz低频段自由边界条件不管振动速度还是声辐射都要比其它边界情况要大很多。在2～4 kHz频段两端固支情况时的声辐射声压与其它情况相比最大，其辐射效率与其它两种情况相比波动性较大。

4 结论

本文基于传递矩阵法，结合非齐次项的精细积分方法，建立了一种分析加筋圆柱壳声振响应的精细传递矩阵法。在针对本文方法的收敛性和有效性进行验证的基础上，讨论了环肋和边界条件对加筋圆柱壳声学特性的影响。结果表明，环肋对声辐射影响不大，但其改变了壳体的结构阻抗，会对结构的振动速度有一定影响，特别是峰值的位置和大小，同时增加了加筋圆柱壳的辐射效率。自由边界情况在低频时振动和声辐射均比较大，而在高频时固支边界的振动和声辐射与其它边界相比最大。

参考文献：

[1]Stepanishen P R.Modal coupling in the vibration of fluid-loaded cylindrical shells[J].The Journal of The Acoustical Society of America,1982,71：813-823.

[2]Sandman B E.Fluid-loaded influence coefficients for a finite cylindrical shell[J].The Journal of The Acoustical Society of America,1976,60：1256-1264.

[3]Harari A,Sandman B E.Radiation and vibrational properties of submerged stiffened cylindrical shells[J].The Journal of The Acoustical Society of America,1990,88：1817-1830.

[4]Laulagnet B,Guyader J L.Modal analysis of a shell’s acoustic radiation in light and heavy fluids[J].J Sound and Vibration,1989,131：397-415.

[5]Laulagnet B,Guyader J L.Sound radiation by finite cylindrical ring stiffened shells[J].J Sound and Vibration,1990,138：173-191.

[6]Totenham H,Shimizu K.Analysis of the free vibration of cantilever cylindrical thin elastic shells by the matrix progression method[J].International Journal of Mechanical Sciences,1972,14：293-310.

[7]Irie T.Free vibration of joined conical-cylinder shells[J].J Sound and Vibration,1984,95：31-39.

[8]Yamada G,Irie T,Tagawa Y.Free vibration of non-circular cylindrical shells with variable circumferential profile[J].J Sound and Vibration,1984,95：117-12.

[9]谭述君,高强,钟万勰.Duhamel项的精细积分方法在非线性微分方程数值求解中的应用[J].计算力学学报,2007, 27(5)：752-758. Tan Shujun,Gao Qiang,Zhong Wanxie.Applications of Duhamel term’s precise integration method in solving nonlinear differential equations[J].Chinese Journal of Computational Mechanics,2007,27(5)：752-758.

[10]钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994,34(2)：131-136. Zhong Wanxie.On precise time-integration method for structural dynamics[J].Journal of Dalian University of Technology, 1994,34(2)：131-136.

[11]Horner G C,Pilkey W D.The Riccati transfer matrix method[J].Journal of Mechanical Design ASME,1978,100：297-302.

[12]Pilkey W D,Chang P Y.Modern formulas for statics and dynamics[J].NewYork：McGraw-Hill Book Company,1978.

[13]Xiang Y,Yuan L Y,Huang Y Y,Ni Q.A novel matrix method for coupled vibration and damping effect analyses of liquid-filled circular cylindrical shells with partially constrained layer damping under harmonic excitation[J].Applied Mathematical Modelling,2011,35(5)：2209-2220.

[14]曹雷,马运义,黄玉盈.基于Riccati传递矩阵法分析水下有限长环肋圆柱壳的声辐射性能[J].振动与冲击,2009, 28(9)：149-154. Cao Lei,Ma Yunyi,Huang Yuying.Analysis of acoustic radiation of a ring-stiffened cylindrical shell with finite length in under water based on Riccati transfer matrix method[J].Journal of Vibration and Shock,2009,28(9)：149-154.

[15]陈美霞,骆东平,曹钢,蔡敏波.环肋柱壳振动和声辐射试验分析[J].华中科技大学学报,2003,31(4)：102-104. Chen Meixia,Luo Dongping,Cao Gang,Cai Minbo.Analysis of vibration and sound radiation from ring-stiffened cylindrical shell[J].Journal of Huazhong University of Science and Technology,2003,31(4)：102-104.

[16]汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1)：1-5. Tang Weilim,He Bingrong.Approximate from analytic solution of vibration and sound radiation stiffened finite cylindrical shells in water[J].Acta Acustica,2003,31(4)：102-104.

[17]李磊鑫,刘勇,陈炉云.焊接残余应力对环肋圆柱壳水下声辐射影响研究[J].船舶力学,2016,20(5)：628-634. Li Leixin,Liu Yong,Chen Luyun.Influence of welding-induced residual stress on underwater acoustic radiation of ring stiffened cylindrical shell[J].Journal of Ship Mechanics,2016,20(5)：628-634.

[18]Lin Changgang,Zou Mingsong,Jiao Huifeng,Liu Peng.Identification of non-stationary excitation and analysis of transient radiation noise on steering engine[J].Journal of Ship Mechanics,2016,20(6)：758-767.

Acoustic radiation of submerged ring-stiffened cylindrical shells with Precise Transfer Matrix Method

WANG Xian-zhong1,2,JIANG Chen-ban2,JI Fang3,FANG Yue-ming2
(1.Key Laboratory of High Performance Ship Technology(Wuhan University of Technology),Ministry of education, Wuhan 430063,China;2.Departments of Naval Architecture,Ocean and Structural Engineering,School of Transportation,Wuhan University of Technology,Wuhan 430063,China;3.China Ship Research And Development Academy,Beijing 100192,China)

Based on transfer matrix method,combined with precise integration method(PIM)of non-homogenous term,a Precise Transfer Matrix Method is developed for vibro-acoustic analysis of stiffened cylindrical shell.The field transfer matrixes and point transfer matrixes can be obtained from a set of the firstorder differential equations.The effects of generalized sound pressure can be considered by the techniques of increment storage and addition theorem.Then,the vibro-acoustic responses under point force excitation and sound pressure excitation can be solved by using continuous conditions on fluid solid interface.In addition,the convergence test of modes order is investigated.Results of the present method are also compared with model test results.The influences of ring ribs and boundary conditions on the vibro-acoustic responses are analyzed.

stiffener;cylindrical shell;sound radiation;precise transfer matrix method

TB53

A

10.3969/j.issn.1007-7294.2017.04.015

1007-7294（2017）04-0503-09

2016-10-13

国家自然科学基金（51409200，51409239）

王献忠（1986-），男，博士，副教授，E-mail：xianzhongwang00@163.com。