焊趾处椭圆表面裂纹的权函数与残余应力强度因子的权函数法

徐磊，黄小平

（上海交通大学海洋工程国家重点实验室，上海200240）

焊趾处椭圆表面裂纹的权函数与残余应力强度因子的权函数法

徐磊，黄小平

（上海交通大学海洋工程国家重点实验室，上海200240）

利用三维有限元计算了焊趾处半椭圆表面裂纹的应力强度因子。利用统一的权函数形式，结合得到裂纹半长比a/c=0.2；0.4；0.6；0.8，a/t=0.1～0.8的有限元数据，得到了适用于T型接头焊趾处半椭圆表面裂纹最深点和表面点的权函数。权函数的准确性，用有限元在裂纹面施加高阶载荷进行了验证，对于表面点和最深点，半长比a/c= 0.2～0.8，a/t=0.1～0.8，权函数与有限元结果误差在8%以下。基于得到的权函数，计算了T型接头焊趾处半椭圆表面裂纹的残余应力强度因子Kres，并与有限元计算结果进行对比，对比误差在10%以下，表明新的权函数能很好地预测T型接头焊趾处的残余应力强度因子。

T型接头；焊趾；表面裂纹；应力强度因子；权函数；残余应力

0 引言

工程结构中存在着大量的焊接接头，焊接接头焊趾处的半椭圆裂纹通常是该结构存在的最普遍的缺陷形式。计算这些结构物中出现裂纹以后，裂尖应力强度因子的大小，是损伤容限设计极其重要的一部分[1]。

对于平板含有椭圆表面裂纹应力强度因子的计算，已经有大量的学者对此进行了研究。其中认可度最广的是Raju与Newman[2]基于大量有限元数据得到的经验公式，英国最新的金属结构裂纹验收评定方法指南（BS7910）[3]便是以该公式为基础，提出了平板半椭圆裂纹应力强度因子的计算表达式。当裂纹存在于平板对接头，T型焊接头的焊趾处时，焊趾处的应力集中和焊趾复杂的几何模型就会使得计算应力强度因子变得相对困难。对于焊趾的处理，Bowness[4]在总结前人工作的基础上，结合三维有限元分析，给出了焊趾处应力强度因子的放大系数Mk的计算公式。

对于以上的经验公式，其使用范围均是在已知远场应力载荷形式的情况下得出的。实际结构中的载荷应力形式往往比已知的远场外载荷复杂得多，尤其是在焊趾处，通常的制造过程将在焊趾处引入很大的焊接残余应力。因此，怎么计算由残余应力引起的残余应力强度因子Kres，由此来评估残余应力对疲劳寿命的影响，变成了另外一个问题。因为已有的经验公式并不能适用于裂纹近场残余应力导致的应力强度因子的计算，学者Bao Rui[5]运用权函数计算了几种简单试件的残余应力强度因子，Labeas[6]给出了数值计算穿透裂纹的残余应力强度因子的方法。

利用权函数来计算应力强度因子，很好地解决了残余应力强度因子的计算问题。权函数法是求解在任意载荷分布下，尤其是裂纹处的应力场分布很复杂的情况下，计算裂纹应力强度因子具有十分高的效率。对于平板表面半椭圆裂纹的应力强度因子，Wang[7-8]通过对含有三维表面椭圆裂纹有限平板在线性载荷与抛物线载荷下进行了裂纹应力强度因子的计算，并结合Shiratori等人[9]的数据,在已有的统一权函数形式上，通过有限元计算，分别给出了平板裂纹小半长比（a/c＜1）和大半长比（a/c＞1）裂纹的权函数。本文将以求解平板权函数的思路，结合三维有限元裂纹分析的数据，提出一个适用于T型接头焊趾处表面裂纹的权函数，并用二次和三次应力分布验证了其有效性，基于得到的新权函数，计算T型接头焊趾处半椭圆表面裂纹的残余应力强度因子Kres，并与有限元计算结果进行对比。探讨权函数在残余应力强度因子计算中的适用性。

1 权函数的统一形式

Bueckner[10]和Rice[11]提出了任意载荷下，计算裂纹应力强度因子K的权函数法。其具体表达式为

式中：σ（x）为假想无裂纹体裂纹处应力分布，m（x,a）为权函数。

Glinka和Shen[12]指出，对于一维与二维的裂纹，权函数可有如下的统一形式

当运用到半椭圆的表面裂纹时，当x=a时表示为裂纹的最深点，当x=0时表示为裂纹的表面点，如图1所示。统一的权函数运用到半椭圆表面裂纹最深点时的计算公式如下：

图1 T型接头焊趾裂纹几何示意图Fig.1 T-butt weld toe crack geometry

统一的权函数运用到半椭圆表面裂纹表面点时的计算公式如下：

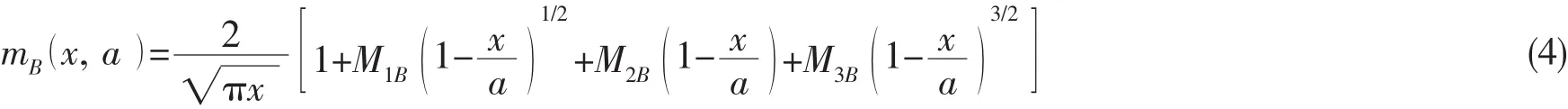
式中：M1A，M2A，M3A和M1B，M2B，M3B为对应于T型接头焊趾处的计算系数，可以通过在裂纹面施加常数和线性载荷，并结合推导裂纹权函数的自适应条件来求得。Glinka和Shen在推导权函数的统一形式时，指出x=a，即裂纹最深点权函数的自适应条件为：

x=0，即裂纹表面点权函数的自适应条件为

2 焊趾表面裂纹的权函数

2.1 有限元模型的建立

有限元计算模型为T型接头，长L=100 mm；宽W=100 mm；板厚H=10 mm；焊角θ=45°；焊趾宽度t=5 mm；翼板高度h=25 mm；杨氏模量E=2.1e5MPa；泊松比ν=0.3；椭圆裂纹长度为c，深度为a。具体如图1所示。

有限元在计算应力强度因子时，边界条件为固定四个顶点；载荷施加方式为直接施加在两个裂纹面上。有限元软件为ANSYS14.0；采用的单元为20节点的solid186高阶体单元，其中裂尖单元采用奇异单元处理。计算应力强度因子的方法为ANSYS自带的位移插值法。求得的SIF值采用如下公式进行无量纲化：

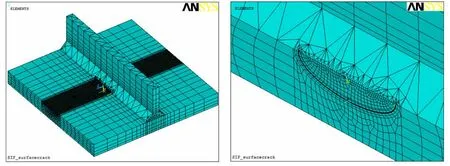
图2 T型接头焊趾处有限元模型Fig.2 T-butt weld toe crack FE model

2.2 裂纹最深点处的权函数

为了求得焊趾处裂纹最深点的权函数，即要求出（3）式中对应于T型接头的三个系数M1A，M2A， M3A。求解方法是，在裂纹面上分别直接施加常数载荷与线性载荷，并求得与之对应的最深点应力强度因子、，结合裂纹最深点权函数的自适应条件式（5），即可求得裂纹最深点的权函数。对于裂纹最深点处的应力强度因子，数值计算了半长比a/c=0.2；0.4；0.6；0.8，a/t=0.1～0.8之间的应力强度因子，给出了误差在5%以下的拟合公式。

常载荷下：

表1 T-butt SIF有限元结果σ（x）=σ0Tab.1 T-butt SIF FEM result σ（x）=σ0

续表1

图3 载荷σ（x）=σ0的SIF拟合曲面（左—表面点；右—最深点）Fig.3 SIF fitting curve when load σ（x）=σ0(left-surface point;right-deepest point)

2.3 裂纹表面点处的权函数

与求解最深点处的计算方法类似。在裂纹面上分别直接施加常数载荷σ（x）＝σ0与线性载荷并求得与之对应表面点的应力强度因子和，结合裂纹表面点权函数的自适应条件，等式（6），即可求得裂纹表面点的权函数。数值计算了半长比a/c=0.2；0.4；0.6；0.8，a/t=0.1～0.8之间裂纹表面点的应力强度因子，并给出了误差在5%以下的拟合公式。

常载荷下：

结果：

线性载荷下：

结果：

将（15）～（20）式代入（1）式，并结合裂纹表面点权函数的自适应条件式（6），求得对应于T型接头表面半椭圆裂纹最深点处权函数的计算系数为：

表2 T-butt SIF有限元结果σ（x）=σ0（1-x/a）Tab.2 T-butt SIF FEM result σ（x）=σ0（1-x/a）

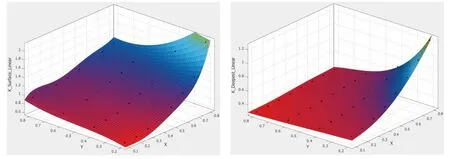
图4 载荷σ（x）=σ0（1-x/a）的SIF拟合曲面（左—表面点；右—最深点）Fig.4 SIF fitting curve when load σ（x）=σ0（1-x/a）,(left-surface point;right-deepest point)

3 权函数有效性的验证

在Glinka和Shen提出已有的统一权函数基础上，依据Wang求解平板权函数的思路，计算了裂纹半长比a/c=0.2；0.4；0.6；0.8，a/t=0.1～0.8之间的应力强度因子，得到了针对T型接头焊趾处，计算

表面半椭圆裂纹应力强度因子的权函数。为了验证该权函数的有效性，将一阶与二价载荷下得到的权函数扩展到高阶载荷的情形，权函数计算得到的高阶载荷下裂纹应力强度因子与FEA结果进行对比。验证的思路为：若该权函数能够在已知裂纹处近场应力σ（）x的分布情况下，能准确地计算裂纹处的应力强度因子，那么T型接头裂纹面在高阶载荷的作用下FEA得到的SIF，应与得到的权函数计算的SIF的计算值有很好的吻合。

表3 T-butt SIF有限元结果_二次载荷σ（x）=σ0（1-x/a）2Tab.3 T-butt SIF FEM result_parabolic load σ（x）=σ0（1-x/a）2

表4 T-butt SIF有限元结果_三次载荷σ（x）=σ0（1-x/a）3Tab.4 T-butt SIF FEM result_Cubic load σ（x）=σ0（1-x/a）3

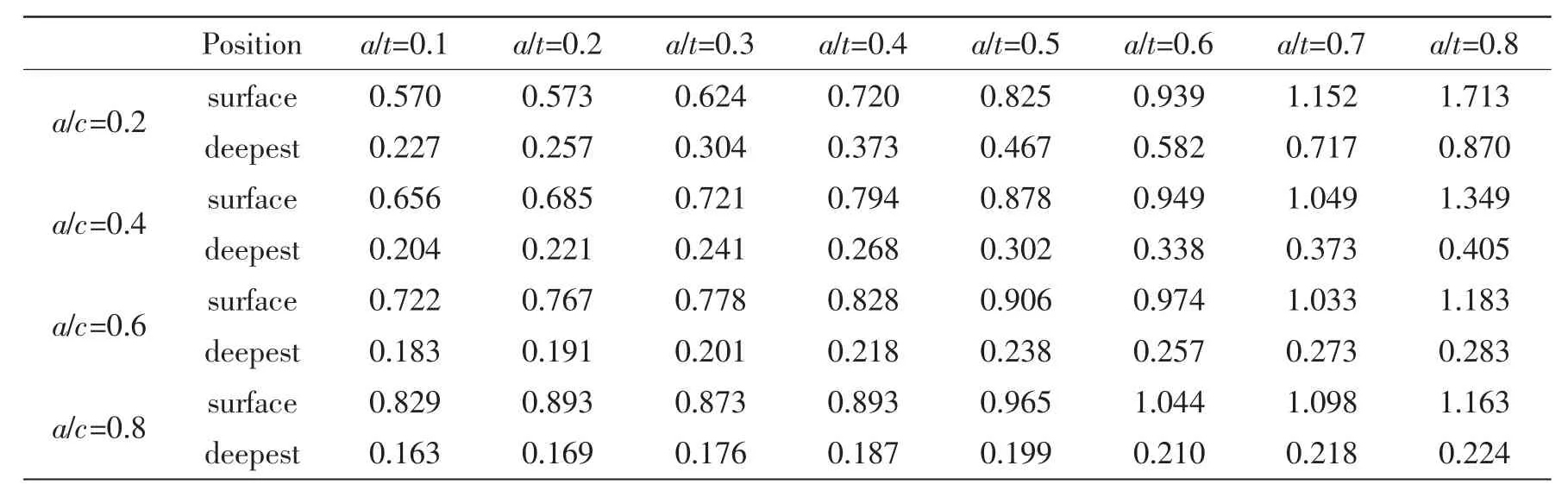
表5 T-butt SIF权函数结果_二次载荷σ（x）=σ0（1-x/a）2Tab.5 T-butt SIF WFM result_parabolic load σ（x）=σ0（1-x/a）2

表6 T-butt SIF权函数结果_三次载荷σ（x）=σ0（1-x/a）3Tab.6 T-butt SIF WFM result_Cubic load σ（x）=σ0（1-x/a）3

焊趾处表面裂纹高阶载荷作用下FEA得到的SIF与权函数对比结果：

图5所示，二次载荷作用下表面点SIF，在裂纹半长比a/c=0.2～0.8时，a/t= 0.1～0.8时，权函数法与FEA得到的结果，两者之间差值的百分比最大值在a/c=0.6，a/t=0.6处取得为6.3%，在a/c=0.6，a/t=0.4处，二者差值也达到6.1%；其余点，二者之间差值的百分比均在5%以下。

图6所示，二次载荷作用下最深点SIF，在裂纹半长比a/c=0.2～0.8时，a/t= 0.1～0.8时，权函数法与FEA得到的结果，两者之间差值的百分比最大值在a/c=0.4，a/t=0.8处取得为14.3%，在a/c=0.2，a/t=0.3处，二者差值也达到5.2%；其余点，二者之间差值的百分比均在5%以下。

图7所示，三次载荷作用下表面点SIF，在裂纹半长比a/c=0.2～0.8时，a/t= 0.1～0.8时，权函数法与FEA得到的结果，两者之间差值的百分比最大值在a/c=0.4，a/t=0.6处取得为16.4%，在a/c=0.6，a/t=0.4处，二者差值也达到8%；其余点，二者之间差值的百分比均在5%以下。

图8所示，三次载荷作用下最深点SIF，在裂纹半长比a/c=0.2～0.8时，a/t=0.1～0.8时，权函数法与FEA得到的结果，两者之间差值的百分比最大值在a/c=0.4，a/t= 0.8处取得为10.6%，其中在a/c=0.8，a/t= 0.1，二者差值也达到9.3%；其余点，二者之间差值的百分比均在8%以下。

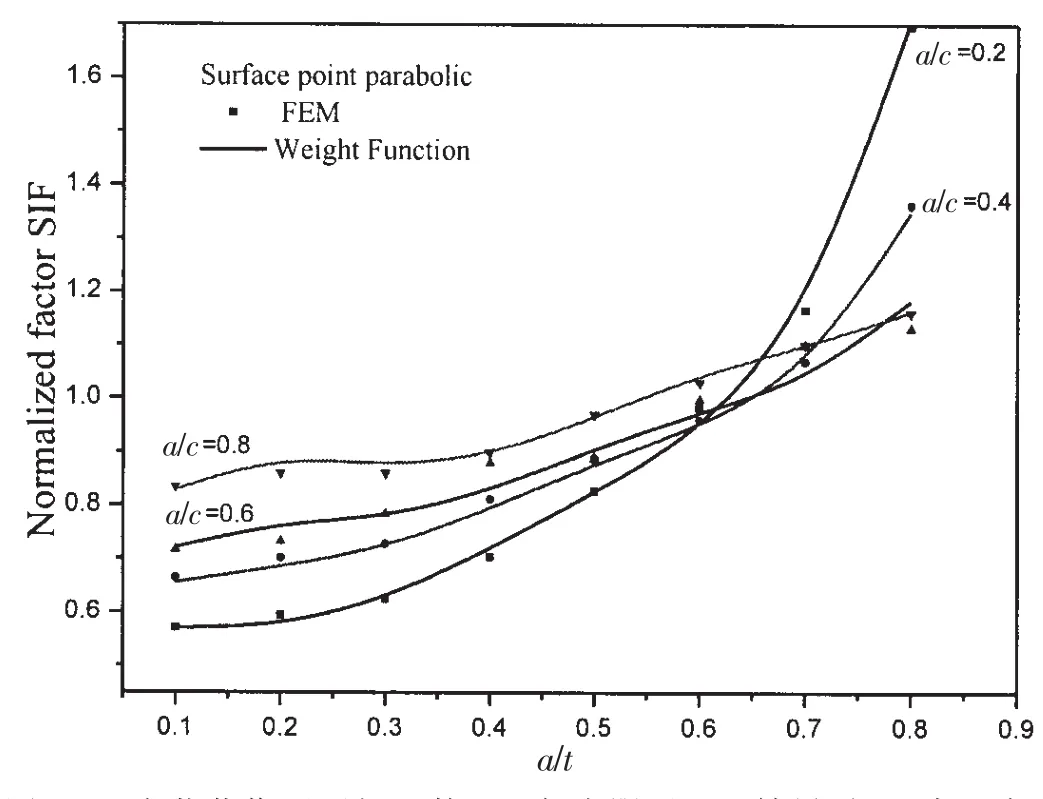
图5 二次载荷作用下权函数SIF与有限元SIF结果对比（表面点）Fig.5 Comparison between weight function result and FEM result for parabolic stress distribution(Surface point)

图6 二次载荷作用下权函数SIF与有限元SIF结果对比（最深点）Fig.6 Comparison between weight function result and FEM result for parabolic stress distribution(Deepest point)

图7 三次载荷作用下权函数SIF与有限元SIF结果对比（表面点）Fig.7 Comparison between weight function result and FEM result for cubic stress distribution(Surface point)

4 焊趾处半椭圆表面残余应力强度因子Kres的权函数法

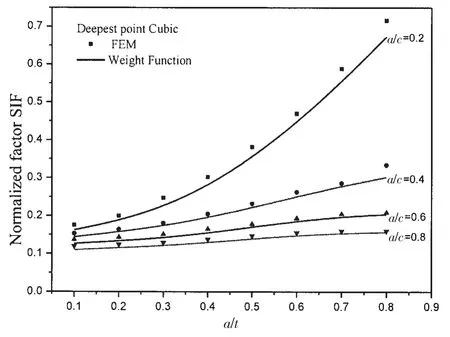
图8 三次载荷作用下权函数SIF与有限元SIF结果对比（最深点）Fig.8 Comparison between weight function result and FEM result for cubic stress distribution(Deepest point)

4.1 焊接残余应力的分布

采用权函数法计算应力强度因子，必须知道焊趾处垂直于裂纹面上沿板厚度的方向的应力分布。在过去的研究中，对于残余应力场中的应力强度因子计算，由于残余应力分布的复杂，通常采用已有的残余应力分布经验公式。

文献[13]提出在钢材焊接后的焊趾表面处的残余应力大小为

式中：σR表示残余应力，σy表示材料的屈服极限。

在此基础上，文献[14]给出了厚板多道焊接后，残余应力沿着板厚度方向上的分布，其简化形式为如下：

但是实际过程中，焊接后残余应力的分布是十分复杂的，焊趾处残余应力沿板厚度方向上的分布与板厚，焊接时线热量的输入都有十分密切的关系。为了得到更加准确的结果，对T型接头进行焊接过程的模拟。弹性模量E=2.1×105MPa，泊松比ν=0.3，σy=235 MPa。其它热力学的参数参考文献[10]。

图9 T型接头焊接后的典型残余应力场Fig.9 T-butt residual stress distribution

4.2 焊趾处垂直裂纹面残余应力的确定

由图10可以看到T型接头焊接后沿着焊缝方向的残余应力场，纵向残余应力和横向残余应力由板的两端向中间的过程中，有一个上升和下降的趋势，而在板的中间处，纵向残余应力与横向残余应力随着离起焊点距离S而变化，但其变化趋势不大，故而为了得到简化的沿板厚方向垂直于裂纹面的横向残余应力，我们可以假设：在焊趾处裂纹的位置，沿着焊缝方向裂纹面上的横向残余应力不变，只需要提取出焊趾处椭圆裂纹处沿着厚度方向上横向残余应力σ（）x。

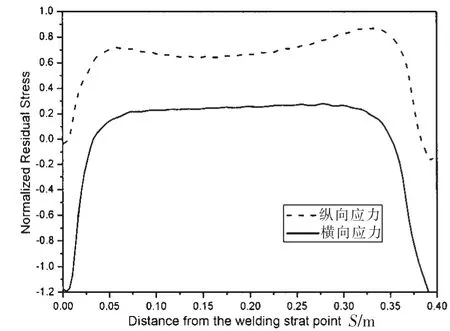
图10 沿焊缝方向残余应力分布Fig.10 Residual stress distribution along welding direction

图11 焊趾处残余应力沿板厚分布拟合曲线Fig.11 T-butt residual stress fit curve

图11所示为T型头底板厚度t=10 mm焊接后，提取的沿厚度方向上垂直于裂纹面横向残余应力的散点分布图。对于提取出来的残余应力离散点，采用多项式拟合后，得到了残余应力沿厚度方向的分布函数，（24）式。沿厚度方向上的残余应力分布确定后，结合T型接头半椭圆裂纹的权函数，则可求出T型接头裂纹最深点与表面点的应力强度因子。

5 Kres结果讨论

对T型接头焊趾处半椭圆表面裂纹在残余应力场中的应力强度因子Kres，分别采用了权函数法和有限元法进行计算。其中，导出的T型接头焊趾处半椭圆裂纹表面裂纹权函数的准确性用高次应力载荷进行了验证，结果与有限元法相比，其求解误差大体在8%以下。在此基础上，验证该权函数计算残余应力强度因子Kres的准确性，并与有限元结果进行对比。T型接头焊趾处裂纹在（24）式所示的残余应力）作用下，分别用权函数法与有限元法计算在不同裂纹尺寸a/c=0.2；a/c=0.4；a/c=0.6；a/c=0.8，a/t=0.1～0.8下的残余应力强度因子Kres，计算结果无量纲化后如表7和表8所示。

无量纲化后的结果对比如图12所示。

图12所示，在裂纹半长比a/c=0.2时，a/t=0.1～0.8时，权函数法与有限元法得到的最深点Kres最大差值的百分比在a/t=0.8时取得为6.2%，其余点差值均在5%以下。在a/c=0.2时，权函数法与有限元法得到的表面点Kres，两者之间差值的百分比最大值在a/t=0.6处取得为3.8%，其余各点差值均在3%以下。

表7 半椭圆表面裂纹Kres_有限元法（a/c=0.2；a/c=0.4；a/c=0.6；a/c=0.8）Tab.7 Kresof semi-elliptical crack by FEA method

表8 半椭圆表面裂纹Kres_权函数法（a/c=0.2；a/c=0.4；a/c=0.6；a/c=0.8）Tab.8 Kresof semi-elliptical crack by weight function method

图12 权函数法与有限元法Kres对比Fig.12 Comparison of Kresbetween FEA and WFM

在裂纹半长比a/c=0.4时，a/t=0.1～0.8时，权函数法与有限元法得到的最深点Kres最大差值的百分比在a/t=0.8时取得为9.2%，其余点差值均在3%以下。在a/c=0.2时，权函数法与有限元法得到的表面点Kres，两者之间差值的百分比最大值在a/t=0.2处取得为2.5%，其余各点差值均在2%以下。

在裂纹半长比a/c=0.6时，a/t=0.1～0.8时，权函数法与有限元法得到的最深点Kres最大差值的百分比在a/t=0.5时取得为8.4%，其余点差值均在4%以下。在a/c=0.6时，权函数法与有限元法得到的表面点Kres，两者之间差值的百分比最大值在a/t=0.7处取得为5.3%，其余各点差值均在5%以下。

在裂纹半长比a/c=0.8时，a/t=0.1～0.8时，权函数法与有限元法得到的最深点Kres最大差值的百分比在a/t=0.7时取得为3.6%，其余点差值均在3%以下。在a/c=0.6时，权函数法与有限元法得到的表面点Kres，两者之间差值的百分比最大值在a/t=0.3处取得为8.3%，其余各点差值均在2%以下。

6 结论

本文在已有的权函数统一形式上，用三维有限元计算得到了焊趾处a/c=0.2；0.4；0.6；0.8，a/t=0.1～0.8之间裂纹最深点与表面点的应力强度因子，得到以下结果：

（1）利用已有的权函数统一形式，结合T型接头焊趾处半椭圆裂纹最深点与表面点的三维有限元计算数据，得出了适用于焊趾表面半椭圆裂纹最深点和表面点的权函数。

（2）权函数的准确性，扩展到了二次和三次应力分布下。对于表面点，半长比a/c=0.2～0.8，a/t=0.2～0.8之间，权函数与FEA结果误差几乎均在8%以下；对于最深点，半长比a/c=0.2～0.8，a/t=0.1～0.8之间，权函数与FEA结果误差均在在8%以下。权函数的准确性在这儿得到了有效验证。

（3）基于新的权函数，对T型接头焊趾处半椭圆表面裂纹的残余应力强度因子Kres进行了计算，并与有限元计算结果进行对比，对比误差在10%以下，表明新的权函数能很好地预测T型接头焊趾处的残余应力强度因子Kres。

[1]Servetti G,Zhang X.Predicting fatigue crack growth rate in a welded butt joint：The role of effective R ratio in accounting for residual stress effect[J].Engineering Fracture Mechanics,2009,76(11)：1589-1602.

[2]Newman Jr J C,Raju I S.An empirical stress-intensity factor equation for the surface crack[J].Engineering Fracture Mechanics,1981,15(1)：185-192.

[3]Standard B.7910：1999：Guide on methods for assessing the acceptability of flaws in fusion welded structures[J].British Standard Institution,2000.

[4]Bowness D,Lee M M K.Prediction of weld toe magnification factors for semi-elliptical cracks in T-butt joints[J].International Journal of Fatigue,2000,22(5)：369-387.

[5]Bao R,Zhang X,Yahaya N A.Evaluating stress intensity factors due to weld residual stresses by the weight function and finite element methods[J].Engineering Fracture Mechanics,2010,77(13)：2550-2566.

[6]Labeas G,Diamantakos I.Numerical investigation of through crack behavior under welding residual stresses[J].Engineering Fracture Mechanics,2009,76(11)：1691-1702.

[7]Wang X,Lambert S B.Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite-thickness plates subjected to nonuniform stresses[J].Engineering Fracture Mechanics,1995,51(4)：517-532.

[8]Wang X,Lambert S B.Stress intensity factors and weight functions for high aspect ratio semi-elliptical surface cracks in finite-thickness plates[J].Engineering Fracture Mechanics,1997,57(1)：13-24.

[9]Shiratori M.Analysis of stress intensity factors for surface cracks subjected to arbitrarily distributed surface stresses[J].Transaction of JSME(Series A),1987,54(467)：1828-1835.

[10]Bueckner H F.Novel principle for the computation of stress intensity factors[J].Zeitschrift fuer Angewandte Mathematik& Mechanik,1970,50(9).

[11]Rice J R.Some remarks on elastic crack-tip stress fields[J].International Journal of Solids and Structures,1972,8(6)：751-758.

[12]Glinka G,Shen G.Universal features of weight functions for cracks in mode I[J].Engineering Fracture Mechanics,1991, 40(6)：1135-1146.

[13]黄小平,贾贵磊,崔维成,祈恩荣.海洋钢结构疲劳裂纹扩展预报单一扩展率曲线模型[J].船舶力学,2011,15(1-2)：118-125. Huang Xiaoping,Jia Guilei,Cui Weicheng.Unique crack growth rate curve model for fatigue life prediction of marine steel structures[J].Journal of Ship Mechanics,2011,15(1-2)：118-125.

[14]Miki C,Mori T,Tajima J.Effect of stress ratio and tensile residual stress on near threshold fatigue crack growth[C]//Proceedings of JSCE,1986(368)：187-193.

[15]颜鸣皋,等.航空材料手册[M].北京：中国标准出版社,2002：104-131.

Weight function for weld toe semi-elliptical surface crack and calculating residual stress intensity factors by weight function method

XÜ Lei,HUANG Xiao-ping
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

The stress intensity factors(SIFs)of semi-elliptical surface cracks at the weld toe were analyzed by using finite element analysis(FEA).Based on the obtained stress intensity factor data of surface cracks with aspect ratio from a/c=0.2～0.8 and a/t=0.1～0.8 by FEA,new weight functions for the calculation of T-butt weld toe surface cracks SIFs at both surface and deepest point were derived under constant and linear distributed stresses.The new weight functions were extended for higher order stress distribution situation and validated through the results obtained by FEA under parabolic and cubic stress loading.The difference between weight function and FEA is less than 10%for cracks with aspect ratio a/c=0.2～0.8,a/t= 0.1～0.8 at both surface point and deepest point.The derived weight function is used to calculate the SIFs of weld toe surface crack due to residual stress,results comparison with FEA method shows new weight function can make good predication for the weld toe surface crack SIFs.

T-butt;weld toe;surface crack;stress intensity factor;weight function;residual stress

U661.4

A

10.3969/j.issn.1007-7294.2017.04.009

1007-7294（2017）04-0443-12

2016-12-27

徐磊（1989-），男，硕士生；黄小平（1963-），男，副教授，通讯作者，E-mail：xphuang@sjtu.edu.cn。