生长进化拓扑优化算法在油船中剖面结构优化上的运用
刘宏亮,夏利娟,吴嘉蒙
(1.上海交通大学海洋工程国家重点实验室,上海200240;2.中国船舶及海洋工程设计研究院,上海200011)
生长进化拓扑优化算法在油船中剖面结构优化上的运用
刘宏亮1,夏利娟1,吴嘉蒙2
(1.上海交通大学海洋工程国家重点实验室,上海200240;2.中国船舶及海洋工程设计研究院,上海200011)
单元进化生长拓扑优化算法较之其他拓扑优化算法有其独特之处,文章通过引入单元生长进化算法对VLCC中剖面横撑结构进行优化设计。结合单元应力指标函数及单元权重系数确定优化模型的目标函数,通过计算单元应力确定单元权重系数的迭代递推关系式,结合有限元平衡方程建立优化数学模型,通过解析计算知优化模型目标函数的取值主要取决于体积函数值,依此建立完整的单元生长进化优化流程。通过与ANSYS连续体拓扑优化计算的比较可知单元生长进化算法更加简单高效,对VLCC轻量化设计具有一定的理论参考价值。
单元生长进化算法;拓扑优化;应力指标函数;VLCC中剖面优化
0 引言
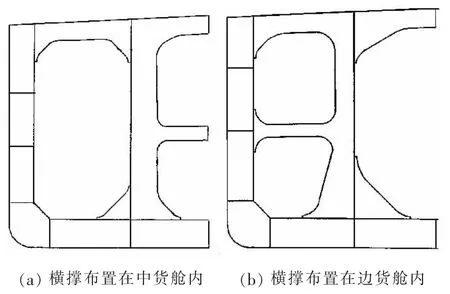
图1 VLCC典型的横撑布置Fig.1 Typical VLCC’s transverse brace arrangement
目前,我国设计和建造的油船与国外同类型船相比还是存在一定差距,主要反映在空船重量偏高、油耗偏高、建造效率偏低等,其中空船重量的差异直接影响了诸如油耗、建造成本、船舶能效设计指数(EEDI)等指标。具体地说,目前国内建造的32万吨VLCC的平均空船重量约为46 500吨,而韩国建造的同尺度VLCC的平均空船重量仅为44 500吨左右。因此,有必要运用结构优化设计方法,改进现有的油船结构设计,以取得更好的经济效益。
横撑结构是VLCC特有的结构构件,如图1所示,其主要作用是支撑油船纵舱壁上的垂直桁结构,可布置在中货舱和边货油舱。目前,30万吨级VLCC结构中1根横撑的结构重量约为14吨左右,而整个货舱区的横撑数量为25~35根,如能取消横撑,预估将减轻约200吨左右的结构重量,因此,有必要对横撑的中剖面结构进行优化研究。
对于单元生长进化拓扑优化国内外很多学者取得了很多新的研究进展。刘远东等[1]运用单元生长进化方法对圆形阻尼层合板的阻尼特性进行优化设计,以阻尼材料用量为约束条件,以提高阻尼层的利用率为目标,找到了圆形阻尼层合板的拓扑优化构型,并用相关实验验证了优化设计的准确性;王仁华、Chan和Kaveh等[2-6]将智能算法形状退火算法运用到结构拓扑优化设计中,通过与其他拓扑优化方法的比较验证了该方法的可行性;何林伟、Amstutz等[7-8]基于基结构,通过比较前后两次结构单元的性能指标来增加和删除单元,提供了一种类似单元生长进化方法的连续体结构拓扑优化的简单实现;张宇、Lotfi等[9-10]基于SIMP插值模型,给出了一种基于ANSYS的滤波控制算法,通过具体的数值算例验证了方法的可行性;胡兴国、Rong等[11-12]改进了传统的结构进化优化算法,提出每次删除的单元数量根据保留单元数成固定比例,提高了进化优化的效率;王雷等[13]运用仿生优化方法,增加承载力大区域的材料,减小承载小区域的材料,提出了一种连续体结构拓扑优化的新方法;左中杰、Huang、Xie等[14-15]运用ANSYS的单元生死技术给出了一种基于渐进结构优化方法的拱坝结构曲线函数优化。
上述研究提出了很多新思路,进一步完善了结构拓扑优化理论体系。因此,本文根据渐进式单元生长算法,结合有限元以及变密度SIMP拓扑优化理论,建立较完整的VLCC中剖面横撑结构拓扑优化模型。将优化结果与ANSYS连续体优化准则拓扑优化结果进行对比,验证了算法的有效性,并且提出了一种减轻VLCC空船重量的可行设计思路,对工程实际具有一定的理论参考价值。
1 考虑应力指标函数的单元生长拓扑优化数学模型
拓扑优化算法很难提供解析的数学优化模型,常用的变密度理论如SIMP法是将离散的单元变量通过相应的假设转变为单元材料属性(如单元刚度、材料密度)的连续变量问题,从而能够建立初步的数学模型,并进行近似的解析数学优化计算。单元生长进化算法是通过寻找结构最优传力路径,通过在迭代计算中增加或删除单元从而获得最优的结构拓扑构型。它是建立在单元有限元计算基础上的结构智能生长优化模式,因此可以从有限元分析如刚度矩阵的求解和等效平衡方程的建立出发,通过相应的数学解析计算建立具体的拓扑优化数学模型。
1.1 优化模型自变量参数的确定
单元生长进化算法在迭代的初始要确立简单的结构初始构型以及相应载荷边界条件,在优化迭代计算过程中,寻找结构的最优传力路径,通过在应力较大的单元周围产生新单元,删除应力较小的单元来获得拓扑构型。因此,单元生长进化算法需建立前后的迭代关系:

判断单元的生长和删除要考虑单元的应力水平,但是不能直接以单元的应力值作为单元生长和删除的标准,因为单元应力值是迭代计算后得到的结果,并且结构的应力水平会随着结构的拓扑生长发生很大变化,因此,建立单元的权重系数xi(i=0,1,2L n)并以此为标准判断单元的增减,单元权重系数值在每一次迭代计算中都会随单元的应力水平而变化,设定两个临界值判断迭代计算中单元的增减:
xi≤0.01;表示单元权重太小,单元承载较小,应该删除该单元。
0.01 ≤xi≤1;表示单元有一定承载,继续保留该单元。
xi>1;表示单元承载较大,单元权重大,应该在该单元周围产生新的单元,单元的生长示意图如图2[16]所示。
另一方面,结合SIMP变密度函数方法,单元的材料属性跟单元权重系数满足如下迭代关系式:


图2 单元生长示意图(根据文献[16])Fig.2 Element growth diagram based on the reference[16]
式中:ρ0,E0是初始的材料密度和弹性模量,xi为单元在第i次迭代计算中的单元权重系数值。
因此,单元的权重系数大小决定单元的材料属性,并且有一个确定的临界值确定单元的增减,以此为优化模型的自变量函数能简化模型的迭代计算。
1.2 优化模型目标函数的确定
油船中剖面横撑结构优化设计模型中,主要考虑在结构应力的许可范围内减轻结构的重量;主要考虑两个方面:拓扑结构的Von Mises应力、拓扑结构的重量m。对于结构的相当应力,只要结构的应力水平在一个合理范围内就可接受,并不要求应力最小。另外,还需要考虑结构拓扑构型总体的应力水平,所以应该根据拓扑构型的最大单元应力σmax以及拓扑构型的平均单元应力σmean来确定一个应力水平指标函数,结构拓扑构型受力均匀程度可以用单元最大相当应力和平均单元相当应力的差值来衡量,所以,建立以下的应力水平指标函数:

式中:a、b是权重系数,且a+b=1;分别对应单元应力均匀程度以及最大的单元应力。在油船中剖面横撑结构优化设计模型中,a、b都取为0.5。
上述应力水平指标函数同时考虑了结构的受力均匀程度和结构最大应力,较好的拓扑构型应该有较优的结构传力路径且结构的最大应力在合理的范围内,要求有较小的最大单元应力及较小的应力差值,所以一个较好的拓扑构型应该有较小的结构应力水平指标函数。
考虑优化目标的另一个方面结构重量m,原则上油船中剖面横撑结构优化设计最直接的目标是使得纵舱壁支撑结构重量最小,但是结构的应力水平指标函数不能太大,设定结构的理想应力指标函数值为因此可以确定结构拓扑优化的目标函数:所以最终优化模型的目标函数为:

结合有限元计算平衡方程,同时设定应力指标函数所允许的最大值,油船中剖面横撑结构拓扑优化的数学模型如下所示:

2 优化数学模型的解析分析
油船中剖面横撑结构的拓扑优化模型中用到平面四边形单元计算,根据平面四边形单元的有限元计算理论,平面四边形单元的刚度矩阵:

根据(6)式可知,油船中剖面横撑结构的单元生长进化优化模型的目标函数仅仅随结构的密度函数和体积函数而改变。考虑到模型中的密度函数基本保持不变,所以优化目标即为保持单元应力水平指标函数值在允许的范围内让结构的体积最小,也就是结构重量最轻,也就是说在单元的生长和进化过程中尽量删除掉承载较小的单元。
3 具体的单元生长进化流程
单元生长进化算法的核心过程是单元随着迭代进程增加或删除,单元生长基于单元权重系数值的变化,所以(1)式所示的单元生长递推关系就等同于单元权重系数的递推关系式。根据前述对优化数学模型的解析计算分析可知,优化目标函数大小由结构拓扑构型的体积函数V()x决定,因此,通过寻找结构最优的传力路径,尽可能使单元受力均匀,减小承载较小的单元数目是得到最优解的必然条件。根据拓扑结构单元的平均应力σmean设定三个应力区间来建立单元权重函数的递推关系式,三个应力区间如下:(0,λσmean),[λσmean,σmean),[σmean,σmax),系数λ是设计参数,在油船中剖面横撑结构的优化模型中,λ=0.3,因此单元权重的递推关系式如下式所示:

根据拓扑构型的单元应力计算值,当单元应力值在缩减区间(0,λσmean),单元的权重系数值减小,直到减小到0.01,删除该单元;单元应力值在平衡区间[λσmean,σmean),单元权重系数值保持不变,单元受力均匀;单元应力值在生长区间[σmean,σmax),单元权重系数将增加,直到增加到1,在单元周围按图2所示增加新单元,新单元的权重系数取为1,并且原单元的单元权重系数减小为1。因此,形成新的拓扑构型,并在此基础上进行下一次的迭代计算。
根据单元生长计算的迭代关系可以确定迭代的终止条件,在单元的生长进化过程中伴随着单元的增加或删除,并且在每次迭代过程都会有单元的增加或删除;另一方面,优化模型的目标函数要求模型单元数最小,所以确定单元生长迭代的终止条件为:在N次迭代计算中,优化模型的目标函数仅在微小的范围内变动。N的确定由具体的模型确定,油船中剖面横撑结构的优化模型中N取为3。
至此,建立了完整的单元生长进化拓扑优化算法,优化流程图如图3所示。

图3 优化流程图Fig.3 The optimization flow chart
4 VLCC中剖面横撑结构拓扑优化
首先,确定拓扑优化设计的边界条件和载荷,VLCC纵舱壁是船体纵向主要构件,垂向连接船体主甲板和船体内底板与底纵桁,因此在单元生长进化拓扑优化模型中定义结构的边界为简支约束。VLCC纵舱壁承载的极限状态为一边货舱满载,一边空载,载荷示意图如图4所示。

图4 拓扑优化模型初始构型Fig.4 The initial configuration of the optimization model
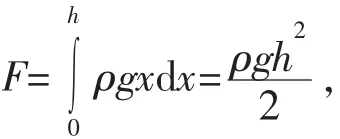
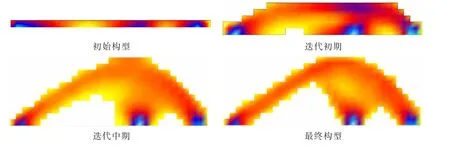
图5 单元生长进化优化结果示意图Fig.5 The result from the evolutionary structural optimization
从优化结果可知,在迭代初期,在初始构型基础上,根据响应的边界条件和载荷工况,拓扑构型产生大量新单元形成较完整的初始拓扑构型,单元数量增加明显即拓扑构型的重量增加;进入迭代中期阶段,根据拓扑优化目标函数设定,对新生成的拓扑构型进行优化计算,在满足优化约束条件的基础上,使优化模型的目标函数最小,即增加新单元的同时更注重寻找结构最优的传力路径,删除应力较小的单元,使结构拓扑构型的单元数量尽可能减少;最后通过进一步优化计算得到最终的拓扑优化构型。
为了验证单元生长拓扑优化算法在VLCC中剖面横撑结构优化设计中的有效性,将基于ANSYS平台的连续结构拓扑优化运用到VLCC中剖面横撑结构的拓扑优化过程中;ANSYS拓扑优化算法采用优化准则法,优化目标函数为结构构型的柔度,以最小柔度即结构最大刚度为目标,优化模型如下:

式中:Uc为结构变性能。
优化结果如图6所示。
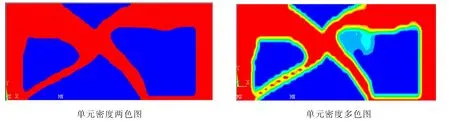
图6 ANSYS拓扑优化结果示意图Fig.6 The result from the ANSYS topology optimization
对比图5和图6两种方法的优化结果示意图可知,单元生长进化拓扑优化算法所得的最终优化拓扑构型更加清晰简单,通过寻找最优的结构传力路径,在应力较大单元周围生成新单元,删除应力较小的单元,得到的拓扑构型形状清晰简单。基于ANSYS平台的连续结构拓扑优化能控制结构的总体积,但是结构的拓扑构型辅助结构较多,构型较复杂。因此总体上讲,单元生长进化拓扑优化算法在VLCC中剖面横撑结构的优化上更加简单和有效,更加符合实际的优化设计。
因此根据图5最终的拓扑构型,VLCC纵舱壁支撑结构的横撑可以取消,只需加靠近船底的扶强材尺寸,具体的可行方案如图7所示。

图7 VLCC中剖面横撑取消优化设计图Fig.7 The VLCC mid-section optimal design by excluding the transverse brace
5 结语
自1992年Xie和Steven提出了进化结构优化算法(ESO)[16]以来,单元生长进化方法受到了广大学者的关注,其拓扑优化的简单高效性使其得到越来越广泛的运用。文章基于进化结构优化算法,通过定义单元应力指标函数,结合结构轻量化目标设计,确定优化模型的目标函数;结合变密度SIMP材料理论模型,定义单元权重函数为优化函数的自变量参数,并根据单元平均应力给出单元权重函数的递推迭代关系式;结合有限元平衡方程以及应力指标上限建立单元生长进化拓扑优化算法的数学模型。通过对其解析计算分析,指出优化目标函数最小即要求拓扑构型体积函数最小;最后结合迭代终止条件给出具体的考虑应力指标的单元生长拓扑优化流程。
通过对VLCC中剖面横撑结构的优化计算,对比了单元生长进化算法和基于ANSYS平台的连续体拓扑优化准则算法,从优化结果对比中看出,单元生长进化算法能得到更加简单清晰的拓扑构型。本文最后根据优化的拓扑构型给出了一种取消VLCC中剖面横撑结构的设计方案。
[1]刘远东,尹益辉,胡文军,等.圆形阻尼层合板的拓扑优化设计及其实验验证[J].振动与冲击,2012(22):76-79. Liu Yuandong,Yin Yihui,et al.Topologic Optimal design of a circular laminated damping plate with its experimental verification[J].Journal of Vibration and Shock,2012(22):76-79.
[2]王仁华,赵宪忠,等.平面桁架结构拓扑优化设计的改进智能算法[J].工程力学,2012(11):205-211. Wang Renhua,Zhao Xianzhong,et al.Improved intelligent algorithm for topology optimization design of planar truss structure[J].Engineering Mechanics,2012(11):205-211.
[3]Chan C M,Zhang L M,Ng J T M.Optimization of pile groups using hybrid genetic algorithms[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(4):497-505.
[4]Kaveh A,Talatahari S.Particle swarm optimizer,ant-colony strategy and harmony search scheme hybridized for optimization of truss structures[J].Computers&Structures,2009,87(5/6):267-283.
[5]Kaveh A,Talatahari S.Optimum design of skeletal structures using imperialist competitive algorithm[J].Computers& Structures,2010,88(21/22):1220-1229.
[6]Gomes H M.Truss optimization with dynamic constraints using a particle swarm algorithm[J].Expert Systems with Applications,2011,38(1):957-968.
[7]何林伟,蔡国平.连续结构拓扑优化的一种简单实现[J].机械强度,2012,34(5):687-691. Hen Linwei,Cai Guoping.Simple approach to structural topology optimization for continuous structures[J].Journal of Mechanical Strength,2012,34(5):687-691.
[8]Amstutz S,Novotny A A.Topological optimization of structures subject to von Mises stress constraints[J].Structural and Multidisciplinary Optimization,2010,41:407-420.
[9]张宇,罗陆峰.基于SIMP插值模型的棋盘格现象滤波控制算法研究[J].制造业自动化,2012(10):81-84. Zhang yu,Luo Lufeng.Research on filter control algorithm for the checkerboard phenomenon based on SIMP interpolation model[J].Journal of Manufacture and Automation,2012(10):81-84.
[10]Lotfi K G,Sherif A M,Ashraf O N.A particle swarm-based genetic algorithm for schedul-ing in an agile environment[J]. Computers&Industrial Engineering,2008,55(3):707.
[11]胡兴国,程赫明,位向飞.根据排序移除低效材料的渐进结构优化方法研究[J].科学技术与工程,2012(10):7261-7265. Hu Xingguo,Cheng Heming,Wei Xiangfei.Evolutionary structural optimization by removing inefficient material according to the rank of material’s efficiency[J].Science Technology and Engineering,2012(10):7261-7265.
[12]Rong J H,Xie Y M,Yang X Y.An improved method for evolutionary structural optimization against buckling[J].Computers and Structures,2001,79(3):253-263.
[13]王雷.连续结构体的SKO优化方法研究[J].设计与分析,2012(27):135-137. Wanglei.The SKO optimization algorithm applying on the continuous structure[J].Design and Analysis,2012(27):135-137.
[14]左中杰,干泉,王运兴,等.基于渐进结构优化法的拱坝结构曲线函数优化[J].土木工程与管理学报,2012(6):93-98. Zuo Zhongjie,Gan chuan,et al.Optimization research of Arch Dam structure curve function based on the evolutionary structural optimization algorithm[J].Joural of Civil Engineering and Management,2012(6):93-98.
[15]Huang X,Xie Y M.Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J].Computational Mechanics,2009,43(3):393-401.
[16]Xie Y M,Steven G P.Shape and layout optimisation via an evolutionary procedure[C].In:Proceedings of International Conference on Computational Engineering Science.Hong Kong University of Science and Technology,1992:17-22.
Applying the evolution topology algorithm to the VLCC’s mid-section structure optimization
LIU Hong-liang1,XIA Li-jüan1,WU Jia-meng2
(1.State Key Laboratory of Ocean Engineering,Shanghai Jiaotong University,Shanghai 200240,China; 2.Marine Design and Research Institute of China,Shanghai 200011,China)
Evolutionary structural topology optimization shows some specific features compared with other topology optimization algorithms.Which can be applied on the optimization design of the VLCC mid-section cross-brace structure.According to the element’s stress index and the element weight coefficient,the objective function was established.Then,the iteration equation of the element’s weight coefficient was created based on the obtained element stress.Finally,combining the FEM’s balance equation the total optimization mathematical model was created.The mathematical calculation results show that the objective function depends mainly on the model’s volume function.Compared with the result of the ANSYS continuous structure topology optimization,the calculation with the evolution algorithm is more simple and efficient. This method using in this paper may provide something useful to the VLCC’s lightweight design.
evolutionary structural optimization;topology optimization;stress index; VLCC mid-section optimization;VLCC(very large crude oil carrier)
U662
A
10.3969/j.issn.1007-7294.2017.04.011
1007-7294(2017)04-0464-08
2016-10-21
国家自然科学基金资助项目(50909060);海洋工程国家重点实验室青年创新基金资助(GKZD010059-20)
刘宏亮(1989-),男,硕士研究生,E-mail:76908358liang@sjtu.edu.cn;夏利娟(1975-),女,副教授。
——工程地质勘察中,一种做交叉剖面的新方法

