流激孔腔噪声特征及控制方法研究
刘璐璐,吕世金,刘进
(中国船舶科学研究中心船舶振动噪声重点实验室,江苏无锡214082)
流激孔腔噪声特征及控制方法研究
刘璐璐,吕世金,刘进
(中国船舶科学研究中心船舶振动噪声重点实验室,江苏无锡214082)
文章利用大涡模拟方法,建立了流激孔腔自噪声及辐射噪声预报方法,分析了腔深、来流速度及孔腔流向尺寸对剪切振荡特征的影响,并给出了流激孔腔近场辐射噪声特性。在此基础上探索了流激孔腔噪声控制方法,研究了孔腔开口加格栅对流激孔腔涡流场和噪声特征的影响。
大涡模拟;流激孔腔;剪切振荡;格栅
0 引言
水下航行体由于潜浮的需要,开设了数量众多、样式各异的流水孔和压载水舱开口以及其它大小切口。水下航行水流经过开口表面时,由于表面的不连续性,流动发生分离,沿流向跨越孔腔的内、外流之间,存在不稳定的剪切层波动,一方面直接辐射噪声,另一方面会在流水孔后缘局部区域造成湍流边界层脉动压力增大,激励航行体轻外壳振动从而产生二次辐射噪声。此外,对于采用双层壳体的航行体,开口在轻外壳与耐压壳之间形成孔腔,声波在有限孔腔中传播会形成驻波,其驻波共振频率与孔腔尺寸有关,如果开孔的剪切振荡频率与孔腔驻波共振频率相一致,即形成耦合,会产生强烈的声辐射。这种声辐射表现为若干个以耦合共振频率为中心频率的窄带噪声[1]。因而研究孔腔流动与发声机理并探索流激孔腔噪声控制方案具有重要意义。早期的研究基于试验测试为主,随着数值模拟方法尤其是大涡模拟方法的出现和发展,使得从数值模拟角度研究孔腔流激噪声成为可能。
近年来,国内外研究者针对流激孔腔噪声控制方式进行了大量的探索。被动流动控制技术由于结构简单、应用方便成为最早被研究的流动控制方法。Kuo[2]采用激光多普勒测速仪及激光切片技术,在水筒中测量了倾斜腔底对空腔剪切层脉动特征的影响。结果表明,低Re数情况下,在一定倾斜范围内,倾斜腔底对空腔剪切层振荡产生调制作用,可明显降低腔内振荡幅度,倾斜达到一定程度,自激振荡完全抑制。Zhang和Rona[3]设计了一种在空腔前缘放置的斜坡块,对空腔噪声具有一定的抑制效果。但这种方法与来流的马赫数有很大关联,因此不同高度、角度的斜坡块只能对特定流速的流体有控制效果。Tzborda[4]在空腔内部添加不同高度的栅栏并进行了大量的风洞试验,试验结果表明这种控制方法能够有效降低腔内前后部的压力差。Arunajatesan[5]采用数值模拟方法,计算分析了格栅肋条对剪切层振荡的影响。结果表明孔腔开口加肋条后,开口仍然有剪切层振荡现象出现,清晰可见类似于共振腔的大尺度旋涡,但是,格栅肋条对腔颈部位的流场有明显的调制作用。朱习剑和何祚镛[6]在水筒中进行了变深度的、不带导流板的突出矩形腔的振荡和声辐射研究。吴亚军[7]在孔腔上游安装了圆柱形、矩形、锯齿和三角形四种形式的扰流体,控制孔腔的流激振荡,对窄带或宽带噪声有一定的抑制效果。
本文利用大涡模拟方法,建立流激孔腔自噪声及辐射噪声预报方法,数值分析孔腔开口噪声特征,考察腔深、来流速度、流向尺度等参数对流激孔腔剪切振荡的影响以及流激孔腔近场辐射噪声特征,并探索孔腔开口加格栅结构对流激孔腔涡流场和噪声特征的影响规律。
1 流激孔腔噪声计算方法
1.1 计算方法
1.1.1 大涡模拟方法
流激孔腔流动特征通过不可压缩流动方程求解。大涡模拟的理论建立在两个基本假设之上:第一个是湍流的平均特性,主要由大尺度湍流运动来控制,几乎不受小尺度湍流运动的影响。第二个假设是小尺度湍流,特别在高雷诺数下,表现出各向同性的特点。通过将非定常的N-S方程在波数空间或物理空间上进行滤波,得到大涡模拟的控制方程。滤波过程有效的过滤掉了那些尺度小于滤波宽度(或网格尺度)的小涡。
滤波变量由下式定义:

其中:D为流体域,G为决定可求解涡尺度的滤波函数。可选用不同的滤波函数,本文采用网格体积滤波。
滤波后的连续性方程和N-S方程可以表示为:
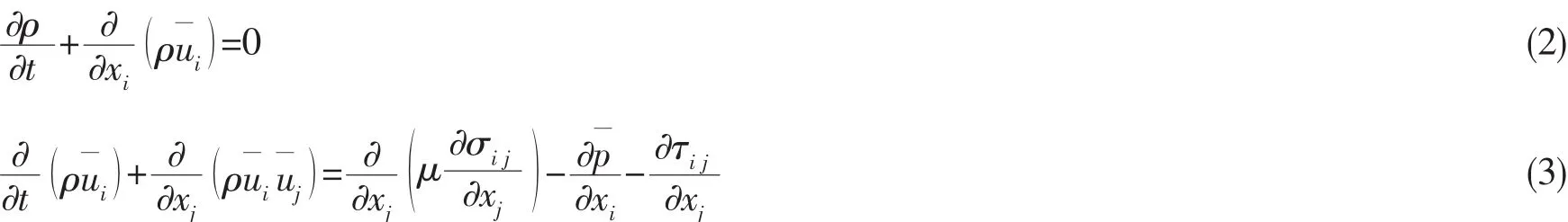
其中:σij为分子粘性引起的应力张量,τij为亚格子应力,需用亚格子涡模型进行模拟:

Smagorinsky模型由Smagorinsky[8]于1963年提出。该模型基于小尺度涡是局部平衡状态的假设,因此可用涡粘形式的亚格子雷诺应力模型表示:

其中:Cs为Smagorinsky常数,动态Smagorinsky模型采用多重网格滤波的方法将参数Cs与计算过程的湍流物理量的变化相关联,通过大涡模拟本身的计算结果,可以在每个空间网格点、每个时间步计算模型参数Cs,完全摆脱了一般理论中的经验参数。此时Cs是随湍流物理量的时间和空间变化的函数。
1.1.2 声学类比方程
流体的扰动产生声场,声场模拟采用声学类比方法。声学类比方法就是对流动和噪声分别处理,将声波的产生与传播进行解耦,即从流动的数值模拟中计算出声源项,忽略声波的传播与反馈对声源的干扰,然后通过波动方程的解析解亦即格林积分公式来预报远场噪声。
Ffowcs Williams与Hawkings声学类比方程,即FW-H方程[9]表达如下:
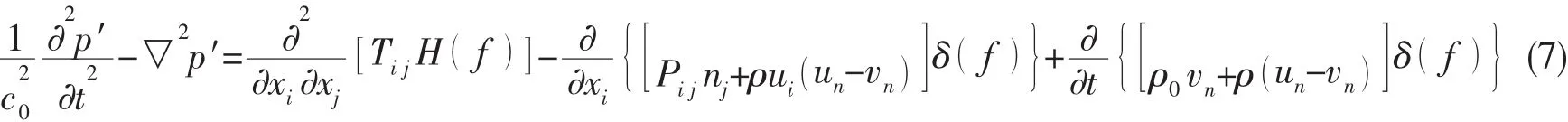
其中:ui为xi方向的流体速度分量;un为垂直于物体表面(f=0)的流体速度分量;vi为xi方向的物体表面速度分量;vn为物体表面法向速度分量;δ(f)为Dirac delta函数;H(f)为Heaviside阶跃函数。p′为远场声压。f=0表示物体表面,f>0表示外部无界的自由空间。ni为物面外法线,指向流体内部。c0为远场声速,ρ0为远场密度,Tij为Lighthill应力张量。

利用自由空间格林函数δ(g)/4πr,结合Kirchhoff积分可求出FW-H方程的远场解。远场噪声中包含单极子噪声pT′(x,t),偶极子噪声pL′(x,t)以及四极子噪声pQ′(x,t)。

1.2 计算模型
本文在大涡模拟和声学类比方法的理论框架下,结合动态Smagorinsky亚格子应力模型,计算了三维孔腔的流激噪声,并与试验结果进行了比较,验证了流激噪声预报方法的可行性。在此基础上探究了流激孔腔噪声控制方案,并评价了噪声控制效果。
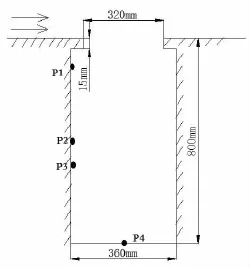
图1 开口空腔结构示意图Fig.1 Schematic of flow-induced cavity
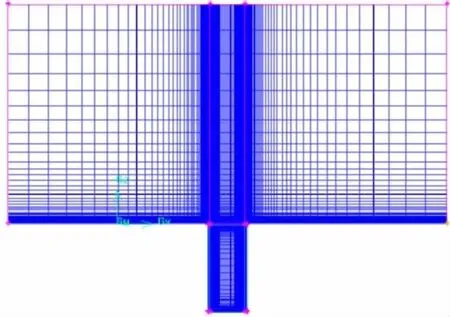
图2 计算模型网格划分图Fig.2 The computational domain and grid
研究的流激孔腔开口长320 mm,宽194 mm,深15 mm,开口下方矩形腔体深度785 mm,长360 mm,宽215 mm,自噪声监测点如图1。数值模拟计算域长和宽均为4 m,高2 m,进口采用自由来流条件,来流速度为6 m/s,出口为压力出口,其它均为无滑移壁面。网格划分图如图2所示。亚格子应力模型采用Dynamic Smagorinsk-Lilly模型,动量方程的离散采用有限体积法,压力速度耦合算法采用SIMPLE算法,时间项的离散采用二阶隐式差分格式,而空间项的离散采用二阶精度的限界中心差分格式。计算时间步长为0.000 2 s,分析频率为2 500 Hz。
1.3 计算方法验证
为了验证计算模型的可靠性,设计开口尺寸可变孔腔模型,可实现0~320 mm范围任意选取。流激孔腔噪声测试在中国船舶科学研究中心小型高速空泡水筒进行。自噪声测试利用方形水洞225 mm× 225 mm×845 mm长试验段,开口腔体换掉原有机玻璃观察窗,开口宽度设计为194 mm,长320 mm,开口下方腔体总深度800 mm,长度360 mm,宽度215 mm,如图3所示,在腔体内与数值模拟监测点相同位置处布置4个水听器,研究开口附近及腔体内不同位置的噪声特征。

图3 开口腔体实图Fig.3 Experimental set-up of cavity noise measurement
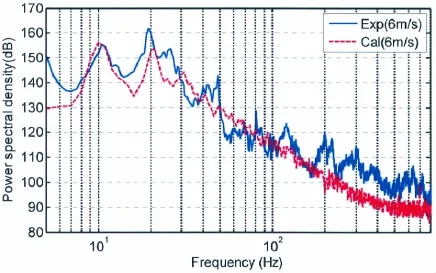
图4 流激孔腔噪声窄带频谱预报与试验结果比较Fig.4 Comparison of computed and experimental frequency spectra for flow-induced cavity
Rossiter[10]给出了辨识流动模态振荡频率的经验公式为
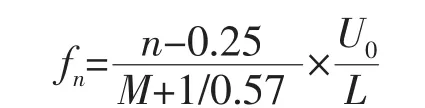
其中:fn为模态振荡频率、n为模态数、U0为远方来流速度、M为马赫数、L为孔腔开口长度。
图4给出了水速为6 m/s时同一监测点处(P1)320 mm开口流激孔腔自噪声计算与试验结果比较。表1给出了本文针对开口长度为320 mm的孔腔剪切振荡频率的试验、计算和理论结果比较,可以看出计算和试验结果剪切振荡频率基本一致,总声级偏差小于4 dB。这表明本文计算结果可信,可用来分析流激孔腔剪切振荡特征。
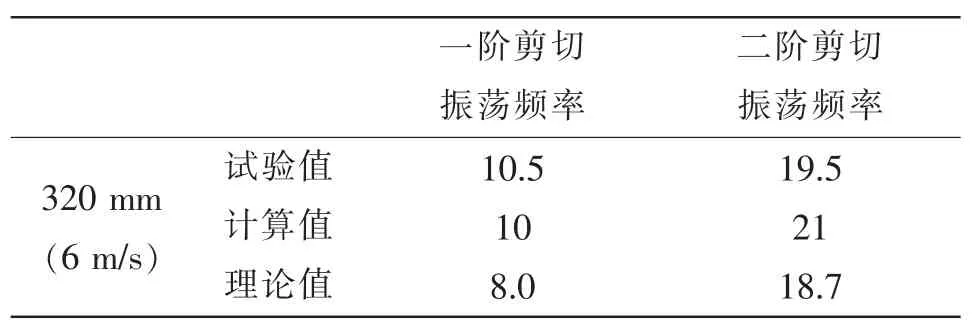
表1 剪切振荡频率的计算值与试验、理论值比较Tab.1 Comparison of computed,experimental and theoretical shear oscillation frequency
2 流激孔腔噪声特征分析
流激孔腔开口处流体的剪切振荡产生孔腔线谱噪声,因此考察孔腔流场特性是噪声特征分析的第一步。流激孔腔中纵面展向涡量场如图5所示。非定常绕流剪切层从孔腔开口上游角区开始分离并发展,剪切层中的涡发生对流传递,到达随边附近时击打随边,使随边产生压力脉冲。压力脉冲以声速向上游传播反馈到导边。满足一定相位条件时,剪切层扰动形成闭合反馈环,产生自持振荡[1]。振荡的流体作为一种等效声源,在一定条件下有可能产生单调音或者宽带噪声。
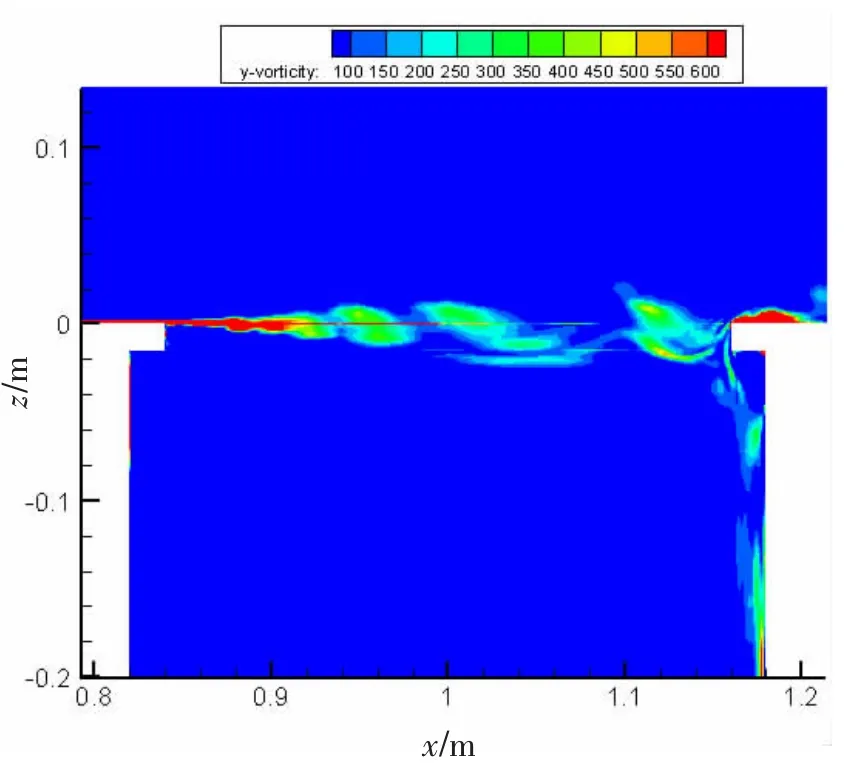
图5 320 mm开口涡量场Fig.5 Vorticity field of 320 mm cavity
2.1 流激孔腔自噪声特征分析
为了分析腔深对孔腔自噪声功率谱的影响,分别选取腔深为400 mm、800 mm及1 200 mm。针对开口长度为50 mm的孔腔,来流速度为6 m/s时不同腔深自功率谱计算结果比较如图6所示。腔深从400mm增加至800 mm,剪切振荡频率不变,一阶剪切振荡频率峰值降低。若继续增加腔深到1 200 mm,剪切振荡频率和峰值不再变化,自功率谱曲线重合。表明腔深大于800 mm时,流激孔腔自功率谱不再受腔深影响。故下文计算均取腔深800 mm。
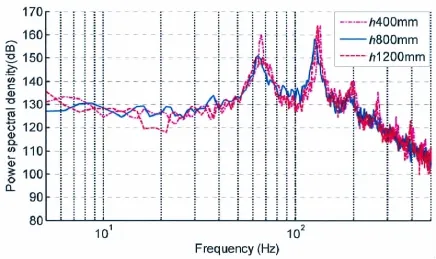
图6 不同腔深对孔腔自功率谱的影响Fig.6 Influence of cavity depth on flow-induced cavity noise
来流速度对流激孔腔自噪声的影响如图7,分别考察了4.5 m/s、6 m/s和9 m/s来流速度下,320 mm开口孔腔的自噪声(P1)频谱曲线。随着流速增加,流激孔腔剪切振荡峰值频率向高频移动。来流速度从4.5 m/s增至9 m/s,对应一阶剪切振荡频率从8 Hz增加到16 Hz,二阶剪切振荡频率从16 Hz向高频偏移至32 Hz。此外,5~500 Hz频段总声级分别为166 dB、170 dB和175 dB,流速每增加一倍,总声级增加约9 dB。
为了分析开口流向尺寸对流激孔腔噪声的影响,计算了20 mm、50 mm、100 mm、150 mm、200 mm和320 mm等几种开口附近自噪声。图8为6 m/s时不同流向尺寸开口附近(P1)自功率谱级比较曲线。随着开口尺寸增加,流激孔腔自噪声线谱峰值频率向低频偏移。开口尺寸从20 mm增加至320 mm,对应的一阶剪切振荡频率从140 Hz向低频偏移至11 Hz,二阶剪切振荡频率从281 Hz减小至21 Hz。由此可见开口流向尺寸越高,孔腔剪切振荡频率越低。
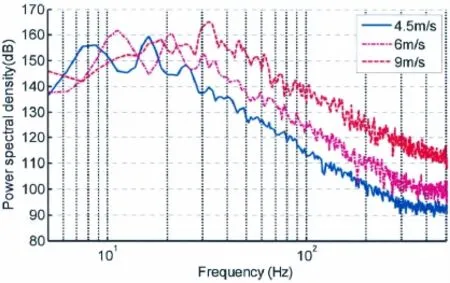
图7 来流速度对流激孔腔自噪声的影响Fig.7 Influence of inflow velocity on flow-induced cavity noise

图8 6 m/s时不同开口尺寸对孔腔附近自噪声的影响Fig.8 Influence of streamwise length on flow-induced cavity noise
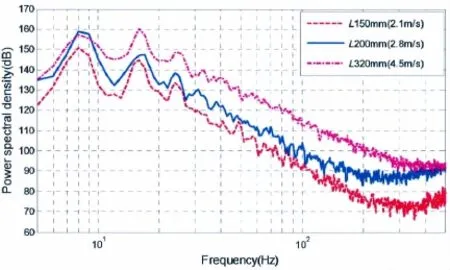
图9 U0/L为定值时流激孔腔自功率谱计算结果Fig.9 Comparison of auto-spectrum for flow-induced cavity when U0/L=constant
图9给出了U0/L为定值情况下三个不同开口尺寸(150 mm、200 mm和320 mm)、对应不同流速(2.1 m/s、2.8 m/s和4.5 m/s)的孔腔自功率谱曲线计算结果。可以看出剪切振荡峰值频率重合,由此可以推断流激孔腔剪切振荡频率与U0/L成比例。该结论也与Rossiter[10]提出的流动模态振荡频率经验公式相吻合。在剪切振荡峰值频率一致的情况下,随着流速增加,剪切振荡峰值增加,自功率谱总声级也不断增加。
2.2 流激孔腔近场辐射噪声特征分析
对流激孔腔的近场辐射噪声计算监测点如图10所示,在孔腔开口中心正上方流向-法向平面R=1.7 m和R=1 m处分别布置五个声压接收器,考察6 m/s时流激孔腔辐射噪声变化规律。
图11-12分别给出了流向-法向平面距50 mm孔腔开口中心不同距离、不同方向处的近场辐射噪声。可以看出,f<100 Hz时流激孔腔辐射噪声在不同方向上计算结果有显著差异,表明流激孔腔辐射噪声具有指向性,且主要集中在低频区域。此外,近场辐射噪声线谱峰值频率与流激孔腔自噪声一致,且线谱峰值强度较低,没有出现强烈的振荡,可以推断腔口剪切振荡和空腔声模态没有耦合共振。事实上本文数值模拟过程假定腔体壁面是刚性,此时由于声波波长较长,水介质空腔中的声模态频率远高于腔口流体动力振荡频率,腔口剪切振荡与腔体声模态产生耦合的可能性很小,一般不会出现较强的低频线谱噪声。而实际腔体壁面是弹性的,弹性壁面提供的附加柔度会降低腔体的声模态频率,使得腔口剪切振荡频率与空腔的模态频率耦合的可能性增大。
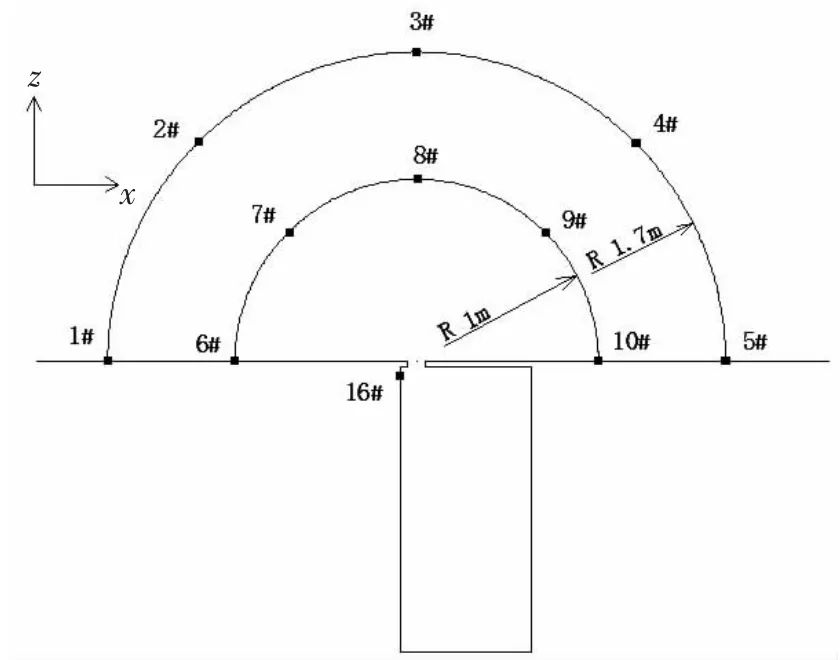
图10 辐射噪声计算监测点(流向—法向平面)Fig.10 Monitoring points for radiated noise calculation (streamwise-wall-normal plane)
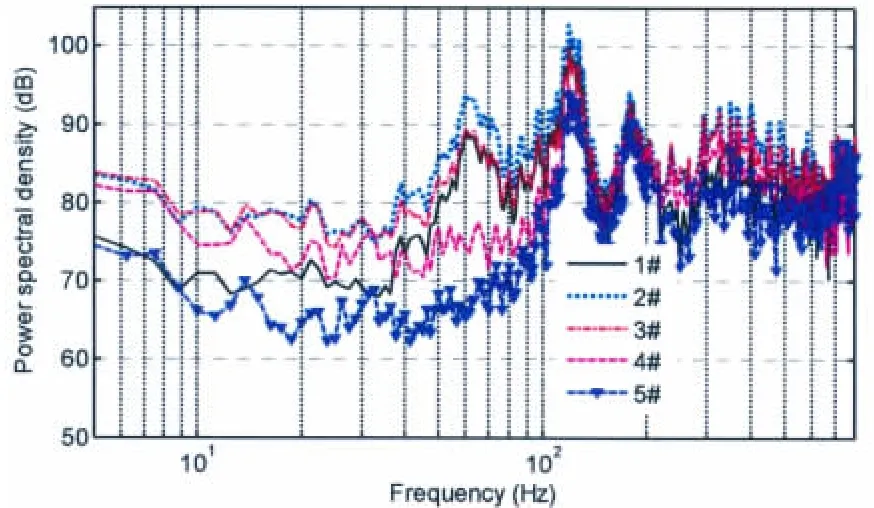
图11 距50 mm孔腔开口中心R=1.7 m处中纵面不同方向测点的辐射噪声Fig.11 Radiated noise of different directions in streamwise-wall-normal plane at R=1.7 m for 50 mm long cavity

图12 距50 mm孔腔开口中心R=1 m处中纵面不同方向测点的辐射噪声Fig.12 Radiated noise of different directions in streamwise-wall-normal plane at R=1 m for 50 mm long cavity
3 格栅对流激孔腔噪声特征的影响
常用的流激孔腔剪切振荡及声辐射控制方式主要包括在腔口导边布放扰流器及流动扩散器,或在随边布放流动偏转器。对流激孔腔进行格栅处理可以改变孔腔流体的流动特性和相位关系,并进一步导致孔腔的声场特性发生变化。本文探索了开口加格栅对流激孔腔剪切振荡及声辐射的控制效果。
3.1 格栅形式及参数
本文对320 mm开口孔腔进行加格栅处理,分直立格栅和斜立格栅两种方案,格栅间距均为50 mm。开口加直立格栅和斜格栅示意图分别如图13、图14所示,模拟水速6 m/s时直立格栅和斜格栅对流激孔腔线谱噪声的影响。
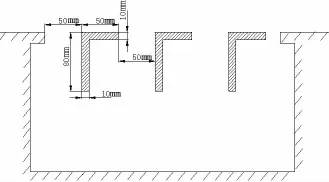
图13 320 mm开口加直立格栅示意图Fig.13 Schematic of 320 mm long cavity with upright grille
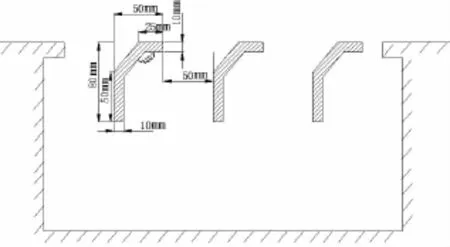
图14 320 mm开口加斜格栅示意图Fig.14 Schematic of 320 mm long cavity with oblique grille
3.2 格栅对流激孔腔涡流场的影响
要考察格栅对流激孔腔噪声特征的影响,首先需要清楚格栅结构对孔腔流场特性的调制作用。320 mm大开口孔腔加直立格栅和斜立格栅后的展向涡量场分别如图15~16。格栅的存在使孔腔开口附近的大尺度涡分解为小尺度涡,且孔腔加斜格栅结构时剪切层中的涡在下游壁面处破碎。如前文所述,流激孔腔剪切振荡的成因在于孔腔内部剪切层的不稳定性,且这种不稳定性会由于下游壁面的反馈机制被增强,下游角区的干扰以回馈环的形式反作用于上游角区边界层分离点。斜立格栅相比于直立格栅角区平缓过渡,剪切层中的涡发生对流传递到达随边并击打倾斜的下游壁面,壁面产生的压力脉冲较小,下游壁面的反馈机制较弱,因而流激孔腔剪切振荡强度较小。由此可以断定,斜立格栅对流激孔腔涡流场的调制作用效果优于直立格栅。
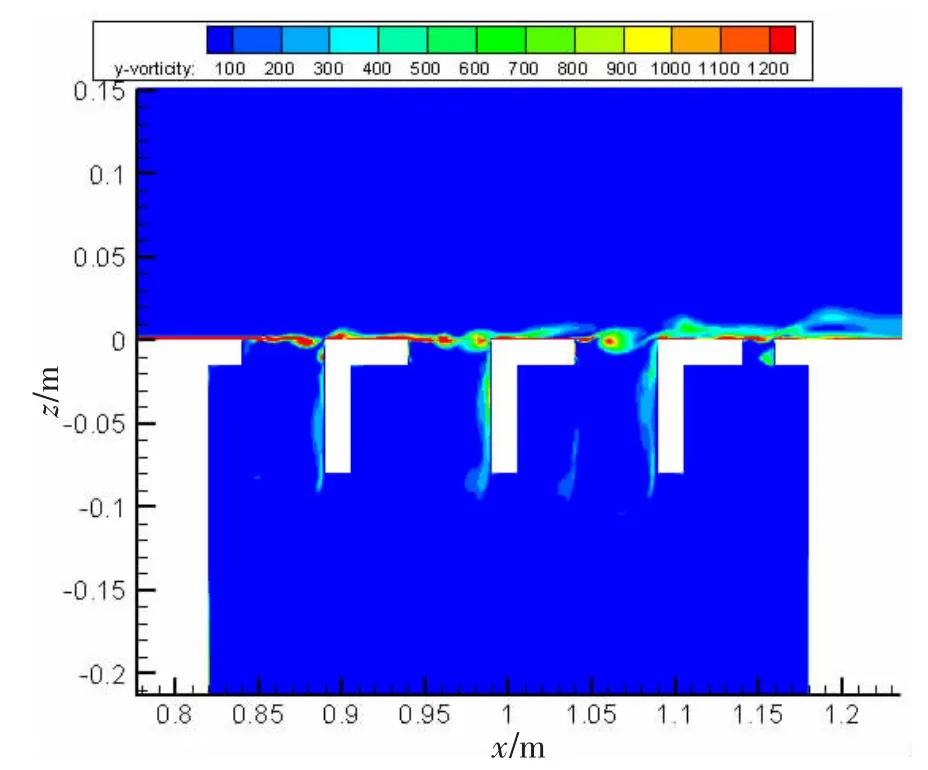
图15 320 mm开口加直立格栅对应的涡量场Fig.15 Vorticity field of 320 mm cavity with upright grille
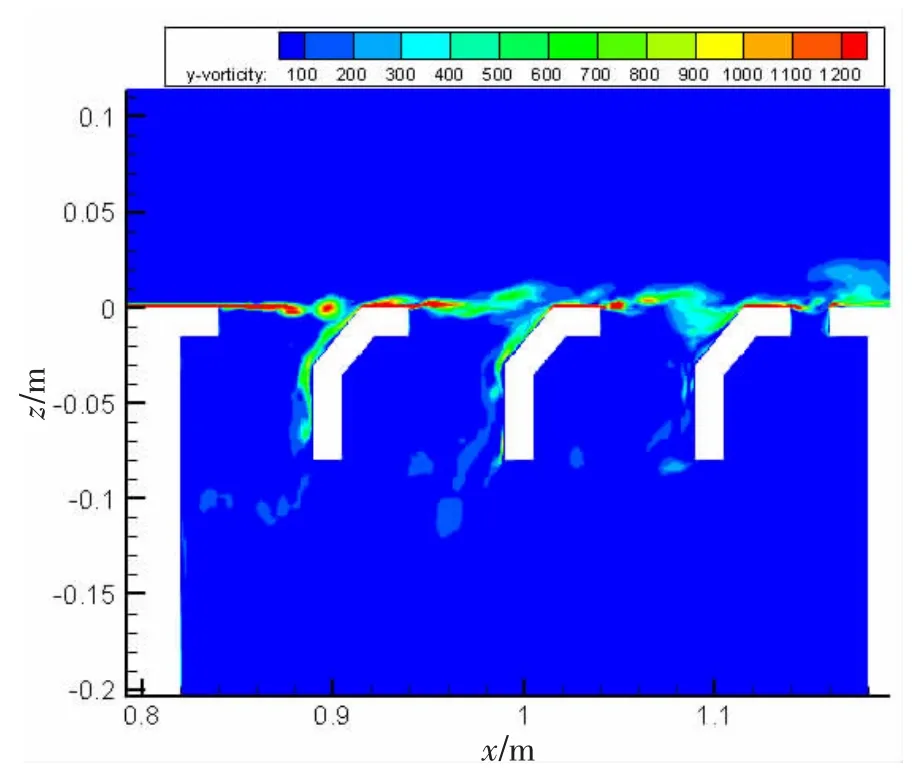
图16 320 mm开口加斜立格栅对应的涡量场Fig.16 Vorticity field of 320 mm cavity with oblique grille
3.3 格栅对流激孔腔噪声特征的影响
图17给出了两种格栅对320 mm开口孔腔结构自功率谱的影响,320mm开口流激孔腔及加直立格栅和斜立格栅时自功率谱在5~500 Hz频段总声级分别为170 dB、161 dB和152 dB。孔腔加格栅使得在f<50 Hz频段范围内自噪声功率谱曲线大幅下降。此外,加直立格栅后剪切振荡峰值频率向高频偏移,一阶峰值频率从11 Hz向高频偏移至66 Hz,二阶峰值频率从21 Hz增大至124 Hz,且峰值相比于未加格栅情况显著下降。加斜立格栅情况下开口孔腔自功率谱曲线较平缓,没有峰值出现,斜立格栅对开口孔腔自噪声的调制效果较好,这与前文对涡流场的分析结果相吻合。
对320 mm大开口孔腔加均匀等间距格栅时自噪声频谱曲线与50 mm开口孔腔的比较如图18所示。320 mm大开口孔腔加直立格栅对应的自噪声频谱与50 mm开口孔腔几乎一致,峰值频率一一对应,但峰值略有降低,而加斜格栅时自噪声频谱曲线峰值消失。说明对于水下航行体上的大开口,格栅相当于将大开口变为等格栅间距的多个小开口。因此在开口尺寸不可调的前提下,可通过加直立格栅或者斜格栅控制流激噪声。
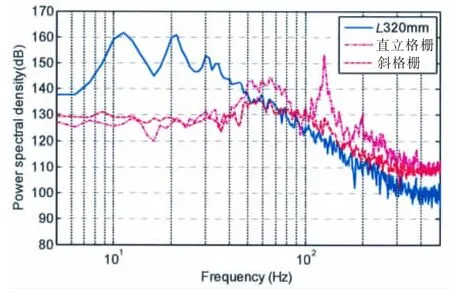
图17 两种格栅对320 mm开口自功率谱的影响Fig.17 Influence of grille on auto-power spectra of 320 mm long cavity
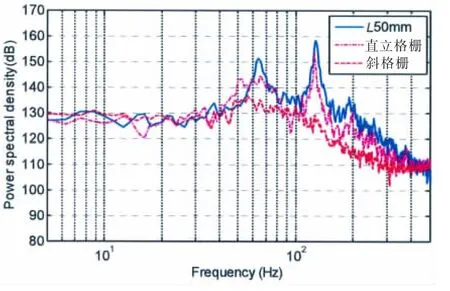
图18 两种格栅与50 mm开口自功率谱比较Fig.18 Comparison of auto-power spectra between grilled 320 mm long cavity and 50 mm long cavity
进一步考察两种格栅对320 mm开口孔腔结构近场辐射噪声的影响,如图19所示。从图中可以看出两种格栅对流激孔腔辐射噪声的控制效果无显著差异,计算可知流激孔腔加格栅使近场辐射噪声总声级在5~500 Hz频段下降约14 dB。
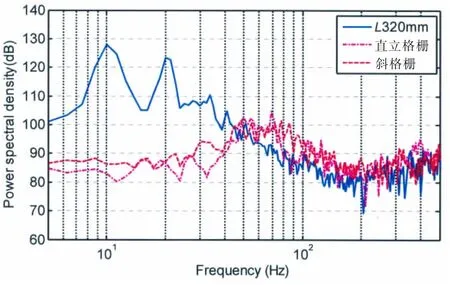
图19 两种格栅对320 mm开口辐射噪声的影响Fig.19 Influence of grille on radiated noise power spectra of 320 mm long cavity
4 结论
本文利用大涡模拟数值方法,建立了流激孔腔自噪声及辐射噪声预报方法,并与试验结果吻合较好;分析腔深、来流速度和流向尺寸对流激孔腔自噪声功率谱的影响以及近场辐射噪声特性;研究了孔腔开口加不同格栅形式对孔腔涡流场和噪声特征的影响,得到以下主要结论:
(1)流激孔腔剪切振荡频率与U0/L成比例。近场辐射噪声线谱峰值频率与流激孔腔自噪声一致,且线谱峰值强度较低,没有出现较强的低频线谱噪声。
(2)对大开口加直立格栅使剪切振荡频率向格栅间距开口剪切振荡频率偏移,且峰值下降;斜格栅对孔腔开口流场的调制作用效果较好,噪声控制效果优于直格栅,使流激孔腔自功率谱曲线较平缓,剪切振荡峰值消失。流激孔腔加格栅使近场辐射噪声总声级在5~500 Hz频段下降约14 dB。
本文对流激孔腔噪声特征的数值模拟在假定腔体为刚性壁的前提下腔口剪切振荡和腔体声模态没有耦合共振。未来进一步的研究方向是重视腔壁弹性振动与空腔声共振和腔口剪切层振荡之间的耦合作用,尝试将腔壁弹性纳入数值模拟过程,探索腔口剪切振荡与腔体声驻波的耦合共振,并通过调整水下空腔弹性壁参数来抑制腔口剪切振荡与空腔声模态水弹性耦合共振,多层面控制水下流激孔腔的线谱噪声。
[1]俞孟萨,张铮铮,高岩.开口与空腔流激声共振及声辐射研究综述[J].船舶力学,2015,19(11):1422-1430. Yü Mengsa,Zhang Zhengzheng,Gao Yan.A review of acoustic resonant and radiation of aperture and cavity by flow excitation[J].Journal of Ship Mechanics,2015,19(11):1422-1430.
[2]Kuo C H,Huang S H.Influence of flow path modification on oscillation of cavity sheer layer[J].Experiments in Fluids, 2001,31:162-178.
[3]Zhang X,Rona A,Edwards J A.An observation of pressure waves around a shallow cavity[J].Journal of Sound and Vibration,1998,214(4):771-778.
[4]Taborda N,Bray D,Knowles K.Passive control of cavity resonances in tandem configurations[C].Proc 31st AIAA Fluid Dynamics Conference,2001.
[5]Arumajatesan S,Sinha N.Modeling approach for reducing Helmholtz resonance in submarine structures[R].AO-A458237, 2005.
[6]朱习剑,何祚镛.水洞中突出矩形腔的流激驻波振荡研究[J].哈尔滨船舶工程学院学报,1993,14(4),41-52. Zhu Xijian,He Zuoyong.Study of flow-induced standing wave resonance of rectangular cavity in water tunnel[J].J of Harbin Shipbuilding Engineering Institute,1993,14(4):41-52.
[7]吴亚军,等.基于被动控制的空腔脉动实验研究[J].工程热物理学报,2013,34(9):1640-1644.Wu Yajun,Ouyang Hua,Huang You.Experimental investigation on the fluctuating pressure of cavity based on passive controls[J].J of Engineering Thermo Physics,2013,34(9):1640-1644.
[8]Smagorinsky J.General circulation experiments with the primitive equations.I.The basic experiment[J].Month.Wea.Rev., 1963,91:91.
[9]Ffowcs Williams J E,Hawkings D L.Sound generation by turbulence and surfaces in arbitrary motion[C]//Proc.Roy.Soc.. London,264 A,1969:321-342.
[10]Rossiter J E.Wind tunnel experiments on the flow over rectangular cavities at subsonicand transonic speeds[J].Rep.Mem. 3438,Aeronautical Research Council,1964.
[11]Crighton D G,Dowling A P,Ffowcs Williams J E,Heckl M,Leppington F G.Modern methods in analytical acoustics[M]. Springer-Verlag London Limited,1992.
[12]张楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.
[13]刘进,吕世金,沈琪.流激开孔空腔噪声数值预报方法研究[C].水下噪声会议论文集,2015.
Characteristics and control of cavity noise induced by flow excitation
LIU Lu-lu,LÜ Shi-jin,LIU Jin
(National Key Laboratory on Ship Vibration&Noise,China Ship Scientific Research Center,Wuxi 214082,China)
Using large eddy simulation method,a prediction method for flow induced cavity noise was established.The inlet velocity,cavity depth and streamwise length influence on shear oscillation characteristics were analyzed,and nearfield radiate noise characteristics were given.A research on noise control scheme was performed and the influence of grille on flow induced cavity noise characteristics was studied.
large eddy simulation;flow-induced cavity;shear oscillation;grille
O352
A
10.3969/j.issn.1007-7294.2017.04.014
1007-7294(2017)04-0493-10
2017-01-22
刘璐璐(1990-),女,工程师,E-mail:LL300100@aliyun.com;吕世金(1973-),男,研究员。

