基于量子行为遗传算法的船体局部结构优化设计

刘波，林焰，吕振望，管官，纪卓尚

（大连理工大学a.工业装备结构分析国家重点实验室；b.船舶工程学院，辽宁大连116024）

基于量子行为遗传算法的船体局部结构优化设计

刘波a，林焰a，吕振望b，管官b，纪卓尚b

（大连理工大学a.工业装备结构分析国家重点实验室；b.船舶工程学院，辽宁大连116024）

采用遗传算法解决船舶复杂结构中混合设计变量优化问题时，其效果很有效，且能获得全局最优可行解。然而，简单遗传算法局部搜索能力差且易于早熟。为了提高对船舶复杂结构设计变量解空间的搜索能力，该文设计了一种基于二进制编码的适用于混合变量的量子行为遗传算法，比较适合于复杂函数的全局寻优，且搜索能力优于标准遗传算法。通过三个算例对算法的寻优能力进行测试，实验结果表明，采用量子行为遗传算法进行的船体局部结构优化设计具有较好的计算质量与计算效率。

量子行为遗传算法；船体局部结构；结构优化设计；混合设计变量；搜索能力

0 引言

在船舶结构设计中，为了在满足设计条件（如强度、刚度、材料选择及制造工艺要求等）下设计出合理的结构形式和尺寸，人们最初是借助于数学最优化方法来实现结构的最优化设计。后来随着计算机技术的发展，船舶结构优化设计新方法亦不断涌现，如以模糊数学为基础的模糊优化设计方法[1-2]、以人工智能为基础的专家系统法[3]与神经网络方法[4]、以仿生学为基础的进化算法（遗传算法[5-7]，蚁群算法[8]，粒子群算法[9]，人工蜂群[10]）等在船舶结构优化设计中得到了广泛的应用。近年来，特别是仿生优化算法更是人们追逐的热点问题，与传统的数学最优化方法相比较，它具有使用简便、不依赖于求解问题的数学特征以及全局寻优能力强等优点。但是，当面对规模较大的复杂系统优化设计问题时[11-12]，标准的进化算法往往会出现早熟现象，因而很难搜索到全局最优解，甚至得不到工程可靠解。为了解决这一困难，在应用标准进化算法进行结构优化设计时大都需要改进，本文针对标准遗传算法在船舶结构优化设计过程中出现的迭代时间长、收敛速度慢和易于陷入局部极值等现象，采用了量子算法和遗传算法的融合算法—量子行为遗传算法[13]进行船体局部结构优化设计，目前该方法主要用于解决0-1背包问题和多目标优化问题，但在船舶设计领域还鲜有报道。

量子行为遗传算法是由Narayanan和Moore等人于1996年最先提出来的一种新型概率进化算法，该算法将量子多宇宙的概念引入到遗传算法中用于求解TSP问题。与标准遗传算法相比其搜索效率更高，但算法原理仍属于遗传算法范畴。后来，Han等人又将种群的迁移机制和量子的态矢量等概念引入进遗传算法中，提出了另外一种量子行为遗传算法的计算模型[14-15]，该种算法比标准遗传算法具有更好的种群多样性及较高的搜索能力。目前国内的一些研究者也开始对量子行为遗传算法进行了研究并取得了一定的成果[16-17]。本文亦是针对量子行为遗传算法的性能特点，将其应用于船体局部结构优化设计问题中，通过将结构设计变量进行离散化，并对多峰解空间进行随机搜索策略，采用二进制的量子比特编码操作和量子旋转门进行种群的个体更新调整，提高了算法的全局寻优能力与收敛速度，使其能够适应于船体复杂结构设计变量的优化问题。

1 船体局部结构优化参数的预处理

对于无约束优化问题，采用遗传算法来处理可以取得较好的全局最优解。然而对于有约束优化问题，若要获得较好的可行解，在求解问题前必须进行预处理，包括结构变量的离散化处理、约束条件的处理以及待优化目标函数的设定等。针对船舶设计中的某些结构变量，如果按照连续型变量进行求解，得到的最优解也是连续型的，这是不符合实际工程要求的，因为这种解不满足船体钢料型号尺寸的规格化要求；此外，在船舶主尺度的确定中，这种非圆整的最优解也是不便于设计建造的。对于上述问题文献[18]提出的一种混合整数规划法应用于船舶结构优化设计中，可以得到满足工程实用要求的最优可行解。在船体局部结构尺寸设计中，设计的变量既有连续型的又有离散型的；对于连续型设计变量，若结构变量的设计精度为δ，变量的上下限分别为u和l，则遗传算法的二进制码长度Nb可以按下式表示：

对于离散型设计变量，若令设计变量共有M个离散值，则所求的二进制串的长度K为

船体局部结构优化问题属于非线性约束优化范畴，一般可以按照如下方式来表达：

式中：x是决策设计变量，对于有连续型和离散型混合设计变量来说表示连续型设计变量集合，［xd］表示离散型设计变量集合；ui和li分别为设计变量xi取值的上下界限；f（x）为目标函数；）是第j个等式约束条件；和gj（x）是第j个不等式约束条件。

在采用遗传算法解决上述约束优化问题时，通常是先将其转化为无约束优化问题后再进行求解。目前比较常用的转化方法有抛弃法、修复法、遗传算子修改法和惩罚函数法等，本文应用惩罚函数法处理船舶结构优化中的非线性约束问题，详细方法在实验算例中给出。

待优化目标函数的设定是船体局部结构优化参数预处理中非常重要的一步，因为进行结构优化时目标函数要映射为遗传算法中的适应值函数，而适值函数又是算法构成的关键要素之一，它的大小将决定算法中选择和繁殖按照怎样的方式来进行。

2 船体局部结构变量优化的量子行为遗传算法

2.1 有关量子行为遗传算法的几个关键概念

（1）量子比特

在计算机中，把用0和1表示信息的二进制数称为比特。在量子计算中，则采用0〉和1〉分别表示微观粒子的两种基本状态（自旋向下态和自旋向上态），称为量子比特（quantum bit,qubit）[17]。量子比特是量子信息中最小的存储单元，符号“〉”称为狄拉克记号，它是量子力学的状态表示符。通常量子比特是被定义在二维复平面上的一个单位向量，它可以是状态的线性叠加，即

其中：α和β是复数概率幅对，并且量子叠加态φ〉还满足归一化要求：

（2）量子旋转门

在量子计算中，通过对量子比特状态进行一系列的酉变换可实现某些逻辑变换的功能，把这些实现逻辑变换的量子装置称为量子门。量子门的种类很多，根据其所起的作用可分为量子非门、相位门、π/8门、Hadamard门和量子旋转门等形式，其中量子旋转门是量子行为遗传算法中较常用的一种量子门，量子旋转门的定义为

其中：θ是旋转角度。

2.2 量子行为遗传算法的实现过程

量子行为遗传算法是量子计算和遗传算法相融合的产物，量子行为遗传算法也是需要进行概率搜索的算法，因而算法的第一步是初始化种群，种群中全部的染色体都是具有量子行为的基因，若用表示一条量子染色体，则

式中：m是量子位数；j=1,2,…,n，n是种群的规模；t是遗传代数。初始化时，所有的量子基因都被设置为，这就意味着一个量子染色体所表达的是其全部可能状态的等概率线性叠加：

量子行为遗传算法的具体求解流程如下：

（1）初始化种群及各个参数；

（2）对初始种群的各个个体进行测试；

（3）对确定解集中的每个解进行适应度评估；

（4）记录最优个体及其对应的适应度；

（5）确定计算过程的停止条件，如果满足停止条件就退出，否则进行下一步计算；

（6）对种群的各个个体再进行测试，获得相应的确定解；

（7）评价各个确定解的适应度；

（8）使用量子旋转门对种群中个体进行更新调整，更新过程是由（6）式来完成的，若和分别代表染色体第i个量子比特旋转门更新前后的概率幅，则

（9）记录下最优个体及其所对应的适应度值；

（10）转回到第⑤步判断计算过程是否停止条件。

3 实验算例及结果分析

为了说明采用量子行为遗传算法解决船体局部结构变量优化设计问题的有效性与可行性，本文采用三个有约束优化问题的算例来进行验证：（1）带约束条件的数值优化模型；（2）船体箱型剖面梁结构尺寸优化；（3）某油轮槽形横舱壁结构尺寸优化问题。

3.1 带约束条件的数值优化模型

求解如下约束优化问题：

要求解的目标函数曲面及约束函数曲面如图1所示。目标函数曲面是在x1坐标轴的负方向向下倾斜，由图示可见在约束条件下该目标函数的最小值点位于的面与圆柱面的交线上，而交线和目标函数曲面的交点就是所要求的最小值点，由目标函数曲面和约束函数曲面在设计变量平面上的投影线更能够看出，最小值点是采用传统数学优化方法所得结果如图2所示，最小值点是最小值是-37。

针对本算例，应用惩罚函数方法构造的适度值函数为

图1 目标函数曲面与约束函数曲面Fig.1 The objective function surface and the constraint function surface

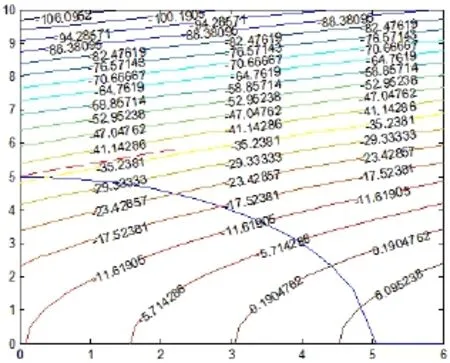
图2 函数优化结果Fig.2 The results of the function optimization

利用量子行为遗传算法优化时的初始参数设置是，种群规模N=50，二进制串码长度为l=20，最大遗传代数M=300，设计变量均为连续型变量，进行六次迭代计算结果如表1所示。

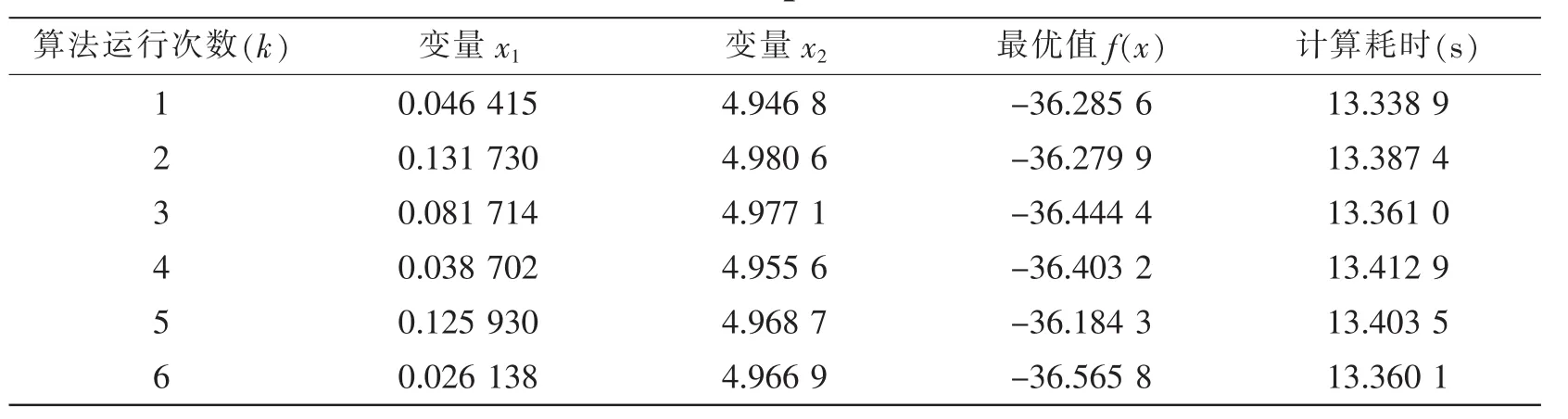
表1 数值优化结果Tab.1 Numerical optimization results

由表1可以看出，本文的优化结果在收敛精度上要好于传统数学方法的优化结果，而且计算时间也较短。

3.2 船体箱型剖面梁结构尺寸优化

铝质箱形舱口盖如图3所示[18]。箱形剖面梁结构的具体尺寸是，长l=600 cm，宽b=60 cm，腹板厚ts=0.5 cm；均布载荷为q=0.01 MPa；材料的弹性模量E=6.86×106N/cm2，泊松比μ=0.3，许用弯曲应力［σ］=7 000 N/cm2，许用剪切应力［τ］=4 500 N/cm2，梁的最大挠度δ=1.5 cm；求此箱形梁满足结构重量最轻时翼板厚度tf和腹板高度h的最优尺寸。

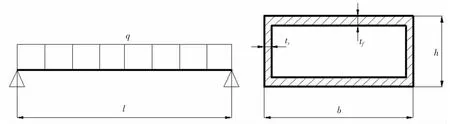
图3 箱型剖面梁结构Fig.3 The structure of the box beam profile

为了计算方便，令x1=tf，x2=h，那么该箱型剖面梁可以建立如下数学优化模型：

应用量子行为遗传算法优化计算时初始参数设置为，种群规模N=40，二进制串码长度为l=20，最大遗传代数M=200，设计变量均为连续型变量，进行六次迭代计算结果如表2所示。

表2 箱型梁剖面优化结果Tab.2 The optimization results of the box beam profile

本算例可进一步验证量子行为遗传算法在工程应用中的可行性和有效性。与文献[1，18]中的计算结果比较，本文提出的算法计算的收敛精度高，计算结果比较精确，剖面积优化结果也得到了降低，计算耗时也比较少。

3.3 某油轮槽形横舱壁结构尺寸优化

某65000W油轮的槽形横舱壁结构[1]如图4所示，按照CCS规范标准设计，求解该舱壁结构重量的最轻优化尺寸。

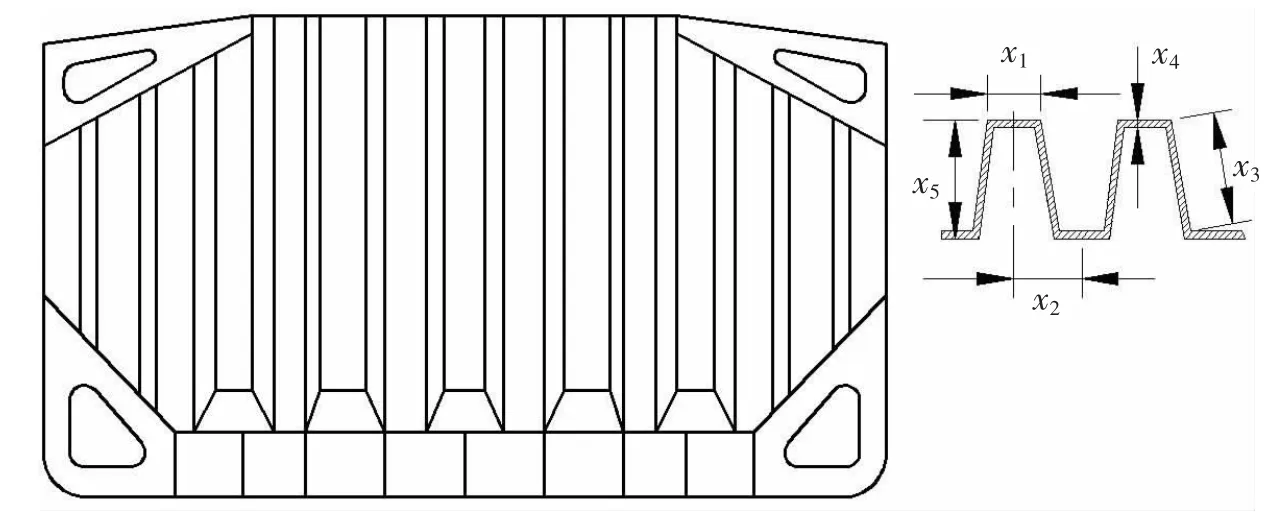
图4 某油轮槽形横舱壁结构Fig.4 An oil tanker’s transverse bulkhead structure

现以槽形舱壁板的五个结构尺寸参数作为设计变量，如图4右侧图所示。设x1为槽形壁的平板宽度，x2为平板的中心距长度，x3为斜板宽度，x4为舱壁板的厚度，x5为槽形平板的间距。采用CCS规范标准建立如下数学模型：

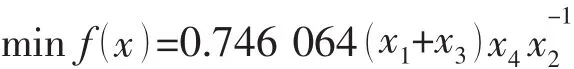
针对本算例并依据设计要求，这里设计变量按照混合型变量（即设计变量既有连续型的变量又有离散型的数值变量）来计算，假设槽形平板的间距x5取为连续型的数值变量，其余的设计变量均取为离散型的数值变量，如果参照文献[19]，则离散型数值变量可取如下值：

由于变量x1、x2、x3和x4是离散数值，且变量数量为8个，所以算法中二进制编码串的长度按（2）式计算，即

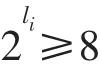
可得li=3。因而一个量子染色体的二进制编码可表达如下：

上式中假定连续型变量x5的二进制编码长度为15，则该染色体的二进制码串的总长度为

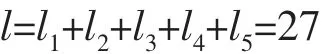
本算例采用惩罚函数法构造算法的适应度函数：

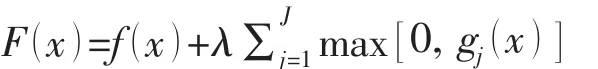
式中：λ是惩罚因子；J为约束总数。本算例的适度值函数具体表达形式如下：

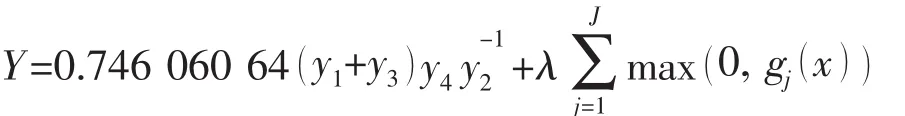
式中：惩罚因子取为λ=0.8；gj（j=1,2,…,7）分别是7个条件约束函数。

采用量子行为遗传算法优化计算时初始参数设置为，种群规模N=40，二进制串码长度为l=27，最大遗传代数M=200，算法运行六次后的优化计算结果如表3所示。

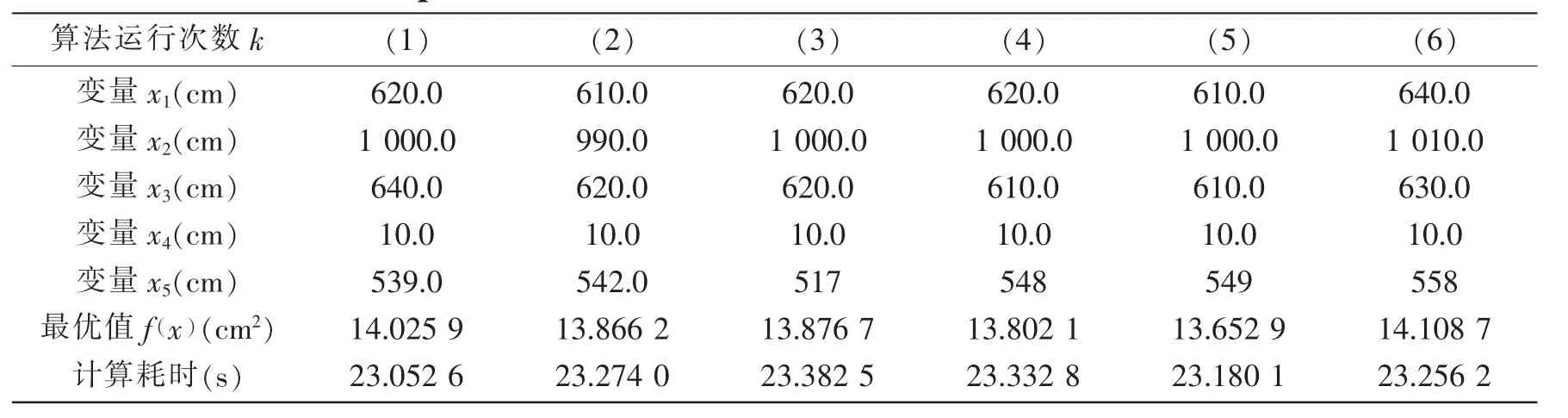
表3 某油轮舱壁结构优化结果Tab.3 The optimization results of an oil tanker’s bulkhead structure

针对本算例，应用量子行为遗传算法（QGA）与标准遗传算法(SGA)的进化过程如图5所示，由此可见QGA在收敛速度上要优于SGA，因此将量子计算同遗传算法相结合，可有效提高遗传算法的搜索性能。

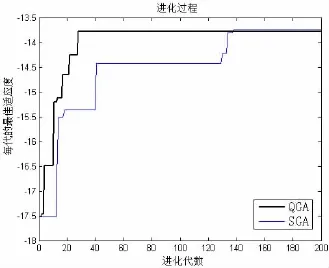
图5 QGA和SGA的进化过程Fig.5 The QGA and the SGA evolutionary process

4 结论

通过本文三个实验算例的验证，可见采用量子行为遗传算法对船体局部结构进行优化设计是可行的，且计算速度很快，特别是对于大型复杂结构的优化设计其效果尤为明显。3.3中的算例与3.1及3.2中算例的不同之处是3.3中算例既有连续型变量又有离散型变量，因而在构造适值函数时需先将离散变量列出来，所有的离散变量组合成一个离散数值矩阵，再由这个离散数值矩阵和QGA算法中的十进制编码矩阵再重组成一个映射矩阵。上述适值函数中的yi（i=1,2,3,4）就是映射矩阵中的元素。本文中的惩罚值对优化结果影响很小，经试算三个算例中的惩罚值均取0.8是比较合适的。

本文提出的算法基于标准遗传算法框架，采用量子计算的遗传编码策略，使用量子旋转门进行更新操作，可实现多种目标函数的优化求解。数值仿真及结构尺寸优化算例结果表明，量子行为遗传算法可以解决标准遗传算法能够求解的一切优化函数，并且不易陷入局部最优，求解质量和效率也比较稳定。此外，由于QGA算法以量子旋转门进行染色体的更新操作，故不需要像标准GA算法那样给出交叉概率和变异概率的初始设定值，因而也减少了算法参数的选择问题给实际计算结果带来的误差影响。

[1]徐昌文.结构模糊优化设计最优水平的确定[J].镇江船舶学院学报,1988,2(2-3)：39-48. Xu Changwen.The determination of the best level in fuzzy optimum design of structures[J].Journal of Zhenjiang Shipbuilding Institute,1988,2(2-3)：39-48.

[2]林焰,纪卓尚,李树范,王世连.船舶主尺度的模糊多目标规划设计[J].造船技术,1994,9：8-12. Lin Yan,Ji Zhuoshang,Li Shufan,Wang Shilian.Fuzzy multi-objective programming design on the main dimensions of ships[J].Shipbuilding Technology,1994,9：8-12.

[3]纪卓尚,林焰.船舶总布置设计专家系统的研究与进展[J].大连理工大学学报,1995,35(3)：380-383. Ji Zhuoshang,Lin Yan.Research and development for expert system of ship general arrangement[J].Journal of Dalian U-niversity and Technology,1995,35(3)：380-383.

[4]毛正良,张圣坤.人工神经网络在结构可靠性中的应用[J].上海交通大学学报,1997,31(11)：86-90. Mao Zhengliang,Zhang Shengkun.Applications of neural networks in structural reliability[J].Journal of Shanghai Jiaotong University,1997,31(11)：86-90.

[5]朱稣骥,顾学康,胡嘉骏.遗传算法的改进及其在超大型油船结构优化中的应用[J].船舶力学,2007,11(2)：237-249. Zhu Suji,Gu Xuekang,Hu Jiajun.Modification of genetic algorithm and its application in ship structural optimal design of a VLCC[J].Journal of Ship Mechanics,2007,11(2)：237-249.

[6]Gabor Renner,Aniko Ekart.Genetic algorithm in computer aided design[J].Computer Aided Design,2003,35：709-726.

[7]贺毅朝,王熙照,李文斌,等.基于遗传算法求解折扣{0-1}背包问题的研究[J].计算机学报，2015,38(133)：1-18.He Yichao,Wang Xizhao,Li Winbin,et al.Research on genetic algorithms for the discounted{0-1}knapsack problem[J]. Chinese Journal of Computers,2015,38(133)：1-18.

[8]陆晔,邵雄飞,俞铭华.基于蚁群算法的大型油船中剖面结构优化设计[J].江苏科技大学学报（自然科学版）,2007, 21(105)：10-14. Lu Ye,Shao Xiongfei,Yu Minghua.Optimization of mid ship section structure of large crude oil carrier based on ant colony algorithm[J].Journal of Jiangsu University of Science and Technology(Natural Science Edition),2007,21(105)：10-14.

[9]秦洪德,石丽丽.PSO算法在油船双底结构优化设计中的应用研究[J].哈尔滨工程大学学报,2010,31(8)：1007-1011. Qin Hongde,Shi Lili.Optimizing the design of the double bottom structure of an oil tanker using a particle swarm optimization algorithm[J].Journal of Harbin Engineering University,2010,31(8)：1007-1011.

[10]霍凤财,杜颖,刘洋.人工蜂群算法及其应用[J].吉林大学学报（信息科学版）,2016,34(4)：468-476. Huo Fengcai,Du Ying,Liu Yang.Artificial bee colony algorithm and its application[J].Journal of Jilin University(Information Science Edition),2016,34(4)：468-476.

[11]Aladahalli C,Cagan J,Shimada K.Objective function effect based pattern search theoretical framework inspired by 3D component layout[J].Journal of Mechanical Design,2007,129(3)：243-254.

[12]Pawan K S Nain,Kalyanmoy Deb.A computationally effective multi-objective search and optimization technique using coarse-to-fine grain modeling[C]//2002 PPSN Workshop on Evolutionary Multi-objective Optimization.Spain：Springer, 2002：2081-2088.

[13]Narayanan A,Moore M.Quantum-inspired genetic algorithms[C]//Proceedings of IEEE International Conference on Evolutionary Computation.Nagoya,Japan,1996：61-66.

[14]Han K H,Kim J H.Genetic quantum algorithm and its application to combinational optimization problem[C].Proceedings of the International Congress on Evolutionary Computation,IEEE Press,2000：1354-1360.

[15]Han K H,Kim J H.Quantum-inspired evolutionary algorithm for a class of combinational optimization[J].IEEE Trans Evolutionary Computation,2002,6(6)：580-593.

[16]Wang L,Tang F,Wu H.Hybrid genetic algorithm based on quantum computing for numerical optimization and parameter estimation[J].Applied Mathematics and Computation,2005,171(2)：1141-1156.

[17]李士勇,李盼池.量子计算与量子优化算法[M].哈尔滨：哈尔滨工业大学出版社,2009.

[18]纪卓尚,李树范,郭昌捷.船舶优化设计中的一个实用混合整数规划方法[J].大连工学院学报,1982,21(1)：69-76. Ji Zhuoshang,Li Shufan,Guo Changjie.An applied mixed integer programming method in ship design[J].Journal of Dalian University and Technology,1982,21(1)：69-76.

[19]曾广武.船舶结构优化设计[M].武汉：华中科技大学出版社,2004.

Optimal design of the ship hull local structure based on quantum-behaved genetic algorithm

LIU Boa,LIN Yana,LÜ Zhen-wangb,GUAN Guanb,JI Zhuo-shangb
(a.State Key Laboratory of Structural Analysis for Industrial Equipment;b.School of Naval Architecture and Ocean Engineering,Dalian University of Technology,Dalian 116024,China)

The optimization of the ship structure with the complex hybrid design variables based on genetic algorithm was introduced,its optimal result is very effective and the global best feasible solution is obtained.However,simple genetic algorithm has low efficiency in local extreme searching and might be easily premature.In order to enhance the global search ability in the complex solution space of ship structural design variables,a binary coded quantum-behaved genetic algorithm used for hybrid design variables optimization is presented in this paper,which is quite suitable for complex functions,and its search capabilities are better than the standard genetic algorithm.By three examples to test the efficiency and practicability of the algorithm,the experimental results show that quantum-behaved genetic algorithm enhances the quality of solution and shortens the consuming time.

quantum-behaved genetic algorithm;ship hull local structure;structural optimization design; hybrid design variable;global optimization ability

U662

A

10.3969/j.issn.1007-7294.2017.04.013

1007-7294（2017）04-0484-09

2016-09-29

国家公益性行业科研专项（201003024）；辽宁省教育厅科研项目（LS2010046）

刘波（1977-），男，博士研究生；林焰（1963-），男，博士，教授，博士生导师，E-mail：linyanly@dlut.edu.cn；纪卓尚（1938-），男，教授，博士生导师。