基于CARR模型对我国股指期货的非对称性研究

（西安建筑科技大学 理学院，陕西 西安 710055）

基于CARR模型对我国股指期货的非对称性研究

李少华，王建国

（西安建筑科技大学 理学院，陕西 西安 710055）

本文以沪深300股上证指数日收益率作为研究样本，在EGARCH模型的基础上，运用CARR模型对上证指数日收益率的非对称性进行预测和实证分析。结果表明，在运用CARR模型对波动率数据进行拟合的条件下，收益序列的波动特征呈现出杠杆效应，即收益率波动具有非对称性。

CARR模型；EGARCH模型；杠杆效应；波动率；收益率

金融(Finance)是一个国家经济发展、运行的核心，金融市场的发展情况可以体现出一个国家经济发展水平，研究金融市场波动规律是世界各国政府及金融机构共同的心声。在金融领域对于波动性的研究中，Parkinson(1980)提出了具有不变方差和连续时间参数的随机过程，并认为方差的高-低估计值比基于同样数目的观测值样本方差更为有效。在此理论方法基础上，Ray Y Chou(2005)提出了用极差去度量波动率的模型，即自回归条件极差模型（The conditional autoregressive range model,CARR）。

在我国,对CARR模型的研究相对较晚，程细玉,夏天等 (2009)做了金融市场波动性 CARR类模型与GARCH类模型的比较研究，发现CARR模型比GARCH模型对波动率的预测更有效。王沁(2017)研究了基于杠杆效应CARR模型的波动率预测，并对传统的CARR模型进行了修正，构造出具有杠杆效应的CARR模型。在此基础上，本文运用CARR模型对我国股指期货非对称性进行检验。

一、CARR模型结构分析

为了将股市期货日收益波动的对称性特征描述得更加具体，我们在讨论CARR模型的非对称性之前，先回顾一下EGARCH模型结构，在此我们只对EGARCH(1,1)模型进行讨论，如下：

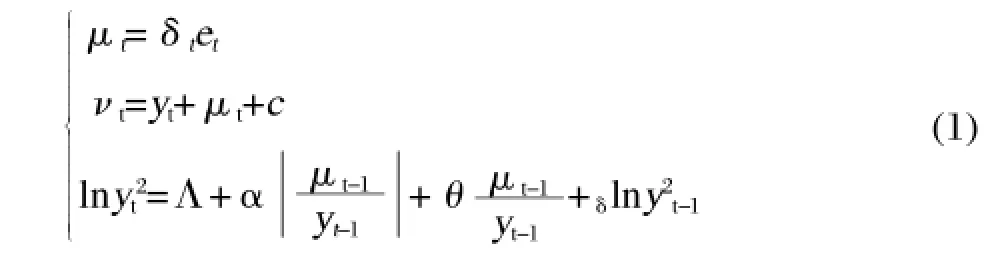
在此理论基础上，我们接下来讨论CARR(m,n)模型，模型结构如下：

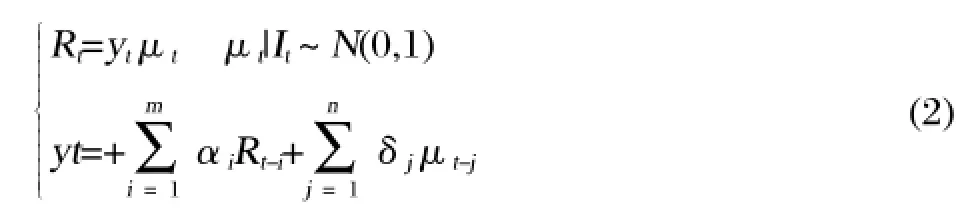
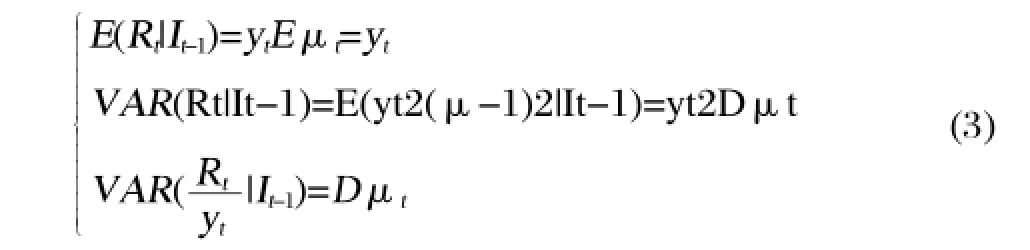
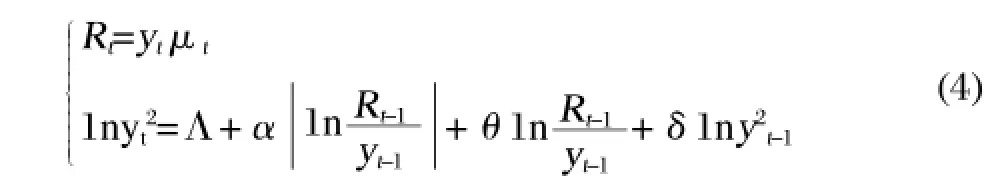
综上，有

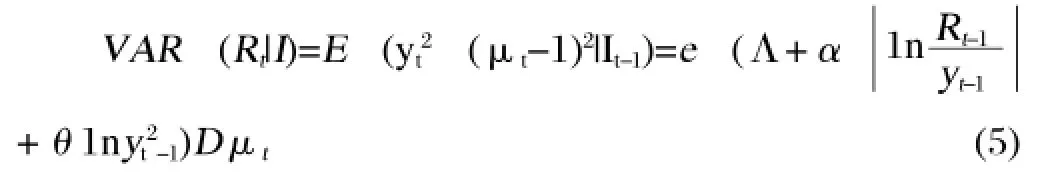
实证分析

1、数据的选取

本文数据来源于中国金融期货交易所，选取CSI300指数2014.1.13日至2016.12.22日的日收盘价作为样本数据，其中数据不包含周末与节假日，共选取768组数据作为样本数据。

我们以CSI300指数的日收盘价为依据，计算其对数收益率，即，其中表示对数收益率与分别表示第 日与第-1日的CSI300指数的日收盘价。下面我们将用Eviews9.0和Excel软件对模型进行实证检验，通过运用Eviews9.0软件我们得到对数收益序列的直方图与描述统计量(如图1)及带有趋势项的金融时间序列图(如图2)。

表1 沪深300股指期货指数日收益序列描述性统计特征

2、统计特征

通过对CSI300指数的日收益率进行统计分析，我们得到了表1，在表1中我们给出了收益率的均值(Mean)、最值(Max&Min)、标准差(Median)、偏度(Skewness)、峰度(Kurtosis)及Jarque-Bera统计量。

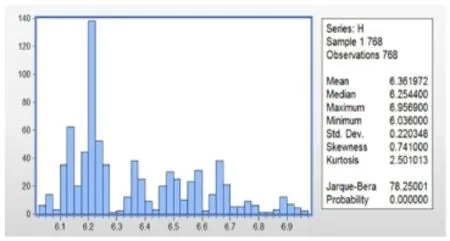
图1 对数收益序列的直方图与描述统计量

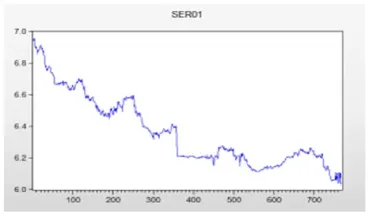
图2 带有趋势项的金融时间序列

分析图表易知，收益率的偏度大于零，峰度约为3，说明收益序列呈现尖峰、后尾现象。JB统计量为78.2501，000000，说明此统计特征不服从正态分布。这些特征说明我国股指期货市场存在波动聚集效应，因此用传统正态分布假设检验去估计期货市场的波动往往与实际存在较大偏差，对投资机构及金融部门造成金融风险，所以对我国股指期货方面的研究应采用非对称性的建模思想进行研究。

对于股指期货日收益率的处理，采用杠杆效应的CARR模型对其进行拟合，下面是通过进行实证检验，模型分析如表2。

分析CARR模型的参数可以看出，收益率序列的均值和极差都具有时变性，参数=-0.133927＜0，说明股市价格呈现波动特征，即杠杆效应，这种特征使得我国股指期货市场的收益率呈现出非对称性。

表2 沪深300股指期货指数日收益序列CARR模型分析

三、结论分析

本文运用CARR模型分析了我国股指期货市场的波动性和非对称性，并且对我国股指期货非对称性进行检验。主要结论有以下两方面：

（1)条件自回归极差的存在性，即收益序列呈现尖峰、后尾现象。

（2）我国股指期货收益率下跌程度通常高于收益率上涨程度，即股指期货的收益率存在非对称性。

[1]Alessandro Rossi,Giampiero M.Gallo.Volatility Estimation via Hidden Markov models[J].Journal of Empirical Finance,2006,13: 203-230.

[2]Parkinson M.The Extreme Value method for estimating the variance of the rate of return[J].Journal of Business,1980(53): 61-65.

[3]Ray Y Chou.Forecast Finance Volatilities with Extreme Values[J].Journal of Money,2005(67):34-56.

[4]程细玉、夏天：金融市场波动性CARR类模型与GARCH类模型的比较研究[J].数学实践与认识,2009,39(13):12-18.

[5]王沁：基于杠杆效应CARR模型的波动率预测[J].数理统计与管理,2017,1(36):51-58.

（责任编辑：闫涛涛）