导弹多点激励振动试验系统动力学仿真

王肇喜，王海东，王国顺，仇原鹰，陈燕云

（1.上海航天精密机械研究所，上海201600；2.西安电子科技大学机电工程学院，西安710071）

导弹多点激励振动试验系统动力学仿真

王肇喜1，王海东1，王国顺1，仇原鹰2，陈燕云2

（1.上海航天精密机械研究所，上海201600；2.西安电子科技大学机电工程学院，西安710071）

基于一种闭环控制方法，对导弹多点激励振动试验系统进行动力学仿真。通过对整个系统进行合理简化，利用MSC.Patran/Nastran有限元软件对振动试验系统进行模态分析及随机振动分析。最后，计算出各控制点的振动加速度响应谱。结果表明，试验结果与仿真结果基本一致，验证了计算机动力学仿真的正确性。

振动与波；导弹；多点激励；闭环控制；有限元分析；MSC.Patran/Nastran

目前国内航空、航天等领域中振动试验主要用到单振动台以及双振动台试验系统[1]。但是由于单振动台激振力不足并且只能沿单一方向进行激励，为了更加真实地模拟实际振动环境，文中采用多振动台进行多点激励振动试验[2]。多点激励振动试验系统的控制技术也是该领域的热点，控制系统分为开环和闭环两种，然而开环控制系统受到非线性因素的影响，得到的响应结果与目标值有很大的误差，闭环控制可以对偏差进行修正，所以需要采用闭环控制，使系统的响应逼近目标信号[3]。

多点激励振动试验系统结构的复杂性大大提高了试验成本和效率。为了给振动试验提供可靠的参考以及减少试验次数，在试验前引进振动试验环境下的仿真运算是相当必要的[5-8]。在结构动力学仿真方面，MSC.Patran/Nastran是功能强大、应用广泛、通用的大型有限元分析软件，其运算结果被业界所认可，因此能够对试验结果起到预测作用[9]。文中基于闭环控制方法，利用MSC.Patran/Nastran有限元软件对导弹多点激励振动试验系统进行动力学仿真。

1 多点激励振动试验系统控制原理

1.1 载荷识别

多点激励振动试验系统的物理模型可以简化为多输入多输出（MIMO）系统[4]。若假设试验系统中有m个激励谱x(ω)输入，n个控制谱y(ω)输出，那么每一个激励将对所有的控制响应产生作用，驱动信号与控制信号之间的关系可描述为

矢量形式为

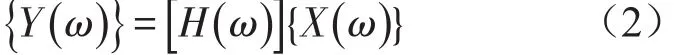
式中{Y(ω)}是系统的输出控制谱矢量；{X(ω)}是系统输入激励谱矢量；[H(ω)]是试验系统的频响矩阵。

多点激励振动试验的目的是使输出的响应与用户规定的参考信号在误差允许的范围内一致，这就需要对系统进行解耦，确定所需的激励，根据式（2）得

若n个输出控制谱已知，即可反求所需加载的m个激励谱。当m=n时，即激振力个数与控制测点个数相同时，对方阵求逆可以得到激励谱的唯一解；当m＜n时，即激振力个数小于控制测点个数时，对矩阵求广义逆可以得到激励谱的最小二乘解。若试验系统是线性的，用式（3）开环控制产生响应就能达到目标信号的要求。但由于系统非线性因素的存在，得到的响应与目标信号存在很大误差，采用闭环控制，就能使系统的响应逼近目标信号。

1.2 控制方法

（1）方阵控制机理

控制测点的个数等于激振力的个数的控制方式为方阵控制。方阵控制中逆问题求解时求解激振力的方程组为方阵，可直接计算激振力的唯一解，即可以得到使控制点的实际振动响应谱与预设的控制谱完全一致的激振力。

（2）长方阵控制机理

控制测点的个数大于激振力的个数的控制方式为长方阵控制。长方阵控制中逆问题求解时求解激振力的方程组中，因方程的个数大于未知数的个数成为超越方程组，这种方程组一般情况是无解的，可以求其最小二乘解（最小范数解）。

2 导弹多点激励振动试验系统有限元建模

导弹多点激励试验系统包括电动振动台、夹具、球头支撑以及导弹四部分组成。电动振动台包括骨架和线圈上下两部分；夹具用来连接导弹和球头支撑；球头支撑上端与夹具固定连接，下端与电动振动台台面用螺钉固定连接，用来传递激振力；导弹一共有五个舱段，各舱段之间通过螺栓连接。

2.1 几何模型与有限元模型

分别采用Pro/E[10]和MSC.Patran创建几何模型与有限元模型。由于导弹多点激励振动试验系统模型的复杂性，加剧了建模的复杂性，同时也增加了有限元网格划分的单元数量和节点数量，为了提高计算效率，需要对导弹几何模型进行简化。考虑到模型的复杂性，使用四面体十节点单元进行网格划分。导弹多点激励振动试验系统几何模型与有限元模型如图1（a）所示。

2.2 建模时的处理

在实际工作中，动圈通过靠近台面上部的8个U型弹簧挂在刚性台体上，台体与地面刚性连接。以上连接使得整个动圈在低频运动时表现出来的自由度只有竖直Z向。导弹通过绳索悬挂以抵消自身重力。

在有限元中模拟时，对U形簧所在位置的四周仅保留Z向平动自由度，如图1（a）所示；中心圆柱轴为导向装置，同样保留Z向平动自由度，如图1（b）所示；圆柱轴底部连接有弹簧单元，弹簧单元底部完全约束如图1（c）所示。悬挂杆上部端面需要完全约束。

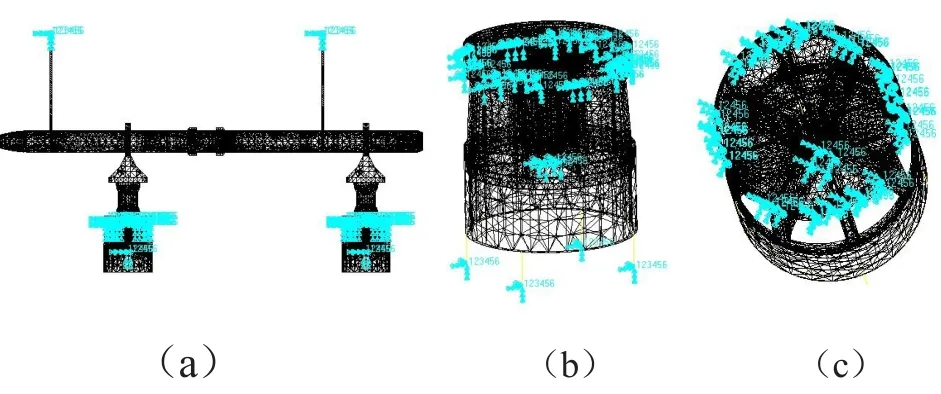
图1 有限元模型及边界条件模拟情况

2.3 材料及属性的定义

动圈分为两部分：骨架和驱动线圈。动圈几何模型上部为骨架，由镁铝合金整体浇铸而成，驱动线圈主要材料为结构钢；工装夹具的材料为铝镁合金；静压轴承材料为结构钢；导弹除发动机舱是钢之外，其它部件都是钛合金。

3 导弹多点激励试验系统模态分析

模态分析的主要目的和任务是求解系统的固有频率和固有振型。只有了解了系统的自身振动特性，才能有效地研究动力学响应问题。

利用MSC.Patran提供的模态分析模块，对导弹多点激励振动试验系统进行Y向（竖直方向）空载模态分析。模型修正[11–15]后导弹多点激励试验系统固有频率和模态振型如下：

由导弹多点激励试验系统固有频率和模态振型图可以看出，导弹多点激励振动试验系统模型的计算频率和振动台模态试验结果吻合较好，最大误差不大于5%，达到了仿真计算的目的。

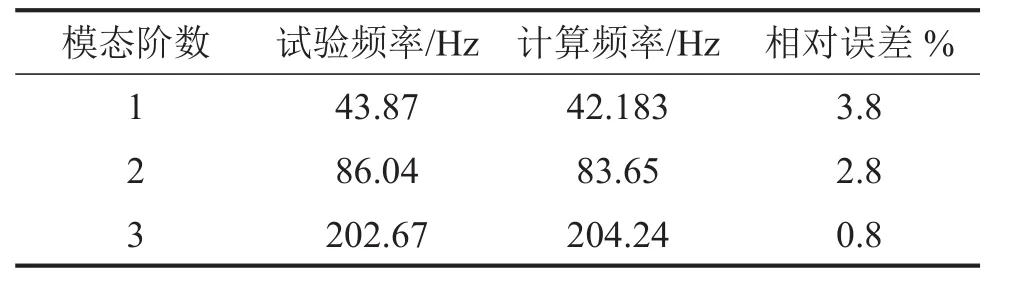
表1 导弹多点激励试验系统固有频率

4 导弹多点激励随机振动试验仿真

4.1 导弹多点激励振动试验方案

（1）导弹多点激励振动试验系统的安装方式

全弹水平吊装，采用双台激励方式，夹具与振动台球头连接，导弹通过夹具与振动台刚性连接。导弹多点激励振动试验系统共安装14个传感器，传感器测点位置如图3所示。

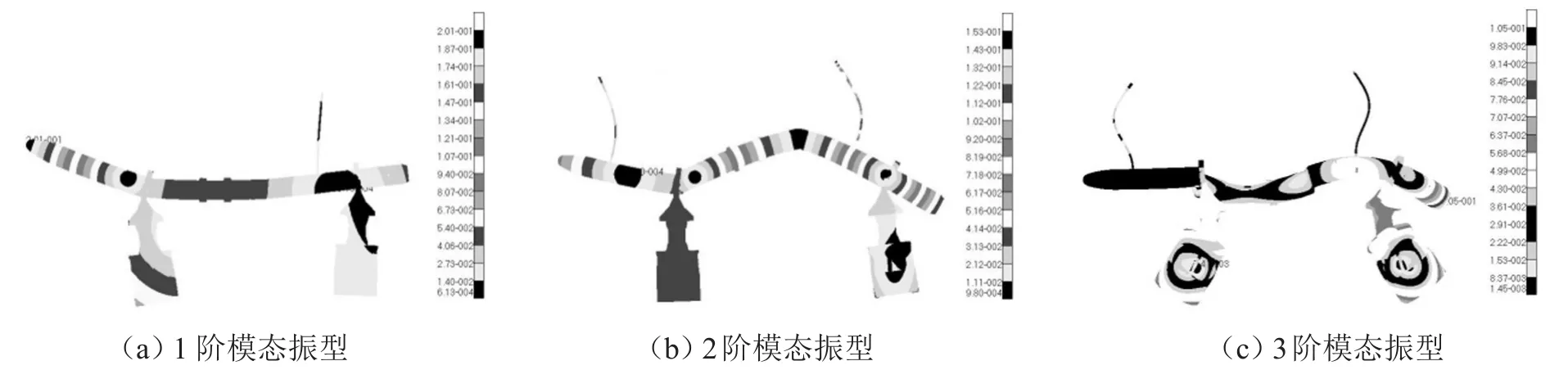
图2 导弹多点激励试验系统前3阶模态振型图

图3导弹多点激励系统加速度传感器安装示意图

图3中，除CH5、CH6、CH10和CH11为控制点外，其余均为监测点。两个控制点使用方阵控制，两个以上控制点使用长方阵控制。

（2）导弹多点激励随机振动试验仿真的技术路线

技术路线如图4所示。首先，对导弹结构进行模型简化及修复；其次对结构进行模态分析；最后分别在m个输入处加载单位白噪声激励功率谱，利用有限元软件获取第r(r=1，2，…，m)个输入处单独加载白噪声激励时，n个输出控制点处的响应功率谱。将以上数据代入载荷识别理论式（3），根据预设的n个输出梯形控制谱，即可求得需要施加在m个输入处的基础加速度载荷谱。然后将基础加速度载荷谱加载在对应的夹具底部，得到n个输出控制点的实际加速度响应功率谱密度函数，再与预设的加速度功率谱密度函数对比，进行相对误差分析。

4.2 导弹多点激励随机振动试验在MSC.Patran中的实现

基于MSC.Patran的导弹多点激励随机振动试验仿真[16–18]具体步骤如下：

图4 导弹多点激励随机振动试验仿真的技术路线图

（1）确定各点激励和响应之间的频响函数

在MSC.Patran中建立有限元模型，并利用MSC.Nastran对结构进行频率响应分析，确定各点激励和各点响应之间的频响函数。

（2）求解基础激励

选定响应控制点处的预设谱如图5所示，结合载荷识别理论式（3）及频响函数的有限元分析结果，求解激励点的基础载荷谱。

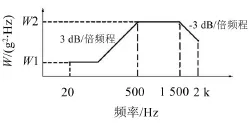
图5 头尾部预设谱谱型

（3）获取各控制点的响应谱

将计算得到的基础激励施加到结构有限元模型上，应用MSC.Patran随机振动分析模块求解结构上任意结点处的响应功率谱密度（PSD）函数、响应均方根（RMS）值，并输出结果，绘制结果曲线，图6和图7分别为控制点CH5与CH10的响应。

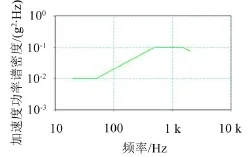
图6 头部控制点CH5功率谱密度曲线

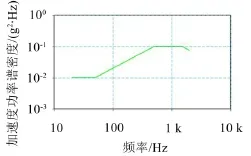
图7 尾部控制点CH10功率谱密度曲线

经计算分析，仿真计算结果与预设谱具有较高的吻合度，各控制点的相对误差在合理范围内，说明该工况为较优的一种组合，可以有效指导实践。

5 结语

旨在面向导弹多点激励振动试验系统的工程实际，利用MSC.Patran建立可靠的振动试验系统有限元模型，。基于一种闭环控制方法，进行随机振动试验仿真，可以有效地指导实际试验中各点的响应情况。

[1]王磊，王飞，王海东，等.细长型飞行器双台随机振动试验虚拟试验技术研究[J].上海航天，2014(1)：1-2.

[2]尹浩庆.随机基础激励响应控制及Patran的二次开发[D].武汉：华中科技大学，2011.

[3]陈家焱.多点激励振动试验系统的控制策略研究［D］.杭州：浙江大学，2011.

[4]陈家焱，王海东，周建川，等.多点激励振动试验控制技术进展［J］.振动与冲击，2011，30(3)：69-73．

[5]宦海祥.电动振动设备的发展及展望[J].环境试验，2006(4)：28-31.

[6]范宣华.电动振动台建模与试验仿真技术研究[D].北京：中国工程物理研究院，2005.

[7]朱元夫.系统级产品振动试验仿真[J].强度与环境，2003，11(4)：59-62.

[8]侯瑞，陈国平.振动台虚拟试验的建模和仿真研究[J].力学季刊，2008，29(2)：254-258.

[9]龙凯，贾长治，李宝峰.Patran 2010与Nstran 2010有限元分析从入门到精通[M].北京：机械工业出版社，2011.

[10]胡仁喜.Pro/ENGINEER Wildfile[M].北京：清华大学出版社，2004.

[11]王金明，李伟明，彭明峰.基于ICMC法的GARTEUR结构有限元模型修正研究[J].振动与冲击，2011，30(5)：90-95.

[12]GUYAN R J.Reduetion of stinffess and matrlces[J]. AIAAJ,1965(3):380-385.

[13]ANDESRON L R,HALLAUER JR W L.A method of order Reduetion for Structual Dynmaics[J].AIAAJ,1981 (6):796-800.

[14]MOOER B C.Principal component analysis in linear systems.conirollability,obsevrabiliy and model reduetion [J].IEEE Trans.onAutom.Conrtol,1981(l):17-32.

[15]O’CALLHANA J C.Comparison of Reduced Model. Conference[C].Procofthe8thInternationlModel Analysis Conference,1990:442-430.

[16]华明海.关于随机振动试验[J].环境技术，2009，2(1)：42-52.

[17]XIAO Q,ZHU H.Random vibration analysis of dynamic characteristics of tall building structure based on power spectral density of wind pressure method[J].Industrial Construction,2009,39:71-73.

[18]ARONE R A,BROCK P A.Control technique for multiple-shakervibrationsystem[J].Shockand Vibration Bull,36,Pt 3,1967:147-155.

Dynamics Simulation of Vibration Test System for Missile’s Multi-point Excitation

WANG Zhao-xi1,WANG Hai-dong1,WANG Guo-shun1,QIU Yuan-ying2,CHEN Yan-yun2
(1.Shanghai Spaceflight Precision Machinery Research Institute,Shanghai 201600,China; 2.School of Electromechanical Engineering,Xidian University,Xi’an 710071,China)

Based on a closed loop control method,the dynamic simulation of a vibration test system for multipoint excitation of missiles is carried out.Through the reasonable simplification of the whole system,the modal analysis and random vibration analysis of the vibration test system are carried out by using the MSC.Patran/Nastran finite element software.Finally,the response spectrum of the vibration acceleration of each control point is calculated.The results show that the test results are consistent with the simulation results,which verifies the correctness of the computer dynamic simulation.

vibration and wave;missile;multi-point excitation;closed loop control;FEA;MSC.Patran/Nastran

TB53；TU312；O32

A

10.3969/j.issn.1006-1355.2017.02.011

1006-1355(2017)02-0053-04

2016-11-14

航天八院核心攀登工程资助项目（ZY2013-004）

王肇喜（1986－），男，工程师，主要研究方向为振动、冲击等试验技术。

陈燕云，男，研究生。E-mail:cyyun2016@163.com