轴箱对轨道不平顺的响应及其可测性分析

方格，吴天行，彭志科，王誉蓉

（上海交通大学机械系统与振动国家重点实验室，上海200240）

轴箱对轨道不平顺的响应及其可测性分析

方格，吴天行，彭志科，王誉蓉

（上海交通大学机械系统与振动国家重点实验室，上海200240）

轨道不平顺会加剧轮轨的动态作用，引起轮轨部件损坏、噪声等问题，一直是铁路维护工作的重点。考虑到维护的成本，对轨道不平顺程度的实时监测显得尤为重要，其中轴箱加速度信号的二次积分是使用较多的方法。然而轴箱加速度包含的成分复杂，为了更深入地认识轴箱加速度的测量结果，建立多车轮与轨道相互作用模型，详细分析轨道不平顺激励下的轴箱与转向架的动态位移响应，重点关注轴箱响应对轨道不平顺的可测性，并给出了扩大测量频率范围的建议。结果显示：低频（长波长）情况下轴箱对轨道不平顺的响应接近理想，但是高频的位移响应受到多车轮耦合作用的影响，呈现很大的不确定性。

振动与波；轨道不平顺；轴箱加速度；多车轮作用；驻波

钢轨不平顺是车辆和轨道振动的主要激振源，严重时会导致钢轨以及车辆部件受损和轮轨噪声等问题，因而一直是轨道维护的重点对象。维护策略的制定依赖于轨道表面状态的检测。目前测量较短波长的不平顺主要采用手推式轨检车[1]，但是它不适合用来测量长波长的不平顺。为了实现对钢轨不平顺的长距离检测，列车正常运营状态下的轴箱加速度信号成为研究热点[2–4]。

采用装在运营车辆上的惯性传感器如加速度计和陀螺仪来测量钢轨不平顺由于设备简单、鲁棒性强，引起了国内外学者的广泛关注。Weston使用轴箱加速度计和转向架陀螺仪来测量轨道的垂向不平顺，并考虑了速度对二次积分的影响[5]。Lee提出了一种混合滤波的方法，将加速度信号的滤波和积分过程综合起来考虑[6]。Tsunahinma和Naganuma运用卡尔曼滤波的方法根据车体的加速度信号得到钢轨不平顺[7]。Li通过有限元模拟方法得到轮轨系统的动态特征，并基于此提出采用轴箱加速度计检测轨道局部缺陷的算法[8–9]。这些方法本质上都是基于车轨系统在钢轨不平顺激励下的动态响应，因而事先仔细分析响应特性对测量结果的理解和具体算法的设计都尤为重要。

Wei采用整车模型分析转向架和车体的响应，但是未考虑轨道的振动[10]。Grassie分析单个车轮与轨道作用时轴箱加速度的响应特性，但是此模型未考虑多个车轮耦合作用的影响[11]。本文旨在弥补已有结论的不足，考虑多车轮与轨道的相互作用，得到更完善的车辆系统位移响应特性，以指导钢轨不平顺的测量。

基于Wu的多车轮模型，推广单车轮作用下轴箱位移与钢轨不平顺间的响应关系，可得到多输入多输出形式的响应关系[12]。通过数值计算分析多车轮作用下轴箱位移响应的主要性质，重点关注轴箱位移响应对轨道不平顺的反应情况，提出可以改善测量效果的建议，得到的结论有一定的参考价值。

1 车辆-轨道耦合动力学模型

1.1 多车轮与轨道作用

多个车轮与轨道相互作用的模型如图1所示，仅考虑垂向运动，车轮、轨道位移以及钢轨不平顺均以向下为正。该模型只是为了表示轮轨的作用关系，车轮以上的转向架和车体部分以及轨道以下的支撑部分均未显示。

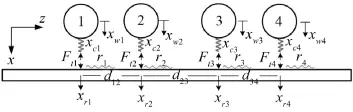
图1 多车轮与轨道相互作用模型

假设车轮与轨道始终保持接触，那么车轮和轨道的位移满足如下的约束关系

其中xw=[xw1xw2xw3xw4]T和xr=[xr1xr2xr3xr4]T分别代表四个车轮和轨道在四个车轮处的位移向量，xc=[xc1xc2xc3xc4]T表示四个轮轨接触赫兹弹簧相对平衡位置的压缩量，r=[r1r2r3r4]T是钢轨不平顺向量。

将轨道的动柔度矩阵记为αr=[αrij]4×4，其中元素αrij代表在车轮j处作用单位简谐力，轨道在车轮i处的位移响应。同样的，四个车轮以及对应的接触弹簧的动柔度矩阵可以定义为αw=[αwij]4×4和 αc=[αcij]4×4。根据图1不难看出αc不存在交叉项，是对角阵。但是轨道动柔度存在交叉项，意味着不同车轮间存在耦合关系，这是与单轮作用的区别所在。动柔度的具体计算方法将在后续部分详细介绍。

将四个车轮处的轮轨作用力记为Ft=[Ft1Ft2Ft3Ft4]T，则可以得到车轮、轨道位移以及接触弹簧的形变量分别为xw=-αwFt,xr=αrFt,xc=αcFt.代入式(1)，可以得到车轮位移作为输出和钢轨不平顺作为输入的响应关系。

实际上，根据轮轨作用力表达式（3），也可以方便地计算出其他输出如转向架位移xb、轨道位移xr与钢轨不平顺输入的响应关系，如

其中αb为转向架动柔度矩阵，其元素αbij代表在车轮j处作用单位简谐力时，转向架i的位移响应。

考虑到不同车轮处的钢轨不平顺输入实际上是同一个激励源，只是满足时间滞后关系，可以将输入矩阵记为

其中，d12、d13和d14分别代表轮1到轮2、3、4的距离，r代表不平顺幅值，V是车辆的运行速度。

1.2 普通有碴轨道和地铁减振轨道模型

普通有碴轨道的模型如图2所示，轨道用无限长的铁木辛柯梁来模拟，轨垫和道碴都用粘性弹簧单元来近似，不考虑它们的质量。轨枕抽象为集中质量块。轨道系统的动力特性由以下特征参数决定：扣件的刚度kp、道碴的刚度kb、轨枕的质量ms、轨枕间距d。

图2 有碴轨道

地铁的减振轨道模型如图3所示，由于扣件的刚度远远小于非碎石道床的刚度，所以这里不考虑道床的变形，将钢轨下的离散支撑等效为单层的弹簧阻尼单元。

为了计算无限长轨道的动柔度，只考虑有限个数的轨下支承，用Ns表示。因为在离激励点较远处，轨道的振动将明显衰减，所以这种简化是合理的。轨道的动柔度可以表示为

图3 地铁减振轨道

其中α,αr分别代表自由轨道和有支承轨道的动柔度，(z,z0)表示单位简谐力的激励点位于z0处，响应点位于z处。自由轨道的动柔度可以根据铁木辛柯梁理论求得。Zs代表支承的动刚度，即支承点向下运动单位位移对轨道产生的反作用力，有碴轨道可用下式表示

地铁减振轨道的支承动刚度则为

ui是各支承点处的轨道位移，可以通过求解以下的线性方程组得到

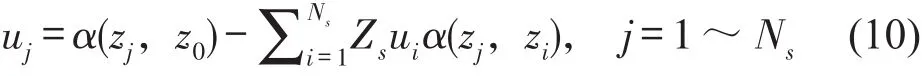
轨道的动柔度不仅跟激励点和响应点间的距离有关，还跟激励点的位置有关。

CHN60钢轨的相关参数为：材料密度ρ=7 850 kg/m3，弹性模量E=2.1×1011(1+0.01i)N/m2，截面面积A=7.745×10-3m2，截面惯性矩I=32.17×10-6m4，剪切模量G=0.77×1011N/m2，剪切系数к=0.4。

1.3 车辆模型

车辆部分采用的模型如图4所示，包括相邻的两个转向架，车体部分等效为集中质量，这是因为车辆存在悬挂阻尼，而且一节车厢很长，衰减了车轮和转向架振动通过车体部分的耦合作用。由于本文主要关注车轮和转向架位移对轨道不平顺激励的动力响应，所以车体部分作简化处理。另外，两个转向架分别位于相邻两个车厢，因为它们之间的距离比较小，耦合作用更明显。初级悬挂和次级悬挂都用黏性弹簧来近似，车轮等效为集中质量。

图4 车辆模型

如图所示，车辆部分总共包含10个自由度，分别是车体、转向架、车轮的垂向运动以及转向架的俯仰运动。求解其运动方程，可以得到车轮位移与轮轨作用力间的函数关系：

其中Jb是转向架的俯仰转动惯量，Lb是转向架的半轴距，kc1和kc2分别是两级悬挂的刚度，mb、mc和mw分别代表转向架、车体和车轮的质量。车轮的动柔度可以表示为

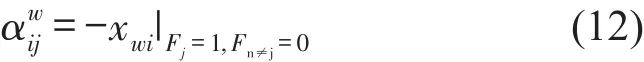
其中αwij的下标表示在轮j处作用单位简谐力时轮i处的位移响应。

同样地，可以得到转向架动柔度

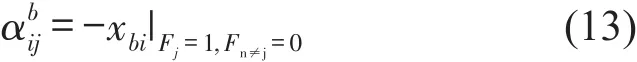
车辆部分相关的计算参数如下：Jb=1 205 kg∙m2，Lb=1.25 m，kc1=828 kN/m，kc2=1 500 kN/m。赫兹弹簧的刚度为kH=1.3×109N/m，其动柔度即αc=1/kH。

2 轴箱与转向架位移响应分析

2.1 轴箱和转向架响应

轴箱（车轮）位移响应可根据式(4)计算。图5显示了地铁减振轨道上车轮1的位移相对于轮1处钢轨不平顺的频率响应曲线。

图5 在地铁减振轨道上车轮1的位移响应

在频率较低(小于80 Hz)时，多轮模型的结果与单轮模型相同，这是因为轨道在低频段的振动衰减率较大，车轮间的耦合作用不明显。在34 Hz处出现第一个共振峰，此时车轮和轨道一起在轨道下的支承弹簧上共振。当频率低于15 Hz时，车轮的位移基本是跟随轮1处的钢轨不平顺。假设地铁的运行速度为15 m/s、10 m/s，就可以采用轴箱响应测量波长大于1 m、0.67 m的钢轨不平顺。相反，在频率较高（大于80 Hz）时，多轮模型得到的车轮位移响应会在单轮模型的结果上不规律的波动。这是因为高频段钢轨衰减率低，轨道振动波在车轮间反射叠加，导致不同车轮间存在耦合。当反射波与发射波相位差为0时会形成驻波，引起车轮的共振。高频范围的不确定性使得采用轴箱响应测量短波长不平顺十分困难。

转向架垂向位移响应可根据式(5)计算，考虑到转向架的俯仰运动，图6中计算了不同位置处（转向架中心和两端，见图4)的位移响应。

图6 在地铁减振轨道上转向架1的垂向位移响应

在频率小于1 Hz时，两者基本重合，而且完全跟随钢轨不平顺的变化。转向架中心的位移响应呈现周期性的波谷，第一个出现在3 Hz，频率间隔为9 Hz，对应车速15 m/s的波长为2.5 m，正好是转向架的轴距，这些频率点处轮1和轮2处的钢轨不平顺正好反向，因而俯仰运动显著。转向架两端的位移响应相对更加平稳，但是仍然会受到这种效应的影响。在高频范围，转向架的位移响应同样呈现很大的不确定性，这些因素导致装在转向架上的传感器测量范围更窄。

图7和图8分别表示有碴轨道工况下的车轮和转向架的位移响应。低频范围的趋势与减振轨道相同，但是车轮响应的第一个共振峰出现在52 Hz，此时车轮、轨道和轨枕一起在道碴弹簧上共振。

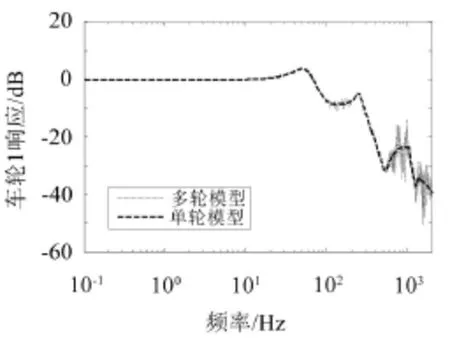
图7 在普通有碴轨道上车轮1的位移响应

因为道碴的刚度比减振轨道的支承刚度大，导致共振频率大，因而使得车轮的位移响应在小于35 Hz的频率段内都接近理想。高频情况下，与地铁减振轨道相比，多轮模型的车轮响应相对于单轮模型的波动比较小，这是因为有碴轨道的阻尼更大，更能有效衰减轨道振动波，从而车轮间的耦合作用相对减弱。

图8 在普通有碴轨道上转向架1的垂向位移响应

2.2 多车轮的耦合作用

从前面的位移响应结果不难看出，高频范围内多车轮模型的结果与单车轮模型有很大差别。为了进一步理解多车轮的耦合作用，这里考虑两个车轮与地铁减振轨道相互作用的情形。只考虑轮1处的不平顺，那么轮2对轮1的影响只能通过轨道振动波在轮2处的反射实现。

钢轨不平顺向量为r=[1 0]Tr，根据式（4），可以得到车轮的位移如下

两个车轮间的轨道位移响应可以按下式计算

其中z=0表示轮1所在位置。

车轮1的位移响应如图9所示，可以看到在150 Hz、355 Hz、625 Hz和930 Hz处均出现峰值，其中625 Hz处尤其显著，这只可能是轨道振动波在两个车轮间反射叠加后形成驻波引起的。

图9只考虑轮1处的钢轨不平顺时车轮1的位移响应

图10显示了图9中对应峰值频率处的轨道位移响应，其中横坐标为轮1和轮2间的轨道位置。图中显示的实际上是轨道在两轮间的振型。不难看出，150 Hz、355 Hz、625 Hz和930 Hz情况下两轮间的结点数分别为0、1、2、3，两轮间轨道的振型近似包含1、2、3、4个半波长，说明在这些频率点处确实形成了驻波。

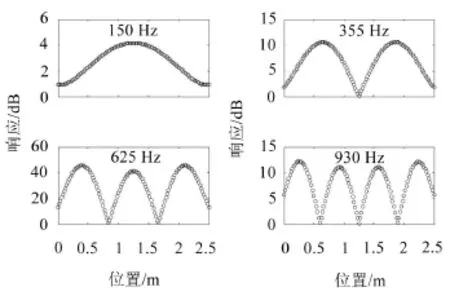
图10 两轮间的轨道位移响应(驻波)

当轮1和轮2下的钢轨同时存在不平顺时，有些频率处轨道振动波会通过叠加增强，而有些却被抵消，导致高频范围的车轮响应呈现明显的不确定性。

3 基于轴箱加速度的测量

3.1 可测性分析

从车轮位移对钢轨不平顺的响应曲线可以看出，轴箱加速度可以用来测量低频段也就是长波长的不平顺，因为低频段钢轨的振动比较弱，车轮基本是跟随钢轨表面的不平顺振动。频率较高的情况下，车轮的响应由于多车轮间的耦合作用呈现很大的不确定性，而且受车辆和轨道的参数如轴距、扣件阻尼的影响很大。另外，高频时由支承刚度变化带来的影响也不能忽略。考虑到目前轴箱加速度的测量主要是采用二次积分的方法，也就是认为轴箱的位移完全跟随钢轨不平顺而变化，有碴轨道的测量频率范围宜为小于30 Hz，地铁减振轨道应该小于15 Hz。假设车辆运行速度为15 m/s（10 m/s），那么对应的可测波长范围分别是大于500 mm(333 mm)和1 000 mm(667 mm)。至于测量频率的下限，由具体的传感器型号和去趋势滤波算法决定。

3.2 增大测量范围的建议

可测频率范围的大小其实由车轮响应的第一个共振峰（P2共振频率）决定，也就是车轮和轨道一起在支承弹簧上共振。减小车轮的质量，可以达到增大该共振频率的效果。当车轮的质量比较小，也就是其动柔度大，轨道的动柔度也就相对比较小，因而其振动可以忽略。

减小车轮质量可以通过两种方式实现。第一种是在正常运行的车辆后面加一节较轻的拖车，且保证与前面车厢的转向架相隔足够长以避免轨道振动波的影响。第二种方法是在车厢的中间部位吊装一个较轻的测量轮，由于车厢比较长，首尾两个转向架对中间位置轨道的影响比较小。

4 结语

(1)多车轮与轨道作用下的车轮位移响应与单车轮作用的结果在高频段有很大的差别，特别是对于地铁减振轨道。由于该轨道对高频振动波的衰减比较弱，导致振动波在不同车轮间反射叠加，有些频率处增强，有些频率处抵消，使得车轮响应呈现很大的不确定性，因而采用轴箱加速度测量短波长波磨不可行。

(2)转向架的垂向位移响应会受到俯仰运动的影响，当两轮的不平顺正好反向时，俯仰运动明显，转向架中心的位移很小，且呈现周期性波谷。转向架两端的位移响应相对平稳，但高频段仍然呈现不确定性。

(3)采用轴箱加速度测量轨道不平顺的频率范围事实上受第一个共振峰（P2共振频率）限制。采用轴箱加速度二次积分法测量钢轨不平顺时，有碴轨道的测量频率应该小于30 Hz，地铁减振轨道的测量频率应该小于15 Hz。

(4)为了增大车载轴箱加速度计的测量范围，可以考虑减小测量轮的质量，通过在末节车厢后面挂质量较轻的拖车或者在车厢中间吊装测量轮来实现。

[1]GRASSIESL.Shortwavelengthrailcorrugation:fieldtrials and measuring technology[J].Wear,1996,191(1):149-160.

[2]REAL J,SALZDOR P,MONTALBAN I,et al.Determination ofrailvertical profile through inertial methods[C]. Proceedings of the institution of Mechanical Engineers, Part F:Journal of Rapid Transit,2011,225（1）:14-23.

[3]宁静，诸昌钤，张兵.基于EMD和Cohen核的轨道不平顺信号分析方法[J].振动与冲击，2013，32(4)：31-38.

[4]曹西宁，柴晓冬，郑树彬.基于Hilbert-Huang变换的轨道车辆轴箱加速度信号分析[J].仪表技术与传感器，2015，(3)：92-95.

[5]WESTEON P F,LING C S,ROBERTS C,et al.Monitoring vertical track irregularity from in-service railway vehicles [C].Proceedingsoftheinstitutionofmechanical engineers,Part F:Journal of Rail and Rapid Transit,2007, 221(1):75-88.

[6]Lee J S,Choi S,Kim S S,et al.A mixed filtering approach for track condition monitoring using accelerometers on the axleboxandbogie[J].Instrumentationand Measurement,IEEE Transactions on,2012,61(3):749-758.

[7]TSUNASHIMA H,NAGANUMA Y,KOBAYASHI T. Track geometry estimation from car-body vibration[J]. Vehicle System Dynamics,2014,52(sup1):207-219.

[8]MOLODOVA M,LI Z,DOLLEVOET R.Axle box acceleration:Measurement and simulation for detection of short track defects[J].Wear,2011,271(1):349-356.

[9]LI Z,MOLODOVA M,NÚÑEZ A,et al.Improvements in axle box acceleration measurements for the detection of lightsquatsinrailwayinfrastructure[J].Industrial Electronics,IEEE Transactions on,2015,62(7):4385-4397.

[10]WEI X,LIU F,JIA L.Urban rail track condition monitoring based on in-service vehicle acceleration measurements[J].Measurement,2016,80:217-228.

[11]GRASSIE S L.Measurement of railhead longitudinal profiles:a comparison of different techniques[J].Wear, 1996,191(1):245-251.

[12]WU T X,THOMPSON D J.Vibration analysis of railway track with multiple wheels on the rail[J].Journal of Sound and Vibration,2001,239(1):69-97

Dynamic Response ofAxle-boxes to Rail Unevenness Excitation due to Multiple Wheel-rail Interactions and Its MeasurabilityAnalysis

FANGGe,WU Tian-xing,PENG Zhi-ke,WANG Yu-rong
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)

Track irregularities can aggravate wheel/rail interaction and thus induce fatigue and damage of wheel/rail components and noise.This is always the key point of track maintenance.Considering the economy of maintenance work, real-time monitoring of track unevenness becomes very important.The most frequently used method of track unevenness monitoring is the double integrating of the axle-box acceleration.Unfortunately,the axle-box response is found to be influenced by various factors.To obtain a better understanding of measurement results,the dynamic behavior of the axle-box response to the unevenness excitation due to multiple wheel/rail interactions is analyzed in frequency domain with the“moving irregularity”model.Based on the analysis of the axle-box response,the measurability of track unevenness is discussed.Results show that the response of the axle-box to track unevenness at low frequencies is nearly ideal,whereas at high frequencies it is influenced by the standing waves formed among the wheels and shows a variety of uncertainty due to wave reflections.Finally,some suggestions for extending the range of measurable wavelength are proposed.

vibration and wave;track irregularity;axle-box acceleration;multiple wheels interaction;standing wave

TH113.1

A

10.3969/j.issn.1006-1355.2017.02.003

1006-1355(2017)02-0013-05+100

2016-11-02

国家自然科学基金资助项目（11572188、11472170）

方格（1992－），男，湖北省黄冈市人，硕士研究生，主要研究方向为高弹性轨道波磨机理及其抑制和测量方法。Email:fang8790@sjtu.edu.cn

彭志科（1974－），男，博士生导师。E-mail:z.peng@sjtu.edu.cn