转子系统振动特性演化规律研究

花纯利，曹国华，冯世哲，刘后广

（1.上海交通大学舰船设备噪声与振动控制技术国防重点学科实验室，上海200240；2.中国矿业大学机电工程学院，江苏徐州221116）

转子系统振动特性演化规律研究

花纯利1,2，曹国华2，冯世哲2，刘后广2

（1.上海交通大学舰船设备噪声与振动控制技术国防重点学科实验室，上海200240；2.中国矿业大学机电工程学院，江苏徐州221116）

基于碰摩理论建立Jeffcott转子系统动力学模型，基于现代非线性动力学和分叉理论对转子系统进行深入分析，确定周期无碰摩响应的边界、碰摩运动的边界及其稳定性边界。对系统参数阻尼比和偏心率对转子系统振动响应特性随旋转速度演化规律的影响进行详细分析，得到不同振动响应演化方式在阻尼比和偏心率参数平面上的分布，给出各种转子系统响应特性随旋转速度的演化规律。分析结果有助于更好地理解转子系统的无碰摩周期运动、同频全周碰摩运动、局部碰摩运动、反向涡动失稳以及跳跃现象等动态响应特性和系统参数之间的关系。

振动与波；转子系统；非线性振动；稳定性；碰摩；演化规律

燃气轮机、航空发动机、舰船轴系、电动机以及提升机主轴等旋转机械被广泛地用于诸多工业生产部门中，因此旋转机械的各种异常振动可能严重威胁机械的安全运转，甚至可能导致重大的安全事故。因此，研究转子系统非线性动力学行为和系统参数之间的关系，揭示转子碰摩条件、稳定性条件以及振动特性演化规律对优化转子系统设计和故障诊断都具有十分重要的意义。

关于转子系统非线性动力学特性的研究，已有大量的研究成果。许多学者已经从实验分析、理论数值模拟分析等方面对转子系统的非线性动力学特性开展了广泛而深入的研究，并发现转子系统中可能出现的丰富动力学现象，如：跳跃现象[1–3]、同频全周碰摩运动[4]、准周期的局部碰摩[5–6]、亚谐和超谐碰摩响应以及混沌行为[7–9]。到目前为止，虽然在大量研究成果中涉及了系统参数对转子系统动态响应特性的影响，但鲜有在阻尼比和偏心率参数平面上给出转子系统响应特性演化规律的分布。文中将分析转子系统发生碰摩和鞍结分叉的边界条件，并分析转子系统的稳定性，给出转子系统不同演化方式在阻尼比和偏心率参数平面上的分布规律；并讨论系统参数阻尼比和偏心率对系统振动响应特性随旋转速度演化规律的影响，并对不同的演化规律进行讨论分析。

1 模型与运动控制方程

1.1 动力学模型的建立

转子系统模型如图1所示，质量为m的刚性转子支撑在刚度为k、阻尼为c的无质量弹性轴上，转子和定子之间的间隙为δ，转子的质心O3与其几何中心O2之间的距离为偏心距e，定子内环面的碰摩接触刚度为kr，以转子初始形心位置O1为原点建立XO1Y固定坐标系。

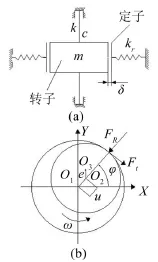
图1 转子系统模型

则转子和定子之间的摩擦力和接触力为

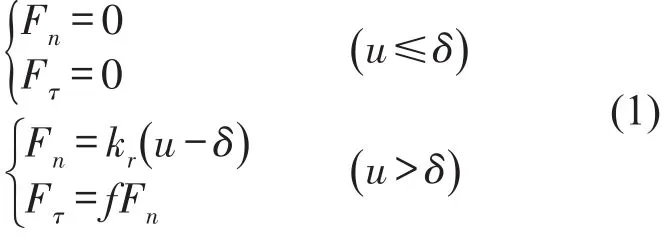
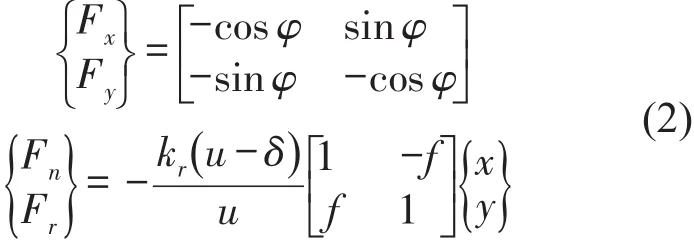
则Jeffcott转子系统动力学方程可表达为

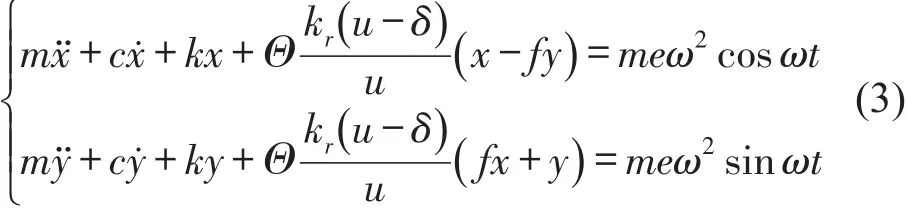
Jeffcott转子系统动力学方程可无量纲化为

1.2 无碰摩运动条件

在运转过程中，系统在转子和定子接触和不接触状态下都应有稳定的周期解。假设其解的形式为

在定子和转子没有发生接触状态下Θ=0，此时将式(5)代入控制方程式（4）并求解，可得系统响应的振动幅值和相位角分别为

由于定子和转子间的间隙是有限的，所以非接触状态下解出的振动幅值A必须满足A≤1条件。即

ρ为偏心距e与间隙δ的比值，则其值将恒大于零。

当ρ≥1时，即e≥δ，

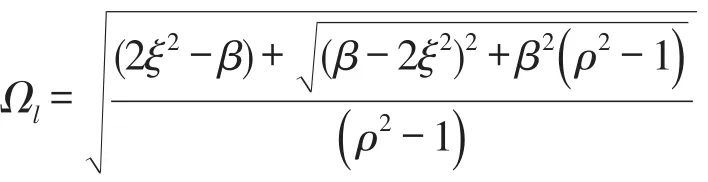
当ρ＜1时，即e＜δ，

随着旋转速度的不断增加，转子系统振动幅值A不断增大，且当旋转速度大于

1.3 碰摩运动条件

在定子和转子发生接触状态下Θ=1，将式(5)代入方程组(4)可得关于振动幅值A的方程为

其中

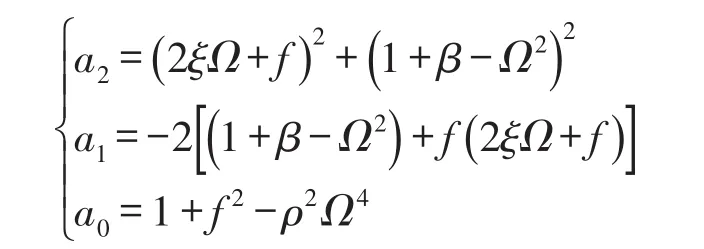
转子系统出现鞍结分岔的条件为

通过联合求解方程式(9)和式(8)划定幅值A范围，可以得到非线性方程的鞍结分岔边界。

转子系统的振动幅值A不仅是正实数，而且需满足A＞1的条件来确保定子和转子处于接触的状态，进而求得接触状态的上边界Ω=Ω1和下边界Ω=Ω2。

2 周期解的稳定性分析

式中

为简单起见，引入稳态周期解的形式如下

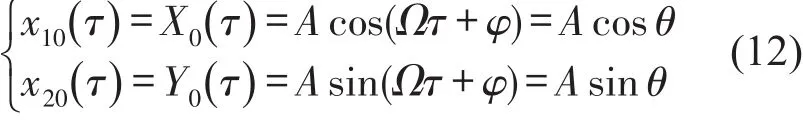
其中在接触状态和非接触状态下的振动幅值A可分别通过方程式(6)和式(8)求解。

通过在解(12)附近线性化方程(11)可得

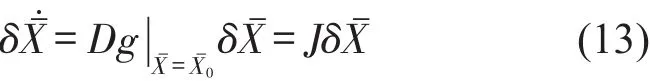
式中D为一微分算子，J为一雅可比矩阵，为稳态周期解的扰动。ˉ解的稳定性由雅可比矩阵J的特征值决定解的稳定性也反映着方程(11)解的稳定性，因此，我们只需要分析方程(13)解的稳定性就可以决定方程(10)对应解的稳定性，同时也得出了接触和非接触状态下系统方程解的稳定性。

当Θ=0时转子和定子处于非接触状态，雅可比方程J恰好是矩阵B，则其对应的特征方程为|B-λI|=0，将其展开为

根据Routh-Hurwitz（劳斯-霍尔维茨）稳定性判据，可以求得方程式(4)（Θ=0时）非接触时解的稳定性条件为

因此，当系统的阻尼是正阻尼时，非接触状态下的解是稳定的。当振动幅值大于间隙δ时，定子和转子将发生碰摩，转子系统的控制方程中的Θ=1。

当Θ=1时，控制方程式(4)的解将是非线性的周期解，其雅可比矩阵J为

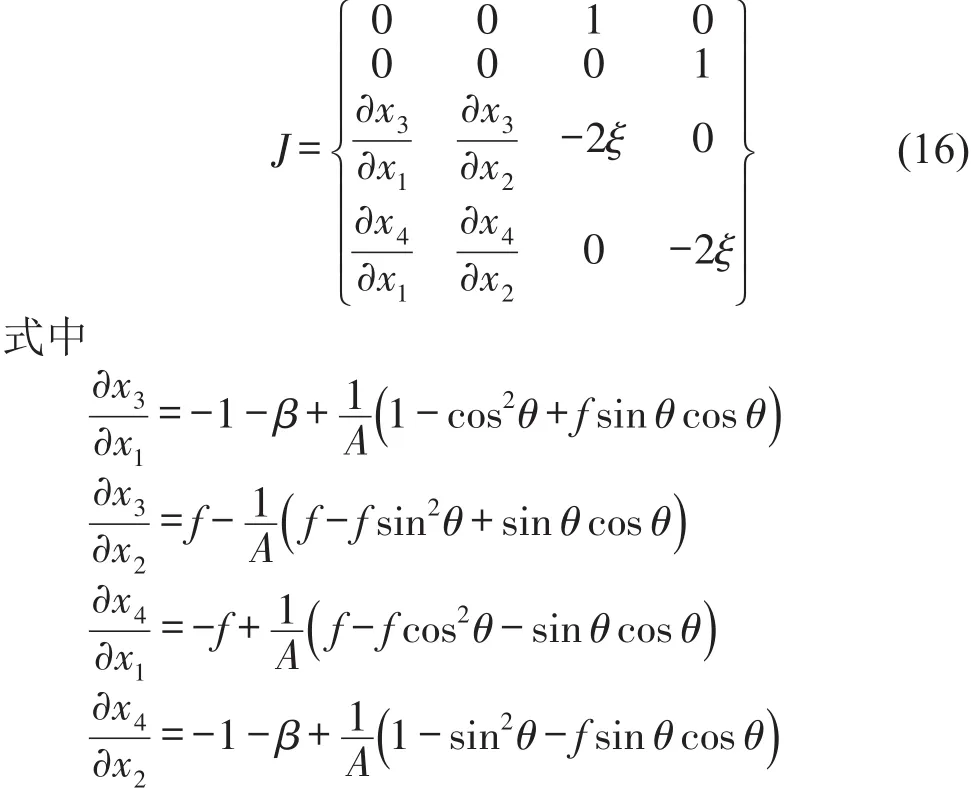
可以看出雅可比矩阵是周期性的时间依赖矩阵，所以不能直接推导和分析出其解的稳定性，因此需进行如下变换

式中转换矩阵T为

将式(17)代入方程式(13)，得

由方程式(19)可知雅可比矩阵Jc和时间参数无关。δU的解和方程式(11)解的稳定性取决于矩阵Jc特征值实部的符号。对应的特征方程满足|Jc-λI|=0，将其展开为

其中

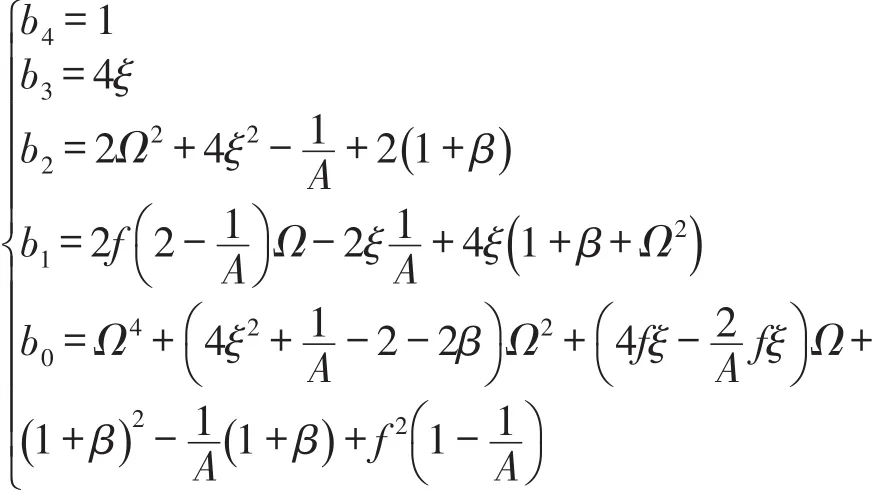
这些系数为振动幅值A的函数，所以Routh-Hurwitz（劳斯-霍尔维茨）稳定性判据可以用来判断方程式(11)接触状态时稳态周期解的稳定性。

如果雅可比矩阵Jc有一零特征值，系统将会出现鞍结分岔，此时对应方程式(20)中的b0=0。

其等效于条件(9)。通过消除幅值A的符号计算，可通过同时求解方程式(8)和式(21)而得一个关于Ω的12次多项式。经求解参数方程，可得方程式(8)发生鞍结分岔条件的参数空间。那些全周碰摩解的鞍结分岔点处的振动幅值A是大于1的正实数。

基于Hopf分叉理论，系统将会有一对共轭纯虚数特征值。将λ=±iωυ代入特征方程式(20)可得

若代入λ=-iωυ可得同样的结果。消去参数ωυ可得

其中还需满足不等式

将式(20)中的参数b0－b3代入方程式(23)并通过化简可得

式中

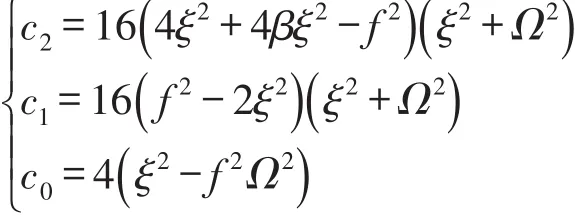
联立方程式(9)和式(25)，消去振动幅值A，经求解参数方程，可得转子系统发生Hopf分岔的参数空间。同时全周碰摩运动解的Hopf分岔点处的幅值A是大于1的正实数。

3 转子系统动力学特性分析

基于上述分析可知，转子系统的振动幅值随着系统参数的变化而不断变化，其系统响应可能会出现无碰摩、局部碰摩、同频全周碰摩和反向涡动失稳等状态。系统的响应取决于系统参数，而且不同的系统参数条件下其响应特性随转速的演化过程不同。文中主要研究阻尼比和偏心率对系统动态特性的影响，因此给定刚度β=0.5和摩擦系数f=0.2。下面将在（ρ，ξ）平面上分析系统参数偏心率和阻尼比对系统响应演化过程的影响，如图2所示。

图中的曲线将（ρ，ξ）平面分成的八个区域，分别为区域①、区域②、区域③、区域④、区域⑤、区域⑥、区域⑦和区域⑧，每一区域范围内为一种系统响应随旋转速度的演化方式。

图2 转子系统在（ρ，ξ）平面上振动响应演化规律分布图

转子系统响应随旋转速度的演化过程分别如图3－图10所示。在系统参数区域①范围内，转子系统响应的演化过程如图3所示。即转子系统的振动幅值随旋转速度的增大而不断增大，并在其固有频率处达到最大值，随着旋转速度的继续增大振动幅值逐渐减小并趋近于ρ。在该参数区域的转子系统的振动幅值始终小于转子与定子之间的间隙，即系统始终做无碰摩周期运动。

图3 转子系统振动响应演化方式一

图4 转子系统振动响应演化方式二

转子系统的参数在区域②范围内时，系统振动响应的演化规律如图4所示，即在较低转速的工况下转子系统的振动幅值小于转子和定子之间的间隙，系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而不断增大，并在Ω=Ωl时系统发生碰摩，且系统做同频全周碰摩运动，系统的振动幅值在接触状态下的固有频率处达到最大值，随旋转速度继续增大系统振动幅值不断减小，并在Ω=Ω2处转子定子脱离，做无碰摩运动，转子系统的振动幅值不断减小并趋近于ρ。

转子系统的参数在区域③范围内时，系统振动响应的演化规律如图5所示。

图5 转子系统振动响应演化方式三

在较低转速的工况下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而增大，在Ω=Ωl时系统发生碰摩，并做同频全周碰摩运动，当Ω=Ω2时转子和定子脱离并发生跳跃现象（振动幅值突变），随着旋转速度继续增大系统的振动幅值逐渐减小并趋近于ρ；若转子系统从高旋转速进行降速，转子系统的振动幅值随着旋转速度的减小而逐渐增大并在Ω=Ωu处转子定子发生接触，并发生跳跃现象，随着旋转速度继续减小，系统将在Ω=Ωl=Ω1时转子和定子脱离。

转子系统的参数在区域④范围内时，系统振动响应随旋转速度变化的演化规律如图6所示。

图6 转子系统振动响应演化方式四

在低转速下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而增大，并在Ω=Ωl时系统发生碰摩，做同频全周碰摩运动，随着旋转速度继续增大振动幅值不断增大，并在某转速后同频全周碰摩运动失稳，系统响应转变为局部碰摩运动，旋转速度继续增大，系统将在某转速后出现反向涡动失稳（图中的空白区域）。若转子系统从高旋转速度进行降速，系统振动幅值随着旋转速度的减小而逐渐增大，并在Ω=Ωl时转子定子接触并发生反向涡动失稳。

转子系统的系统参数在区域⑤范围内时，系统振动响应随旋转速度变化的演化形式如图7所示。

图7 转子系统振动响应演化方式五

在低转速下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而增大，并在Ω=Ωl时系统发生碰摩，此时系统做局部碰摩运动，随着旋转速度继续增大系统将在某转速后发生反向涡动失稳。若转子系统从高旋转速度进行降速，系统振动幅值随着旋转速度的减小而逐渐增大，并在Ω=Ωl时转子定子接触并发生反向涡动失稳。

若系统参数在区域⑥范围内，转子系统振动响应的演化规律将如图8所示。

图8 转子系统振动响应演化方式六

在较低转速的工况下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而不断增大，并在Ω=Ωl时系统发生碰摩并做同频全周碰摩运动，系统的振动幅值在接触状态下的固有频率处达到最大值。旋转速度继续增大，转子系统的响应一直处于同频全周碰摩状态，且其振动幅值不断减小并趋近于ρ。

若系统参数在区域⑦范围内，转子系统振动响应的演化规律将如图9所示。

在较低转速的工况下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而不断增大，并在Ω=Ωl时系统发生碰摩，并做同频全周碰摩运动。随着旋转速度继续增大振动幅值不断增大，并在某转速后同频全周碰摩运动失稳，系统响应转变为局部碰摩运动，旋转速度继续增大系统将在某转速后出现反向涡动失稳。在任何初始条件下，高旋转速度下的转子系统均处于反向涡动失稳状态。

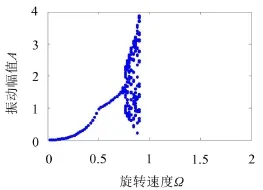
图9 转子系统振动响应演化方式七

转子系统的参数在区域⑧范围内时，系统振动响应的演化规律将如图10所示。

图10 转子系统振动响应演化方式八

在较低转速的工况下转子系统做无碰摩周期运动，系统振动幅值随着旋转速度的增大而不断增大，并在Ω=Ωl时系统发生碰摩，此时系统做局部碰摩运动，随着旋转速度继续增大系统将在某转速后发生反向涡动失稳。在任何初始条件下，高旋转速度下的转子系统均处于反向涡动失稳状态。

4 结语

以Jeffcott转子系统为研究对象，对转子系统发生碰摩条件进行讨论，对系统发生同频全周碰摩运动的参数条件及其稳定性进行深入研究。分析阻尼比和偏心率对转子系统振动响应特性随旋转速度的演化规律的影响。基于此可以得出如下结论：

(1)在较低转速状态下，转子系统均做无碰摩周期运动；当旋转速度较高且偏心率ρ≥1时，任何初始条件下转子系统都将做碰摩运动；当偏心率ρ＜1时，在较高转速条件下转子系统既可能做无碰摩周期运动也可能做同频全周碰摩运动、局部碰摩运动或是反向涡动失稳。

(2)阻尼比和偏心率参数平面被曲线分为八个区域，在每个参数区域内转子系统的响应均有一种演化方式。在阻尼比足够小且偏心率足够大的条件下转子系统才会出现碰摩现象。且系统阻尼比越大、偏心率越小转子系统就越稳定。跳跃现象只在一定阻尼比和偏心率范围内才有可能发生，阻尼比太大或太小、偏心率过大或过小均不可能出现跳跃现象。

[1]JIANG JUN,ULBRICH H.Stability analysis of sliding whirl in a nonlinear jeffcott rotor with cross-coupling stiffness coefficients[J].Nonlinear Dynamics,2001,24: 269-283.

[2]SHANG ZHIYONG,JIANG JUN,HONG LING.The global responses characteristics of a rotor/stator rubbing system with dry friction effects[J].Journal of Sound and Vibration,2011,330:2150-2160.

[3]HUA CHUN-LI,TA NA,RAO ZHU-SHI.Dynamic characteristics analysis of a rub-impact rubber bearingshaft system[J].Journal of Vibration and Control,2015, 21(2):388-401.

[4]花纯利，塔娜，饶柱石.橡胶轴承-转轴系统碰摩响应动力学特性研究[J].振动与冲击，2014，33(2)：26-30.

[5]HUA CHUN-LI,RAO ZHU-SHI,TA NA,et al.Nonlinear dynamics of a rub-impact rubber bearing-rotor system with Stribeck friction model[J].Journal of Mechanical Science and Technology,2015,29(8):3109-3119.

[6]KIM Y B,NOAH S T.Quasi-periodic response and stability analysis for a nonlinear Jeffcott rotor[J].Journal of Sound and Vibration,1996,190:239-253.

[7]GOLDMAN P,MUSZYNSKA A.Chaotic behavior of rotor/stator system with rubs[J].Journal of Engineering for Gas Turbines and Power,1994,116:693-701.

[8]EVGUENI V K,WIERCIGROCH M,CARTMELL M P. Regularandchaoticdynamicsofadiscontinuously nonlinear rotor system[J].Chaos,Solitons and Fractals, 2002,13:1231-1242.

[9]褚福磊，张正松，冯冠平.碰摩转子系统的混沌特性[J].清华大学学报(自然科学版)，1996，36（7）：52-57.

Study on the Evolution Law of the Dynamics Characteristics of Rotor Systems

HUA Chun-li1,2,CAO Guo-hua2,FENG Shi-zhe2,LIU Hou-guang2
(1.Defense Key Disciplines Laboratory of Ship Equipment Noise and Vibration Control Technology,Shanghai Jiaotong University,Shanghai 200240,China; 2.School of Mechatronic Engineering,China University of Mining and Technology, Xuzhou 221116,Jiangsu China)

The dynamic model of a Jeffcott rotor system is established based on the impact theory and analyzed by the modern nonlinear dynamics and bifurcation theories.The no rub-impact,the rub-impact boundary and the stable boundary are determined.The influence of the system parameters such as damping radio and eccentricity on the evolution law of the dynamics characteristics of the rotor system is studied.Several kinds of evolution are then obtained in the parameter spaces of the damping radio and eccentricity,and the evolution law of the dynamics characteristics of the rotor system with the changing of rotational speeds is given.These results provide an opportunity for a better understanding of the relationship between the system parameters and the dynamical characteristics,such as periodtc no-rub motion,the synchronous full annular rub motion,partial rub motion,the dry whip as well as the jump phenomena.

vibration and wave;rotor system;nonlinear vibration;stability;rub-impact;evolution law

O322

A

10.3969/j.issn.1006-1355.2017.02.001

1006-1355(2017)02-0001-06+61

2016-11-04

国家自然科学基金资助项目（51505476）；上海交通大学舰船设备噪声与振动控制技术国防重点学科实验室开放基金资助项目（vsn201601）

花纯利（1983－），男，江苏省徐州市人，讲师，主要研究方向为转子动力学、结构动力学。E-mail:huachunli@163.com