液压挖掘机动力系统振动分析与控制

俞松松，张影，刘兴鑫

(广西柳工机械股份有限公司，广西柳州545007)

液压挖掘机动力系统振动分析与控制

俞松松，张影，刘兴鑫

(广西柳工机械股份有限公司，广西柳州545007)

针对某挖掘机主泵剧烈振动问题，应用拉格朗日方程建立动力系统的动力学模型，得到动力系统的刚体模态频率，通过分析排除刚体模态共振的可能。利用有限元方法，对比分析法兰厚度、主泵重心至法兰距离对动力系统结构模态频率的影响，对关键参数进行识别和优化。对优化前后主泵振动进行对比测试，发现振动有效值降幅达75.7%，验证了理论建模、分析及测试方法的正确性。

振动与波；动力系统；共振；模态分析；固有频率；法兰

挖掘机作为工程机械之王，在采石、铁路、建筑及市政等领域发挥着越来越大的作用。近年来，工程机械领域对挖掘机的可靠性与寿命提出了更苛刻的要求，对舒适性与操作性的要求也在不断提高[1]。而挖掘机动力系统的设计优良程度直接影响整机及零部件的寿命。因此，动力系统减震器的刚度、位置及角度等参数应进行合理设计，保证动力系统的刚体模态频率在发动机工作频率之外，以避免系统共振[2]。以此同时，也应保证其附属部件（如安装支架、连接装置等）的结构模态频率在发动机工作频率范围内，以避免局部共振。动力系统的模态计算、减震器的参数设计与优化等方法，在汽车行业已较成熟，在此不作累述[3–4]。而在工程机械行业，国内开展NVH（Noise Vibration Harshness）研究起步较晚，由于技术水平与工程经验的欠缺，导致出现的NVH故障，因缺少相应的测试、诊断手段与规范，无法有效地得到解决与控制。

针对挖掘机的主泵振动剧烈问题，对动力系统进行理论建模，结合仿真技术，分析并识别共振源头与关键参数，对比分析结构参数对动力系统结构模态频率的影响。对结构参数进行优化，并对优化前、后主泵振动进行了对比测试，发现振动RMS值降幅达75.7%。该减振分析与改进的方法可为工程应用提供理论与试验依据。

1 动力学模型

挖掘机的动力系统主要由风扇、发动机及减震器支座、消声器及支架、法兰及主泵等几大部件组成。为了稳定性及制造方便，一般采用四个减震器平置安装方式，动力系统的动力学模型如图1所示。

挖掘机动力系统的减震器一般采用橡胶元件，由于其阻尼不大，且对刚体模态频率无影响。应用拉格朗日方程，动力系统的自由振动方程可表示为

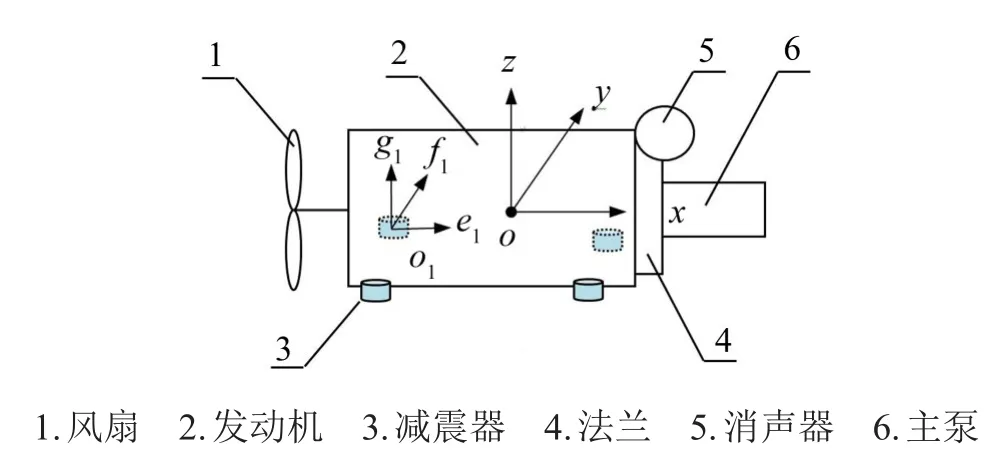
图1 动力系统的动力学模型

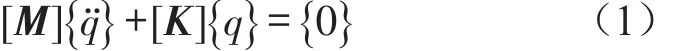
式中M为系统质量矩阵；K为系统刚度矩阵；q为广义坐标；

由机械振动知识可知，M-1K的特征值和特征向量分别为动力系统的固有频率和固有振型。

其中M、K分别如式（2）、式（3）所示。

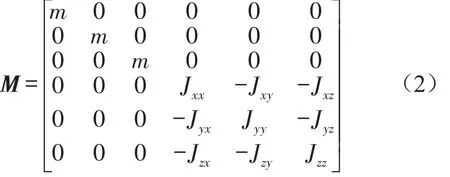
式中m为发动机动力总成的质量；Jxx、Jyy、Jzz分别为动力系统绕x、y、z轴的转动惯量；Jxy、Jyz、Jxz分别为动力系统绕x、y、z轴的惯性积。

式中Ai为第i个减震器的局部坐标系Oieifigi与坐标系Oxyz的转换矩阵；Bi为第i个减震器相对于坐标系Oxyz的方向余弦矩阵；Ki为第i个减震器的刚度矩阵；式（3）中

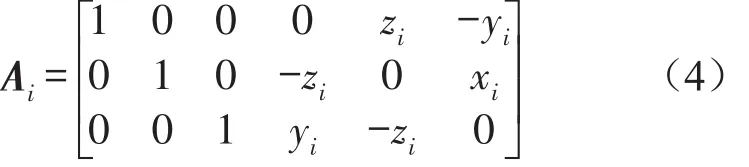
式中xi、yi、zi为第i个减震器在坐标系Oxyz下的坐标

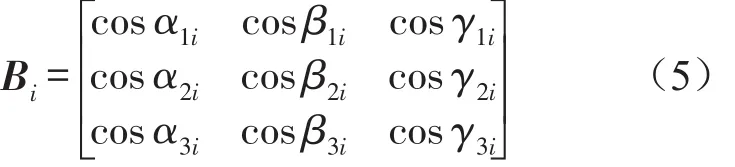
式中α1i、β1i、γ1i为第i个减震器的e轴相对于x、y、z轴的交角；α2i、β2i、γ2i为第i个减震器的f轴相对于x、y、z轴的交角；

α3i、β3i、γ3i为第i个减震器的g轴相对于x、y、z轴的交角；

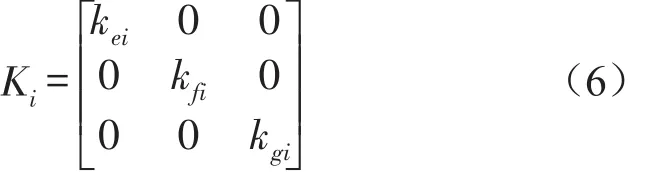
式中kei、kfi、kgi为第i个减震器沿ei、fi、gi向的动刚度；

2 故障诊断

2.1 振动测试

该挖掘机搭载直列4缸4冲程发动机，通过对液压主泵进行振动测试，三向加速度传感器布置在主泵侧面（见图2）。

图2 主泵振动测试

测试发现随着发动机转速增大，主泵表面的振动越大，液压管路振动越剧烈，导致液压管路的可靠性及寿命大大降低。原机主泵z向振动瀑布图如图3所示。

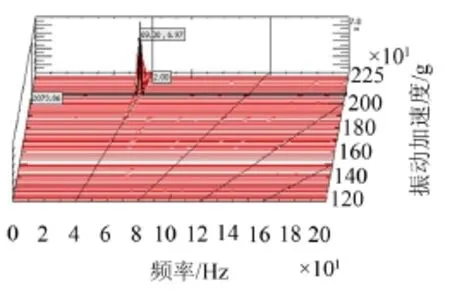
图3 原机主泵z向振动瀑布图

可知主泵z向振动先变大再变小，并在69 Hz时达到最大值，说明在z向上可能存在频率耦合，引发了共振现象，一是动力系统的刚体模态频率与发动机工作频率耦合，二是部件的局部模态频率与发动机工作频率耦合。

2.2 理论计算与分析

直列4缸4冲程发动机的主要激励为曲柄连杆机构不平衡的往复运动质量所产生的惯性力及惯性力矩[5]，可由式（7）计算得到

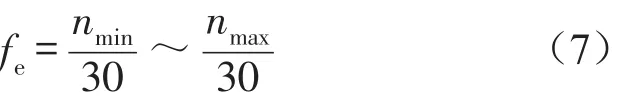
式中fe为发动机的工作频率范围；nmin为发动机的怠速转速，nmax为发动机的最高转速。

动力系统的相关参数如表1所示。

由于动力系统关于x轴对称，则主泵端两个减震器选用同一型号，风扇端的两个减震器选用另一型号。将参数代入式（1）－式（7），可得动力系统的各阶刚体模态频率，如表2所示。

根据式（7），发动机的工作频率范围为36.7 Hz～80 Hz，由隔振理论可知，当频率比λ≥1.41，即动力系统的刚体模态频率小于fe/λ时，才能起到隔振作用，但在工程应用上，考虑履带式挖掘机行走时，路面给予的激励频率在10 Hz左右，动力系统的刚体模态频率不能太低，故频率比λ一般取1.2以上[6]，那么，须将动力系统的第6阶固有频率控制在30.58 Hz以内。

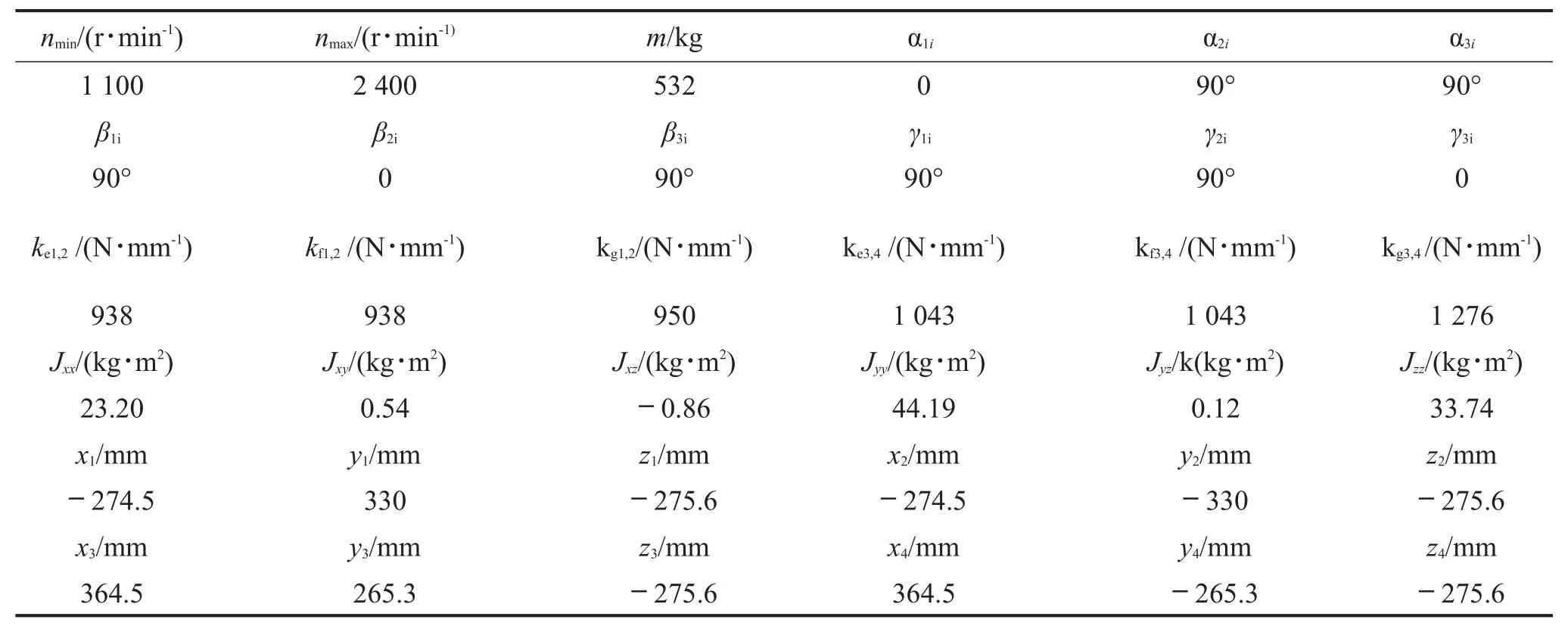
表1 动力系统的相关参数

表2 动力系统的各阶刚体模态频率

表2中的f11～f16分别为动力系统第1阶～6阶刚体模态频率，可知最高阶（第6阶）固有频率为29.36 Hz，小于上述分析的30.58 Hz，可避免动力系统的模态频率与发动机工作频率耦合，故满足隔振要求。

3 优化设计与验证

3.1 有限元分析

上述分析排除了动力系统刚体模态共振的可能性，为了识别共振源头，进一步对动力系统进行结构模态分析。由于风扇、消声器等对主泵的振动影响不大，故不作考虑，简化的实体模型如图4所示。

由于缺失发动机及主泵，分析时根据发动机轮廓将三维实体模型进行相应简化，并保证其质量中心与中心位置一致。主泵视为质量点（140 kg），位置设置在相应的重心处[7]。完全约束四个支座安装孔的6个自由度，由于模型最小板厚为12 mm，故用实体单元进行网格划分，保证板厚具有3层及以上网格，单位总数为215 152个，建立如图5所示的有限元模型。

分析得图6所示的动力系统前4阶模态振型（模态频率见表3）。

图4 动力系统的实体模型

图5 动力系统的有限元模型

表3 动力系统的各阶结构模态频率

由图可知，动力系统的前3阶模态振型主要以法兰局部模态变形为主，支座模态变形较小，因设计时支座的第1阶固有频率要求在600 Hz以上，故在第4阶振型中支座才开始出现明显模态变形，进一步说明整个动力系统中，法兰的刚性最弱，且模态频率在发动机的工作频率范围之内，存在共振的可能。结合表3的第1阶模态频率f21与模态振型发现，其与图3所实测的共振频率69 Hz非常吻合，且振动方向也保持一致，验证了故障由法兰的局部振动导致的结论。

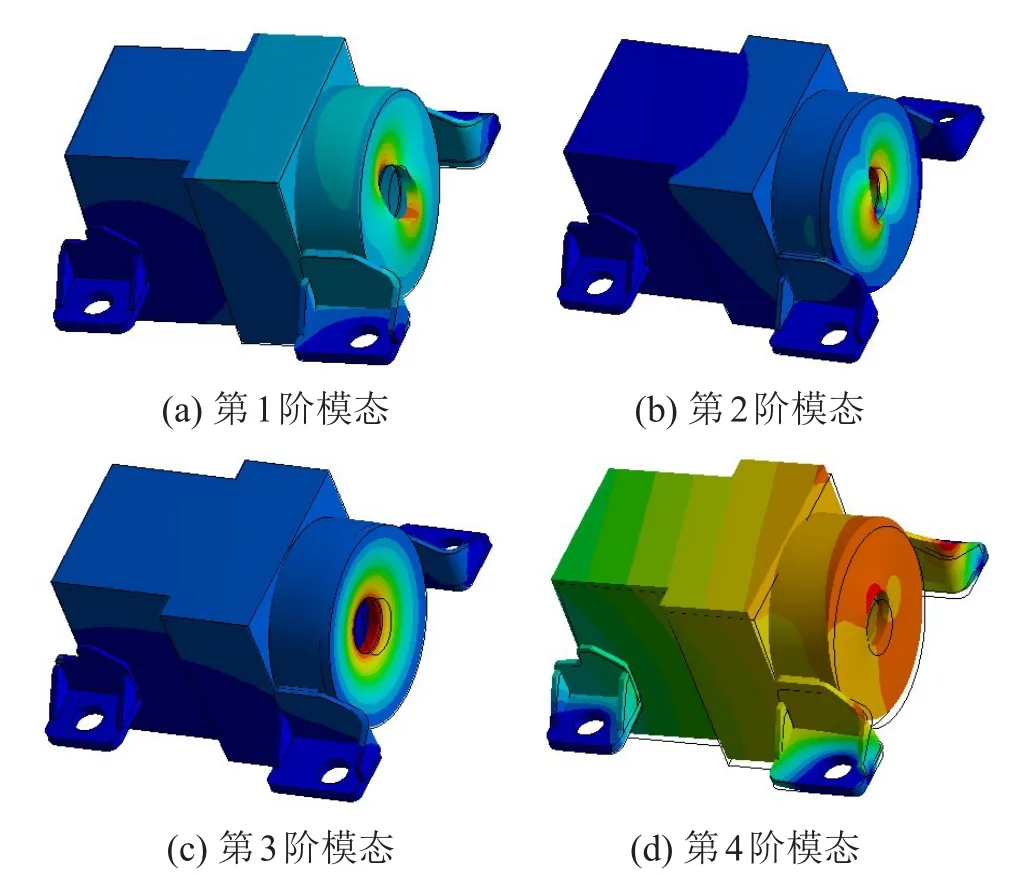
图6 动力系统的前4阶模态振型

3.2 参数优化与测试

为了有效提高动力系统的第1阶模态频率，首先应分析影响其第1阶模态频率的关键参数。由结构力学知识可知，关键参数为主泵重心至法兰端面的距离l、法兰绕y向的局部摆动刚度kθy，欲增大f21，应尽量增大kθy值并减小l值。增大kθy通常有加筋及增加法兰厚度t两种方法，由于原12 mm厚的法兰已有加强筋，故只分析厚度t对f21的影响，t值分别取12 mm、15 mm、18 mm及21 mm，得f21随法兰厚度t的变化关系，如图7所示。

图7 f21随法兰厚度t的变化关系

同理，l值分别取200 mm、210 mm、220 mm、原机值230 mm、240 mm及250 mm，得图8所示f21随l变化关系。

观察图7和图8可知，f21随厚度t的增大而增大，成类似正比的线性关系，f21随距离l的增大而线性减小，且厚度t对f21的影响较距离l大，因此增加厚度t是提高f21最直接有效的措施。当t=21 mm，l=230mm时，f21=96.48 Hz，大于发动机最高工作频率80 Hz的1.2倍，满足隔振要求。

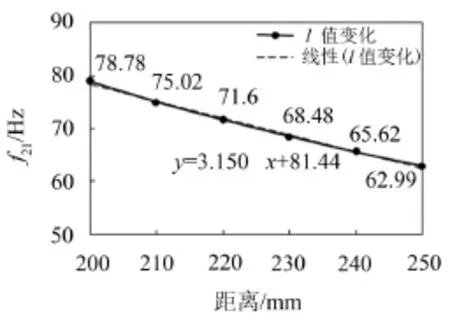
图8f21随l的变化关系

图9为加厚法兰后（t=21 mm），采用相同测试方法（见图2），主泵z向的振动测试瀑布图，可知在69 Hz附近主泵z向的共振现象完全消失（对比图3）。图10为改进前、后主泵z向振动RMS值随发动机转速的变化，可知振动由2.88 g减小为0.7 g，降幅达75.7%。

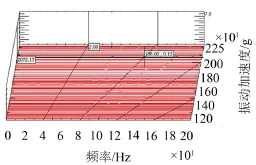
图9 改进后主泵z向振动瀑布图

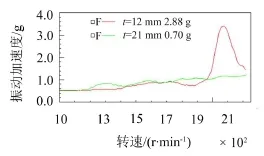
图10 主泵z向振动随发动机转速变化对比

4 结语

（1）应综合考虑由于减震器刚度匹配不合理导致的刚体模态问题及结构设计不合理导致的局部模态问题，为工程机械的动力系统设计及故障排除提供参考意见。

（2）结构设计时，应充分分析相关参数对结构模态的影响，识别出关键参数，避免出现共振现象。

（3）主泵改进前后的振动测试结果对比证明所作改进有效地控制了主泵的振动，其降幅为75.7%，验证了测试与对比分析方法的正确性。

[1]刘丕晶，侯亮，黄伟，等.挖掘装载机动力总成悬置系统隔振性能仿真[J].厦门大学学报（自然科学版），2012，51 (6)：1005-1009.

[2]张义民.机械振动[M].北京：清华大学出版社，2007.

[3]杨雷，黄鼎友，王鑫峰，等.Matlab在动力总成悬置系统优化设计的应用[J].机械设计与制造，2011(5)：93-95.

[4]张德满，李舜酩，尚伟燕，等.发动机悬置系统参数的优化设计[J].机械设计，2003，20(3)：53-55.

[5]庞剑，谌刚，何华，等.汽车噪声与振动-理论与应用[M]. 2006.

[6]黄鼎友，许荣明.基于Matlab的发动机悬置系统设计及优化[J].噪声与振动控制，2007，27(1)：57-60.

[7]周昌水.汽车发动机悬置优化技术研究[D].重庆：重庆大学，2006.

VibrationAnalysis and Control of the Hydraulic Excavator’s Power System

YU Song-song,ZHANGYing,LIU Xing-xin
(Guangxi Liugong Machinery Co.Ltd.,Liuzhou 545007,Guangxi China)

In view of the acute vibration of the excavator’s pump,the dynamic model of the power system of the excavator is established using Lagrange equation.The rigid modal frequency of the power system is obtained.The resonance possibility resulted from the rigid modal frequency is obviated.Based on finite element method,the influence of the flange thickness and the distance from the mass center of the pump to the flange on the structural modal frequency is analyzed.The key parameters are recognized and optimized.The vibration of the pump is tested before and after the optimization and the results are compared.It is found that the vibration RMS of the pump is reduced by 65.6%,which verifies the correctness of the modeling,analysis and test.

vibration and wave;power system;resonance;modal analysis;natural frequency;flange

TH122

A

10.3969/j.issn.1006-1355.2017.02.041

1006-1355(2017)02-0203-04+220

2016-09-05

国家863计划资助项目（2014AA041502）

俞松松(1987－)，男，南昌市人，硕士，主要研究方向为挖掘机的振动与噪声控制、振动舒适性分析。E-mail:yuss0417@163.com