压电悬臂梁机电耦合系统的建模及动力学特性分析

张梦倩，宋汉文

(同济大学航空航天与力学学院，上海200092)

压电悬臂梁机电耦合系统的建模及动力学特性分析

张梦倩，宋汉文

(同济大学航空航天与力学学院，上海200092)

基于压电能量采集器中最为经典的压电悬臂梁模型展开研究。考虑悬臂梁的阵型信息和轴向应变分布，这导致与梁耦合的压电片的电边界条件复杂。分别基于均匀电场分布和均匀电位移分布的两种不同电边界条件，深入探讨压电悬臂梁的机电耦合原理和耦合特性，并建立机电耦合系统的数学模型；在传统一阶能量采集电路的基础上，在电路中加入电感，建立二阶电路，并改进数学模型；对于加入电感后的模型，2阶电路可以与其耦合的n自由度机械系统共同构成一个n+1自由度系统，从而可对耦合系统进行系统整体的仿真分析，同时深入研究不同电路元件对系统采集效率的影响，发现电感的加入可极大提高系统能量采集效率。

振动与波；压电悬臂梁；机电耦合模型；系统仿真；功率优化

随着微电子（MEMS）技术的飞速发展，新型微能量采集器得到高度重视。压电振动能量采集器具有结构简单、能量转换密度大、易于微型化、集成化的优点，具有最为广阔的研究前景。目前，基于压电材料振动能量采集装置的研究不断深入，研究范围也不断扩大。研究领域涉及压电材料的研究、采集器结构优化、能量采集电路优化以及压电能量采集系统数学模型的构建和能量输出的预测等。

经典的压电能量采集装置为压电单晶片或压电双晶片构成的悬臂梁结构。然而微型化的压电悬臂梁结构只能实现一定频率下的振动能量收集，且固有频率高，有效采集带宽窄，难以在振动源多变的振动环境中保持较高发电效率。故而，为提高发电效率，对采集器结构提出了多种优化方法，包括在悬臂梁结构末端增加质量块，降低结构的固有频率[1]；将多个固有频率相近的单悬臂梁进行组合，设计一种悬臂梁阵列式结构[2,6]；Erturk提出一种L型多悬臂梁多质量块结构，极大地缩小了第1阶、第2阶固有频率之间的差距，在12阶固有频率之间实现内共振，提高采集带宽[3]。

其次，数学模型的有效建立亦是准确预测系统能量输出效率的关键。基于典型的压电悬臂梁结构和经典采集电路的机电耦合模型，其数学模型主要有：单自由度模型[1]、分布参数模型[4]、近似分布参数模型[5]和等效电路模型[14]等。其模型电学部分均简化为只含负载的简单电路，且假设沿悬臂梁纵向，压电片上下表面间电场强度不变，建立以悬臂梁的位移x(t)和输出电压V(t)为基本变量的机电耦合模型。此时，耦合系统的数学模型可以表示为振动的2阶微分方程和R-C电路的1阶微分方程的耦合方程组。

在采集电路中加入电感，并以悬臂梁的位移x(t)和输出电荷q(t)为基本变量，建立数学模型。假设压电片表面电位移沿着悬臂梁纵向均匀分布，在该假设下，可将n自由度的机械系统的机电耦合模型简化成n+1自由度的系统整体进行仿真分析。文中进一步研究了电感的加入对系统能量采集效率的影响，并发现，电路固有频率对外激励的频率变化更为敏感，且电路固有频率与悬臂梁一阶固有频率接近时，会大幅提高能量采集效率。

1 压电悬臂梁数学建模

选择经典的悬臂梁结构和电感电阻串联的简化电路构成的能量采集系统进行数学建模和动力学特性分析，如图1所示。

图1 压电悬臂梁式压电振动能量采集器模型示意图

采集器由金属基板、压电晶片、基座和采集电路组成，其中压电晶片作为机电转换的重要媒介，选择介电系数较高、性能更为稳定的PZT型压电陶瓷。压电片PZT层通过环氧树脂粘结到基板的上表面，沿厚度方向极化，并通过电极与外部采集电路相连。由于压电材料的各种常数取决于电场、位移、应力和应变的方向，各个参数加双下标表示其作用方向，其中应变系数d表示压电片应变和电场强度之间关系。在文中所研究的结构中，压电片表面的应变与其厚度方向的电场方向垂直，因此应变常数d31则表示1方向的应变和与其垂直的3方向电场之间的关系，因此称之为压电悬臂梁d31模型。金属基板的一端固定在基座上，另一端自由。参数l、b、hs、hp分别表示压电悬臂梁的长、宽、金属基板的厚度以及PZT的厚度。由于压电陶瓷上下表面电极的厚度很小，这里可以忽略不计。R、L分别表示外接采集电路的阻抗和电感系数。等效电容两端电压等于电阻电感两端电压总和。以悬臂梁的位移x(t)和输出电荷q(t)为基本变量，分别在均与电场和均匀电位移两种假设下建立数学模型。

1.1 均匀电场假设下耦合系统建模

建立2阶电路，简化电路图如图2所示。为了方便电路元件和力学系统参数的对应，选择悬臂梁位移wrel(x,t)和电路的总电荷量q(t)为基本变量进行数学建模。

图2 电路模型简化

对于该压电耦合模型，假设：

(1)简化电路只含有串联的电感和电阻，并与压电片与电极形成的等效电容并联；

(2)假设外界能量可以保证悬臂梁基座持续振动，以保证采集电路电能不间断；

(3)压电片在悬臂梁表面全覆盖均匀分布，且电极与外部的收集电路相连，导电性良好，电场沿压电片表面均匀分布。

选取压电片的第一类本构方程为

悬臂梁的横截面如图1（b）所示，由此可知内力矩的表达式为

将内力矩表达式代入基础位移激励下悬臂梁振动的偏微分方程，可得

再来看电路方程。电路中的电荷量可以由压电片电位移的积分获得，于是有

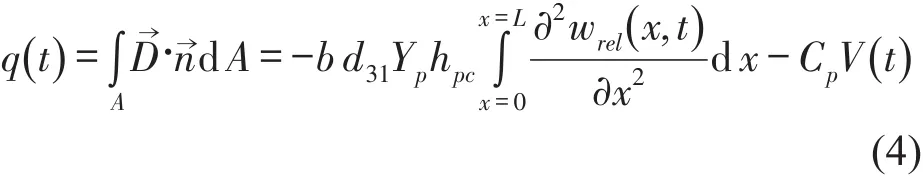
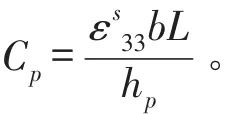
由电荷表达式和电路图(见图2)，可得关于电路电压的等式

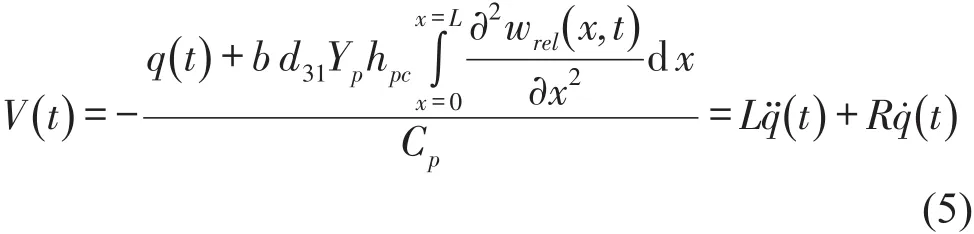
整理可得以总电荷量q(t)为基本变量的电路方程为

将悬臂梁振动微分方程中的V(t)用变量q(t)代替，得到与2阶电路耦合的压电耦合系统的数学模型

容易看出，电路电感与力学系统的质量对应，阻抗与阻尼对应，电感与刚度对应。若截取第1阶模态，将悬臂梁简化成单自由度系统[1]，则该力电耦合系统可写成方程组

可以看出，该压电耦合系统的数学模型，不同于我们常见的力学系统，其广义质量阵和广义刚度矩阵都不对称。

1.2 均匀电位移假设下耦合系统建模

再来看另一种建模方式。假设压电片上的电位移沿压电片均匀分布，此时，电位移D(t)只是关于时间t的函数，而电场分布E(x,t)则是关于x、t的函数。

取压电片的本构方程[7]

通过悬臂梁横截面，可积分得到悬臂梁的内力矩

其中

对于电路部分，假设电边界条件是电位移均匀分布，于是

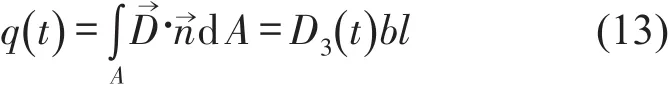
由于电场沿悬臂梁不均匀分布，故电压分布也不均匀，故等效电容两端电压取均值。由压电本构方程和电路方程，可得等式

整理可得均匀电位移假设下压电耦合系统的数学模型

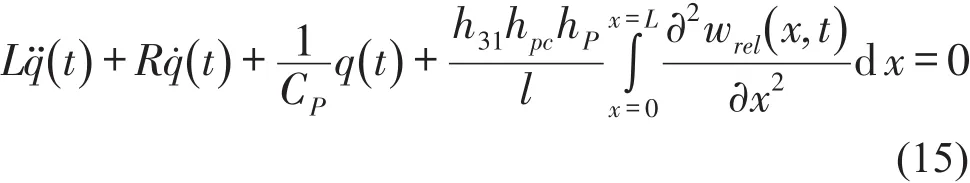
则式（11）、式（14）构成该假设下悬臂梁机电耦合系统的数学模型；将悬臂梁简化成集中参数的单自由度模型，数学模型如式（16）所示

在该假设下，压电耦合系统数学模型的广义质量阵和广义刚度阵均为对称矩阵，便于下一步的研究计算。并且容易看出，以x(t)和q(t)为基本变量建立数学模型，可以更好地描述机电耦合系统中机械和电路之间的关系。电路电感与质量对应，表示系统动能，阻尼和电阻均是耗能项，而刚度和电容均为势能项。

2 系统仿真及模型验证

表1中给出了依据文献[1]设定的压电振动能量采集器的材料和结构参数。

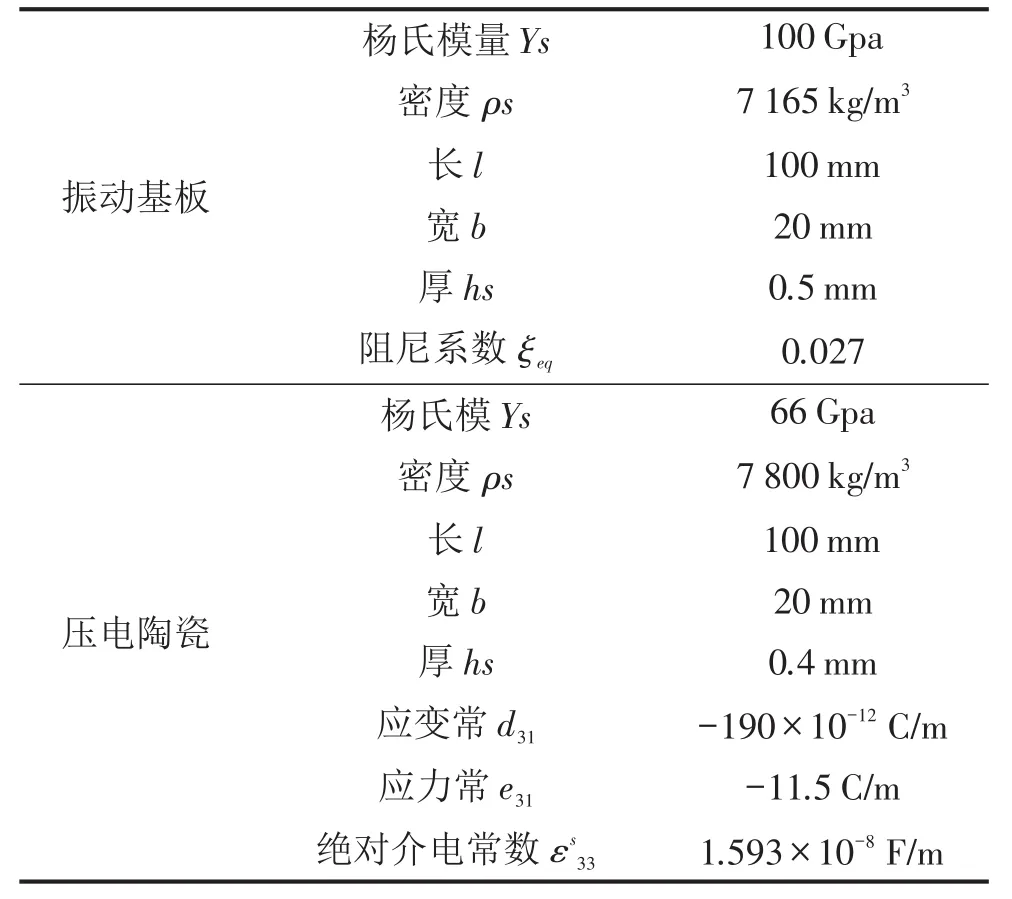
表1 压电振动能量采集器的材料和结构参数

给定2阶电路电阻为1 000 Ω、电感为500 H，则电路固有频率为25 Hz，悬臂梁系统的1阶固有频率为48 Hz；因此，简化的集总参数模型输出电压的频响函数应有25 Hz、48 Hz两个峰值；分布参数模型截取梁的前3阶，两种模型仿真对比如图3所示。

从电压响应的频谱我们容易看出，当外激励频率远远低于悬臂梁的第2阶固有频率时，可以用简化的单自由度系统来近似模拟压电悬臂梁。

接下来，采用单自由度模型进行仿真，验证两种电边界条件下系统的理论频响函数。这里，我们将单自由度力学模型和2阶电路看作一个二自由度的系统，定义力学模型的质量、刚度、阻尼为该系统的第一自由度，电路的电感、电阻、电容为系统的第二自由度，两自由度之间的耦合由机电耦合系数实现。

如图4所示，实线表示均匀电位移假设下的系统频响函数，虚线表示均匀电场假设下系统频响函数。容易看出，均匀电场假设下，系统频响函数H12和H21不对称；除了H12，两种电边界条件假设下，系统理论频响函数估计结果一致。即在弱耦合的条件下，在力学系统上施加外力激励，两种电边界条件对系统位移响应和电压响应估计结果一致；但若是在2阶电路上施加电压激励，电边界条件的不同假设则会导致响应估计产生较大误差。

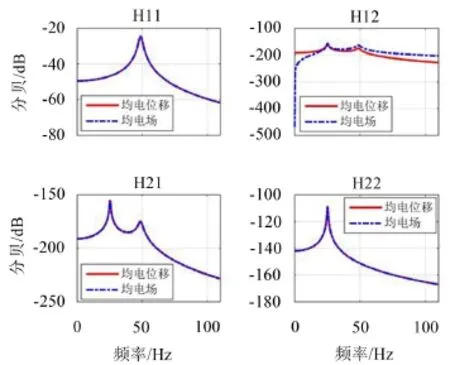
图4 两种边界条件假设下频响函数比较

在文中所述的能量采集系统中，电边界条件假设不同对系统响应估计几乎没有影响。由于，均匀电位移假设下，系统的广义质量阵和刚度阵均为对称矩阵，方便进一步的系统仿真和证明，因此，接下来的研究将采用均匀电位移假设。

3 电路参数对采集性能的影响

3.1 电阻对系统采集效率的影响

在该系统中，电阻是耗能元件，以系统的总输出电压（加载在压电片两端的电压）和电阻能耗作为判断系统输出效率的标准。

分别对200 Ω、1 000 Ω、5 000 Ω、10 000 Ω和50 000 Ω的阻抗进行系统仿真，系统输出电压及电阻耗能功率分别如图5图、图6所示。

图5 不同阻值下系统的输出电压

图6 不同阻值下耗能电阻的能力损耗功率

在电路固有频率处，阻尼越小，系统输出电压响应反而越大，而电阻能耗并没有明显变化，说明此时，电感对系统输出电压的大幅提高有显著影响；而在机械系统固有频率处，系统输出电压并不随电阻的改变而有明显变化，而随着阻尼的增大，电阻耗能增加，电阻承担更多电压，相应，电感上的电压减少。因此，在阻尼较小时，电感的存在会承担更多电压，将系统的输出电压稳定在一个较高水平。

3.2 电感对系统采集效率的影响

电感的加入，本质上改变了采集电路的性质，可以通过调节电感参数来控制采集电路的固有频率。首先比较电感的加入对系统输出效率的影响。图7分别表示同阻值下，12阶电路输出电压。

容易看出，电感的加入，将系统输出电压稳定在一个较高水平，尤其在电阻阻值较小时，使系统输出电压的提高更为显著；而当系统阻值大于2阶电路临界振荡的阻值时，电感对系统的影响不再明显，12阶电路下系统的输出电压差距不大。

再来看2阶电路系统输出响应的特征。当电路固有频率为25 Hz、机械系统固有频率为48 Hz时，系统在不同频率激励下的电压响应和位移响应（简化的单自由度系统的位移，即悬臂梁的末端位移）特征如图8所示。

图7 不同阻值工况下12阶电路输出电压比较

图8 电路固有频率为25 Hz时系统响应

容易看到，系统输出电压受机械系统的影响较大，当外激励频率在机械系统固有频率附近时，电压响应表现出明显峰值；而由于耦合极弱，机械系统受电路的影响极小，当外激励在电路固有频率附近时，对位移响应几乎没有影响。

调节电感数值，使电路固有频率分别为25 Hz、40 Hz、48 Hz、55 Hz、70 Hz（关于悬臂梁1阶固有频率对称），对其进行系统仿真，输出电压响应如图9所示。

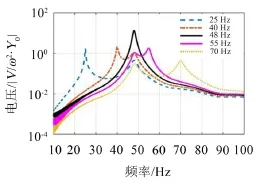
图9 不同电感工况下系统的输出电压

可以看出，调节电路固有频率，使电路固有频率与悬臂梁固有频率越接近，系统输出的电压响应越大；在两个固有频率一致时，系统输出电压只表现出一个峰值。

调节电路固有频率在机械系统固有频率附近变化，系统在不同频率下的输出电压和位移如图10和图11所示。

图10 不同电路固有频率下输出电压响应

图11 不同电路固有频率下位移响应

当电路的固有频率接近机械系统的固有频率时，系统的电压响应只有一个峰值，并且当电路固有频率在机械系统固有频率附近变化时，输出电压响应对电路固有频率的变化更为敏感；外激励频率与电路固有频率相同时，系统电压输出提高更为显著；电路固有频率的变化对系统位移几乎没有影响。

3.3 电路参数优化

由于电路元件可调节性远远高于机械系统，并且外激励与电路共振时，对系统电压的输出更为显著，因此在悬臂梁系统固有频率不变情况下，可尝试设计可调电路，使电路固有频率追踪外激励固有频率变化，以此来提高压电悬臂梁能量采集系统的能量输出效率。仿真外激励在20 Hz～70 Hz变化，若电感可追踪外激励频率，则系统输出电压如图12所示，可将系统采集效率维持在一个较高的水平。

图12 调节电路固有频率随外激励变化

4 结语

针对压电式振动能量采集器的机电耦合模型进行深入探讨，并基于两种不同的压电片电边界条件假设进行数学建模及仿真分析。发现在能量采集系统中，由于耦合较弱，电边界条件不明显，在两种电边界条件的假设下，系统输出基本一致；但反之，若以压电片作为驱动器的激振系统，两种电边界条件对系统输出估计差距较大，而通常此时，电压较强，均匀电压的电边界条件很容易判断。

同时仿真结果证明，压电悬臂梁在外激励频率远低于梁的第2阶固有频率的时候，可将悬臂梁简化成单自由度系统进行理论估计；对比发现，建立2阶能量采集电路，能较大程度地提高系统的能量采集效率。并且2阶电路的能量采集效率对外激励的频率更为敏感，若可通过调节电路固有频率一定程度上追踪外激励频率，对系统能量采集效率的提高也有较大帮助。

[1]ERTURK A,INMAN D J.On mechanical modeling of cantilevered piezoelectric vibration energy harvesters[J]. Journal of Intelligent Material Systems and Structures, 2008,19(11):1311-1325.

[2]王光庆.压电振动能量采集器的力电耦合模型及其功率优化[J].传感技术学报，2014，26(8)：1093-1100.

[3]ERTURK A,RENNO J M,INMAN D J.Piezoelectric energy harvesting from a L-shaped beam-mass structure with an application to UAVs[J].Journal of Intelligent Material Systems an Structures,2009,20(5):529-544.

[4]ERTURK A,INMAN D J.A Distributed parameter electromechanical model for cantilevered piezoelectric energyharvesters[J].JournalofVibrationand Acoustics,2008,130(4):041002.

[5]SODANO H A,PARK G,INMAN D J.Estimation of electric charge output for piezoelectric energy harvesting [J].Strain J.Brit.Soc.Strain Measurement,2004,40 (2):49-58.

[6]佘引.MEMS压电阵列振动能量收集器[J].传感技术学报，2014，27(8)：1033-1037.

[7]KIM J S.High-authority piezoelectric actuation system synthesisthroughmechanicalresonance，electrical tailoring[J].Journal of Intelligent Material Systems and Structures,2005，16(1):21-31.

[8]MEI JIE,TAO MENGLUN,XIAO HANBIN.Analytical simulation of the cantilever-type energy harvester[J]. Advances in Mechanical Engineering，2016,8(1):1-11.

[9]LI JINGCHENG.Optimization of piezoelectric energy harvester for wireless smart sensors in railway health monitoring[J].Processing of SPIE,2013,8692-86924L.

[10]龚俊杰.双晶悬臂梁压电发电装置发电能力的仿真[J].振动、测试与诊断，2014，34(4)：658-663.

[11]XU J,TANG J.Linear stiffness compensation using magnetic effect to improve electro-mechanical coupling forpiezoelectricenergyharvesting[J].Sensorsand ActuatorsA:Physical,2015,235:80-94.

[12]阚君武，唐可洪，王淑云，等.压电悬臂梁发电装置的建模与仿真分析[J].光学精密工程，2008，16(1)：71-75．

[13]刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势[J].振动与冲击，2012，31(16)：169-176.

[14]王宏金，孟庆丰.压电振动能量收集器的等效电路建模分析与实验验证[J].西安交通大学学报，2013，47(10)：75-80.

Model and DynamicAnalysis of the Electro-mechanical Coupling System of Piezoelectric Vibration Energy Harvesters

ZHANG Meng-qian,SONG Han-wen
(School ofAerospace Engineering andApplied Mechanics,Tongji University, Shanghai 200092,China)

Cantilever beams with piezoelectric ceramic layers have been frequently used as piezoelectric vibration energy harvesters.The most classical piezoelectric cantilever model d31of the piezoelectric energy harvesters(PEH)is studied in this paper.The exact analytical solution of the cantilever PEH is presented based on Euler-Bernoulli beam assumption.The influence of dynamic mode shape and strain distribution of the cantilever PEH is considered.The mathematical model of the cantilever PEH is established and the electro-mechanical coupling principle and characteristics are deeply analyzed with the two boundary conditions of uniformly distributed electric field and uniformly distributed electric displacement respectively.Based on the traditional PEH of order one,an inductance is added to the circuit to establish a second order circuit and improve the mathematical model.In the improved model,a new system with n+1 DOFs is obtained by combining the second order circuit with the n-DOF oscillatory system so that the global simulation of the coupled system can be realized.In addition,the influence of different elements of the circuit is analyzed.It is found that the added inductance can greatly increase the energy-harvesting efficiency of the PEH.

vibration and wave;vibration energy harvester;electro-mechanical coupling model;system simulation; power optimization

O32

A

10.3969/j.issn.1006-1355.2017.02.002

1006-1355(2017)02-0007-06+22

2016-11-08

国家自然科学基金资助项目（11272235）

张梦倩(1991－)，女，硕士研究生，上海市人，主要研究方向为压电振动能量采集。E-mail:09102mq@tongii.edu.cn

宋汉文，博士生导师。E-mail:hwsong@tongji.edu.cn