双向正交加筋板声振响应解析方法研究
李生,张安付,王真,黎申,游卓
(1.海军驻武汉七一九所军事代表室,武汉430205;2.武汉第二船舶设计研究所,武汉430205;3.武汉纺织大学机械工程与自动化学院,武汉430200)
双向正交加筋板声振响应解析方法研究
李生1,张安付2,王真3,黎申2,游卓2
(1.海军驻武汉七一九所军事代表室,武汉430205;2.武汉第二船舶设计研究所,武汉430205;3.武汉纺织大学机械工程与自动化学院,武汉430200)
提出双向正交加筋板声振响应的一种解析计算方法。使用两种连续性条件,建立双向正交加筋板的耦合振动方程。利用二维傅里叶级数作为双向正交加筋板振动位移表达式,将双向正交加筋板振动微分方程化为线性方程组,求解获得双向正交加筋板的模态特性以及加筋板稳态声振响应,并通过了现有文献数据和有限元方法的验证。通过进一步的参数分析,研究加强筋在板上的排布方式对加筋板声振特性的影响。
振动与波;双向正交加筋板;声振响应;任意边界条件;二维傅里叶级数
加筋板在工程各领域有着广泛应用,如航空器和船体的壁板。加筋板的振动和声学问题一直受到研究者和工程人员的关注。当加筋薄板结构受到外力激励,结构将产生振动并向外辐射噪声,结构过大的振动会影响到与之连接的仪器和仪表,会减弱仪器仪表的灵敏度,振动产生的噪声与会对人们的身体和生活产生不良影响。在早期加筋板振动的解析方法研究中,主要存在两种做法,一种是熟知的“正交异性板壳理论”[1–2],这种方法没有突出加强筋自然的离散特性,没有考虑加强筋与板之间力的相互作用,而是将加筋板看作一个整体结构,对于一些稀疏加筋、不等距、不均匀加筋,这种方法很难处理。二是将加强筋当成为刚性结构处理[3],但是这种处理方法与工程实际有较大差异。
随着研究的深入,研究者逐渐将加强筋作离散结构处理[4],即将加强筋作为加筋板的离散结构,利用加强筋与板结构之间连续条件,建立起筋-板力平衡关系。杨阳利用离散原理,提出一种加筋板机械导纳分频段计算方法[5]。Lorenzo Dozio等人提出一种可以方便编程、有较高计算效率的加筋方板振动特性解析-数值计算方法[6]。该方法适合带有小数量、轻加强筋平板的振动特性分析。Tian Ran Lin推导了带有周期或不规则加强筋的四边简支有限加筋板输入导纳的显式表达式,并分析了周期加筋或不等距加筋平板的振动控制机理和模态特性[7]。Anirban Mitra等人研究了带有初始变形加筋板的自由振动特性[8]。尽管目前各类解析方法可以用来研究各种形态加筋板振动特性,但仍存在各种不足,如只能处理经典边界条件、求解精度不高等。
文中亦将加强筋考虑为离散结构,在平板振动方程中加入加强筋的反力和反弯矩,建立双向正交加筋板的耦合振动控制方程,结合相应的边界条件,通过引入二维傅里叶级数作为位移假设函数,实现振动微分方程的矩阵化,求解加筋板的振动响应,并使用Rayleigh积分,获得双向正交加筋板的声辐射特性。Rayleigh积分是一种离散化求声场的手段,将振动辐射面离散为多个离散点声源,然后求和得到远场的声压。
1 理论研究
图1为双向正交加筋矩形板示意图,板上共有I根纵向加强筋与x方向垂直,共有J根横向加强筋与y方向垂直,加强筋与矩形板边界平行,加筋板四边边界条件任意。图1中EE表示加筋板为任意边界条件。
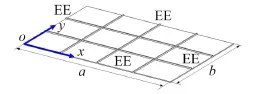
图1 双向正交加筋板示意图
根据平板和加强筋的位移连续、力平衡两种连续性条件,得到加筋板耦合振动方程为[6]

式(1)中集中力作用在点(x0,y0)上,方程等号左边前两项为平板的振动方程,第三、四项为横向筋与平板之间的相互作用力,第五、六项为纵向筋与平板之间的相互作用力,方程的右边为外激励力,可以为面激励力、线激励力、点激励力。文中以点激励力为例。式(1)囊括平板上的所有力,并将所有力联系在同一个方程中。
式(1)中,当右边为0表示自由振动方程,当右边为F0δ(x-x0)δ(y-y0)ejωt表示受迫振动方程。筋与平板之间作用力、扭转弯矩的表达式为

式(1)至式(5)中,i=1,2,…I,,j=1,,2,…J。分别表示第j根横向加强筋的弯曲刚度、翘曲刚度、扭转刚度、密度、截面积、极惯性矩表示第i根纵向加强筋的相应参数为双调和算子,δ为狄拉克函数。ω为圆频率,w(x,y)为矩形板的横向弯曲位移。加强筋在发生扭转变形时的转角θy(x,yj)和θx(xi,y)表示为

加筋板四条边界的边界方程为式(8)至式(11)[9],边界方程反映了加筋板在边界处力、弯矩的连续性,式(8)至式(11)中,kx0和kxa(ky0和kyb)为x=0和x=a(y=0和y=b)处的横向边界约束刚度,Kx0和Kxa(Ky0和Kyb)为x=0和x=a(y=0和y=b)处的扭转边界约束刚度,表达式的右边分别为加筋板在边界处的截面剪切力和弯矩。刚度k和K组成的外界弹性力(弯矩)和加筋板的截面剪切力(弯矩)构成了加筋板的边界方程。
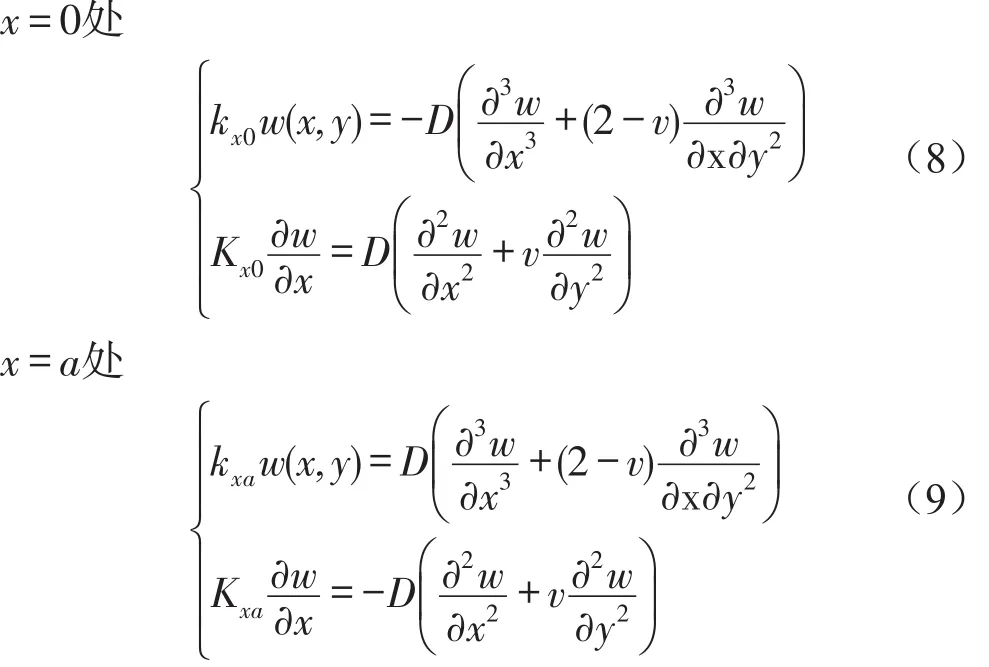
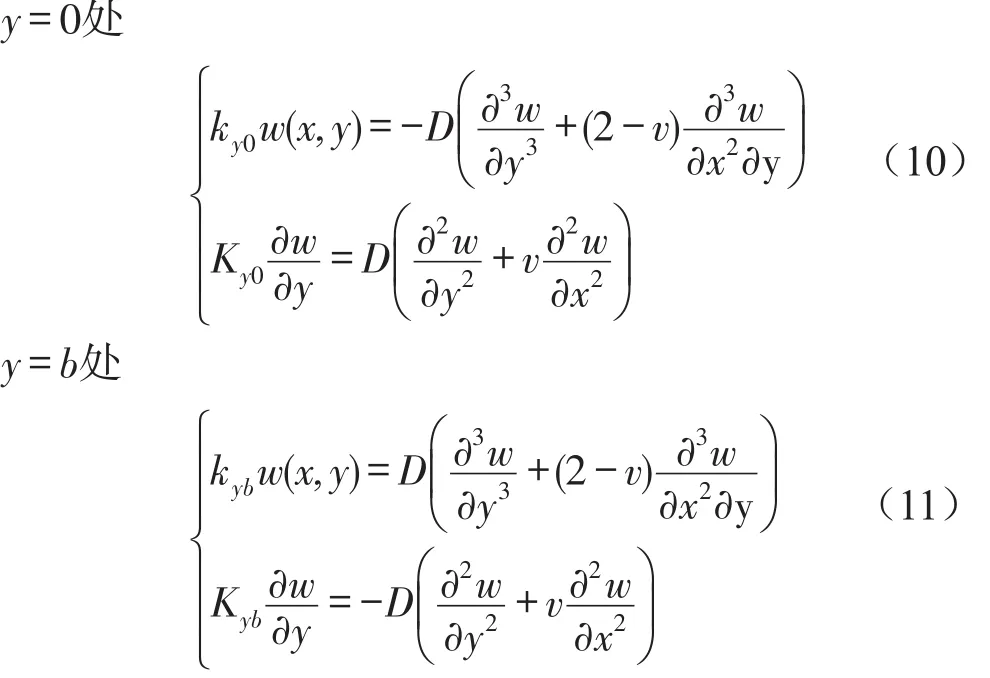
为了适应加筋板的任意边界条件,位移函数可以表达为二维傅里叶级数[9]

式中λam=mπ/a,λbn=nπ/b,在级数求和中,m的截断项数为M,n的截断项数为N,函数为一般的三角函数,表达较复杂,具体参阅文献[9]。式(12)的构造思路本质上利用了余弦级数在边界处不为零的特点,可以表达边界处任意幅值的位移。
将加筋板位移表达式(12)代入式(8)至式(11)边界方程,并沿边界长度进行积分,消去位置变量x、y,使边界方程可以写成矩阵的形式,如下所示

式中矩阵H和Q均为边界方程经过整理得到的常量矩阵。矢量p和a分别为
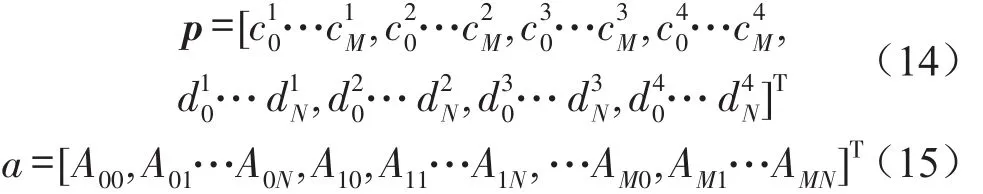
同样将位移表达式(12)代入加筋板的振动控制方程式(1)中,去微分符号,并沿整个板面进行积分,消去位置变量x、y,写成矩阵形式为

利用式(13)得到p=H-1Qa,并代入式(16)消去矢量p。由于八个边界方程相互独立,故矩阵H确定可逆。得到更简洁的线性方程组为

若加筋板受外激励力,根据式(1)中的受迫振动方程,受迫振动线性方程组可以表达为

式(18)中外激励矢量F的元素为
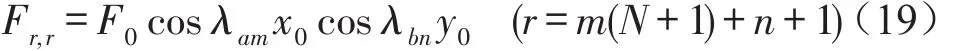
阻尼矩阵C为比例阻尼,表达式如下

σ1为质量矩阵因子,σ2为刚度矩阵因子。
通过求解式(17)即可以得到加筋板的模态特性;通过求解式(18)可以得到a中的元素,再将a代入式(13)可以得到p,将a、p代入振动位移表达式(12),则即可获得加筋板在点激励力作用下的振动位移。
根据计算得到的加筋板振动响应,由瑞利积分可以求得加筋板的辐射声功率为[10]

ve为板振动速度矢量,rij(i=1,..L,j=1,...L)为板上两点之间的距离,k=ω/c0,ρ0为辐射声场介质的密度,c0为声场介质的声速,Ae为板上被分割小块的面积,L为板上被分割小块的数量。
根据板的辐射声功率和振动速度,可以由式(23)计算得到加筋板的声辐射效率。

式中S为加筋板的辐射面积,vˉ为加筋板的平均均方振速。
2 计算分析
2.1 数值方法验证
通过文献[6]中已有的算例来验证本解析方法的有效性,图2给出了文献中一个算例的双向正交加筋板示意图,该加筋板含两个纵筋和两个横筋。板结构和加强筋的材质均为钢。板尺寸a=2 m,b=1 m,厚度为10 mm,所有筋高均为15 mm,筋宽为10 mm。

图2 两横筋两纵筋加筋板示意图
表1给出了图2中加筋板结构前5阶归一化固有频率值随位移假设函数的截断常数M、N的变化,归一化固有频率的计算公式可参见文献[6]。可以看出,M=N=9时,结果基本收敛,显示了很好的收敛性。同时与该文献中算例的归一化固有频率结果数据作对比,验证了本解析方法具有较高的精度。

表1 采用本解析方法计算所得加筋板固有频率的收敛性和精度
以下算例仿真验证本解析方法计算双向正交加筋板振动响应的有效性,加筋板x方向均布三根纵向筋,y方向均布两根横向筋,板长1.6 m,宽0.9m,厚4 mm,所有加强筋均有相同的截面尺寸,宽10 mm,高15 mm。加强筋和平板的材质设为钢。选取加筋板上(0.5 m,0.4 m)位置为激励点,拾取加筋板上激励位置、(1.0 m,0.5 m)位置处振动速度,计算中加筋板的边界条件分别为经典(固支)、任意边界条件。为了作对比验证,建立加筋板的有限元模型,模型采用Beam188和Shell181单元表征加强筋和平板。
经典(固支)、任意边界条件下加筋板输入和传递速度导纳本文理论分析结果与Ansys有限元结果对比如图3、图4所示。

图3经典边界条件下加筋板振速响应
图3和图4给出了加筋板的输入速度响应和传递速度响应。边界分别为经典(固支)和任意边界条件,可以看出本文理论解析方法所得结果与有限元仿真值吻合相当好,验证了本解析方法在计算加筋板振动响应时有较高精度。

图4 任意边界条件下加筋板振速响应
2.2 加强筋排布方式的影响分析
为了分析加强筋位置对加筋板声振响应的影响,这里引入三种类型的加筋排布,分别为中心密集、均匀和稀疏排布,如图5所示。
三种排布方式中加强筋间距均为等差数列,公差分别为∓70 mm、0 mm、±70 mm。纵筋6根,横筋2根,板尺寸为1.2 m×0.9 m×0.005 m,加强筋的尺寸为15 mm×5 mm,激励点在板的中心位置附近,坐标为(0.6 m,0.47 m)。分别计算结构的振动能量以及辐射声功率和辐射效率。振动能量定义为板均方振速平方与板质量的乘积的一半。
从图6-图8可以看出,加强筋的排布方式对加筋板结构振动和声辐射有一定的影响。加强筋向中心激励点集中,可使得加筋板的低阶共振声响应增强,也增强了加筋板的低频声辐射效率。密集排布由于增大了激励点区域的刚度,使加筋板在低频段振动响应有所降低。
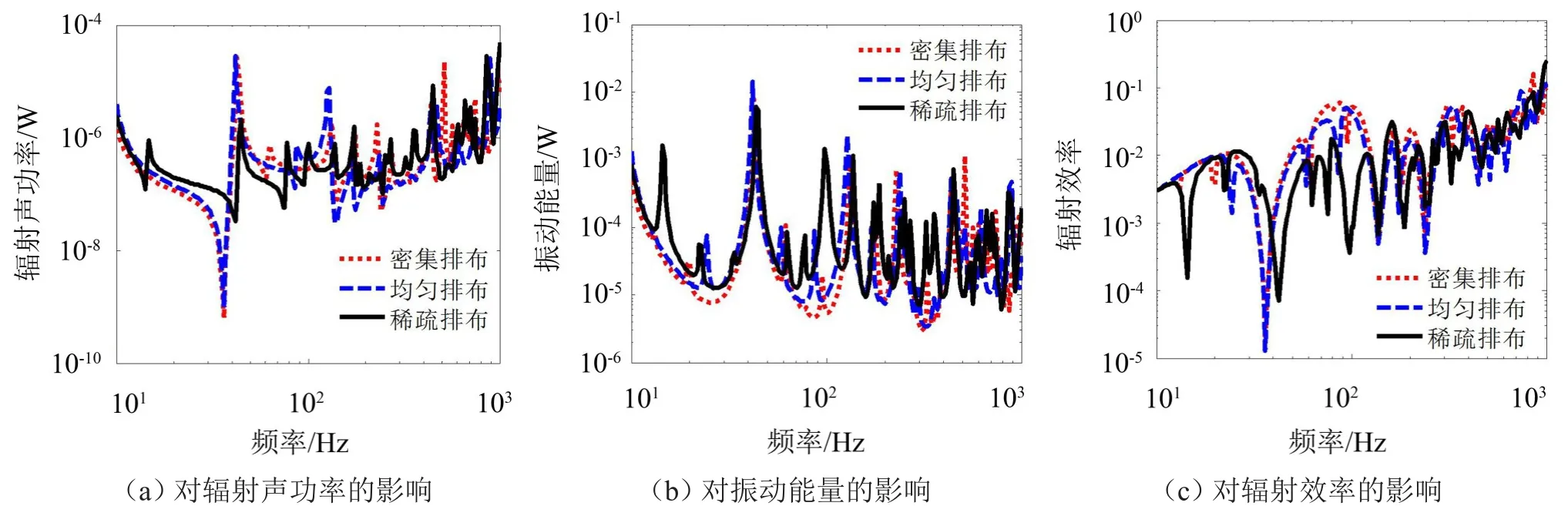
图6 加强筋排布方式对加筋板声振响应的影响
3 结语
提出一种求解任意边界条件下双向正交加筋板振动和声响应的解析方法,使用二维傅里叶级数为加筋板假设位移表达式,通过求导、积分,将加筋板振动方程的微分符号消除,得到相应的线性方程组,求解获得加筋板的模态和稳态响应,并使用Ansys有限元软件验证了该解析方法的有效性和精度。
利用建立的加筋板解析模型,讨论加强筋在板上排布方式对加筋板振动、声响应的影响,结果表明:加强筋的排布方式对加筋板声振响应有明显影响,加强筋越向激励点集中,低频段加筋板的声功率就会越大,而振动能量会越减小,从而使加筋板的低频辐射效率越大。
[1]MUKHERJEE A,MUKHOPADHYAY M.A review of dynamic behavior of stiffened plates[J].The Shock and Vibration Digest,1986,18(6):3-8.
[2]任惠娟,盛美萍.加筋矩形薄板的平均声辐射效率[J].振动与冲击,2016,35(20):167-171.
[3]MUKHOPADHYAYM,MUKHERJEEA.Recent advances on the dynamic behavior of stiffened plates[J]. The Shock and Vibration Digest,1989,21:6-9.
[4]陈晓利,盛美萍,王彦琴.多筋板振动特性的导纳法研究[J].噪声与振动控制,2005,25(3):9-12.
[5]杨阳.加筋板机械导纳分频段计算方法[J].噪声与振动控制,2016,36(3):42-47.
[6]LORENZODOZIO,MASSIMORICCIARDI.Free vibrationanalysisofribbedplatesbyacombined analytical-numerical method[J].Journal of Sound and Vibration,2009,319:681-697.
[7]TIAN RAN LIN.A study of modal characteristics and the control mechanism of finite periodic and irregular ribbed plates[J].Journal of the Acoustical Society of America, 2008,123(2):729-737.
[8]ANIRBAN MITRA,PRASANTA SAHOO,KASHINATH SAHA.Free vibration analysis of initially deflected stiffenedplatesforvariousboundaryconditions[J]. Journal of Vibration and Control,2011,17(14):2131-2157.
[9]W L LI,XUEFENG ZHANG,JINGTAO DU,et al.An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports [J].Journal of Sound and Vibration,2009,321:254-269.
[10]MIGUEL C.JUNGER,DAVID FEIT.Sound,structures, and their interaction[M].London:The MIT Press,1986: 75-272.
Research onAnalytical Method for Vibro-acoustic Response Analysis of Bi-directionally Orthogonal Stiffened Plates
LISheng1,ZHANG An-fu2,WANGZhen3LIShen2,YOUZhuo2
(1.Military Representative Office,Navy Stationed in 719 Research Institute,Wuhan 430205,China; 2.Wuhan Second Ship Design and Research Institute,Wuhan 430205,China; 3.School of Mechanical Engineering andAutomation,Wuhan Textile University, Wuhan 430200,China)
The analytical method for sound and vibration analysis of bi-directionally orthogonal stiffened plates is proposed.By using displacement and force continuity conditions between plates and stiffeners,vibration equations of the stiffened plate system are established.With the displacement function expressed as a two-dimensional Fourier series,one can convert the differential equations of the stiffened plates into linear algebraic equations.Thus,the solutions of free vibration and forced vibration of the stiffened plates can be obtained.Results of the present method demonstrate a good agreement with published results and the results of typical finite element analysis.Subsequently,the effect of stiffeners position on vibro-acoustic response of multi-stiffened plates is studied.
vibration and wave;bi-directionally orthogonal stiffened plate;vibro-acoustic response;arbitrary boundary conditions;two-dimensional Fourier series
O326;TB532
A
10.3969/j.issn.1006-1355.2017.02.004
1006-1355(2017)02-0018-05
2016-09-29
国家自然科学基金资助项目(11202152)
李生(1979-),男,山东省泰安市人,工程师,主要研究方向为船舶性能。E-mail:li_s_li@sina.com
张安付(1986-),男,安徽省六安市人,博士,工程师,主要研究方向为振动与噪声控制。E-mail:anfu1769@163.com

