激活学生思维的几点感悟——以“导数”情境教学为例

☉山东省邹城市实验中学 李现勇

激活学生思维的几点感悟
——以“导数”情境教学为例

☉山东省邹城市实验中学 李现勇

情境教学是指教师根据教学目的需要，从教学内容出发创设问题情境，通过体验情景、思考、质疑，学生自觉地发现问题、提出问题；在合作讨论、感知努力和教师适时诱导、鼓励下，解决问题；在课堂练习应用的基础上，实现对所学知识的巩固与提升.本文以导数教学中的情境创设为例加以说明.

一、情境导入，引起“认知冲突”

情境1对于基本初等函数的单调性，我们都非常熟悉，如指数函数或对数函数，当底数大于1时，在定义域内单调递增；在底数小于1时，单调递减.那么对于一个初等函数，如（fx）=x3-2x2-5x+1，我们如何来判断它的单调性？

一次函数（fx）=kx+b是我们非常熟悉的函数，其单调性可由k为确定：当k＞0时，函数单调递增；当k＜0时，函数单调递减.

在这里斜率k起到了关键的作用.那么对于其他的函数，我们能否找到一条与函数单调性有关的直线，利用其斜率判断该函数的单调性呢？

在这里学生自然想到了曲线的切线，如图1和图2所示.

图1

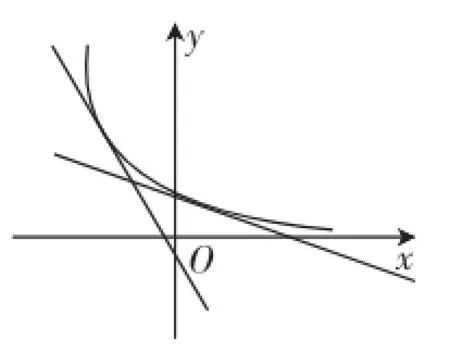
图2

由图1和图2我们不难发现：若一个函数为增函数，则在该函数图像上任一点的切线的斜率均大于0；若一个函数为减函数，则在该函数图像上任一点的切线斜率均小于0.

那么反向思考，欲判断一个函数在某一区间内的单调性，若在该区间内任取一点（x0，f（x0）），如果我们能够判断在该点的切线斜率的正、负，是不是就可以判断此函数的单调性了？

二、探索新知，启发“感悟发现”

直线AB与函数图像有两个交点，相对于切线来说，我们不妨称之为割线，那么接下来我们看看切线与割线有什么关系？

如图3，设切线与割线有一个公共点B，什么情况下割线就会变成切线呢？不难发现：当点A向点B靠近，即x1无限接近x2时，两直线重合.

图3

从而引出教材中的导数定义：

设函数y=f（x）在x0及其附近有定义，当自变量在x=x0附近改变量为Δx时，函数值也相应地改变，即Δy=f（x0+ Δx）-f（x0）.

函数f（x）在点x0的瞬时变化率，通常称为f（x）在点x0处的导数，记作f′（x0），即f′（x0）

情景3我们要想利用切线的斜率来判断一个函数的单调性，只求函数图像在某一点处的切线斜率能实现吗？

例1求抛物线f（x）=x2在x=1处的导数f′（1）.

例2已知f（x）=x2，求f′（x）.

例3求函数f（x）=x2的单调区间.

解析：由例2知，f′（x）=2x.

当x＞0时，f′（x）＞0；当x＜0时，f′（x）＜0.

所以函数f（x）的单调递增区间为（0，+∞），单调递减区间为（-∞，0）.

三、应用拓展，鼓励“质疑问难”

教材例题节选：

例4求抛物线y=x2在点（1，1）处的切线斜率.

解析：由例1可知，抛物线在点（1，1）处的切线斜率是2.

情景4如果已知条件所给的点（a，b）不在函数曲线f（x）上呢？即求曲线过某一点的切线，如何处理？生：设切点坐标为（x0，f（x0）），可求得切线的斜为k=f′（x0）.①

又因为切点也在切线上，可得

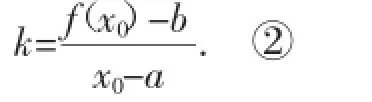
联立式①②，即可求出切点坐标，从而求出切线斜率及方程.

由例3可知，抛物线在点（x0）处的切线斜率为2x0.

故切点为（2，4），（3，9），

所以切线方程为y=4x-4，y=6x-9.

四、规律发现，培养“自我反思”

某些基本初等函数的导数公式，在高中范围内是无法利用导数的定义求出，因此可利用归纳推理的办法，由学生自行得出，从而使新知识的引入更顺畅、自然.

例6已知函数f（x）=x3，求f′（x）.

由例2得（x2）′=2x，思考一下，有何规律？能否得到（xn）′=？

不难得出幂函数的求导公式，即（xn）′=nxn-1.

由此引出其他基本初等函数的求导公式及运算法则（略）.

解析：求导得f′（x）=x2-4x-5=（x+1）（x-5）.

令f′（x）=0，得x=-1，x=5.所以，

当x＜-1或x＞5时，f′（x）＞0，所以f（x）单调递增；

当-1＜x＜5时，f′（x）＜0，f（x）单调递减.

所以函数f（x）的单调递增区间为（-∞，-1）和（5，+∞）；单调递减区间为（-1，5）.

综上，对于一个新知识点的学习，如何让学生接受起来更自然？毫无疑问，从学生熟悉的知识入手是行之有效的策略.因此在新知识的学习之初，教师要善于从学生熟悉的角度创设情境，在问题情境中，引发学生独立探究、发现问题、提出问题，通过学生的合作讨论、教师的适时诱导，学生自主建构知识，形成师生和谐互动的教学氛围，使学生轻松、主动的学习，使不同能力的学生获得成功的体验，接受和谐文化环境陶冶，感受人文关怀，不断提升自主学习能力和创新意识，使学生顺利实现新、旧知识的过渡.本文以导数教学为例，从问题情境设置的角度入手，层层递进，展开新知识点的教学.