问题审视的几个关键点

☉江苏省常熟市尚湖高级中学 江 政

问题审视的几个关键点

☉江苏省常熟市尚湖高级中学 江 政

审题是解题的关键环节，问题的求解，都是从审题开始的.那么审题都审什么？

1.审条件

条件是题目直接给出的信息，是我们解题的依据，但这里的条件，不仅仅是直接给出的条件，还有隐含的条件，即由所给条件直接或间接得出的一些结论，都是条件，这些条件往往是我们解题的关键部分.

2.审结论

所求的结论是什么？结论与条件有什么关系？结论的求解有哪些方法？针对这一结论，哪一个方法才是最合适的方法？

下面以导数背景下的不等式恒成立问题为例，说明问题审视中的几个关键点.

例1已知函数f（x）=lnx-a·sin（x-1），其中a∈R.

（1）如果曲线y=f（x）在x=1处的切线的斜率是-1，求a的值；

（2）如果f（x）在区间（0，1）上为增函数，求a的取值范围.

一、通过审题明确问题的本质

导数是研究函数单调性的有力工具，利用导函数的正负可判断函数的增减.本题第（2）中条件所给的是“f（x）在区间（0，1）上为增函数”，即“f′（x）≥0在区间（0，1）上恒成立”，则问题转化为不等式恒成立问题.而不等式恒成立问题的求解，通常转化为函数最值问题处理，即构造目标函数，求函数最值.本题已知函数关系式中含有三角式，则问题求解中要注意三角函数有界性的应用.

解析：（1）略.

（2）因为f（x）在区间（0，1）上为增函数，

所以对于任意x∈（0，1），

令g（x）=x·cos（x-1），

所以g′（x）=cos（x-1）-x·sin（x-1）.

因为x∈（0，1）时，sin（x-1）＜0，所以x∈（0，1）时，g′（x）＞0，g（x）在区间（0，1）上单调递增，

所以0＜g（x）＜g（1）=1.所以a≤1.

故a的取值范围是（-∞，1］.

评析：本题的求解中借助了“二次求导”，即提取函数解析式的一部分，再进行求导、求最值.

二、通过审题理解知识的发散性

上例的解答中对不等式恒成立问题的处理，关键环节是构造函数，对于较基础的问题可通过移项、合并，直接构造.本题采用的是先分离参数，再构造函数，其中分离参数是问题求解的关键.但针对不同的问题，构造函数的方式往往不同，如：

例2设函数（fx）=xlnx.

（1）求证：（fx）≥x-1；

（2）若（fx）≥ax2+（a≠0）在区间（0，+∞）上恒成立，求a的最小值.

解析：（1）证明：要证f（x）≥x-1，只需证明g（x）= xlnx-x+1≥0在（0，+∞）恒成立，g（′x）=lnx+1-1=lnx.

当x∈（0，1）时，g（′x）＜0，g（x）在（0，1）上单调递减；

当x∈（1，+∞）时，g′（x）＞0，g（x）在（1，+∞）上单调递增.

故当x=1时，g（x）min=g（1）=1·ln1-1+1=0，

g（x）=xlnx-x+1≥0在（0，+∞）恒成立.

所以（fx）≥x-1.

（2）不等式xlnx≥ax2+在区间在（0，+∞）恒成立，等价于lnx≥ax+在（0，+∞）恒成立，等价于h（x）=lnxax-≥0在（0，+∞）恒成立.

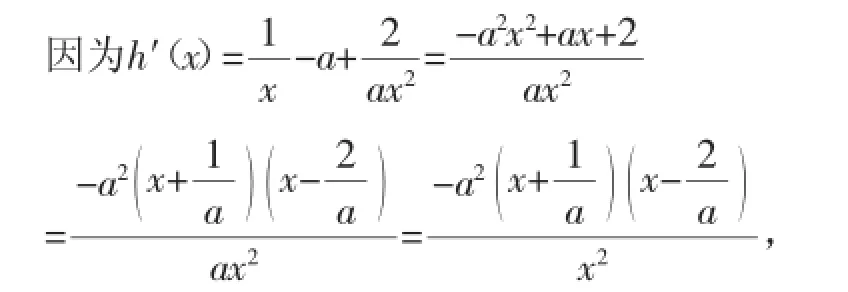
所以-e3≤a＜0，得到a的最小值为-e3.

评析：对于本题，要使xlnx≥ax2+在区间（0，+∞）上恒成立，无法分离出参数，若通过移项、合并，直接构造函数g（x）=xlnx-ax2+，求导得g（′x）=lnx+1-2ax，导函数的零点无法求出，不易判断函数的单调性.事实上以ex，lnx为背景的导数综合题是一类常见题型.如含有lnx的函数，若为分式结构，不论lnx在分子还是在分母的位置，导函数中依然含有lnx，这样为导函数零点的求解带来困扰.所以含有lnx的式子在等价变形时，要注意尽量将lnx分离出来，使lnx独立成一项，这样求得的导函数中不含lnx.相反，对于含有ex的函数，考虑导数乘法、除法的求导法则以及（e）x′=ex，在等价变形时，要注意综合ex，使其他项与ex相乘或相除的运算作为一项.这样求导后，可以提取公因式ex，它的符号恒正，再对余下多项式函数进行讨论即可.

例3设函数（fx）=aex-x-1，a∈R.

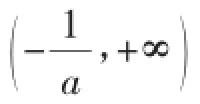
解析：（1）因为ex＞0，所以（fx）=aex-x-1＞0恒成立，等价于a＞恒成立.

当x∈［0，+∞）时，g′（x）≤0，

所以g（x）在［0，+∞）上单调递减，

所以x∈（0，+∞）时，g（x）＜g（0）=1.

设h（x）=ex-xe-1，x∈［0，+∞）.

三、通过审题关注思想的深刻性

导数背景下不等式恒成立问题的求解，关键是构造函数，但构造函数的方式，根据不同的题型，构造的方法可能是多种多样.如例1采用的方法是分离参数后构造函数，例2采用的方法是分离lnx后构造函数，例3采用的方法是由对数不等式中提取出函数的方法.因此构造时，不要拘泥于某一类型，要具体问题具体分析.如：遇到形如不等式ex≥f（x）恒成立的类型，学生往往会采用作差比较法构造函数，即ex-f（x）≥0的形式，然后构造函数φ（x）=ex-f（x），再通过分情况讨论，来逐步解决.但这种做法往往需进行较复杂的讨论.

在学习不等式时，我们都知道：在证明不等式A＞B时，如果B＞0，可以考虑作商比较转化为证明＞1成立.因此在研究不等式ex≥（fx）时，由于ex＞0恒成立，同样也可以考虑作商比较把ex≥（fx）变形为≤1，然后构造函数φ（x）=，接下来只需保证函数φ（x）的最大值小于或等于1即可.

总之，在解题过程中要准确审视、合理利用条件，明确问题的求解类型，把握条件与结论之间的关系，正确选用合理的方法，实现问题的快速解答.