巧思“辩”解回归本质

☉江苏省白蒲高级中学 杨雪梅

巧思“辩”解回归本质

☉江苏省白蒲高级中学 杨雪梅

解题教学的初衷是教会学生用知识解决数学问题，但是越来越多的试题、不加思考的训练让教学很少有时间思考我们的教学是否需要做到“回头一瞥”！回顾近年来各地高考真题，我们不难发现不少优秀试题都在呈现一种信息：尽可能选拔出思维出众，而让通过大量做题获得熟练度而得到高分的学生不占优势.现阶段有一种不良的教学习惯：不少教师用大量解题训练替代思维训练，用教辅资料提供的答案给予学生，让机械成为学习数学的主流，让思维渐渐钝化.这种教学方式是要不得的.因此笔者以为回顾数学解题，教师更要教会学生巧思“辩”解，回顾本质.

一、返璞归真，追寻本质

基本知识和基本技能的考查总是以不同的方式呈现出来，有些能一眼看出想考查的是什么，有些则看着让人有些摸不着头脑.我们要一层一层拨开迷雾，发现问题的本质和考查的目标.

问题1已知递增数列｛a｝n，Sn为数列｛an｝的前n项和，S7＞7，S9＜18，则a8的取值范围是__________.

答案：1＜a8＜5.

744数列得a8＞a4＞1.从S9＜18，可得a5＜2，但无法将它和a8的范围直接联系起来.”

不少初学者在等差数列里面，利用性质和公式不断地尝试，都不能很快地得到结果.当我们思路不清时，不如寻找该知识点最本源的一些东西，比如定义、定理等.

学生一看到这一组式子恍然大悟，原来考查的是运用线性规划求范围.

给出基本问题，请学生再思考：已知函数f（x）=ax2+ bx-1（a＞0）有两个零点，其中一个零点在区间（1，2）内，则a-b的取值范围是__________.（答案：（-1，+∞））.

二、巧思过程，呈现本质

学生做完题，总是有这样的想法，做出来了就万事大吉了，一般不会再回头去看看、研究研究，总是盯着那些自己做错的题目.而将错题订正对了以后，也不关心为什么原来错了，后来订正的方法是不是最好的呢，有没有更好的呢？为什么这样的方法是最适合这个问题的？学生很少有这方面的想法，所以有很多题目虽然做过了，订正过了，但是再做时还是会错.学生也很困惑，不得其解.教师要引导学生对题目过程的回顾，从回顾比较中得出最优的方法，更重要的是得到题目的精髓，在这样的细致回顾和研究中才能提升学生的能力.

问题2已知函数f（x）=ax2+lnx（x＞0），g（x）=x3+（a-2e）x2+（a+e2）x（其中e为自然对数的底），试讨论函数H（x）=f（x）-g（x）的零点的个数.

分析：这个题目是某综合练习的最后一题的第二小题，大部分学生只进行了部分的计算，在令H（x）=0后得到等式：lnx-x3+2ex2-e2x-ax=0，继而学生选择了不同的路径来处理这个方程解的问题.

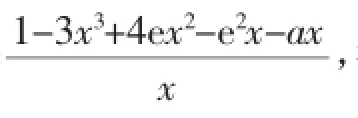
图1

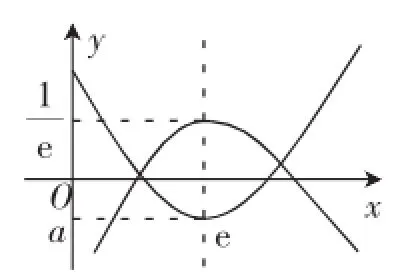
图2

学生丙的方法：采用变量分离，将lnx-x3+2ex2-e2xax=0整理成：a=-（x-e）2.

max

学生丁的方法：将lnx-x3+2ex2-e2x+ax=0整理成=（x-e）2+a，然后和学生乙采用两个函数交点个数的方法得到零点的个数.令两个函数μ（x）=和ν（x）=（x-e）2+ a.由于μ′（x）=则可以清楚地判断出μ（x）在（0，e）上单调递增，在（e，+∞）上单调递减，μ（x）=μ（e）=.结合

max图像2判断出结果.

学生评价：同学甲的方法最难实施下去，后三位同学虽然都得到了正确的结果，但是同学丁的方法最简洁，计算量最小.请学生思考：如果你是命题者，怎样才能命制出我们研究的这道题目呢？

再复杂的问题也是通过简单的基础知识进行转化和包装得到的，只要将这层层包装打开，就能看到问题的本质，其实它们也许很简单.我们要善于挖掘出命题者的真实意图，这样做题才能有针对性，才能化繁为简，从内在提升学生的解题能力.

三、“辩”解计算，思考本质

解析几何问题侧重的是运算能力的考查，但是运算能力的考查也不是一味的死算，其中也必有算理和算法！笔者发现，学生在问题解决过程中并未能找到恰当的算理算法，而是一味的死算，导致陷入计算的泥潭！下面是典型的一例：

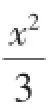
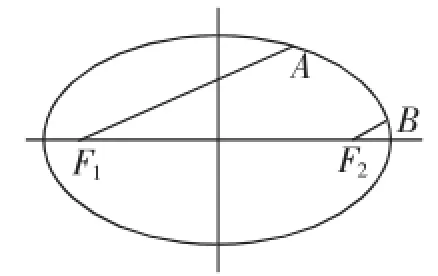
图3

图4

分析：本题是一道非常优秀的解析几何小题.但是从学生思考的角度来看，很少有学生能思考问题的本质.原因在哪里呢？我们不妨先看下标准答案提供的解答：

标准解答：设直线AF1斜率为k（k＞0），则直线AF1方程为y=k（x+），联立椭圆x2+3y2=3，得

辨析：参看标准解答，我们不难发现，这样的解答方式并不是我们想要的，也不可能在短短的应试中完成的.究其原因：第一，解答过程违背了解析几何求解的第一原则——“设而不求”，求点坐标是解析几何万不得已的方式，是问题解决的大忌，如此烦琐的运算和呆板的算理，笔者认为学生基本是放弃的.那么教师要引导学生思考本题考查的到底是什么呢？到底要在哪里体现解析几何考查的本质呢？让我们静心回想下椭圆中这两条线段所呈现的关系？

师：抛开这个问题，我们回想下，椭圆本身具备何种对称性？与过焦点的直线相交，这种对称关系还具备吗？

生：椭圆具备中心对称和轴对称，过焦点的直线具备了中心对称的性质.哦！我发现了，只要利用中心对称的性质，如图4，将线段BF2对称到B1F1，问题迎刃而解！

故点A的坐标是（0，±1）.

通过本题的分析与解，我们发现本题其实考查了椭圆中最基本的一个性质——中心对称性！可以这么说，这是椭圆第一课时就向学生介绍，所有师生都非常熟悉的一个基本性质，但是在问题掩盖的背后，还有多少学生能想到问题所要考查的本质呢？所以笔者以为，解题不能一味参看标准解答，要多思考问题背后所呈现的教材中的基本知识和基本性质，这才是数学学习的意义所在！对教辅资料而言，笔者想说尽信其不如无书！巧思“辩”解，回顾本质，才是教学需要面向的！

1.董成勇.一类解析几何问题的解决［J］.数学通报，2014（4）.

2.罗增儒.解题反思二则［J］.中学数学教学参考（上旬刊），2011（12）.

3.王志峰.从导数运算的一题多解中思考［J］.数学教学研究，2015（2）.