有界不确定结构基于最小二乘支持向量机回归的动力特性分析方法

莫延彧, 郭书祥, 唐 承

(1. 空军工程大学 航空航天工程学院, 西安 710038; 2. 空军工程大学 理学院, 西安 710051)

有界不确定结构基于最小二乘支持向量机回归的动力特性分析方法

莫延彧1, 郭书祥2, 唐 承2

(1. 空军工程大学 航空航天工程学院, 西安 710038; 2. 空军工程大学 理学院, 西安 710051)

针对不确定结构的动力特性分析问题展开研究，考虑仅已知结构参数变量变化范围的情况，建立不确定参数变量的区间模型。对不确定变量在其取值范围内进行改进的均匀试验设计抽样，并基于确定结构动力特性分析的有限元法和模态叠加理论，提出改进均匀试验设计抽样模拟方法；考虑到该算法计算效率较低，对其进行改进并提出基于最小二乘支持向量机回归的模拟方法，算法在不改变样本点数量的前提下，引入了支持向量机回归代理模型，用训练后的代理模型对不确定结构的动力特性进行了模拟分析。算法通过两个数值算例验证了其有效性。

均匀设计; 区间模型; 频率分析; 频响分析; 支持向量机回归

考虑到工程实际中制造工艺水平，材料特性多样性以及模型简化等因素，不确定性是普遍存在的，具体到结构中，主要体现在材料参数、几何参数和外载荷等参数变量的不确定性。因此，在解决结构的分析和设计问题时，特别是当对产品设计和模型细节的数学描述不够明确时，将其视作不确定结构更符合工程实际。传统的处理不确定问题的方法主要是对不确定参数进行随机化或模糊化，为使随机分布或隶属函数较为准确可靠，这两种方法需要较多的数据支持[1]。因此对于仅已知参数取值范围的有界不确定变量，随机化和模糊化并不适用，而基于区间模型的非随机方法则可以较好的解决有界不确定问题。

结构动力特性分析问题在工程实际中具有很广泛的应用，它是结构分析设计的重要部分。传统的结构动力特性分析主要针对确定性结构，其中参数变量都是确定的，这种分析问题可以用有限元方法较好的解决。而当考虑结构的有界不确定性时，其中部分参数是有界不确定变量，此时，用传统的有限元方法解决结构动力特性分析问题会变得非常困难。近期，有学者对此问题展开研究，王登刚[2]把具有有界不确定参数结构的固有频率所在区间范围问题转化为两个全局优化问题，并用实数编码遗传算法求解；张建国等[3]提出了一种求解有界不确定结构固有频率的区间逐步离散的方法；马梁等[4]利用Epsilon算法求有界不确定结构参数有大变化时的固有频率,得到频率的上﹑下界； MANSON[5]用复杂仿射分析方法计算有界不确定结构的频响函数，解决了普通区间运算扩张的问题； GERSEM等[6]用区间和模糊有限元方法求解有界不确定结构的固有频率和频响函数； MUNCK等[7]针对求解有界不确定结构频响函数的区间和模糊有限元方法存在的不严密性，提出一种基于响应面的优化技术；YANG 等[8]提出一种求解有界不确定结构动态响应的Laplace变换方法；MA 等[9]结合区间数学与模态综合法，求解了有界不确定转子结构的频响函数变化范围；SOFI等[10]针对线性无阻尼有界不确定结构，提出一种解决振动分析中广义区间特征值问题的有效方法。本文针对有界不确定结构频率和频响范围的分析计算展开研究，首先给出了一种基于改进均匀试验设计的模拟方法，后对其进行进一步改进，给出了基于最小二乘支持向量机(Least Squares Support Vector Machine, LS-SVM)回归的模拟算法，并对算法进行了验证。

1 确定结构基于有限元的动力特性分析

有限元法(Finite Element Method，FEM)是一种解决结构静态和动力特性分析问题的有效手段。通过FEM，复杂结构可以被划分成有限个较为简单的单元，从而可以通过对有限单元的整合去研究一个复杂结构的动力特性。

考察自由度为n的无阻尼结构，其动力学平衡方程可表示为

(1)

式中：K(∈Rn×n)为整体刚度矩阵；M(∈Rn×n)为整体质量矩阵；u(ts)为n维位移向量；F(ts)为n维力向量。K和M由FEM整合计算得到。

1.1 频率分析

考虑上述无阻尼结构自由振动的情况，由于式(1)中整体刚度和质量矩阵K和M已经通过FEM计算得到，因此第t阶自然频率ωt和与之相对应的第t阶标准振动模态Ut可以通过解决如下的特征值问题得到

(K-ω2M)u(ts)=0

(2)

式中：ω为频率；u(ts)为位移向量。

式(2)中的代数特征值问题可以用现有的商业软件(比如Matlab)计算解决，对其详细计算过程这里不做过多的介绍。

1.2 频响函数计算

通过求解式(2)中的代数特征值问题可得到t阶标准振动模态Ut，对其进行归一化得到归一化标准振动模态Ut norm，满足如下条件

(3)

和

(4)

对确定结构，K和M是确定的，因此归一化标准振动模态Ut norm是唯一的。根据模态叠加理论，考虑前m个模态叠加，则自由度j和k间频率响应函数(Frequency Response Function，FRF)可表示为

(5)

式中：FRFtjk为第t阶模态对自由度j和k间频率响应函数FRFjk的贡献；Ut norm,j和Ut norm,k分别为第t阶归一化标准振动模态Ut的第j和k分量。 式(5)中FRFjk可以进一步表示为

(6)

其中，Pt为Ut norm,j和Ut norm,k的乘积

Pt=Ut norm,j·Ut norm,k

(7)

考虑到确定性结构归一化标准振动模态Ut norm的唯一性，Pt为确定值。

2 基于均匀设计抽样的模拟方法

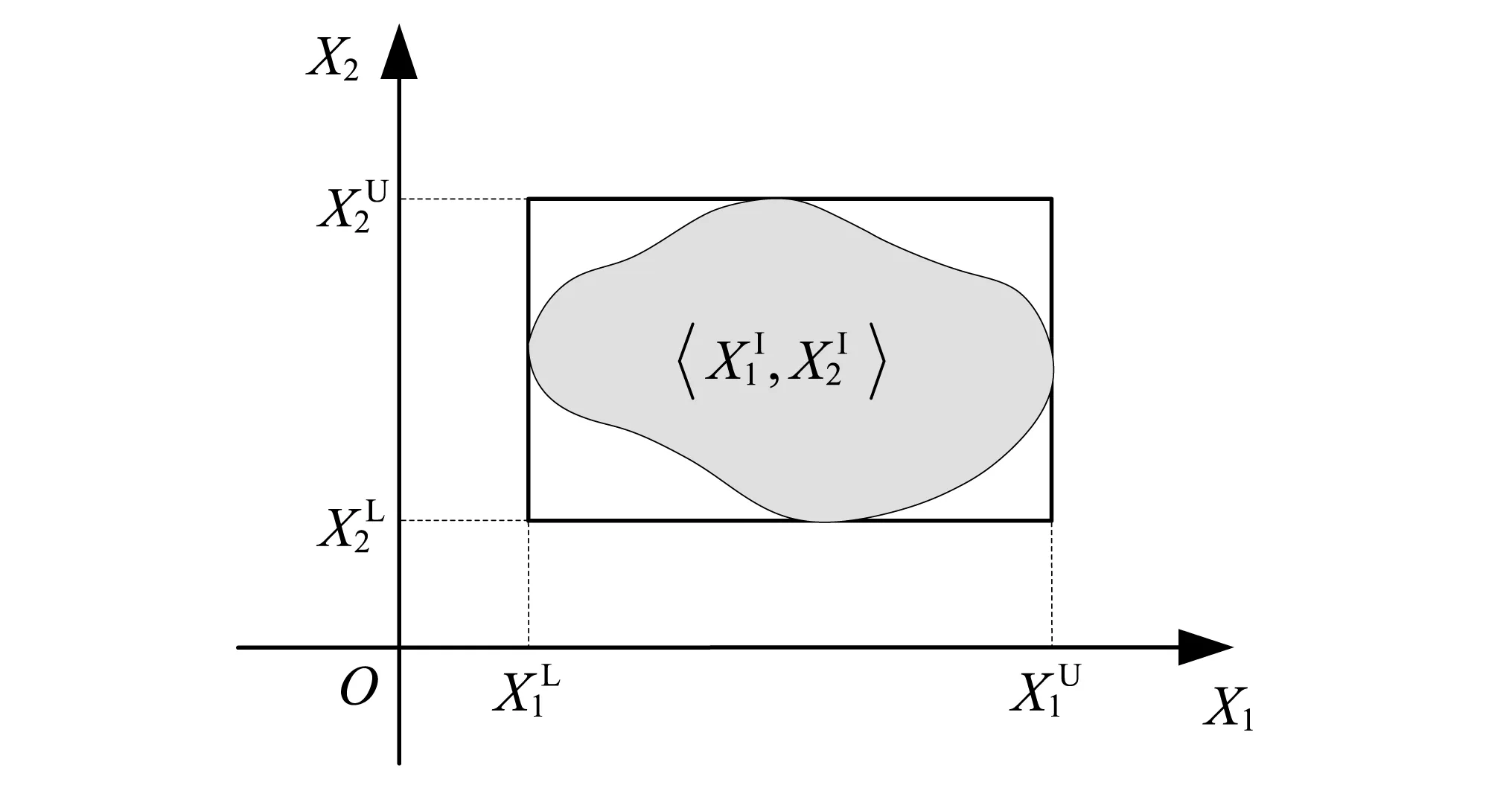
图1 二维有界不确定结构的参数变化区域及其区间模型Fig.1 The variables domain and interval model of a two dimensional uncertain structure

区间模型中，作为区间变量XI的函数，整体刚度和质量矩阵也都是区间矩阵，分别表示为KI和MI。则根据式(2)和式(5)，各阶自然频率以及各自由度之间的频率响应也都在特定的区间范围内变化。接下来的部分主要介绍一种计算有界不确定结构各阶自然频率以及各自由度之间频率响应的模拟方法。

2.1 改进均匀试验设计抽样

均匀设计(Uniform Design, UD)由FANG等[11-12]提出。它是一种试图让设计点均匀分散在试验区域中的空间填充设计方法[13]。UD特别适用于那些模型未知的情况，它既能用在工程试验中，也可以用在数值模拟试验中。UD的试验次数等于其水平数，因此较为省时省力，特别是当不确定变量数较多且变量相关的情况下尤为突出。

UD主要被用来模拟区间模型的输入参数变量。文中使用的均匀设计表由好格子点法生成，通过计算均匀设计表中各组试验点的中心化L2偏差，选取偏差最小的一组试验点模拟不确定参数变量，最小的中心化L2偏差表明该组试验点具有最佳的均匀性。图2(a)和图2(b)分别为2因素、100水平的拉丁超立方抽样点和均匀试验设计抽样点分布示意图，从图2可知，试验设计抽样点的分布明显比拉丁超立方抽样点更加均匀。

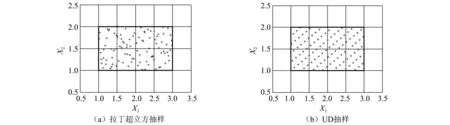
图2 2因素、100水平数试验设计样本示意图Fig.2 Sampling illustrations for experimental designs with 2 factors and 100 levels

UD使样本点更加均匀的填充变量空间，因而可以极大的增加抽样效率。但文中针对有界不确定结构，其变量取值边界处的信息往往会对结构分析的结果产生很大的影响，为此，文章在UD的基础上加以改进，在不增加计算成本的情况下使原本均匀分布的样本点向边界移动，使得更多的样本点分布到变量的取值边界处。改进的原理为

(8)

式中：x为对应样本点的某个变量原始值；ximp为该变量的改进值；xu为该变量取值区间的均值；xr为该变量取值区间的离差。图2(b)中2因素、100水平的UD经改进后样本点分布如图3所示。从图3可知，靠近边界的样本点尤其是靠近边界交角处的样本点明显增多。

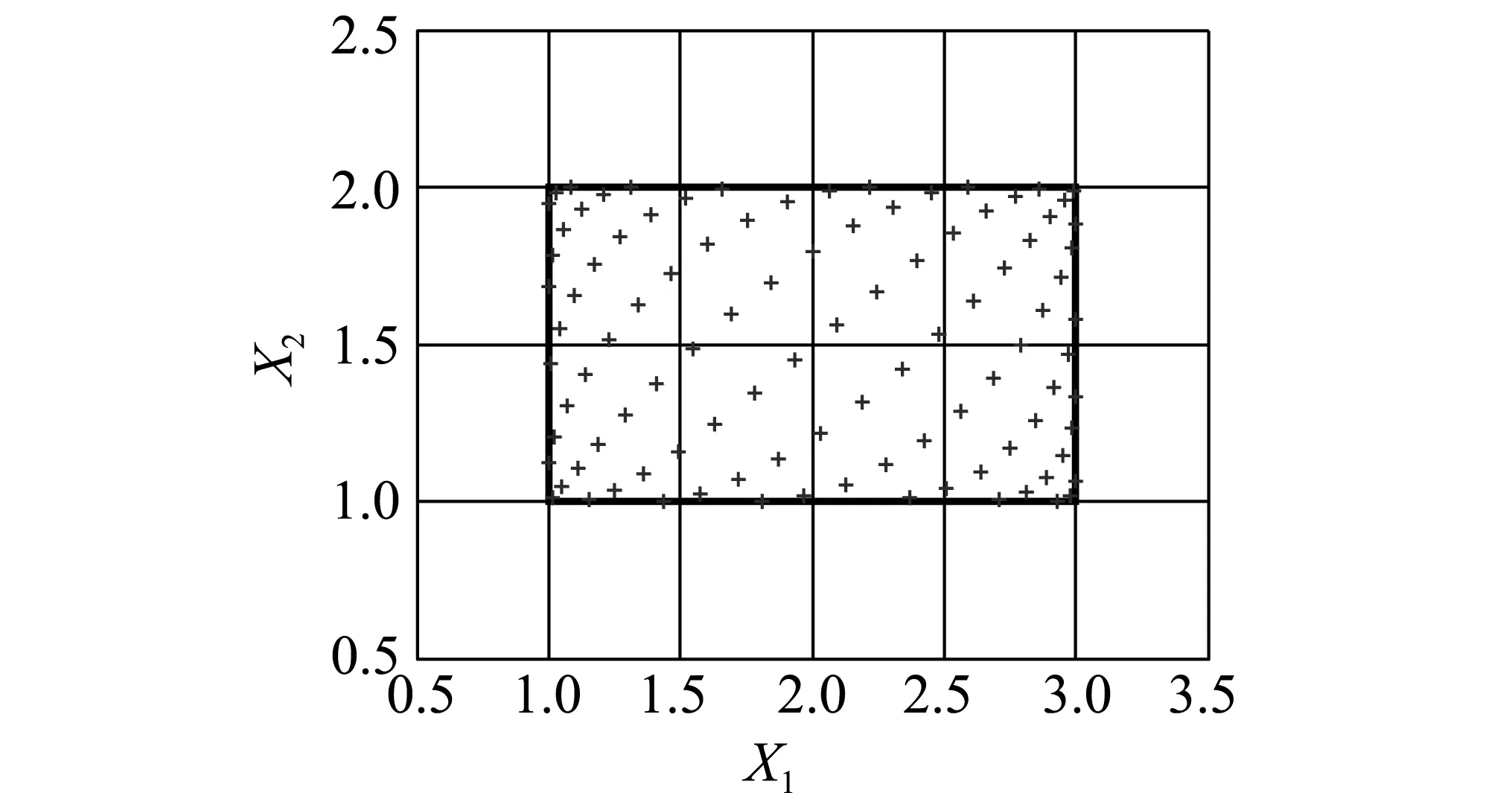
图3 2因素、100水平数改进UD样本示意图Fig.3 Sampling illustrations for improved UD with 2 factors and 100 levels

2.2 频率区间的计算与FRF包络线模拟

频率分析的目的就是确定各阶自然频率的变化区间，而频响分析的目的是确定频率响应曲线变化区域，也即确定FRF包络线。到目前为止，有很多确定频率区间以及FRF包络线的方法被学者提出，其中主要有顶点算法，全局优化算法以及一些基于区间运算的转换算法，等等。上述方法或多或少具有一定的局限性：顶点算法要求自然频率的变化对输入参数变量具有单调性，这样才能保证频率的极值在变量取值区域的某个顶点处取得，在单调性未知的情况下，该算法需要进行2p次的有限元分析，P代表不确定参数的个数。当不确定参数较多时，该方法的计算量会变得很大；全局优化算法的效率取决于初始点的选取和优化程序的选择，该算法容易出现早熟现象而无法得到较为精确的结果，特别是当模型非线性程度较高时，且优化算法收敛迭代的次数直接决定了需要进行有限元分析的次数；由于转化算法以区间运算作为运算基础，考虑到区间运算在变量相关时易出现区间扩张现象，其结果往往偏保守。

考虑到上述方法种种局限性，尝试采用改进的均匀试验设计抽样模拟算法(Improved Uniform Design Sampling Simulation Algorithm，UDS)计算自然频率的变化区间并模拟FRF包络线。图4以流程图形式展示了频率区间和FRF包络线的UDS算法，算法主要分为以下四步：

步骤2 生成区间模型的样本点。用n因素、q水平的改进均匀试验设计抽样，生成样本点，最后选择均匀性最好的一组样本点模拟不确定参数。UD的因素数等于不确定参数的个数，水平数则根据精确度和计算量的折中进行选取。

步骤3 进行确定性的频率和FRF计算。由上一步，生成的q个点分别对应q组确定的参数变量。在这一步当中，依次将q组确定的参数变量带入结构中，计算每组参数对应的各阶自然频率，并计算每组参数对应的FRF值，总共得到q组各阶自然频率和FRF曲线。

步骤4 计算各阶自然频率变化的上下界，并模拟FRF包络线。分别计算q组各阶自然频率中的最大值和最小值，从而得到各阶自然频率变化的上下边界；得到的各FRF曲线共同组成区域的边界线即为不确定结构FRF包络线。

图4 区间模型动力特性分析的UDS方法Fig.4 The flowchart of UDS method for interval dynamic analysis

UDS方法在计算频率区间以及FRF变化区域时有一些优点。该方法由于没有进行区间运算，从而避免了区间扩张的产生；方法可以用在变量较多的模型当中；且既能适用在参数变量变化范围较小的结构中，也能适用在参数变量变化范围较大的结构中。UDS方法由于需要的抽样点数较少，相比较蒙特卡洛模拟方法有较高的计算速率，但较高的计算精度仍然需要生成较多样本点，从而使计算量较大，因此方法还需要在计算精度和计算速率之间作出折中。接下来的内容将着眼于进一步提高UDS方法的计算效率上。

3 基于LS-SVM回归代理模型的模拟方法

前文中提出的UDS方法，其计算量主要集中在对结构的有限元分析上。因而有两种办法可以提高计算效率：①减少计算时间，前文中使用均匀试验设计抽样选取样本点的方法已大大减少了样本点的数量，从而减少了有界不确定结构有限元分析的次数，使计算时间得到了有效的控制；②提高计算精度，UDS算法的精度和计算时间成正比，因此其计算效率不高，文章在接下来的部分试图用少量样本训练得到LS-SVM回归代理模型，进而对代理模型进行随机抽样，从而对结构进行模拟的方法提高计算效率。

3.1 LS-SVM回归代理模型

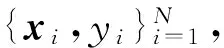
(9)

满足约束条件

yi=ωT·φ(xi)+b+ei,i=1,2,…,N

(10)

式中：ωT·φ(xi)+b为支持向量机模型表达式；ω为权重向量；φ(x)为映射函数；b为偏置量；ei为误差。式(9)中的γ为正规化参数，它代表训练误差最小化和回归估计函数光滑度之间的权衡。则上述回归优化对偶问题的拉格朗日多项式可表示为

(11)

式中，α为拉格朗日乘子，式(11)的最优化条件满足

(12)

消去式(12)中的ω和ei，最终式(12)转换为

(13)

式中：y={y1,y2,…,yN}T; 1N={1,1,…,1}T;α={α1,α2,…,αN}T;Φ=[Φij]为核矩阵，Φij满足如下表达式

Φij=φ(xi)Tφ(xj)=K(xi,xj),

i,j=1,2,…,N

(14)

式中，K:Rdx×Rdx→R为满足Mercer条件[14]的核函数。文中使用径向基核函数K(xi,xj)=exp(-‖xi-xj‖2/σ2)。最终，LS-SVM回归代理模型可表达为如下形式

(15)

3.2 LS-SVM回归的参数选取

选用径向基函数(Radial Basis Function, RBF)作为LS-SVM回归的核函数，其重要参数主要是正规化参数γ和RBF核函数参数σ2，这两个参数的选取会直接影响到LS-SVM回归代理模型的精度。文中参数的选取是通过耦合模拟退火(Coupled Simulated Annealing, CSA)[15]优化算法实现的，算法优化的目标是使LS-SVM回归样本训练的10层交叉验证[16]得到的均方误差(Mean Square Error, MSE)取得最小值。CSA优化算法对初始参数的灵敏度较低，因此具有较好的优化效率，因而能提高总体模拟算法的效率。

3.3 基于LS-SVM回归的模拟方法

考虑变量取值边界对分析结果的影响，使用“2.1”中的改进均匀试验设计抽样方法为LS-SVM回归模型选取训练样本点。得到的样本点分散在整个变量取值区域，并且在区域边界处样本点较多。

通过样本点训练得到LS-SVM回归代理模型之后，就可以用代理模型代替原结构模型对有界不确定结构进行结构动力特性分析，从而提出基于LS-SVM回归的模拟方法(Least Squares Support Vector Machine Regression Based Simulation Algorithm，LSSVRS)。图5以流程形式展示了LSSVRS方法，主要由以下六个步骤组成：

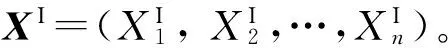
步骤2 生成训练样本点。用改进的均匀试验设计生成样本点，最后选择均匀性最好的一组样本点作为LS-SVM回归的训练样本。

步骤3 计算样本点对应的频率和振动模态。对每个样本点进行确定性的有限元分析，计算每个样本点对应的结构各阶自然频率，并计算各阶频率对应的归一化标准振动模态。

步骤4 训练样本点，得到LS-SVM回归代理模型。别选定各阶自然频率和归一化标准振动模态为目标函数，将样本点进行LS-SVM回归训练，通过优化得到正规化参数γ和RBF核函数参数σ2之后，最终得到回归代理模型。

步骤5 开展确定性的频率计算。首先按照蒙特卡洛模拟法需要的样本数量进行随机抽样；然后依次将每个样本点对应的参数变量带入结构中，计算样本点对应的各阶自然频率以及FRF曲线。

步骤6 计算各阶自然频率变化的上下界并模拟FRF包络线。分别计算各阶自然频率中的最大值和最小值，从而得到各阶自然频率变化的上下边界，并通过模拟FRF曲线，得到不确定结构某两自由度之间FRF变化的范围，即得到FRF包络线。

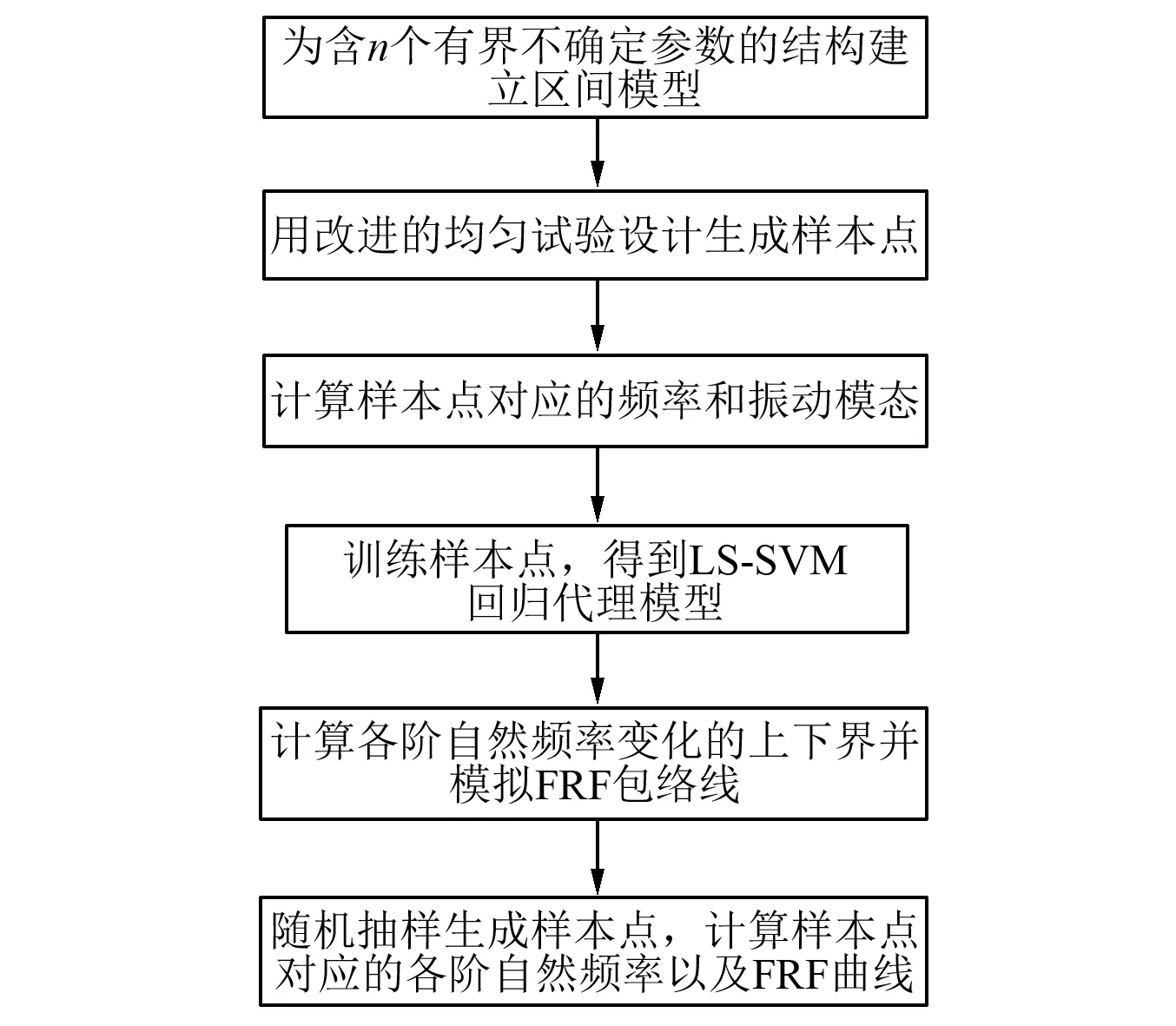
图5 区间模型动力特性分析的LSSVRS方法Fig.5 The flowchart of LSSVRS method for interval dynamic analysis

使用代理模型大大减少了耗时的有限元分析过程的次数，并且在模拟FRF包络线时，代理模型以振动模态为目标函数，因而避开了耗时的频率响应分析过程，从而大大缩短了LSSVRS算法的计算时间。考虑到用代理模型进行结构分析的耗时非常短，因此可以用LSSVRS方法对结构进行动力特性分析，且其效率和精度都高于UDS算法。

4 算 例

4.1 平面桁架结构

图6所示为9根杆的平面桁架结构。已知各杆的横截面积均为2.5×10-3m2，而各杆的弹性模量和密度为有界不确定变量，其中①、③、④、⑥、⑦、⑧号杆的参数取值范围分别为E1=E3=E4=E6=E7=E8∈[180，220]GPa，ρ1=ρ3=ρ4=ρ6=ρ7=ρ8∈[7 760，7 960]kg/m3；②、⑤、⑨号杆的参数取值范围分别为E2=E5=E9∈[190，210]GPa，ρ2=ρ5=ρ9∈[7 810，7 910]kg/m3。

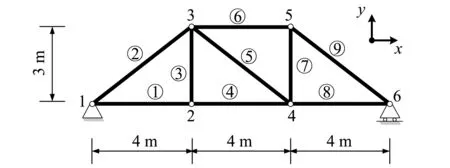
图6 9杆平面桁架结构Fig.6 9 bar plane truss structure

则平面桁架结构前五阶自然频率区间如表1所示。其中由灵敏度单调性判别方法[17]得到的结果是自然频率区间的精确解。分别用UDS算法和LSSVRS算法对不确定变量取10个样本点、40个样本点、100个样本点的平面桁架结构进行计算，得到自然频率区间，并和精确解进行比较，得到分别对应上下边界的相对误差，其中LSSVRS算法对LSSVM回归模型进行了200 000次随机抽样。

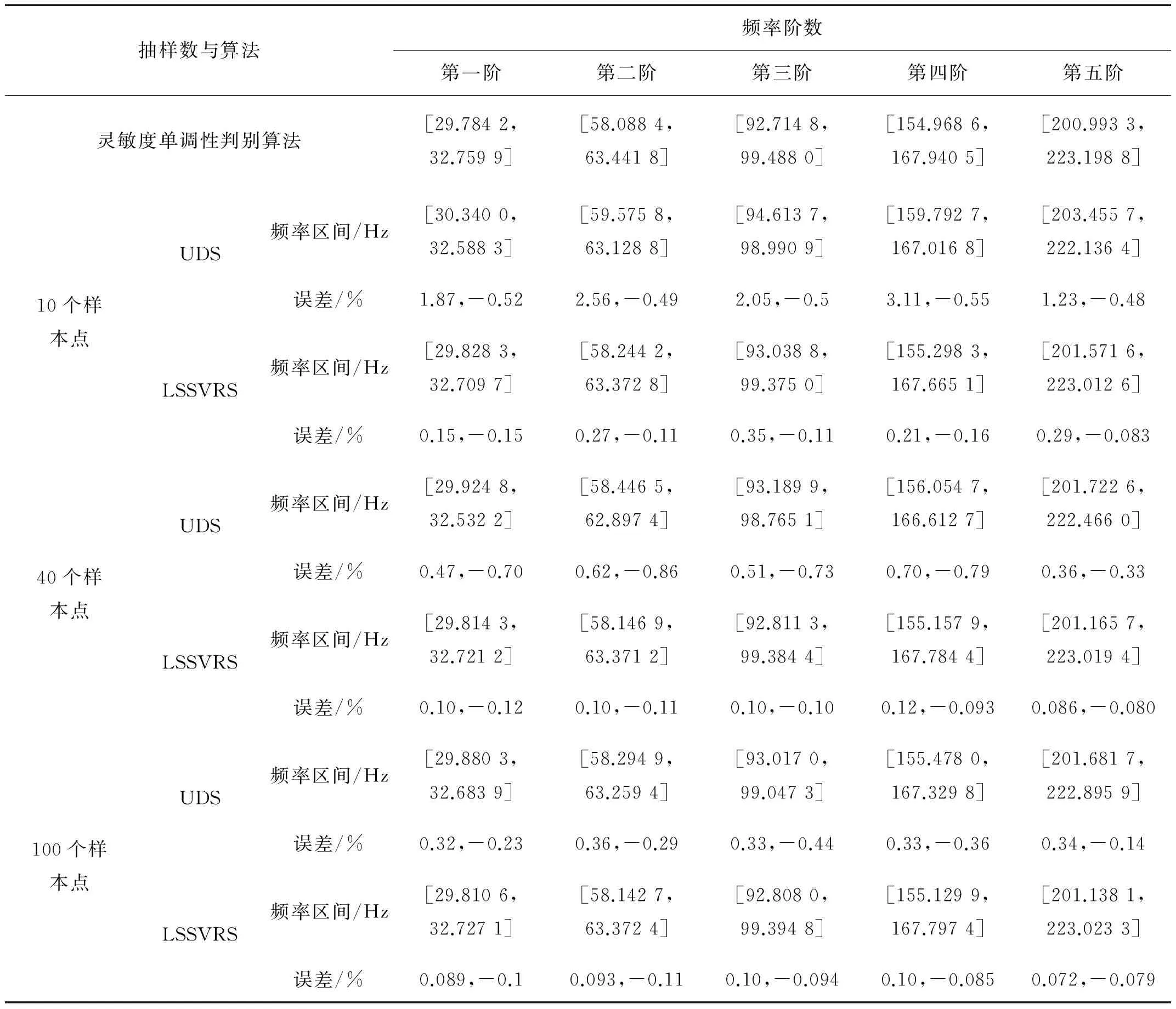
表1 不确定平面桁架结构的自然频率区间

考虑无阻尼的情况，考查输入在节点2的y方向自由度时节点5的y方向自由度的位移FRF包络线。分别用UDS算法和LSSVRS算法对不确定变量取10个样本点、40个样本点、100个样本点的9根杆的平面桁架结构进行FRF分析计算，得到FRF包络线的局部区域如图7所示，其中LSSVRS算法同样对回归模型进行了200 000次抽样。图7中点划线为由UDS得到的FRF包络线，虚线为由LSSVRS算法得到的包络线，实线对应于由灵敏度单调性判别方法求得的最大最小频率，由式(6)可知这两条FRF曲线为所能得到的所有FRF曲线的外边界，因此可视为有界不确定结构FRF包络线的准确值。

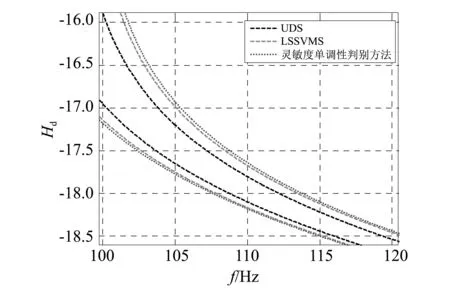
(a)10个样本点

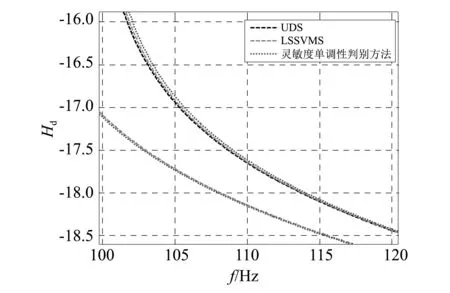
(b)40个样本点

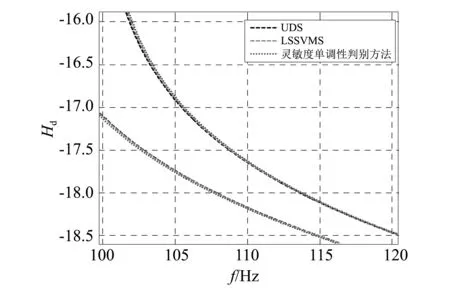
(c)100个样本点图7 9杆平面桁架结构Fig.7 9 bar plane truss structure

4.2 空间刚架结构

图8所示为由12个空间梁构成的空间刚架结构。已知各个梁的横截面积为0.01 m×0.01 m，而各个梁的弹性模量、泊松比和密度为有界不确定变量，其中①、②、③、④号梁的参数取值范围分别为E1=E2=E3=E4∈[200，220]GPa，μ1=μ2=μ3=μ4∈[0.29，0.31]，ρ1=ρ2=ρ3=ρ4∈[7 760，7 960]kg/m3；⑤、⑥、⑦、⑧号梁的参数取值范围分别为E5=E6=E7=E8∈[190，230]Gpa，μ5=μ6=μ7=μ8∈[0.285，0.315]，ρ5=ρ6=ρ7=ρ8∈[7 810，7 910]kg/m3； ⑨、、、号梁的参数取值范围分别为E9=E10=E11=E12∈[195，225]GPa，μ9=μ10=μ11=μ12∈ [0.295， 0.305]，ρ9=ρ10=ρ11=ρ12∈[7 790，7 930]kg/m3。

通过计算得到的空间刚架结构前五阶自然频率区间如表2所示。其中自然频率区间的精确解仍然由灵敏度单调性判别方法得到。依然用两种算法分别对不确定变量取10个样本点、40个样本点、100个样本点的空间刚架结构进行计算，从而得到自然频率区间及其对应上下边界的相对误差，其中LSSVRS算法仍然对回归模型进行了200 000次随机抽样。

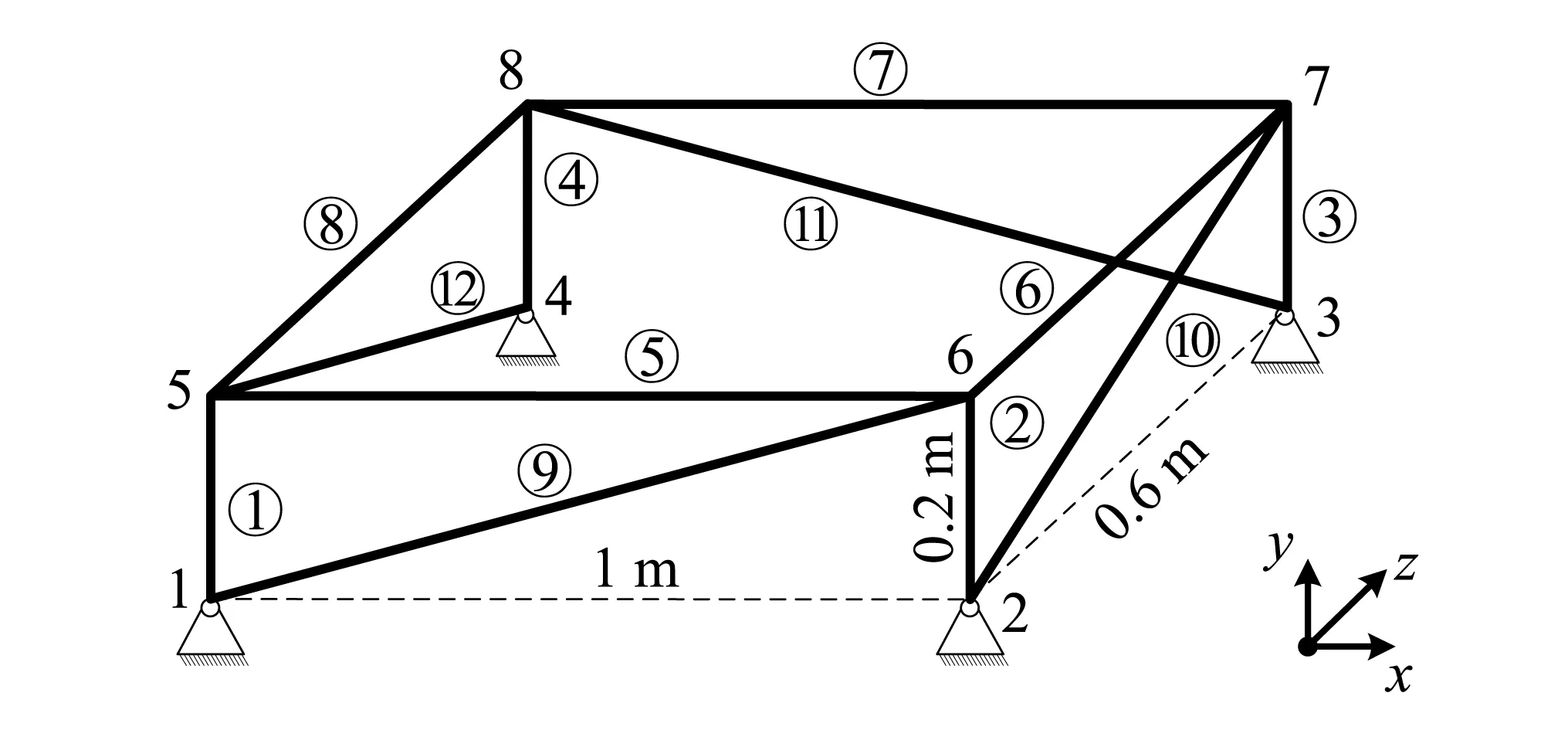
图8 12梁空间刚架结构Fig.8 12 beams space frame structure

仍考虑无阻尼的情况，考查输入在节点5的z方向自由度时节点7的z方向自由度上的位移FRF包络线。对不确定变量分别取10个样本点、40个样本点、100个样本点的空间刚架结构进行FRF分析计算，得到FRF包络线的局部区域如图9所示，其中LSSVRS算法同样对回归模型进行了200 000次抽样。图9中点划线包络线由UDS算法得到，虚线包络线由LSSVRS算法得到，实线包络线对应于由灵敏度单调性判别方法求得的最大最小频率。

用UDS和LSSVRS两种算法计算频率区间，从表1数据可看出，随着样本点的增加，两种算法结果的误差都明显减小，精度显著增加；而表2中数据则显示随着样本点的增加，两种算法精度总体有所增加，但变化并不非常明显，原因在于在样本点较少时，算法精度已经较高。从表1和表2都可以发现，在样本点相同的前提下，LSSVRS算法的误差明显小于UDS算法，因此在计算量基本相同时，LSSVRS算法在计算频率区间时具有更高的计算精度，因此效率更高。

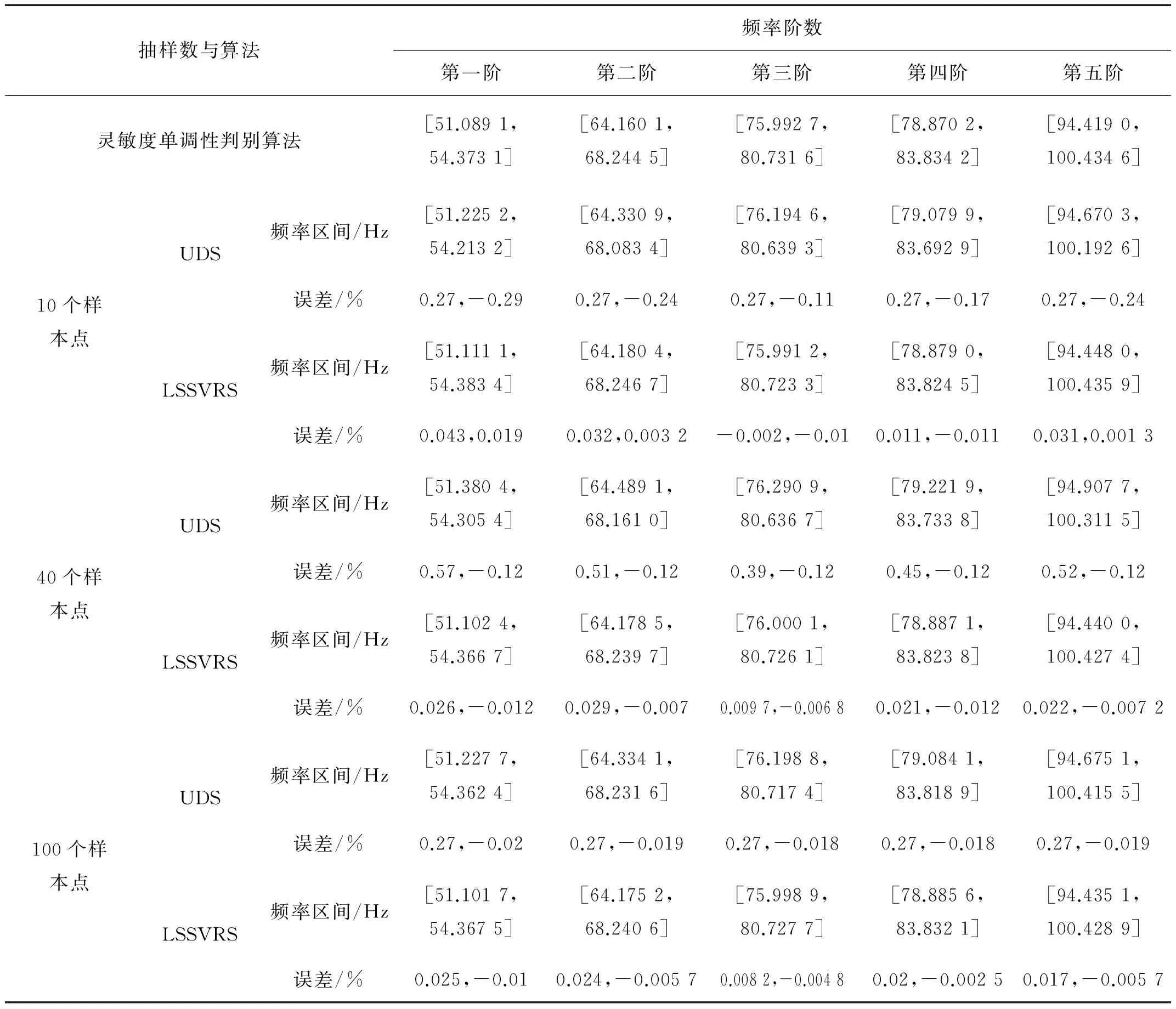
表2 不确定空间刚架结构的自然频率区间

图7和图9分别展示了用两种模拟方法绘制的FRF包络线。其中的实线对应于各自频率区间取到最大最小值时对应的FRF曲线。考虑结构无阻尼的情况，根据式(6)，FRF曲线上靠近某阶自然频率的位置，其幅值趋于无穷或0。则自然频率区间的上边界对应所有FRF曲线最右侧的实线，而下边界对应其左侧的实线，则实线所构成的包络线可视为无阻尼结构的FRF包络线的准确值。从图7和图9可以看出，UDS和LSSVRS两种算法得到的不确定结构FRF包络线都包含在FRF包络线精确范围以内，且随着样本点数量的增加，两种方法的结果都向FRF包络线准确值靠近；同时在计算FRF包络线时，在样本点相同的前提下，LSSVRS算法的精度明显较高，且以用100个样本对9根杆的桁架进行FRF计算为例，UDS算法用时14 min 32 s，而同一台计算机，同样的运算参数设置下，200 000次模拟的LSSVRS算法用时1 min 56 s，且LSSVRS算法结果精度得到了较大提升。这是因为LSSVRS算法避开了耗时的频率响应分析过程，且用代理模型进行结构分析的耗时非常短的缘故。

“4.1”的算例 有4个有界不确定变量，“4.2”的算例有9个有界不确定变量，说明两种算法不仅能够用于变量数较少的不确定结构，也能适用于变量数较多的不确定结构。且两个算例中，当变量取10个样本点时，LSSVRS算法结果的误差就比较小，说明LSSVRS算法在小样本条件下也有较好的性能。

5 结 论

文章将有界不确定结构中的参数变量简化为区间变量，对变量进行区间范围内的改进均匀试验设计抽样，然后在确定结构动力特性分析的有限元法和模态叠加理论基础上，提出了区间频率分析和FRF包络线模拟的UDS算法以及LSSVRS算法。通过两个算例的验证计算发现：

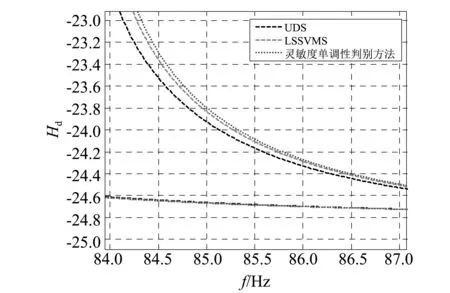
(b)40个样本点

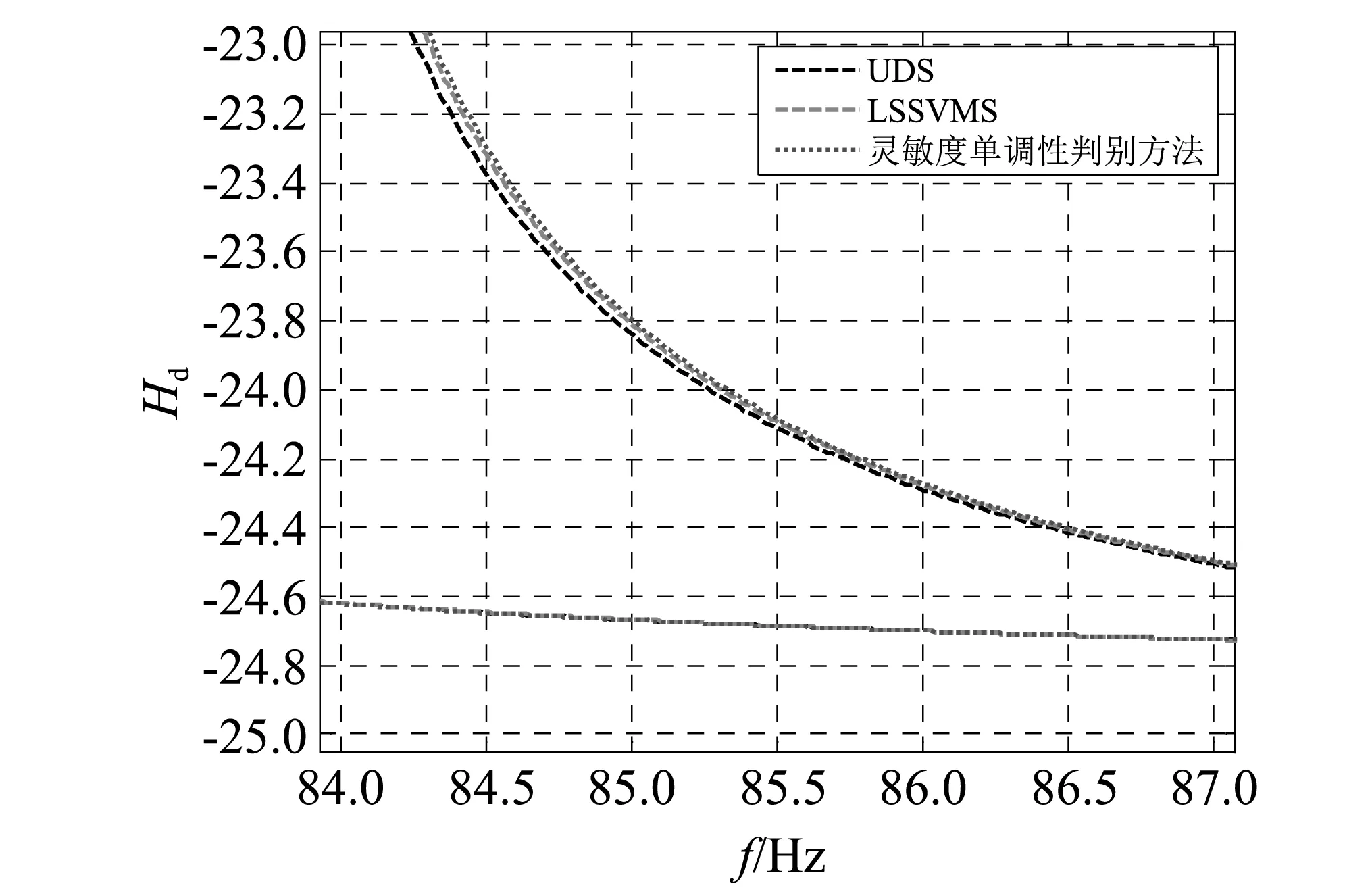
(c)100个样本点图9 12梁空间刚架结构Fig.9 12 beams space frame structure

(1)LSSVRS算法在对有界不确定结构做区间频率分析时，和UDS方法有相近的计算速率，这是因为在样本点相同的情况下两种算法需要进行的有限元分析次数是相等的，但LSSVRS算法计算的精度比UDS算法高；在做FRF包络线计算时，LSSVRS算法的计算速率比UDS方法高很多，且精度也比UDS算法高。

(2)两种算法都有较好的小样本性能，但LSSVRS算法的计算效率、计算精度更高。

(3)两种算法的结果都在区间频率精确解以及FRF包络线准确值的内部，也就是两种算法的结果是从区间和包络线准确值的内部向准确值进行逼近的，说明算法不存在区间扩张的问题。

(4)两种算法同时适用于变量较多和变量较少的有界不确定结构。

[ 1 ] BEN-HAIM Y, ELISHAKOFF I. Convex models of uncertainty in applied mechanics[M]. Amsterdam：Elsevier Science Publisher, 1990.

[ 2 ] 王登刚. 计算具有区间参数结构的固有频率的优化方法[J]. 力学学报，2004,36(3): 364-372. WANG Denggang. Global optimization method for computing frequencies of structures with interval uncertain parameters[J]. Acta Mechanica Sinica, 2004,36(3): 364-372.

[ 3 ] 张建国, 陈建军, 马孝松, 等. 不确定结构动力特征值区间分析的一种算法[J]. 应用力学学报，2006,23(1): 96-100. ZHANG Jianguo, CHEN Jianjun, MA Xiaosong, et al. Method for dynamic eigenvalues interval analysis of uncertain structures[J]. Chinese Journal of Applied Mechanics, 2006,23(1): 96-100.

[ 4 ] 马梁 ,陈塑寰 ,孟广伟. 区间参数有大变化时的结构特征值分析[J]. 吉林大学学报(工学版)，2009,39(1): 98-102. MA Liang, CHEN Suhuan, MENG Guangwei. Eigenvalue analysis of structures with large variations of interval parameters[J]. Journal of Jilin University(Engineering and Technology), 2009,39(1):98-102.

[ 5 ] MANSON G. Calculating frequency response functions for uncertain systems using complex affine analysis[J]. Journal of Sound and Vibration, 2005,288(3):487-521.

[ 6 ] GERSEM H D, MOENS D, DESMET W, et al. Interval and fuzzy dynamic analysis of finite element models with superelements[J]. Computers & Structures, 2007, 85(5/6):304-319.

[ 7 ] MUNCK M D. MOENS D, DESMET W, et al. A response surface based optimisation algorithm for the calculation of fuzzy envelope FRFs of models with uncertain properties[J]. Computers & Structures, 2008, 86(10): 1080-1092.

[ 8 ] YANG Yaowen, CAI Zhenhan, LIU Yu. Interval analysis of dynamic response of structures using Laplace transform[J]. Probabilistic Engineering Mechanics, 2012,29(7):32-39.

[ 9 ] MA Yanhong, LIANG Zhichao, CHEN Meng, et al. Interval analysis of rotor dynamic response with uncertain parameters[J]. Journal of Sound and Vibration, 2013, 332(16):3869-3880.

[10] SOFI A, MUSCOLINO G, ELISHAKOFF I. Natural frequencies of structures with interval parameters[J]. Journal of Sound and Vibration, 2015,347:79-95.

[11] FANG K T. The uniform design: application of number-theoretic methods in experimental design[J]. Acta Mathematicae Applicatae Sinica, 1980, 3(4):363-372.

[12] FANG K T, LIN D K J, WINKER P, et al. Uniform design: theory and application[J]. Technometrics, 2000,42(3): 237-248.

[13] FANG K T, WANG Y. Number-theoretic methods in statistics[M]. London: Chapman and Hall, 1994.

[14] MERCER J. Functions of positive and negative type and their connection with the theory of integral equations[J]. Philosophical Transactions of the Royal Society, 1909, 209: 415-446.

[15] XAVIER DE SOUZA S, SUYKENS J A , VANDEWALLE J, et al. Coupled simulated annealing[J]. IEEE Transactions on Systems, Man and Cybernetics-Part B, 2010,40(2): 320-335.

[16] AN S J, LIU W Q, VENKATESH S. Fast cross-validation algorithms for least squares support vector machine and kernel ridge regression[J]. Pattern Recognition, 2007, 40(8):2154-2162.

[17] MO Yanyu, GUO Shuxiang, CHENG Tang. A vibration reliability analysis method for the uncertain space beam structure[J]. Shock and Vibration, 2016(1):1-14.

Dynamic characteristics analysis method for uncertain-but-bounded structures based on least squares SVM regression

MO Yanyu1, GUO Shuxiang2, TANG Cheng2

(1. Aeronautic and Astronautic Engineering College, Air Force Engineering University, Xi’an 710038, China;2. Science College, Air Force Engineering University, Xi’an 710051, China)

Dynamic properties analysis for uncertain-but-bounded structures was studied. To reach this goal, uncertain-but-bounded parameters were taken as interval variables, but the distributions of the variables were unknown, and then an interval model was built for each uncertain variable. After an improved uniform design sampling for each interval variable, a dynamic analysis simulation method for uncertain structures was proposed based on the deterministic structure’s dynamic properties analysis with the finite element method and the modal superposition theory. Considering the poor efficiency of the proposed method, an improved method was presented. The improved method was based on the least squares support vector machine (SVM) regression in the premise of unchanged number of sampling points, a surrogate model of SVM regression was introduced. The dynamic characteristics of uncertain structures were simulated and analyzed with this surrogate model trained. Finally, two different numerical examples demonstrated the validity of the proposed approach.

uniform design; interval model; frequency analysis; frequency response analysis; support vector machine (SVM) regression

国家自然科学基金(51175510)

2016-04-21 修改稿收到日期： 2016-09-02

莫延彧 男，博士生，1984年生

郭书祥 男，博士生导师，1964年生

O327

A

10.13465/j.cnki.jvs.2017.07.030