考虑弹性振动的高超声速飞行器预设性能控制
赵贺伟, 胡云安, 杨秀霞, 梁 勇
(海军航空工程学院 控制工程系,山东 烟台 264001)
考虑弹性振动的高超声速飞行器预设性能控制
赵贺伟, 胡云安, 杨秀霞, 梁 勇
(海军航空工程学院 控制工程系,山东 烟台 264001)
针对弹性高超声速飞行器纵向短周期系统,提出一种基于预设性能的backstepping控制器设计方法。将弹性模态作为系统的不确定性,利用全局调节动态神经网络进行在线逼近,引入鲁棒项处理神经网络估计误差带来的影响;将预设性能控制与backstepping技术相结合,引入性能函数的概念,利用误差转化函数将原受限系统转化为等价的非受限系统,然后基于Lyapunov理论设计全状态预设性能backstepping控制器,保证了高超声速飞行器纵向短周期系统误差全状态满足预设的瞬态和稳态性能,理论分析证明了系统的稳定性和闭环系统所有信号均有界。仿真分析验证了提出方法的正确性。
弹性;高超声速飞行器;预设性能;神经网络
随着航空和航天技术的逐步成熟,人们将探索的领域延伸到临近空间,作为临近空间飞行器的高超声速飞行器的研究成为了国内外研究的热点领域。高超声速飞行器具有巨大的军事和民用价值,成为世界各大国争先发展的对象。高超声速飞行器飞行速度快、飞行跨度大、飞行环境复杂多变,各种因素导致高超声速飞行器系统具有高度非线性、强耦合、强时变、弹性振动等显著特点,这些特点给高超声速飞行器的控制器设计带来了巨大的挑战。其中针对高度非线性、强耦合等特点采用的控制方法已非常成熟,而机体弹性问题的解决方法还是比较少,且难度相当巨大,成为近几年研究热点问题。机体的弹性形变和振动对高超声速飞行器是非常不利的,而且与飞行器的气动特性和推力系统都会产生耦合效应,所以弹性振动的抑制问题是保证高超声速飞行器稳定飞行的关键问题。
目前,针对弹性高超声速飞行器控制器的设计出现了大量的相关文献,鲁棒自适应控制方法[1]、神经网络自适应方法[2-3],结构动力学的线性变参数控制方法[4]、这些文献都对高超声速飞行器的弹性振动模态进行了研究;ADAMI等[5-9]利用自适应控制、非线性鲁棒自适应控制等方法对弹性高超声速飞行器进行了研究,但是这些文献都是将六个弹性模态作为系统的状态量,大大增加了系统的维数,从而导致控制器的设计异常困难。
上述这些方法从不同的角度对高超声速的弹性问题进行了研究,但是它们共同的问题在于将六个弹性模态作为系统状态变量的一部分,控制系统设计的难度巨大,而且结构非常复杂,在实际工程中不易实现。同时,上述文献在控制系统设计中只考虑了系统的稳态性能,保证了系统的稳态误差收敛到有界区域,而没有考虑和兼顾系统的瞬态性能(超调量和调节时间等)。预设性能控制是由BECHLIOULIS等[10]首次提出的一种新颖的控制方法,这种控制方法可以兼顾系统的瞬态性能和稳态性能。
针对弹性高超声速飞行器纵向运动模型,将动力学模型中的弹性模态作为系统的不确定性,采用动态神经网络进行逼近,并将预设性能控制与backstepping控制方法相结合,设计了弹性高超声速飞行器纵向姿态控制器。
1 系统描述与预备知识
1.1 系统描述
本文将文献[11]提出的弹性高超声速飞行器纵向运动模型作为研究对象,即
纵向运动模型进行分析,其中高度h和速度v为慢变量,攻角α和俯仰角速度q为快变量,因此纵向运动可以分为内环和外环两个子系统,内环子系统为纵向运动的短周期系统,外环子系统为纵向运动的长周期系统,内环和外环可分别设计控制器,为了体现研究的针对性,本文仅研究内环子系统控制器设计问题,因此只考虑纵向模型中的短周期模型,即
(1)
(2)
(3)
式中:v为飞行器的飞行速度;h为飞行器的飞行高度;T为发动机推力;α为攻角;g为重力常数;γ为航迹倾斜角;m为飞行器质量;L为升力;D为阻力;q为俯仰角速度;Iq为转动惯量;M为俯仰力矩;ψ1、ψ2为耦合系数;ηi为第i阶弹性模态;ki=1+ψi/Iq;ξi为第i阶弹性模态ηi的阻尼系数;ωi为第i阶弹性模态ηi的自然频率;Ni为第i阶广义力。系统的输入量为升降舵偏角δe。系统中的力和力矩表达式为
(4)
(5)
(6)
(7)
(8)
(9)
CM,δe(δe)=ceδe
(10)
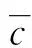
设定控制目标如下:
1) 根据给定的期望指令信号αd,设计backstepping控制器,保证输出信号α能够跟踪期望指令信号αd的同时,闭环系统中的所有信号有界;
2) 输出误差e(t)=α-αd满足预先设定的稳态和瞬态性能。
作如下假设:
假设1期望指令信号及其各阶导数均为已知,并连续有界。
假设2初始误差|e(0)|=|α(0)-αd(0)|有界,且上界为已知常数。
1.2 性能函数
定义1连续函数λ(t):R+→R+为性能函数,其满足下列条件
1)λ(t)为正且严格递减;

为实现控制目标2,选取如下不等式
-κλ(t)
(11)
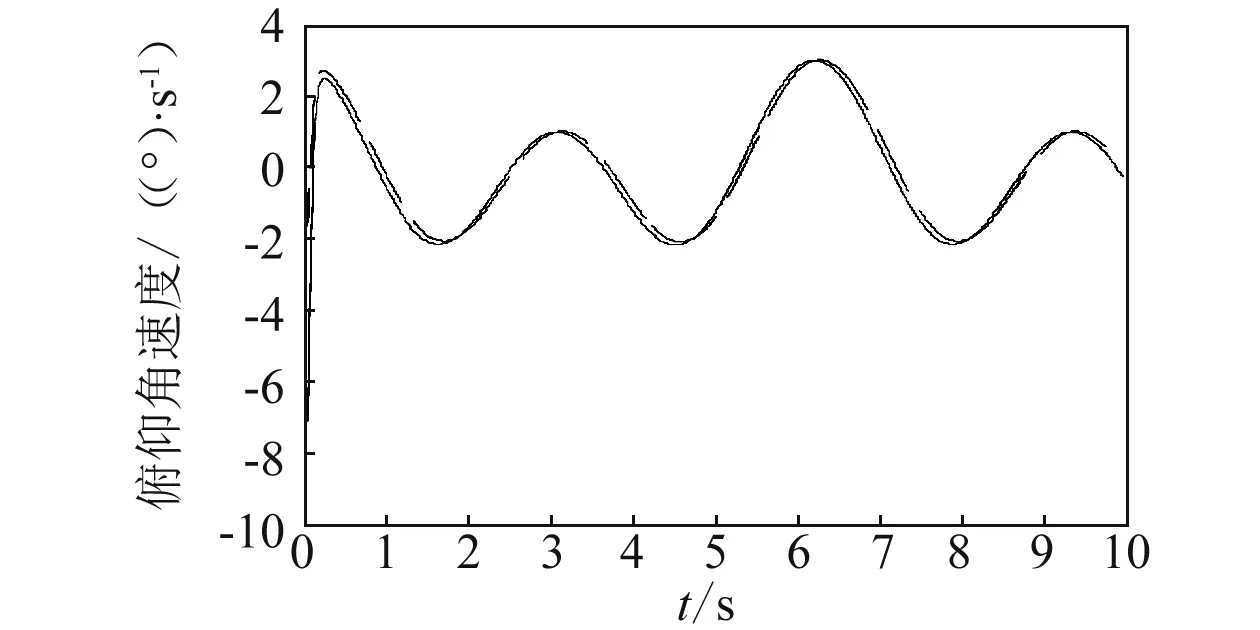
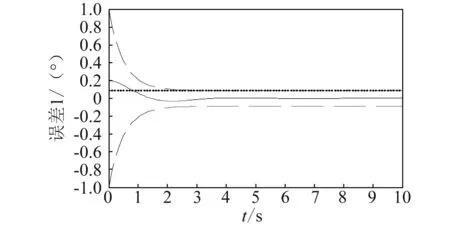
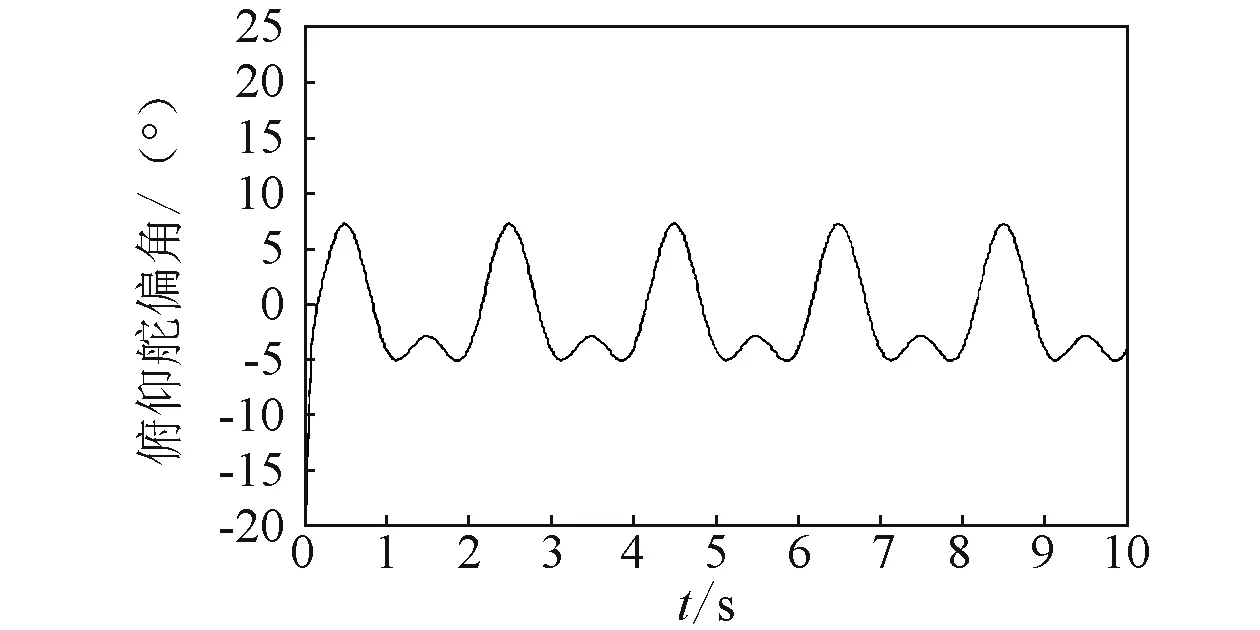
-λ(t) (12) 式中:t∈[0,∞);κ∈[0,1]。 将性能函数选取为 λ(t)=(λ0-λ∞)e-ξt+λ∞ (13) 式中:λ0,λ∞,ξ>0为预先设定的常数,λ∞为预先设定的稳态误差的上限,跟踪误差e(t)的收敛速度的下界等于λ(t)的衰减速度,并保证e(t)的最大超调量不大于κλ0。综上所述,通过选择合适的性能函数λ(t)以及常数κ,则可以实现对跟踪误差的稳态性能和瞬态性能进行限制,可用图1来说明。 (a)式(11)的情况 (b)式(12)的情况图1 性能函数与跟踪误差的关系Fig.1 The relationship of performance function and tracking error 1.3 误差转化 在控制系统设计过程中,不等式约束式(11)、式(12)处理的难度很大,所以需要将其转化为等式约束,具体转化过程为 定义跟踪误差为 e(t)=λ(t)G(ε) (14) 式中:ε为转化误差;G(ε)为误差转化函数,且满足如下性质 1) 误差转化函数G(ε)是光滑的,并且严格递增; 2)G(ε)满足如下不等式 3)G(ε)满足如下等式 根据前述定义,λ(t)>0,当e(0)>0时,则 -κλ(t)<λ(t)G(ε)<λ(t) 根据式(14)可知 -κλ(t) 同理,当时e(0)<0,则 -λ(t) 根据误差转化函数的性质,进一步将误差转化函数进行逆变换 式中,P=G-1。 如果ε(t)∈∞,t∈[0,∞),可得式(11)、式(12)成立。同时,根据性能函数严格递减的性质可以判断跟踪误差终将被限制在如下区域 Ω={e∈R∶|e(t)|≤λ∞} 注1:为避免ε(0)→∞,当e(0)=0时,κ不能设定为0。 注2:根据假设2,选择λ(0)>|e(0)|。 引理1[12]对任意的常数τ>0和变量B∈R,下式成立 定义集合Θ{ε||ε|<0.881 4τ},对于任意的ε∉Θ,下列不等式成立 [1-2 tanh2(ε/τ)]<0 1.4 全局调节动态神经网络 函数矢量Δf:Ω→Rr,Ω为Rn的一个紧子集,对于任意χ=[χ1,χ2,…,χr]T>0,总存在一个最优高斯基函数矢量φ*:Rn→Rl和一个最优权重矩阵W*∈Rl×r使得 Δf=W*Tφ*+χ 其中, 假设3忽略升降舵偏角δe对升力产生的影响。 根据假设3对系统式进行整理可得 (15) (16) 其中, (17) (18) (19) (20) 式中,Δ为弹性模态项,将其作为系统的不确定性来处理,并采用全局调节动态神经网络进行在线逼近。 步骤1定义误差状态e1=α-αd,αd为α的期望指令信号,同时定义误差转化函数e1=λG(ε1),e1和ε1的导数分别为 (21) (22) 定义误差状态e2=q-qd,其中qd为q的期望指令信号。对式(22)进行调整可得 (23) 定义Lyapunov函数为如下形式 (24) 对式(24)求时间的导数,可得 (25) 设计虚拟控制律为 (26) 式(26)中k1>0为设计参数, 将式(26)代入式(25),可得 (27) 步骤2定义误差转化函数e2=λG(ε2),可以得到e2、ε2的导数为 (28) (29) 式(29)中的不确定项Δ利用全局调节动态神经网络进行在线逼近,即 Δ=W*Tφ*+χ (30) 式中: φ*= (31) 其中残留项du的上界为 式中,各项符号(下文同)及证明过程参考文献[14]。 定义Lyapunov函数为如下形式 (33) 将式(33)对时间求导,可得 (34) 将式(29)代入式(34),整理可得 (35) 设计实际的控制律为 (36) 式中:k2>0为设计参数;r为引入的鲁棒项。 将式(27)、式(36)代入式(35),整理可得 (37) 进一步整理式(37)可得 (38) 由式(38)可知 (39) 进一步整理可得 (40) 根据引理1可知,当|ε2|≥0.881 4τ2时, (41) 将不等式(41)代入式(40),可得 (42) 将式(32)代入式(42),可得 (43) 设计自适应调节律如下 (44) (45) (46) 将式(44)~式(46)代入式(43) (47) 考虑到如下不等式 式(47)可以变换为 (48) 根据du的上界可知 (49) 设计鲁棒项为 (50) 式中,z为设计的正常数。 再根据不等式 可将式(49)进一步整理为 (51) 进一步整理式(51)得 (52) 式中, 根据上述理论分析可知,闭环系统所有信号均有界且收敛到系统原点的一个领域内。 定理1针对弹性高超声速飞行器纵向短周期模型,在假设1~假设3条件下,采用控制律式(36),同时在鲁棒项式(50)的作用下,全局调节动态神经网络各参量自适应调节律为式(44)~ 式(46),系统状态跟踪误差满足预先设定的瞬态和稳态性能的要求,且闭环系统所有信号均有界。 仿真中的气动力和力矩系数的标称值摄动+20%,如表1所示。 表1 气动力和力矩系数 图2为攻角跟踪曲线,实线为期望命令信号,虚线为实际输出的攻角曲线,可以看出实际输出的攻角可以很好地跟踪期望指令信号;图3为俯仰角速度跟踪曲线,实线为期望俯仰角速度跟踪信号,虚线为实际俯仰角速度,可以看出实际的俯仰角速度可以很好地跟踪期望的俯仰角速度。通过图2、图3可知,在考虑机体弹性振动影响的情况下,即使气动力和力矩系数摄动+20%后,本文设计的控制器仍可以保证控制目标的实现。 图4为攻角跟踪误差曲线和预设性能曲线,可以看出误差曲线满足预先设定的瞬态和稳态性能要求;图5为俯仰角速度跟踪误差曲线和预设性能曲线,可以看出跟踪误差满足预先设定的瞬态和稳态性能;通过图4、图5可知,可以保证跟踪误差的瞬态性能和稳态性能的要求,通过仿真曲线可以看出,通过预设性能的设计可以使跟踪误差限定在需要的范围内,这对于高超声速飞行器在巡航段实现精细姿态控制是重要的保证。同时,高超声速飞行器在过渡飞行阶段需要快速跟踪期望攻角,本文的预设性能控制通过预设性能的设计可以保证飞行器攻角跟踪误差的调节时间和超调量等瞬态性能满足过渡段飞行要求。通过仿真结果可以得知,两个跟踪误差都能够实现预设性能,即实现了全状态具有预设性能,而一般的预设性能控制只能保证输出状态跟踪误差的预设性能要求。 图6为俯仰舵偏角曲线,可见曲线平滑有界。通过仿真结果可以说明控制器设计的有效性。 图2 攻角仿真结果Fig.2 Simulation result of angle of attack 图3 俯仰角速度仿真结果Fig.3 Simulation result of rate of pitch 图4 e1及预设性能曲线Fig.4 The curve of e1 and prescribed performance 图5 e2及预设性能曲线Fig.5 The curve of e2 and prescribed performance 图6 俯仰舵偏角仿真结果Fig.6 Simulation result of elevator deflection (1) 本文提出的预设性能控制方法,不仅仅是输出满足预设性能的要求,而是系统的全状态都满足预设性能的要求,这种设计方法优于一般的预设性能控制。 (2) 文中通过“引理1”的使用,巧妙地抵消了预设性能控制带来的需要特殊处理的项,同时双曲函数能够增强系统的鲁棒性。 (3) 本文利用全局调节动态神经网络在线逼近系统的弹性振动模态,从将解决弹性振动模态对系统的影响。全局调节动态神经网络是利用自适应调节律对RBF神经网络的最优权值、中心点和影响范围进行在线调节,这大大增强了RBF神经网络的逼近能力和适应性。 (4) 本文提出的预设性能控制使攻角的稳态误差限定在一定范围之内,又使跟踪误差的调节时间和超调量满足预设性能要求,这对于实现高超声速飞行器巡航段的精细姿态控制和实现在过渡段的攻角快速跟踪控制提供了一种可行的思路。 [ 1 ] SIGTHORSSON D O, JANKOVSKY P, SERRANI A, et al. Robust linear output feedback control of an airbreathing hypersonic vehicle[J]. Journal of Guidance Control ﹠Dynamics, 2008, 31(4):1052-1066. [ 2 ] XU H J, MIRMIRANI M, IOANNOU P A. Robust neural adaptive control of a hypersonic aircrafot[R]. AIAA-2003-5641, 2003. [ 3 ] WALLNER E M, WELL K H. Nonlinear flight control design for the X-38 using CMAC neural networkso[R]. AIAA-2001-4042, 2001. [ 4 ] KUIPERS M, MIRMIRANI M, IOANNOU P, et al. Adaptive control of an aeroelastic airbreathing hypersonic cruise vehicleo[R]. AIAA-2007-6326,2007. [ 5 ] ADAMI T A, ZHU J J.Control of a flexible hypersonic scramjet vehicle using a differential algebraic approach[R]. AIAA 2008-7464, 2008. [ 6 ] FIORENTINI L, SERRANI A, BOLENDER M A,et al. Nonlinear robust/adaptive controller design for an air-breathing hypersonic vehicle model[R]. AIAA 2007-6329, 2007. [ 7 ] JANKOVSKY P, SIGTHORSSON D O, SERRANI A, et al. Output feedback control and sensor placement for a hypersonic vehicle model[R]. AIAA 2007-6327, 2007. [ 8 ] KUIPERS M, MIRMIRANI M, IOANNOU P, et al. Adaptive control of an aeroelastic airbreathing hypersonic cruise vehicle[R]. AIAA 2007-6326, 2007. [ 9 ] HEEG J, GILBERT M G, POTOTZKY A S. Active control of aerothermoelastic effects for a conceptual hypersonic cruise vehicle[R]. AIAA 2007-3337, 1990. [10] BECHLIOULIS C P,ROVITHAKIS G A. Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances[C]∥16th Mediterranean Conference on Control & Automation(MED). America: Research Gate,2008:1035-1040. [11] PARKER J T, BOLENDER M A, DOMAN D B. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance Control & Dynamics, 2007, 30(3): 856-868. [12] LEVANT J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance Control & Dynamics, 2007, 30(3): 856-869. [13] 胡云安,晋玉强,张友安,等.基于神经网络的严反馈块非线性系统的鲁棒控制[J].控制与决策,2004,19(7):808-812. HU Yun’an, JIN Yuqiang, ZHANG Youan, et al. NN-based robust control for strict-feedback block nonlinear systems[J]. Control and Decision, 2004, 19(7):808-812. [14] 晋玉强.导弹非线性自适应控制系统设计[D].烟台:海军航空工程学院,2003. Prescribed performance control for a hypersonic vehicle considering elastic vibration ZHAO Hewei,HU Yun’an,YANG Xiuxia,LIANG Yong (Department of Control Engineering, Naval Aeronautical Engineering Institute, Yantai 264001, China) Aiming at the longitudinal dynamic model of an elastic hypersonic vehicle, the short period subsystem controller ws designed using prescribed performance control and the backstepping technique. The elastic modes were taken as the uncertainties of the system, the online approaching was conducted using the fully tuned dynamic neural network and the influences of estimation errors of the neural network were dealed with by introducing the robust term. The prescribed performance control was combined with the backstepping technique, the performance function and the error conversion function were introduced to convert the original ‘constrained’ system into an equivalent ‘unconstrained’ one. The fully states prescribed performance backstepping controller was designed based on Lyapunov theory, it was proved that the system is stable and all the signals are bounded according to the theoretical analysis; all error states of the longitudinal short period subsystem of the typersonic vehicle satisfy the prescribed transient state and steady state performances. The simulation results demonstrated the correctness of the proposed method. elasticity; hypersonic vehicle; prescribed performance; neural network 航空科学基金(20135584010;20140184001);中国博士后基金(2015M572693) 2016-07-28 修改稿收到日期: 2016-08-29 赵贺伟 男,博士生,讲师,1985年生 胡云安 男,博士,教授,1966年生 TH212 A 10.13465/j.cnki.jvs.2017.07.036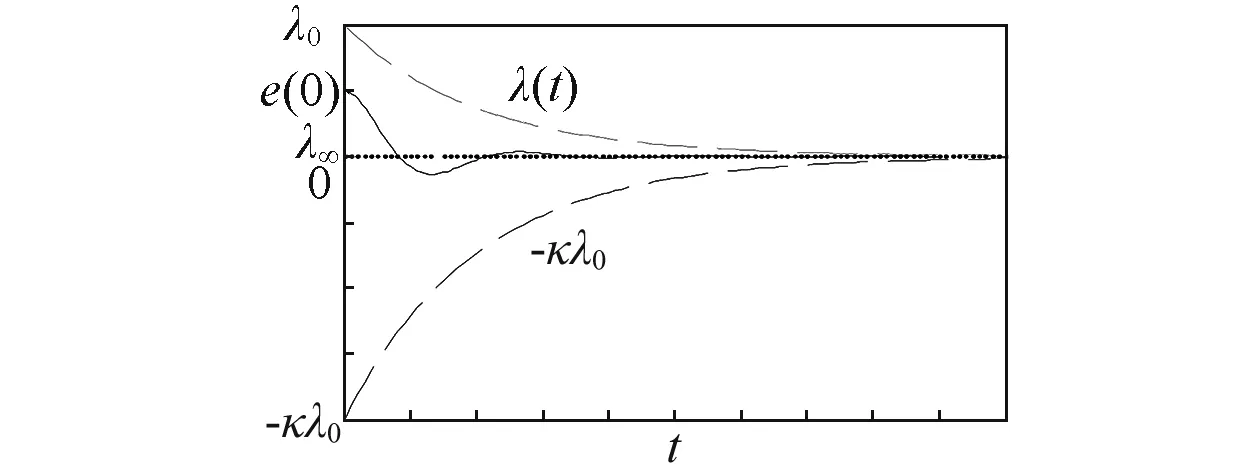

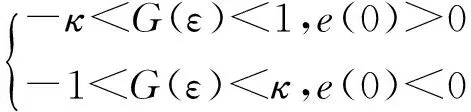



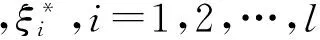
2 预设性能backstepping控制器设计


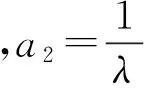
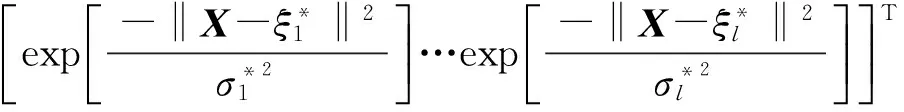
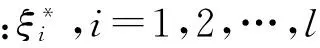

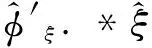





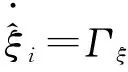
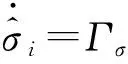


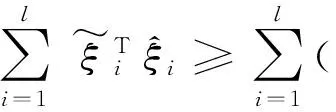

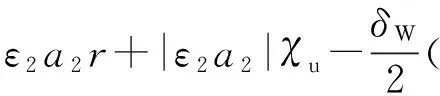
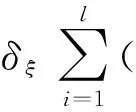



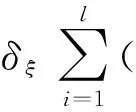

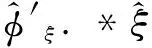
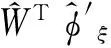
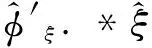



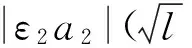
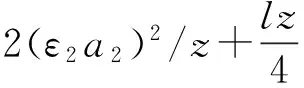
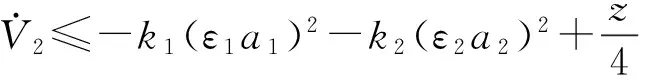
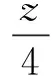
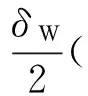
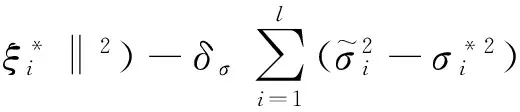
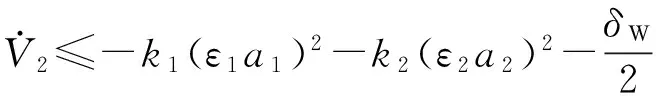

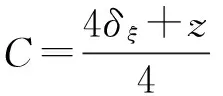
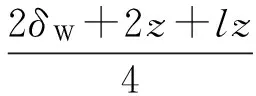
3 仿真分析

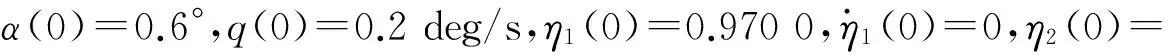


4 结 论

