大跨度悬索桥主引桥碰撞效应振动台试验及数值研究

闫聚考， 李建中， 彭天波， 王军文

(1.石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室，石家庄 050043；2.同济大学 土木工程防灾国家重点实验室，上海 200092；3. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043)

大跨度悬索桥主引桥碰撞效应振动台试验及数值研究

闫聚考1，2， 李建中2， 彭天波2， 王军文3

(1.石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室，石家庄 050043；2.同济大学 土木工程防灾国家重点实验室，上海 200092；3. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043)

为了研究大跨多塔连跨悬桥与引桥间的碰撞效应，以泰州长江公路大桥为背景，设计并制作1/40缩尺比例模型，进行了全桥振动台模型试验。主桥采用中塔与主梁间无连接的纵向约束结构体系，边跨梁每幅采用2个固定支座和4个聚四氟乙烯滑板支座，初始伸缩缝间隙为3 mm，试验分别测试了3条地震波下主引桥间的碰撞响应。振动台试验表明，主桥与引桥相互靠近运动时，主引桥间的碰撞会减小引桥梁位移及固定墩内力的需求；当主桥追逐引桥运动时，主引桥间的碰撞会增大引桥梁位移及内力的需求。数值模拟结果表明：采用SAP2000商业软件组合Kelvin单元，接触刚度取引桥梁轴向刚度的0.2倍时，能较好的模拟试验结果；接触刚度取值可为相似桥梁碰撞效应模拟提供试验参考。

大跨悬索桥；振动台试验；碰撞效应；行波效应；接触刚度

地面上相邻的桥跨结构由于其动力特性存在差异以及地震动输入的空间变化特性，当地震发生时将引起相邻桥跨间的不同步振动，桥跨间预留的间隙不能满足彼此的相对位移时就会发生相互碰撞。然而，在地震中一旦相邻梁体发生碰撞，通常会带来局部的梁体碰撞损伤，同时碰撞对桥梁结构的抗震性能产生影响，巨大的碰撞力会导致支座的失效，伸缩缝两侧过大的相对位移也会导致更为严重的落梁震害。

在1976年唐山大地震中，滦河大桥的落梁破坏曾引起了桥梁抗震工作者们的注意，他们以各种可能原因对震害现象进行了解释，在不同程度上都提到了碰撞作用[1]。在1971年的圣费尔南多(San Fernando)地震中发现，上部结构与桥台间的碰撞是一座座式桥台公路桥破坏的原因[2]。在1989年美国洛马·普里埃塔(Loma Prieta)地震中，由于设计低估了相邻桥跨间的相对位移，预留的支承面太窄，致使旧金山-奥克兰海湾大桥引桥的一跨落梁[3]。在1994年的北岭(Northridge)地震中，位于震中附近的内环5号线与14号洲际公路连接段的几座桥梁的伸缩缝和桥台处都发生了严重的碰撞破坏[4]。在1995年日本阪神地震中，西宫港大桥(主跨252 m的钢系杆拱桥)第一跨引桥落梁的原因主要是主桥和引桥间的相对位移过大，桥墩的支承面太窄，而支座、连接限位构件又失效[5]。

国内外学者已对桥梁结构碰撞问题，在数值模拟及试验方面进行很多研究。目前，对桥梁地震碰撞作用模拟方法有恢复系数法和接触单元法两类。恢复系数法是一种经典的力学分析方法，它运用动量守恒定律以及恢复系数确定两相邻桥梁发生碰撞后的速度。恢复系数法可以处理两个刚体间的碰撞问题，它具有物理概念清楚、算法简单的优点；但恢复系数和碰撞接触时间要事先给定，不适合于碰撞时间持续较长的情况，且不易与商业软件相结合，因此限制了其应用范围。接触单元法是在两相邻跨桥梁之间设置一个接触单元，碰撞发生时接触单元就会被激活。接触单元有时用刚度很大的线弹性弹簧模拟以避免相邻节段碰撞时的材料重叠，有时采用弹簧并联阻尼器来模拟，用阻尼器模拟碰撞过程中能量的耗散。接触单元模型有线性弹簧模型[6]、Kelvin模型[7]、Hertz模型[8]、Hertz-damp模型[9]等几种。为了研究桥面板之间的任意碰撞，ZHU等[10]发展了一种三维接触摩擦模型，虽然这种模型能有效模拟相邻梁体间的任意碰撞，也可以在动力分析常用的数值积分方法中实现，但其搜索算法相当复杂，寻找接触对需要耗费大量机时，故在一定程度上制约了这种方法的发展应用。

接触单元计算的精度取决于碰撞单元刚度、恢复系数等关键参数。但目前接触单元中的碰撞刚度如何计算取值还不明确，通常为了防止碰撞体之间发生侵入现象，在碰撞模拟中需要设定较大的碰撞刚度，但过大的碰撞刚度不仅会带来数值计算的稳定性问题，分析结果中还会出现失真的巨大撞击力。在以往的研究中，众多的学者将 Kelvin 模型的碰撞刚度近似地取值为碰撞结构的轴向刚度[11]。王东升等[12]基于实测的邻梁碰撞强震记录近似估计得到 Kelvin 模型中碰撞刚度取值为 0.31～0.56倍的较短主梁的轴向刚度。李忠献等[13]结合 Hertz 碰撞模型推导了Kelvin 模型中碰撞刚度的计算表达式，但其刚度的计算结果有赖于 Hertz 模型碰撞刚度的取值。现有的研究已表明碰撞刚度的取值对结构地震碰撞反应分析结果的影响很大，不同的取值甚至可以得到截然不同的碰撞模拟结果[14]，因此如何合理地确定碰撞刚度具有非常重要的意义。

尽管已有很多学者对地震中的结构碰撞现象进行了理论分析与数值计算研究，但对碰撞效应进行试验研究的工作还很少。VAN MIER 等[15]进行了防坡堤混凝土构件间的碰撞试验，考虑了三种不同的接触表面形状(球形、圆锥形、截锥形)和两种碰撞接近速度(0.5 m/s 和 2.5 m/s)。试验结果表明：撞击力时程曲线受接触面几何形状及接触刚度的影响很大。为了确定碰撞恢复系数及碰撞刚度的合理取值，JANKOWSKI[16]进行了一系列不同材料小尺寸的球体跌落试验，考虑的材料包括钢材、混凝土、木材和陶瓷。试验结果表明：碰撞恢复系数随着接近速度的增加而减小；接触刚度与接近速度无关，但随着质量的增加略有增大。 针对三跨简支钢梁进行了振动台模型试验，验证了三维接触单元模拟碰撞效应的准确性，并验证了防撞措施的防撞效果。郭安薪等[17]针对两跨简支梁，进行了缩尺比1∶20的振动台模型试验，试验研究了MR阻尼器及SMA装置减小碰撞效应的效果。李忠献等[18]采用一两跨缩尺隔震梁桥模型对其地震碰撞反应进行了振动台试验研究。试验结果表明：采用等效 Kelvin模型可以较为准确地模拟碰撞反应的最大撞击力峰值及主梁位移时程；将磁流变阻尼器安装在邻跨之间可以减小邻跨相对位移，且对墩顶位移不会产生明显影响；增大间隙和减小邻跨动力特性差异可减小碰撞反应；支座特性对碰撞反应有显著影响。

综上所述，目前国内外学者对小跨径、小结构物之间的碰撞效应进行了大量研究[19]，但对于大跨度桥梁主引桥伸缩缝间的碰撞效应研究还很有限。本文采用泰州长江公路大桥振动台模型试验的方法，在研究主桥纵向约束体系及行波效应[20-24]的基础上，初步研究了大跨度桥梁与引桥间碰撞问题。

1 振动台试验模型简介

1.1 试验模型

泰州长江公路大桥主缆的分跨为390 m+1 080 m+1 080 m+390 m，振动台允许的模型最大尺寸为70 m。考虑振动台面尺寸及承载能力等条件，平面几何尺寸在振动台工作范围之内，立面高度满足试验室制作场地高度要求以及模型吊装行车的高度要求，因此确定几何尺寸比例为1∶40，主要相似关系见表1。 试验模型如图1。考虑到大跨度桥梁主引桥间动力特性差异较大，地震作用下梁体容易发生碰撞。本次试验在主桥主梁与边跨梁之间安装拉压力传感器来测量碰撞力，拉压力传感器的型号是是NS-WL2型，量程5 t，碰撞力测试装置如图2。采用在钢筋表面粘贴电阻应变片测量引桥桥墩钢筋应变，采用拉线式位移计测量主引桥梁体间的相对位移。

表1 模型相似关系

图1 振动台试验模型照片Fig.1 Photo of shake table test model

(a)力传感器连接示意图

(b)力传感器连接照片图2 碰撞力测试装置Fig.2 Testing device of pounding force

1.2 试验工况

泰州长江公路大桥边塔、中塔与主梁之间都安装有横向抗风支座，限制主梁的横向位移。结合本文研究内容、试验目的、试验室振动台设备输出性能，选择两条实际地震动记录和一条人工地震动作为本次试验振动台输入地震波。选择地震动记录极可能较大范围

地涵盖了不同地震动的频谱特性，具有一定代表性，如1940 年Imperial Valley(EI Centro)代表是中等强度典型中远场地震动，《泰州长江公路大桥地震安全评价报告》提供的人工地震动加速度记录代表是桥址的场地波，1999年台湾集集地震中所记录到的TCU115( EW )波是加速度峰值都不大, 但记录持续时间都较长, 而且包含丰富的长周期成分。将上述三条地震动的地面加速度峰值调整为0.1g，并按照时间相似常数St=1/6.325进行时间轴压缩，经峰值归一化、时间轴压缩等调整后的三条地震动加速度时程曲线如图 3所示。表2中只列出相关的试验工况。

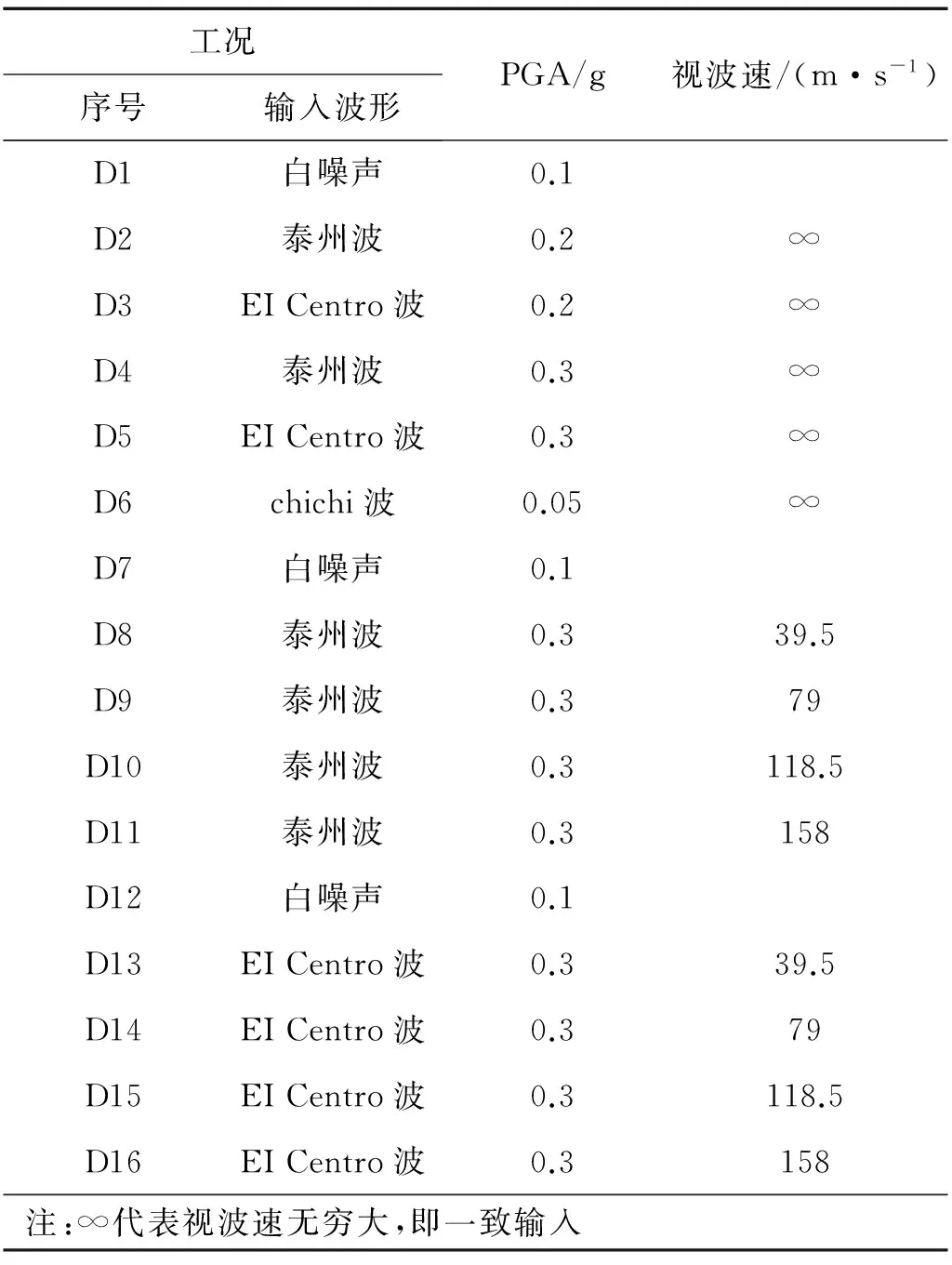
表2 碰撞效应相关试验工况

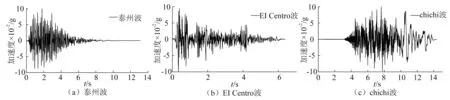
图3 试验输入地震波Fig.3 Earthquake wave used as the input motion in the tests

2 试验结果分析

主桥与引桥结构由于其动力特性存在差异, 当地震发生时将引起相邻桥跨间的不同步振动, 当桥跨间预留的间隙不能满足彼此的相对位移时就会发生相互碰撞。主桥为漂浮体系，边跨梁每幅采用两个固定支座和四个聚四氟乙烯滑板支座,初始伸缩缝间隙为3 mm。主桥纵向一阶周期为2.19 s,引桥的纵向一阶周期为0.23 s，可以看出主桥与引桥动力特性差异较大，容易发生碰撞。

选取主梁与边跨梁间的相对位移、主梁与边梁之间的碰撞力和边跨固定墩墩底测点的应变时程曲线来分析主梁与边梁间的碰撞效应。图4给出了泰州波作用下，主引桥梁体间的碰撞响应。从图4(a)可知，有碰撞与无碰撞时程曲线基本吻合，有碰撞时相对位移会减小。从图4(b)中可知，当相对位移(靠近方向运动)小于预留缝隙时会发生碰撞，碰撞6次且最大碰撞力2.34 kN。从图4(c)可知，发生碰撞时，固定墩墩底应变没有增大，反而略有减小。这是由于发生碰撞时，主桥与引桥为相互靠近运动。

图5给出了EI Centro波作用下，主引桥梁体间的碰撞响应。从图5(a)可知，有碰撞与无碰撞时程曲线基本吻合，有碰撞时相对位移会有所增加，最大相对位移(分离位移)由4.93 mm增至5.56 mm。从图5(b)中可知，当相对位移(靠近方向运动)小于预留缝隙时会发生碰撞，碰撞2次且最大碰撞力3.17 kN。从图5(c)中可知，发生碰撞时，固定墩墩底应变在碰撞点附近会有所增大。这是因为主桥追逐引桥而发生的碰撞，从而增加了引桥的碰撞响应。

图6给出了chichi波作用下，主引桥梁体间的碰撞响应。从图6(a)中可知，有碰撞与无碰撞时程曲线基本吻合，有碰撞时会引起相对位移有所增加，最大相对位移(分离位移)由6.33 mm增至7.40 mm。从图6(b)中可知，当相对位移(靠近方向运动)小于预留缝隙时会发生碰撞，碰撞2次且最大碰撞力2.13 kN。从图6(c)中可知，发生碰撞时，固定墩墩底应变在碰撞点附近会有所增大，应变值由98增至138。这是因为chichi波作用下，主桥主梁产生了较大的纵向位移，主桥追逐引桥而发生的碰撞，从而很大程度上增加了引桥的碰撞响应。

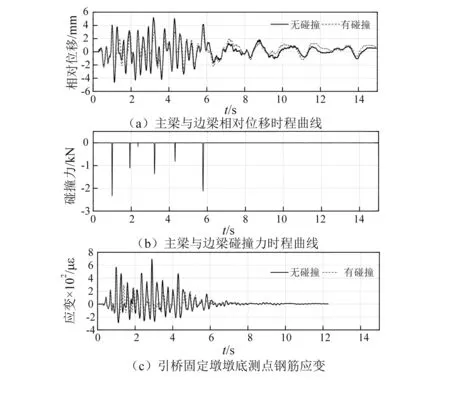
图4 泰州波作用下主引桥间碰撞响应Fig.4 Response of pounding between main bridge and approach span under taizhou wave excitation

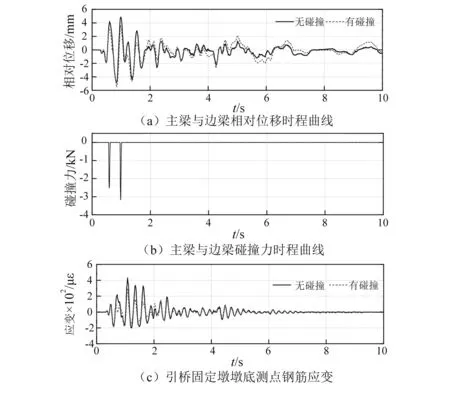
图5 EI Centro波作用下主引桥间碰撞响应Fig.5 Response of pounding between main bridge and approach span under EI Centro wave excitation

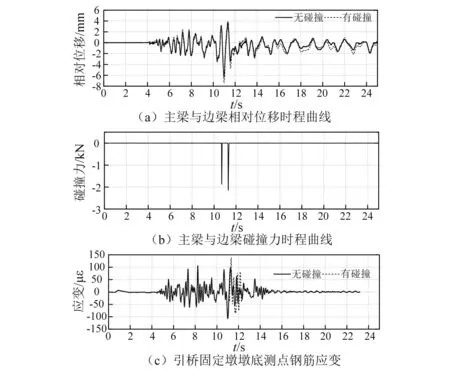
图6 chichi波作用下主引桥间碰撞响应Fig.6 Response of pounding between main bridge and approach span under chichi wave excitation

考虑行波效应时，由于主桥的地震动输入有延时，主梁与边跨梁间的相对位移波形和大小都会有所变化，从而引起不同的时刻发生碰撞。图7给出了泰州波0.3g作用下，考虑行波效应(波速39.5 m/s时)，主引桥间的碰撞响应。从图7中可知，主梁与边梁的相对位移及引桥固定墩测点的应变变化不大，而主引桥间的碰撞力最大值由2.34 kN增至3.18 kN，碰撞次数由6次减少为2次。图 8给出了考虑行波效应(波速39.5 m/s时)EI Centro波0.3g时，主梁与边跨梁间的碰撞响应结果。主梁与边梁的相对位移及引桥固定墩测点的应变变化不大，而主引桥间的碰撞力最大值由3.17 kN减小为2.11 kN，碰撞次数仍为2次。考虑行波效应时，主桥主梁位移相位发生了变化，使主引桥间的碰撞过程中，梁体接触方式(追逐或相互靠近)发生了改变。

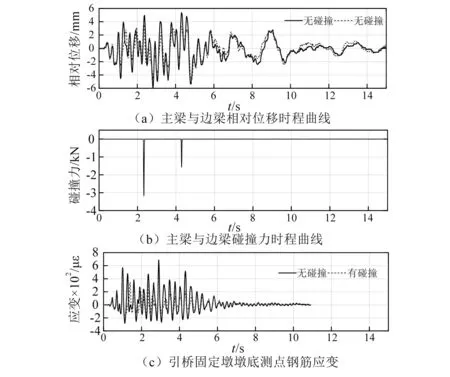
图7 泰州波(波速39.5 m/s)作用下主引桥间碰撞响应Fig.7 Response of pounding between main bridge and approach span under taizhou wave excitation (v=39.5 m/s)

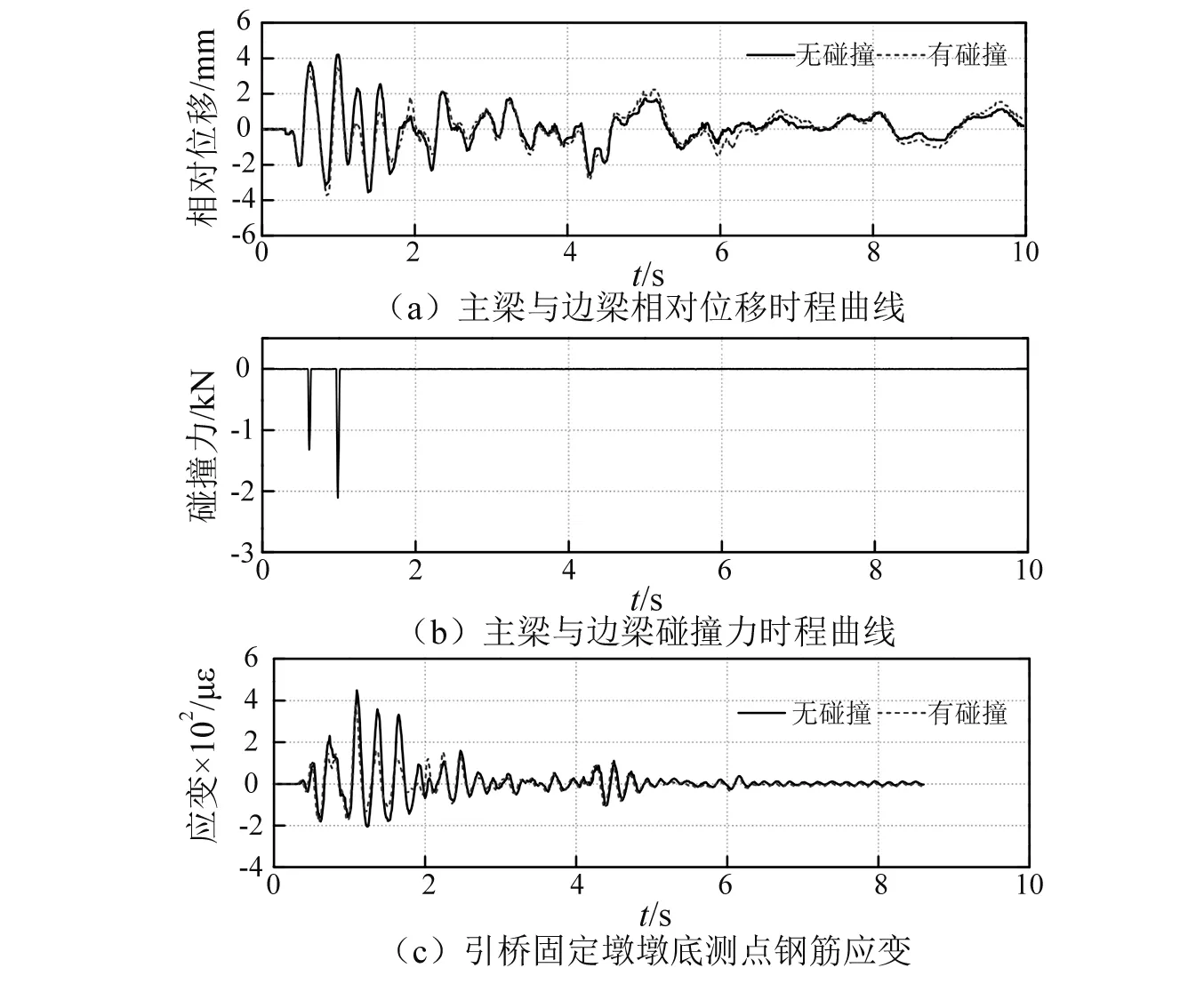
图8 EI Centro波(波速39.5 m/s)作用下主引桥间碰撞响应Fig.8 Response of pounding between main bridge and approach span under EI Centro wave excitation (v=39.5 m/s)

3 数值与试验结果对比

本文通过SAP2000 有限元程序建立振动台试验模型的结构空间动力计算模型，采用绝对位移法进行行波效应和碰撞效应数值模拟，有限元模型如图9所示。模拟碰撞效应时，首先采用线型弹簧碰撞模型，它采用线性弹簧和初始间隙来模拟相邻梁体间的碰撞，如图10所示。线性弹簧的碰撞刚度如何计算取值还不明确，通常为了防止碰撞体之间发生侵入现象，在碰撞模拟中需要设定较大的碰撞刚度，但过大的碰撞刚度不仅会带来数值计算的稳定性问题，分析结果中还会出现失真的巨大撞击力。现有的研究已表明碰撞刚度的取值对结构地震碰撞反应分析结果的影响很大，不同的取值甚至可以得到截然不同的碰撞模拟结果。在以往的研究中，众多的学者将碰撞刚度近似地取值为碰撞结构的轴向刚度。王东升等基于实测的相邻梁碰撞强震记录近似估计得到碰撞刚度取值为0.31～0.56倍的较短主梁的轴向刚度。

图9 有限元模型Fig.9 The finite element model

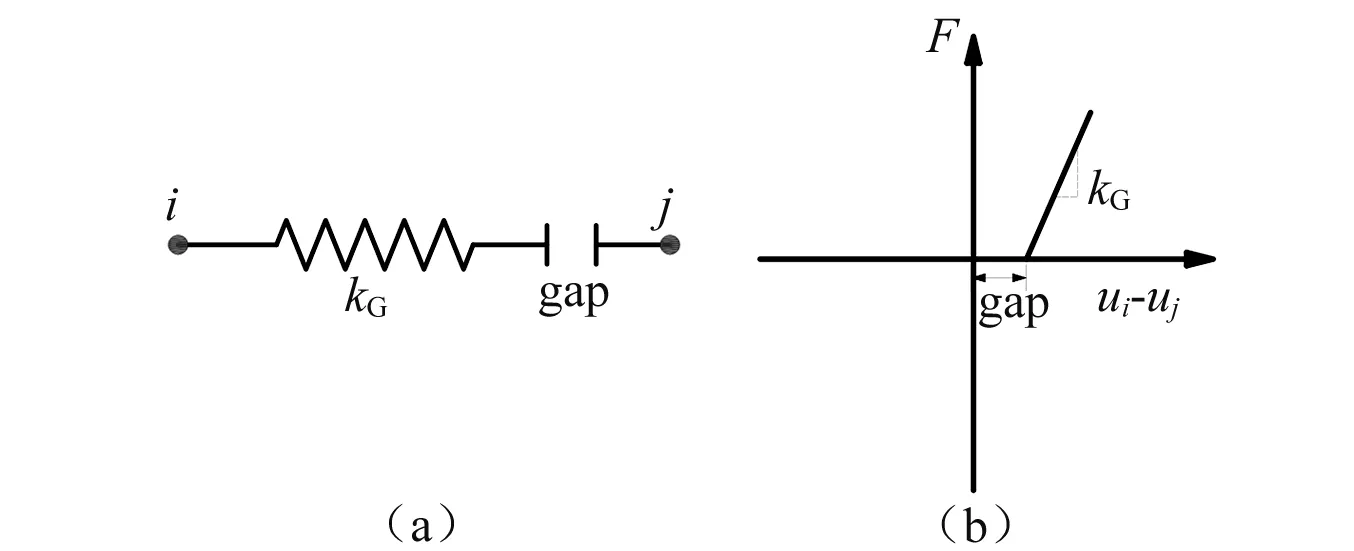
图10 线性弹簧碰撞模型及接触力关系Fig.10 Linear spring model and contact force-displacement relationship

本次试验模型边跨梁(短梁)轴向刚度EA/L为35 000 k N/m，参考以往研究成果，计算线性弹簧碰撞模型刚度取1 000 kN/m、7 000 kN/m、14 000 kN/m、35 000 kN/m做参数分析。

图11～图12分别给出了泰州波和EI Centro波0.3g输入下，主梁与边跨梁间的相对位移时程和碰撞力时程曲线。从图中可以看出，线性弹簧模型可以粗略的模拟出碰撞时主梁与边跨梁间的相对位移和碰撞力。由于线性弹簧单元不能反映碰撞过程中的能量损失，数值模拟结果与试验结果存在明显的误差。

图11 泰州波0.3g输入下主梁与边梁相对位移对比Fig.11 Comparisons of displacement history between main beam and approach span under taizhou wave 0.3g

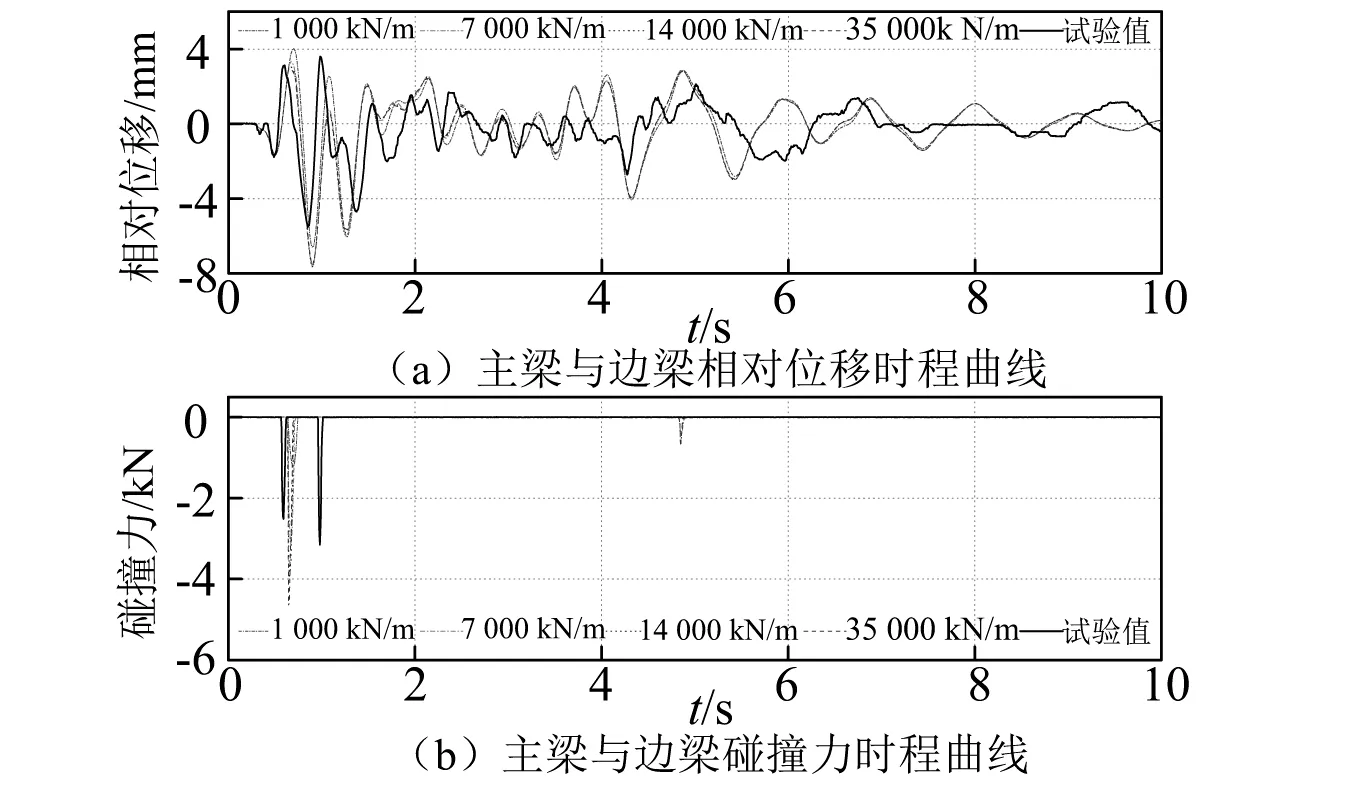
图12 EI Centro波0.3g输入下主梁与边梁相对位移对比Fig.12 Comparisons of displacement history between main beam and approach span under EI Centro wave 0.3g

目前应用广泛的另一种碰撞模型是Kelvin模型如图13所示，由线性弹簧和一个阻尼器并联组成，能够考虑碰撞过程中的能量损失。在SAP2000中可以通过三个单元组合起来实现Kelvin模型如图14所示。Kelvin单元的线性弹簧刚度为kL，gap单元的刚度为kG，kG的刚度值取约100倍的kL，这样可以保证缝闭合时kG刚度值足够大且计算结果能够收敛。由前文中参数分析结果，选择kL=7 000，c=5,kG=700 000。

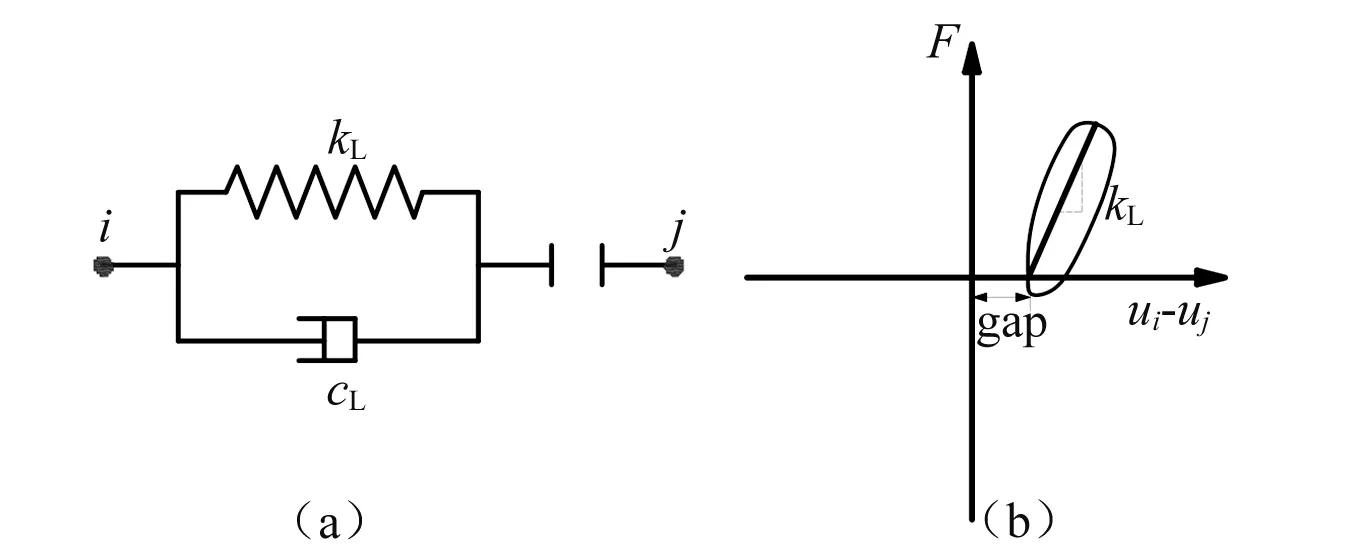
图13 Kelvin碰撞单元及接触力关系Fig.13 Kelvin element and contact force-displacement relationship

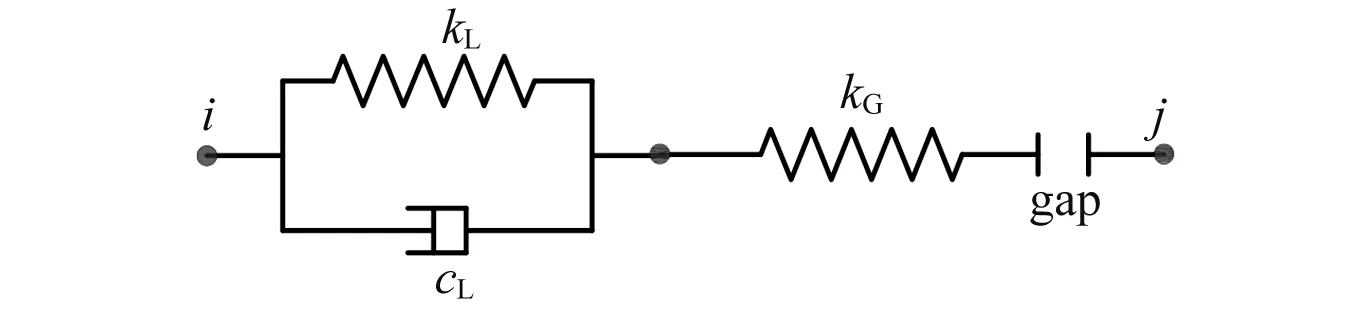
图14 Sap2000中组合Kelvin单元Fig.14 Combined Kelvin element in SAP2000

图15～16分别给出了泰州波和EI Centro波0.3g，考虑行波效应(波速39.5 m/s)输入下，采用Kelvin模型模拟的主梁与边跨梁间的相对位移时程和碰撞力时程曲线。从图中可以看出，与线性弹簧模型相比，Kelvin模型能够更好地模拟出碰撞时试验模型的碰撞效应，主梁与边跨梁间相对位移波形吻合、峰值接近，碰撞发生的次数和碰撞力大小更接近。

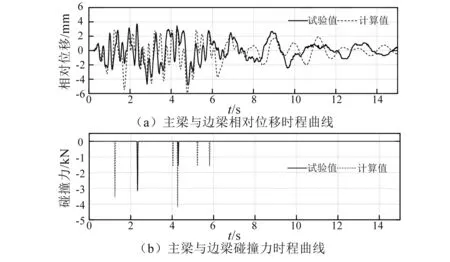
图15 泰州波0.3g(39.5 m/s)输入下主梁与边梁相对位移对比Fig.15 Comparisons of displacement history between main beam and approach span under taizhou wave 0.3g(39.5 m/s)

图16 泰州波0.3g(39.5 m/s)输入下主梁与边梁相对位移对比Fig. 16 Comparisons of displacement history between main beam and approach span under EI Centro wave 0.3g (39.5 m/s)

4 结 论

采用振动台试验在研究主桥纵向约束体系和行波效应的基础上，初步研究了三塔两跨悬索桥主引桥间的碰撞效应，分析了主引桥间发生碰撞时，主引桥梁体间相对位移、碰撞力及引桥固定墩测点的应变响应。同时分别采用线性弹簧碰撞模型和Kelvin碰撞模型对试验结果进行了数值模拟，并进行对比验证，得出以下结论:

1)振动台试验表明，主桥与引桥相互靠近运动时，其之间的碰撞会减小引桥梁位移及固定墩内力的需求；当主桥追逐引桥运动时，其之间的碰撞会增大引桥梁位移及内力的需求，增大引桥梁落梁风险。

2)分别采用线性弹簧碰撞模型和Kelvin碰撞模型对振动台试验结果进行了数值模拟。数值模拟结果表明，采用SAP2000商业软件组合Kelvin单元，接触刚度取引桥梁轴向刚度的0.2倍时，能较好的模拟试验结果。此接触刚度取值可为相似桥梁碰撞效应模拟提供试验参考。

[ 1 ] 范立础. 梁桥非线性地震反应分析-老滦河桥的震害分析[J]. 土木工程学报,1981,14(2): 41-51. FAN Lichu. Nonlinear earthquake response analysis of beam bridge-seismic damage analysis of the old Luan-river bridge[J]. Journal of Vibration and Shock, 1981,14(2): 41-51

[ 2 ] JENNINGS P C. Engineering features of the San Fernando earthquake of February 9, 1971： EERL-71-02[R]Pasadena：Earthquake Engineering Research Laboratory, California Institute of Technology, 1971.

[ 3 ] ASTANEH A, BERTERO V V, BOLT B A, et al. Preliminary report on the seismological and engineering aspects of the October 17, 1989 Santa Cruz( Loma Prieta) earthquake：UCB/EERC-89/14[R]. California：Earthquake Engineering Research Center, University of California, 1989.

[ 4 ] Earthquake Engineering Research Institute (EERI). Northridge earthquake of January 17, 1994-Reconnaissance Report, Vol 1：95-03[R]. California：[s.n.], 1995.

[ 5 ] Earthquake Engineering Research Institute (EERI). The Hyogo-Ken Nanbu Earthquake of January 17, 1995-preliminary reconnaissance report[R]. Report, No. 95-04, Oakland, CA, 1995.

[ 6 ] MAISON B F, KASAI K. Analysis for a type of structural pounding [J]. Journal of Structural Engineering, 1990, 116(4): 957-977.

[ 7 ] ANAGNOSTOPOULOS S A. Pounding of buildings in series during earthquakes [J]. Earthquake Engineering & Structural Dynamics, 1988, 16(3): 443-456.

[ 8 ] CHAU K T, WEI X X. Pounding of structures modelled as non-linear impacts of two oscillators [J]. Earthquake Engineering & Structural Dynamics, 2001, 30(5): 633-651.

[ 9 ] HUNT K H, CROSSLEY F R E. Coefficient of restitution interpreted as damping in vibroimpact [J]. Journal of Applied Mecahanics, 1975, 42(2): 440-445.

[10] ZHU P, ABE M, FUJINO Y. Evaluation of pounding countermeasures and serviceability of elevated bridges during seismic excitation using 3D modeling[J]. Earthquake Engineering & Structural Dynamics, 2004, 33(5): 591-609.

[11] 李建中, 范立础. 非规则梁桥纵向地震反应及碰撞效应[J]. 土木工程学报, 2005, 38(1): 84-90. LI Jianzhong, FAN Lichu. Longitudinal seismic response and pounding effects of girder bridges with unconventional configurations[J]. China Civil Engineering Journal, 2005,38(1):84-90.

[12] 王东升, 冯启民, 王国新. 基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J]. 工程力学, 2004, 21(2): 157-166. WANG Dongsheng, FENG Qimin, WANG Guoxin. Analysis model of pounding between adjacent bridge girders during earthquakes based on collinear impact between rods [J]. Engineering Mechanics, 2004, 21(2): 157-166.

[13] 李忠献, 岳福青, 周莉. 地震时桥梁碰撞分析的等效 Kelvin 撞击模型[J]. 工程力学, 2008, 25(4): 128-133. LI Zhongxian, YUE Fuqing, ZHOU Li. Equivalent Kelvin impact model for pounding analysis of bridges during earthquake [J]. Engineering Mechanics, 2008, 25(4): 128-133.

[14] 聂利英, 李建中, 范立础. 地震作用下结构碰撞的模型参数及其影响分析[J]. 工程力学, 2005, 22(5): 142-146. NIE Liying, LI Jianzhong, FAN Lichu. Selection of pounding analysis parameters and its effects on structure under earthquake [J]. Engineering Mechanics, 2005, 22(5): 142-146.

[15] VAN MIER J G M, PRUIJSSERS A F, REINHARDT H W, et al. Load-time response of colliding concrete bodies [J]. Journal of Structural Engineering, 1991, 117(2): 354-374.

[16] JANKOWSKI R. Experimental study on earthquake-induced pounding between structural elements made of different building materials [J]. Earthquake Engineering & Structural Dynamics, 2010, 39(3): 343-354.

[17] GUO A, LI Z, LI H, et al. Experimental and analytical study on pounding reduction of base-isolated highway bridges using MR dampers [J]. Earthquake Engineering & Structural Dynamics, 2009, 38(11): 1307-1333.

[18] 李忠献, 张勇, 岳福青. 地震作用下隔震简支梁桥碰撞反应的振动台试验[J]. 地震工程与工程振动, 2007, 27(2): 152-157. LI Zhongxian, ZHANG Yong, YUE Fuqing. Shaking table test on pounding responses of simply supported isolated bridges under earthquake excitation [J]. Earthquake Engineering and Engineering Vibration, 2007, 27(2): 152-157.

[19] HAO H, BI K, CHOUW N, et al. State-of-the-art review on seismic induced pounding response of bridge structures [J]. Journal of Earthquake and Tsunami, 2013, 7(3):132-141.

[20] LI J, YAN J,PENG T，et al. Shake table studies of seismic structural systems of a Taizhou Changjiang highway bridge model[J]. Journal of Bridge Engineering, 2015,20(3): 04014065.

[21] 闫聚考,李建中,彭天波. 泰州长江公路大桥振动台试验-试验设计及抗震体系试验结果分析[J].东南大学学报(自然科学版),2014,44(2):357-362. YAN Jukao, LI Jianzhong， PENG Tianbo. Shake table test of Taizhou Changjiang highway bridge:test design and result analysis of seismic structural system [J]. Journal of Southeast University (Natural Science), 2014, 44(2):357-362.

[22] 王军文,李建中,范立础. 非规则梁桥伸缩缝处的碰撞对地震反应的影响[J]. 土木工程学报, 2006, 30(1): 54-59. WANG Junwen, LI Jianzhong, FAN Lichu. Effect of pounding at expansion joists on seismic response of irregular girder bridges [J]. China Civil Engineering Journal,2006,30(1): 54-59.

[23] MUTHUKUMAR S, DESROCHES R. A hertz contact model with non-linear damping for pounding simulation[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(7): 811-828.

[24] 闫聚考，李建中，彭天波,等. 三塔两跨悬索桥行波效应振动台试验及数值研究[J]. 振动与冲击, 2016, 35(7): 44-48. YAN Jukao, LI Jianzhong, PENG Tianbo,et al. Shake table test and numerical analysis on wave passage effect of three-tower two-span suspension bridge [J]. Journal of Vibration and Shock, 2016, 35(7): 44-48.

Shaking table tests and numerical analysis for pounding effect between main span and approach span of long-span suspension bridges

YAN Jukao1,2， LI Jianzhong2， PENG Tianbo2， WANG Junwen3

(1. Structural Health Monitoring and Control Key Laboratory of Hebei Province,Shijiazhuang Tiedao University,Shijiazhuang 050043,China;2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 3. Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In order to study pounding effect between main span and approach span of long-span multi-tower suspension bridges, a model for 1/40 scale of Taizhou Changjiang Highway Bridge was designed, constructed and tested on a shaking table. No connections were installed between the main beam and the middle tower in the longitudinal direction. Two fixed bearings and four polysaccharide rubber sliding bearings were installed between each approach beam and piers. The initial gap distance is 3 mm at the expansion joint. Pounding responses between the main span and the approach span were tested under three earthquake waves. The shaking table tests indicated that displacements of the approach and internnal forces acting on fixed piers of the approach span decrease due to the pounding effects between the main span and the approach one when the main span and the approach one are close to each other; however, displacements of the approach span and internal forces acting on fixed piers of the approach span increase due to the pounding effects when the approach span is chased by the main span. The numerical analysis results showed that the test results can be simulated better when adopting Kelvin element combined with SAP2000 commercial software and the contact stiffness is taken as 0.2 times of the axial stiffness of the approach span. The selection of contact stiffness provided a reference for similar bridges’pounding effect simulation.

long-span suspension bridge；shaking table test；pounding effect ；traveling wave effect；contact stiffnes

973计划项目(2013CB036302)；国家自然科学基金项目(51508347)；河北省高等学校科学技术研究项目(ZD2016021)；河北省大型基础设施防灾减灾协同创新中心项目

2016-04-29 修改稿收到日期：2016-07-14

闫聚考 男，博士，讲师，1984年生 E-mail:yanjukao@163.com

U448.25

A

10.13465/j.cnki.jvs.2017.07.035