缜密思维 严谨答题
江苏省兴化市陈堡初级中学(225714) 韦海关 ●
缜密思维 严谨答题
江苏省兴化市陈堡初级中学(225714) 韦海关 ●
中考压轴题的综合性较强,不仅考查考生掌握的基础知识、基本技能、基本数学思想,还需要考生在规定时间内缜密地思维、严谨地答题、认真地书写.考生由于思维的不严密,造成失分的情况比比皆是.以下以一道中考压轴题谈谈如何缜密思维、严谨答题:
抛物线;两点间距离;一元二次方程根与系数关系;最大值;分类
一、原题呈现
(江苏省泰州市2016中考数学试题第26题)已知两个二次函数y1=x2+bx+c和y2=x2+m.对于函数y1,当x=2时,该函数取最小值.
(1)求b的值;
(2)若函数y1的图象与坐标轴只有2个不同的公共点,求这两个公共点间的距离;
(3)若函数y1、y2的图象都经过点(1,-2),过点(0,a-3)(a为实数)作x轴的平行线,与函数y1、y2的图象共有4个不同的交点,这4个交点的横坐标分别是x1、x2、x3、x4,且x1<x2<x3<x4,求x4-x3+x2-x1的最大值.
二、解法探究
(2)①如图1,如果函数y1的图象经过原点,则c=0,此时其解析式为y1=x2-4x,由抛物线的轴对称性可知它与x轴的另一公共点为(4,0),∴函数y1的图象与坐标轴的两个公共点间的距离为4.

②如图2,如果函数y1的图象不经过原点,∵函数y1的图象与y轴定有一个交点,∴函数y1的图象与x轴必只有1个公共点,∴Δ=(-4)2-4c=0,解得c=4.∴函数y1解析式为y1=x2-4x+4,设其图象与x轴交于点A,与y轴交于点B.当y1=x2-4x+4=0时,解得x1=x2= 2,∴A(2,0),OA=2;当x=0时,y1=x2-4x+4=4,∴ B函数y1的图象与坐标轴的两个公共点间的距离为.综上,函数y1的图象与坐标轴的两个公共点间的距离为4或
评注 该小题考生在答题时考虑函数y1的图象与坐标轴交点个数时,往往会因为思维的不缜密,存在漏解的情况.为了避免该情况的出现,考生在答题时要认真审题,分类讨论,严谨答题,做到会的做对、对的做全.
(3)由题意得y1中,1-4+c=-2,∴c=1,∴y1=x2-4x+1.又y2中,1+m=-2,∴m=-3,∴y2=x2-3.易求得y1、y2的顶点分别是(2,-3)、(0,-3),∴函数y1的图象可以看成是由函数y2的图象向右平移2个单位得到的.且易求得函数 y1、y2的图象的交点 E坐标为(1,-2).
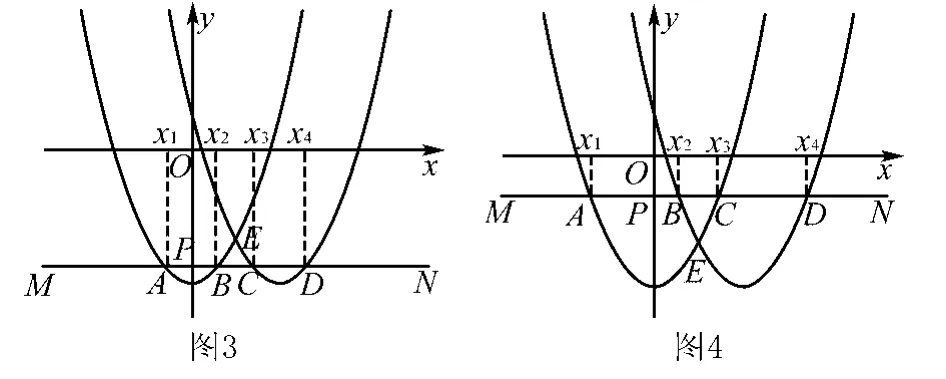
方法1:设点(0,a-3)为点P,设过点P与x轴的平行线为直线MN,设MN与函数y1、y2的图象的4个不同的交点从左到右分别是A、B、C、D.则AC=BD=2.由图3知,当MN在点E(1,-2)下方时,x4-x3+x2-x1=AB+ CD<AC+BD=4,∴此时0<x4-x3+x2-x1<4.
由图4知,当MN在点(1,-2)上方时,x4-x3+x2-x1=AB+CD=4.综上,x4-x3+x2-x1的最大值为4.
评注 将代数问题转化几为何问题,发现抛物线在同一坐标系的相互平移关系,是该法应用的精髓.但是有些考生临场答卷时,会因忽略图3情形的说明而失分.这就需要考生在答题时有较强的作图能力,并且考虑到直线MN位于点E上方、下方两种情形.
方法2:①当-3<a-3<-2,即0<a<1时,如图3,令y1=a-3,则x2-4x+1=a-3,即x2-4x-a+4=0,则令y2=a-3,则
②a-3>-2,即a>1时,如图4,令y1=a-3,则x2-4x+1=a-3,即x2-4x-a+4=0,则x4+x2=4,令y2=a-3,则x2-3=a-3,∴x2=a,则x3+x1=0,∴x4-x3+x2-x1=(x4+x2)-(x3+1)=4-0=4.
③a-3=-2,即a=1时,x2=x3,不符合题意.
综上,x4-x3+x2-x1的最大值为4.
评注 将一元二次方程根与系数关系巧妙运用到求值式中,结合合理的分类、缜密的思维,解题严谨.
G632
B
1008-0333(2017)02-0012-01

