昭示转化思想 凸显平移方法
——探究一道中考题的解法
南京金陵中学河西分校(210019) 李玉荣 ●
昭示转化思想 凸显平移方法
——探究一道中考题的解法
南京金陵中学河西分校(210019) 李玉荣 ●
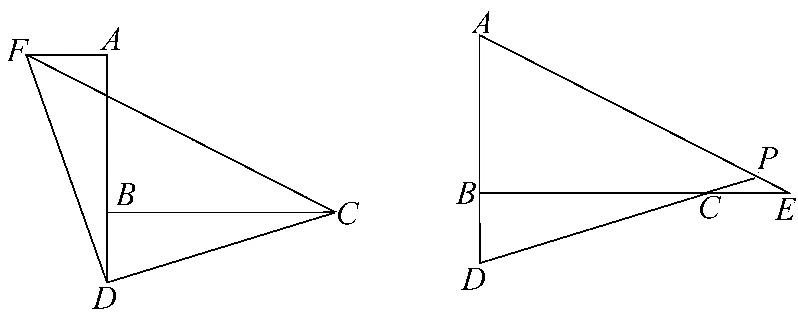
题目 如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,(1)如左图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;(2)如右图,E是直线BC上的一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
这是2015年山东省荷泽市中考数学试卷的第20题(倒数第2题),此题以常见的基本图形为载体,以“判断结论、论证结论、探究问题”的形式逐步展开,将全等三角形、等腰直角三角形的典型知识有机地结合,由浅入深、一气呵成,综合考查了学生分析问题、解决问题的能力,较好地体现了“源于基础、重在思维”的评价理念.第(1)小题是基础题,通过证明△DBC与△FAD全等,可知△CDF为等腰直角三角形;第(2)小题是一道探究性问题,考生可利用图形度量,合情推理出∠APD=45°,但怎样求出这个结果呢?
一、思转化,找到破解之门
解析 一般来说,45°角的问题与等腰直角三角形密切相关,而第(1)小题恰好得到了一个等腰直角三角形,因此,应设法将右图转化为左图,只需要“过点A作AF⊥AB,并截取 AF=BD,连接 DF、CF.”由第(1)小题知∠FCD=45°,只需证明FC∥AE,这已显而易见,从而可得∠APD=45°.
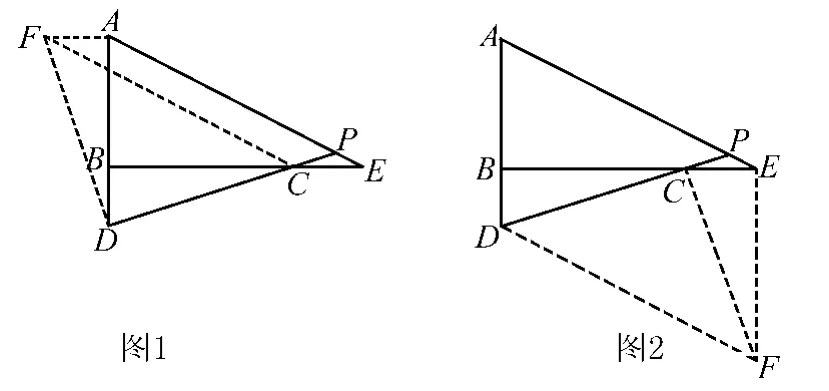
解法1 (1)略;(2)如图1,过点A作AF⊥AB,并截取AF=BD,连接DF、CF,
由(1)知∠APD=45°,AF=BD=CE,又AF∥CE,所以四边形AFEC为平行四边形,所以FC∥AE,从而∠APD =∠FCD=45°.
评析 此解法的设置体现了以人为本的原则,命题者以第(1)小题为铺垫,昭示了第(2)小题应通过转化实现目标,而“AF=CE,且AF∥CE”,等价于“将CE沿AE平移至AF”,凸显了“平移”这个重要解题方法,从平移的角度思考本题,以“AD=BC或CE=BD,”为线索,还可以探寻其它解法.
二、重平移,寻求解题它法
1.平移AD
解法2 如图2,将线段AD沿AE平移至EF,连接CF、DF,则四边形AEFD为平行四边形,Rt△BDC≌Rt△EFC,可证DC=FC,∠FCD=90°,从而∠CDF=45°,又AP∥DF,所以∠APD=∠CDF=45°.
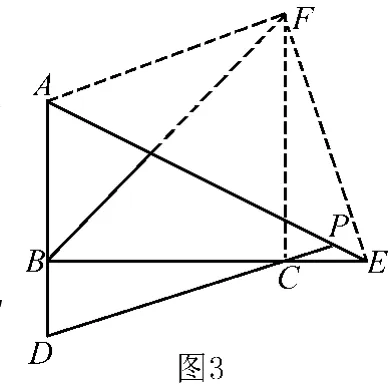
解法3 如图3,将线段AD沿DC平移至CF,连接AF、EF,则四边形AFCD为平行四边形,Rt△BDC≌Rt△CEF,可证FE=CD=FA,∠AFC=∠D,∠CFE=∠BCD,从而∠AFE=∠AFC+∠CFE=∠D+∠BCD=90°,所以∠FAE=45°,又AF∥DP,所以∠APD=∠FAE=45°.
2.平移CE
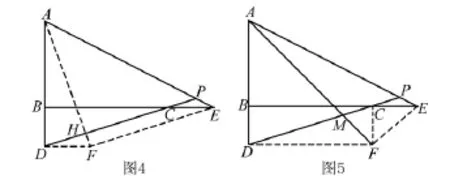
解法4 如图4,将线段CE沿CD平移至DF,连接AF、EF,则四边形CEFD为平行四边形,Rt△BDC≌Rt△DAF,可证FE∥DC,FE=DC=FA,∠BCD=∠DAF,所以∠DAF+∠ADC=∠BCD+∠ADC=90°,从而∠AHD= 90°,得AF⊥PD,所以AF⊥FE,故△AFE为等腰直角三角形,所以∠APD=∠AEF=45°.
3.平移BD(或BC)
解法5 如图5,将线段BD沿BC平移至CF,连接DF、EF,则四边形BDFC为平行四边形,△FCE为等腰直角三角形,所以,可得,从而Rt△AFE∽Rt△DFC,所以∠EAF=∠CDF,又∠AMP=∠DMF,所以∠APD=∠AFD=45°.
此题设计巧妙、变化自然,考查了学生思维的迁移能力及在解题过程中提炼方法和经验的能力,体现了命题者的独具匠心,解题者若能洞察命题者的意图,会将第(2)小题转化为第(1)小题求解,事半功倍,转化为“本”;作为教师,研究此题的解法,从中找出其规律性的东西,平移为“源”,内化为方法为教学服务、为学生所用.义务教育《数学课程标准》(2011版)明确指出:推理能力的发展应贯穿在整个数学学习过程中.推理是数学的基本思维形式,也是人们学习和生活中经常使用的思维方式,作为研究图形性质的有效方法和工具,“合情推理”与“演绎推理”相辅相成,如何在中考试题中得到有效考查,此题无疑做出了很好的诠释.我们为这样的好题点赞!
G632
B
1008-0333(2017)02-0019-01

